岭回归分析及其应用

万丽颖

(湖北大学 数学与统计学学院，湖北 武汉 430000)

岭回归分析及其应用

万丽颖

(湖北大学 数学与统计学学院，湖北 武汉 430000)

基于岭回归分析的定义及其性质，研究岭参数的存在性及其选择方法，进而得到岭参数k的选择方法有岭迹图法、方差膨胀因子法和控制残差平方和法，最后运用岭回归成功解决了现实中存在的问题，并对岭回归方法进行了推广.

多重共线性；回归系数；岭回归

岭回归分析是一种专门用于共线性数据分析的有偏估计方法，它实际上是一种改良的最小二乘法，是以放弃最小二乘的无偏性，放弃部分精确度为代价来寻求效果稍差但更符合实际的回归过程[1～3].虽然岭回归所得残差平方和比最小二乘回归要大，但它对病态数据的耐受性就远远强于最小二乘法.岭回归方法也非常灵活，它的使用存在着一定的主观人为性，但这种人为性正好是发挥定性分析与定量分析有机结合之处，在解决多重共线性问题中有着独特作用.

1 岭回归的背景

当回归方程的自变量之间出现多重共线性关系时，无法再用普通的最小二乘法对回归方程进行准确的分析, 早在 1962 年，Heer 便提出了一种改进的最小二乘估计方法，叫岭回归(ridge regression)[4]，如果自变量之间存在多重相关性，岭回归估计法是相对比较稳定的方法，而且岭回归估计的回归系数的标准差也较小.在 1970 年，Heer和 Kennard[1]给予了详细讨论.

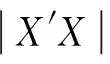
2 岭回归的定义

由于变量可能存在着量纲问题，因此这里先对数据进行标准化处理，处理过后的设计矩阵仍然用X表示，于是得到岭估计的表达式为

其中k称为岭参数.

3 岭回归的性质

证明 因为

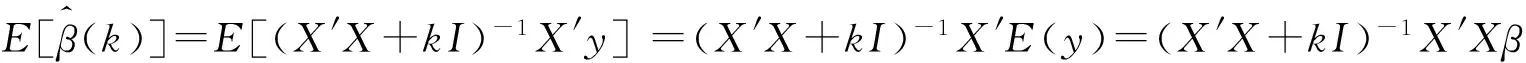
性质2 在认为岭参数k是与y无关的常数时，知

证明 由于

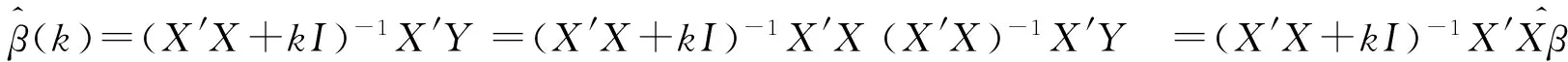
所以认为岭估计

这里‖·‖是向量的模，‖·‖等于各分量的平方和.

可以推出

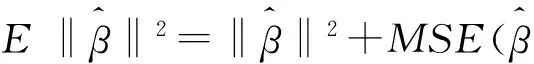
又因为

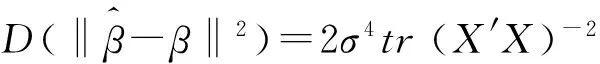
所以有

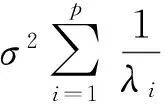
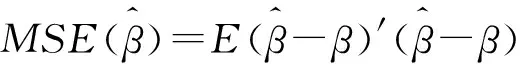
证明 设线性模型为Y=Xβ+ε,E(ε)=0,cov(ε)=σ2I，令α=Q′β,Z=XQ,这里称α为典则参数，Q为X′Y的标准正交化特征向量组成的正交矩阵的特征根，

Z′Z=Q′X′XQ=…=diag(λ1,λ2,…λn)，

其中λi(i=1,2,…,p)为X′X的特征根，模型的典则形式为

Y=Zα+ε,E(ε)=0,cov(ε)=σ2I.

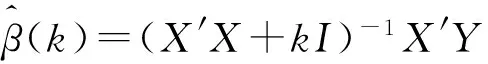
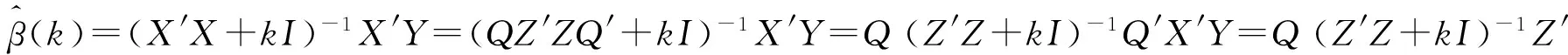
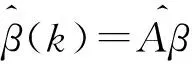
=σ2Q(Z′Z+kI)-1Z′Z(Z′Z+kI)-1Q′+Qαα′Q′+Q(Z′Z+kI)-1Z′Z(Z′Z+kI)-1Q′+Qαα′Q′+

Q(Z′Z+kI)-1Z′Zαα′Z′Z(Z′Z+kI)-1Q′-Qαα′Z′Z(Z′Z+kI)-1Q′-Q(Z′Z+kI)-1Z′Zαα′Q′，

则有

Qαα′Q′-Q(Z′Z+kI)-1Z′Zαα′(Z′Z+kI)-1Q′+Qαα′Z′Z(Z′Z+kI)-1Q′-

Q(Z′Z+kI)-1Z′Zαα′Q′

=Q(Z′Z+kI)-1[σ2(Z′Z+kI)(Z′Z)-1(Z′Z+kI)-σ2Z′Z-(Z′Z+kI)αα′(Z′Z+kI)-

Z′Zαα′Z′Z+(Z′Z+kI)αα′Z′Z+Z′Zαα′(Z′Z+kI)](Z′Z+kI)-1Q′

=Q(Z′Z+kI)-1[2kσ2I+σ2k(Z′Z)-1-k2αα′](Z′Z+kI)-1Q′

⟺2kσ2I+σ2k(Z′Z)-1-k2αα′>0

上式成立的充分条件为2kσ2I-k2αα′>0，又k>0，即有

2σ2I-k2αα′>0，

4 岭参数k的存在性及其选择

在岭参数的选择上，通常情况下人们的目的是要选择k值，此值使得均方误差达到最小，而这个k值的选择又离不开未知参数β和σ2，所以在实际问题的应用中，常常需要根据样本来确定岭参数k的值.一般地，有以下几种方法来选择岭参数k值.

4.1 岭迹图法

(1)回归方程中各回归系数的岭估计曲线变化不大，趋于平稳；

(2)回归系数基本符合实际意义；

(3)与采用最小二乘估计相比，采用岭回归方法得到估计的符号更为合理，更符合实际意义；

(4)残差平方和虽然可能有所增大，但幅度不大，并且基本趋于稳定. 岭迹图法与传统的基于残差的方法完全不同，它提供了一种全新的分析问题的思路，这是一种直观的易于理解的方法.这对于本文研究自变量之间的相互作用是有帮助的，可以说采用岭迹图法确定岭估计k值是定量分析与定性分析的一个很好的结合.但同时，岭迹图分析方法也存在着明显的缺点，比如采用岭迹图分析方法确定的岭参数k在一定程度上存在主观人为性，并且缺少可靠的理论依据.

4.2 方差膨胀因子法

通过对平均方差膨胀因子VIF的计算，可以掌握解释量之间存在多重共线性问题的严重程度[8、9].一般地，当VIF>10的时候，就认为多元回归方程的解释变量间存在着严重的多重共线性问题.

=(X′X+kI)-1X′cov(y,y)X(X′X+kI)-1=σ2(X′X+kI)-1X′X(X′X+kI)-1=σ2c(k),

其中，矩阵c(k)=(X′X+kI)-1X′X(X′X+kI)-1，这里对角线元素cjj(k)为岭估计的方差膨胀因子.

从上面的分析可以看出，当岭参数k增大时，cjj(k)减小；当k减小时，cjj(k)增大.从大量的试验中得到经验，如果应用方差膨胀因子选择岭参数k值，那么选择的k是使得所有方差膨胀因子cjj(k)≤10的k值.

4.3 控制残差平方和法

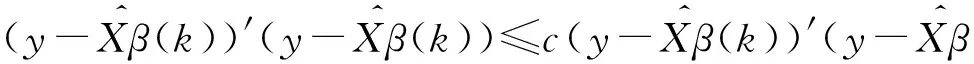
5 试验模拟

经济工作者总希望通过国内总产值x1、存储量x2、总消费量x3去预测进口总额y，为此我们收集了中国统计年鉴1949～1959年的数据[5].

由统计软件spss中的回归程序Liner-Enter可以得到系数表(见表1).

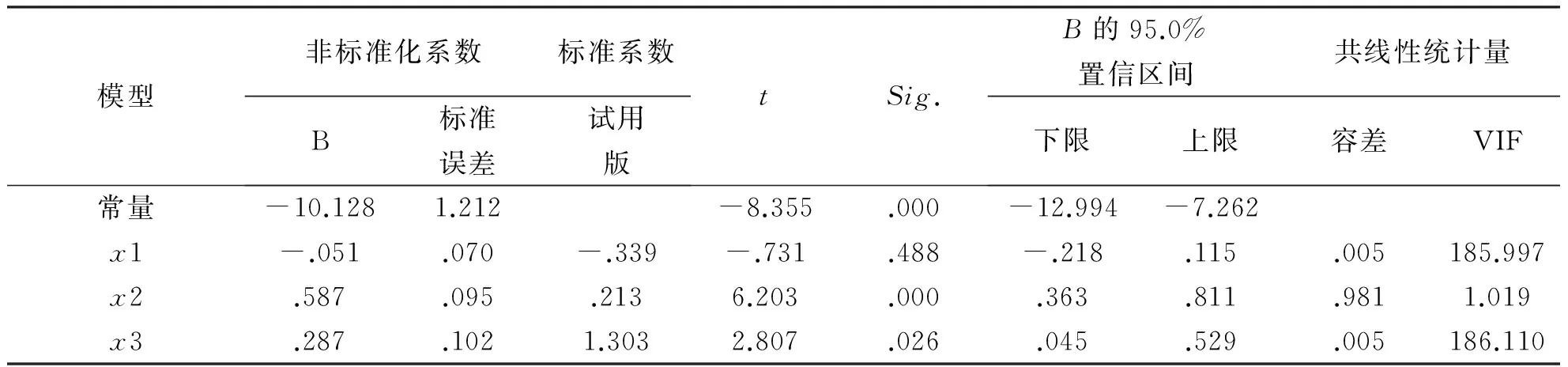
表1 系数表

由上表可见不仅x1、x3的方差膨胀因子非常大，而且β1的置信区间还包含了0点，于是其回归方程为

由上述定义来求岭估计中的参数，这里我们取岭估计中的岭参数k从0到0.1每隔0.01计算一次，由所得的数据作岭迹图，如图1所示.

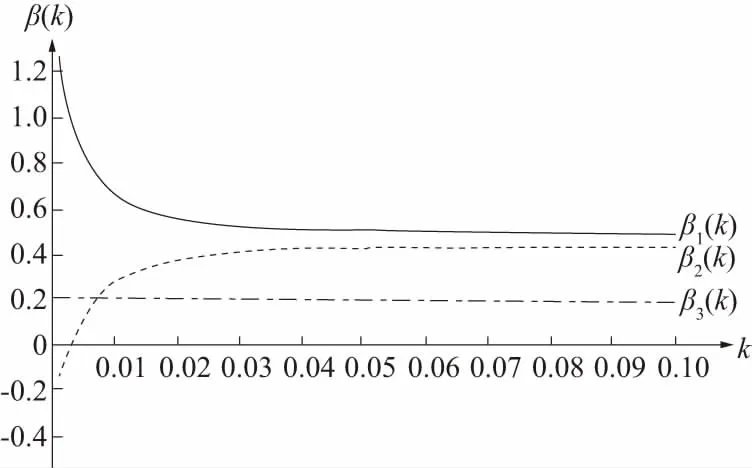
图1 岭迹图

从岭迹图上看，当k=0.04时，三条岭迹都已经比较平稳了，故可以取k=0.04建立标准化的岭回归方程为

所以岭回归方程为

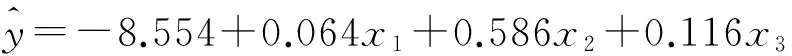
6 小结

岭回归估计已不再是无偏估计，而是通过对最小二乘法的改进，允许回归系数的有偏估计量存在而补救多重共线性的方法.采用它可以通过允许小的偏差而换取高于无偏估计量的精度，因为它接近真实值的可能性较大.岭回归方法也非常灵活，它的使用存在着一定的主观人为性，但这种人为性正好是发挥定性分析与定量分析有机结合之处，在解决多重共线性问题中有着独特作用，灵活运用岭回归方法，可以对分析各变量之间的作用和关系带来独特而有效的帮助.

[1] Hoerl A E,Kennard R W.Ridge Regression ：Biased Estimation for Nonorthogonal Problems Technometrics[J]. Technometrics ,1970, 12(6)：55-67.

[2] Yatchew A．Nonparametfic Regression Techniques in Economics[J]．Journal of Economic Literature, 1998, 6(34)：669-721．

[3] 张润楚.多元统计分析[M].北京：科学出版社，2007：18-40.

[4] 何晓群，刘文卿.应用回归分析[M].北京：中国人民大学出版社，2001：24-53.

[5] 王惠文，朱韵华．PLS回归在消除多重共线性中的作用[J].数理统计与管理，1996，15(6)：48-52.

[6] 杨 楠．岭回归在解决多重共线性问题中的独特作用[J]．统计与决策，2004(3)：14-15．

[7] 葛宏立，方陆明.无偏的岭回归迭代算法[J].数学的实践与认识，1997,27(4):320-326.

[8] 陈玲燕.多重共线性下的线性回归方法综述[J].市场研究，2008(4)：148-152.

[9] 王玉梅.多重共线性的消除：不相关法[J]．统计教育，2006，7(2)：18-19．

[10]中国国家统计局.中国统计年鉴1949～1959[EB/OL].http://www.stats.gov.cn.

责任编辑：周 伦

Analysis and Application of Ridge Regression

WAN Li-ying

(SchoolofMathematicsandStatistics,HubeiUniversity,Wuhan430000,China)

Under the definition of ridge regression, this paper has not only analyzed its qualities but also researched into existence and methods of choosing ridge parameters to obtain methods of choosing a ridge parameter K which contains ridge trace graph, variance inflation factor and residual sum of squares restricting. At last, some realistic problems have been solved by ridge regression which was spread.

multicollinearity, regression coefficient, ridge regression

2015-11-17

万丽颖(1990—)，女，河南郑州人，在读硕士研究生，研究方向：统计学及其应用.

1671-9824(2016)02-0019-05

F222.1

A