在“遗留问题”牵引下探索新知——以“三角形中位线”新授课教学为例

☉江苏省如东县丰利中学　桑圣美



在“遗留问题”牵引下探索新知——以“三角形中位线”新授课教学为例

☉江苏省如东县丰利中学桑圣美

近两年《中学数学》（下）刊发了很多关于专家教师李庾南老师课例赏析的研究文章，通过老师们对李老师课例的完整再现与跟进赏析，使得我们以读刊这种方式亲近了专家教师的课堂，收益甚大.特别在李老师诸多课例的课堂导入环节，我们注意到李老师多是以一种贴近学生最近发展区的数学现实引入新课，而少用生活现实来引入新课.这也启发我们对数学现实引入新课的思考和实践，近期笔者有机会在一次教研活动中执教“三角形中位线”一课，就选择了数学现实作为一种情境导入，也取得了较好的教学效果，本文记录这次研讨活动的过程，首先，课前对教学内容进行分析，然后，对教学流程进行概述，最后，从整体上提出三点思考，提供研讨.

一、教学内容分析

我们知道，平面图形中，三角形是最简单的，圆是最完美的.于是，平面几何中研究三角形有奠基作用.而得到三角形的性质之后，更重要的是让学生积累研究几何图形的一个范式——研究其他几何对象都可以循着这样的思路展开，同时还得到了一个“工具”，因为我们往往会利用三角形的性质去分析其他几何图形的性质.比如，以三角形的要素（三条边、三个内角）、相关要素（高、中线、角平分线、外角等）及几何量（边长、角度、面积等）之间的相互关系为基本问题，从“形状、大小和位置关系”等角度展开研究.

那么本文要探讨的三角形中位线在初中教材中多是安排在平行四边形一章之中学习，为什么在前面学习三角形时没有顺便学习呢？再往回溯源，在图形初步一章中，曾有几何习题安排学生画出任意四边形的四边中点，并度量得到的“中点四边形”四边的数量关系与位置关系，可当时只是停留在操作、度量、猜想阶段，还没有给出推理.正是基于上述认识，我们选择从七年级那个“中点四边形”的操作度量问题引入新课，将问题转化到研究三角形中位线，并成功解决中点四边形这个“遗留问题”，并进一步尝试进攻另一个“遗留问题”：三角形三边中线交于一点！整节课就在这两个难题的牵引下有序推进、展开教学.

二、教学流程概述

教学环节1.回顾“遗留问题1”，引出新知

遗留问题1：如图1，取四边形ABCD的四边中点为E、F、G、H，连接EF，FG，GH，HE.称四边形EFGH为“中点四边形”.

图1

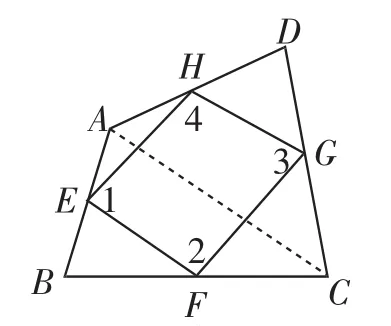
图2

通过度量“中点四边形”的四边的长，量出∠1、∠2、∠3、∠4的度数，你有什么发现？

预设意图：这是七年级上册图形初步时复习题中一道经典习题，它提示了一个奇异性质：不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形.我们已学到了平行四边形这一章，现在是不是能解决这个问题呢？（学生独立思考2分钟后，估计还是不能有效突破）

教学环节2.探究三角形中位线性质，即时运用

图3

图4

给出三角形中位线定理的文字语言、符号表达，便于学生推证.接着安排学生完成“遗留问题1”的证明，并展示学生的解答.

练习：求证：三角形的一条中位线与第三边上的中线互相平分.

预设意图：通过这个文字命题证明的练习，需要学生画图、写已知、求证.反馈学生对中位线的认识，对中位线性质定理的即时运用.

教学环节3.展现“遗留问题2”，破解难题

本课之初，我们回顾了七年级画图度量时发现的中点四边形的奇异性质，通过转化为三角形中位线性质成功解决了这个“遗留问题”，其实几何学习之路上，还有很多遗留问题，比如，三角形的三条中线交于一点，就是又一个奇异性质，我们也一直没有给出有力的证明.现在就让我们再接再厉，一起破解这个难题吧.

遗留问题2：证明三角形三条中线交于一点.

（学生独立思考2分钟后，已完成草图分析，但估计不会有进展）

预设启发：大家都证明过三角形三条角平分线交于一点吧，当时是如何证明的呢？（预设学生解答：先作两条角平分线交于一点，再证这个点也在第三条角平分线上）我们是不是也可以顺着这样思考，先作两条中线交于一点，然后设法证明第三条中线也会交于这一点呢？如图5，设△ABC的中线AD、BE交于点Q，度量一下QD、AQ的长；再度量一下EQ、BQ的长，看看它们之间有怎样的数量关系？（预设AQ=2DQ，BQ=2EQ）如何证明呢？

图5

图6

预设：根据教学经验，至少有一半的学生理解上述思路有困难，这里适当安排优秀学生复述思路，为暂时没有跟上理解的学生提供理解的时间.

讲解：我们为了证明三条中线交于一点，却舍近求远，证出了两条中线交点的一个性质，这是为什么？其实我们已很接近问题的最终解决了！如图6，同理，我们是否也能得到CQ′=2FQ′，BQ′=2EQ′.（同学们确认后）现在请同学们思考：点Q和Q′是同一个点吗？（让所有学生静静的思考，根据教学经验，不同的学生会有时差，慢慢等，安静的等，此时无声胜有声）

过渡：补全图形（如图7），现在大家都确认了Q、Q′是同一个点，我们也就解决了“重心性质定理”，即三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍.该点叫做三角形的重心.

图7

教学环节4.课堂小结与反馈练习

课堂小结：本课我们主要在解决“遗留问题”的牵引下，证明了三角形中位线，你是如何理解三角形中位线性质的？举例说说.三角形中位线与中线有何区别与联系？举例说说.

反馈练习：如图8，在△ABC中，中线BE、CD交于Q点，连接DE.

图8

（1）当BC=8cm时，DE=_____cm.

（2）当CD=9cm时，DQ=_____cm.

（3）作射线AQ交BC于点F，交DE于点M.

①线段AF是△ABC的中线吗？（直接回答“是”或“不是”）

②若BC=8cm，求DM的长.

三、教学立意的整体阐释

1.在理解数学的基础上重构教材

如上文中我们给出的教学内容分析一样，三角形中位线为什么放置在平行四边形一章学习，这是值得每个教师深入思考的，不仅是证明方法需要用到平行四边形，重要的是当中位线性质定理获证之后，之前七年级上册出现过的“遗留问题1”（中点四边形）就得到有力的解释；而三角形三边中线交于一点（重心定理）也可以得到解决，这些关联在一起的重要性质（或说奇异性质）都会因为三角形中位线性质的解决而攻克.正是基于上述认识和理解，我们决定重构教学内容，践行“用教材教”（钟启泉语），而不是“教教材”.

2.难题教学时需要教师主导启发

看了上文的课例后，也许有人会说，这是灌输式教学吧，一节课这么多难题和容量怎么可能实现呢？坦率地讲，根据我们多年的教学经验，如果让学生独立探索本文课例中提及的三角形中位线性质定理、两个“遗留问题”，可能整节课都在消耗时间，绝大多数学生一节课也不太可能探究出一个性质的证明，而教学是要追求效率的，弗赖登塔尔也说过，教师需要给学生提供“有指导”的再创造，而不是把初始问题、原生态问题抛出来，消耗学生宝贵的课堂时间.所以，本课中对于难题破解之初，一般只是安排学生2分钟左右熟悉问题背景，草图分析问题结构之后，就帮助学生讲解思路，启发推证方向，在思路贯通之后安排优秀学生复述证法路径，为理解滞后的学生赢得理解的时间.教学经验告诉我们，这样有层次地“帮助一部分人先弄懂”，再让这部分“先懂者”帮助“后懂者”是有现实意义的.

参考文献：

1.章建跃，陈向兰.数学教育之取势明道优术［J］.数学通报，2014（10）.

2.刘东升.“请你再说一遍”的功能特点探讨［J］.中学数学杂志，2014（6）.

3.乔纳森，等，主编.学习环境的理论基础［M］.上海：华东师范大学出版社，2002.

4.郑毓信.善于提问［J］.人民教育，2008（19）.

5.俞正强.种子课：一个数学特级教师的思与行［M］.北京：教育科学出版社，2013.H