一图一课，简约深刻——记“反比例函数专题复习课”的教学实录与评析

☉浙江省普陀东港中学　洪华军☉浙江省舟山第一初中　张宏政



一图一课，简约深刻——记“反比例函数专题复习课”的教学实录与评析

☉浙江省普陀东港中学洪华军
☉浙江省舟山第一初中张宏政

一、引言

2015年5月26日，张宏政名师工作室第8次教学研讨活动在普陀东港中学举行.根据导师安排，笔者为全体与会教师演绎了一节“反比例函数专题复习课”，虽自感教学中还存有不少缺憾，但整体设计及教学组织还是获得了大家的一致好评.为此，笔者把课堂教学实录整理如下，与广大同仁分享，也欢迎诸位同仁批评指正.

二、教学实录

1.提供图像线索，梳理相关知识

问题1：如图1，根据图像，你能得到什么信息？

师：还有吗？

生2：双曲线关于原点成中心对称，且关于直线y=x和直线y=-x成轴对称；图像虽无限接近于坐标轴，但与坐标轴永不相交.

图1

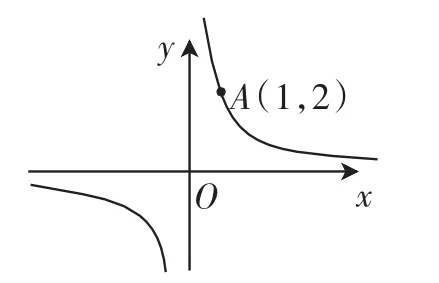
图2

师：看来，同学们对反比例函数的性质都理解得不错，若这条双曲线经过点A（1，2）（如图2），你还能得出哪些信息？

生众：可求出k=2.

（学生独立完成，小组交流讨论后派组内成员上台展示）

生3（指着屏幕上的图像解释道）：当x≥1时，0＜y≤2，当y<2时，x＜0或x＞1.

点评：从一道开放性的图像问题入手，进一步赋予具体的数值，既有效梳理了反比例函数的相关知识，也凸显了函数研究的重要方法——数形结合思想.问题2中对图像信息的读取既是学生的易错点，也是后面环节中用图像法解决不等式问题的关键，这里洪老师通过小组合作、学生互助、自主解决问题的方式进行，既充分贯彻面向了全体的教学原则，也充分奠定了学生的后续学习基础.

2.突出本质特征，强化基本方法

问题3：作直线AO交另一支曲线于点B（如图3），你又能得出什么结论？请简述你的理由.

生4：点B（-1，-2），因为双曲线是中心对称图形，因此，A、B两点关于原点成中心对称，所以点B（-1，-2）.

生5：可求出直线AB的解析式为y=2x.

图3

图4

生6：可以求出点C和点D的坐标.

师：怎么求呢？

师：唔，很不错.在此基础上，你们还可以得到哪些结论？

师：通过本题的解决，我们可以看到，方程、不等式与函数之间存在内在的联系.从图像上看，方程组的解所对应的有序数对就是函数的交点坐标；不等式的解就是函数的部分图像所对应的x的值.因此，方程组、不等式问题除了用代数法解决，还可以用图像法来解决.

点评：本环节一是突出图像上点的坐标与函数解析式之间的数形转化关系，二是旨在强化方程、不等式的图像解法，有了前面问题2的铺垫，学生能比较顺利地解决此问题，从而使数形结合思想潜移默化地根植于学生内心，也为今后二次函数的学习打下坚实的基础.

3.代数几何一体，方法能力共生

问题4：如图5，过点A、C作直线，分别交y轴、x轴于点I、J，这样你们又能得到些什么结论呢？

生8：可以求点I、J的坐标.

师：如何求？

生8：先求直线AC的解析式，求出来是y=-x+3，再把x=0、y=0分别代入，求出I的坐标为（0，3），J的坐标为（3，0）.

师：非常不错.进一步还能求什么？

师：刚才这位同学求△AOC的面积时遇到了一点小麻烦，现在我们都来帮他算一算.每个同学独立完成后，请与组内成员先交流，看看方法是否一致，各学习组长整理下不同的解题方法后，请各小组派代表发言.

（约8分钟后，各组代表分别上台呈现了下列方法）

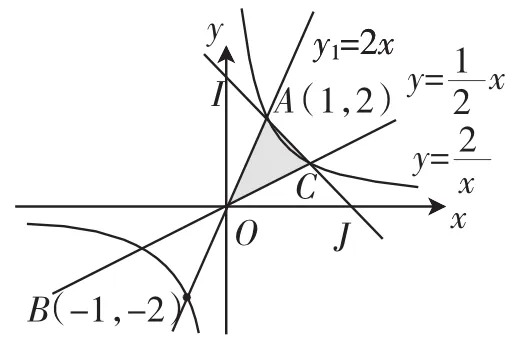
图5

图6

解法2：如图6，分别过点A、C作AE⊥x轴于E，CF⊥x轴于F.

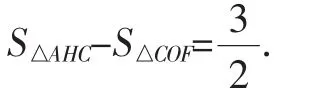
图7

图8

图9

师：同学们都表现得非常好，给出了这么多的解法.那么请大家观察一下这些方法，它们之间有没有什么共性？

生10：我发现这些方法其实用的都是割补法，只不过割补的方式有所不同.

师：这位同学观察的非常到位，大家再来看看这些割补的方式，又有什么共性吗？

生11：我发现除了第一种方法用的是两个现成的三角形的面积之差，其余四种方法添的辅助线要么平行于x轴，要么平行于y轴.

师：嗯，观察的非常仔细.因为坐标系中平行于x轴或y轴的线段的长度比较容易用坐标来表示，这样利用平行于两坐标轴的直线割补出来的图形的面积相对而言也比较容易求.所以化斜为直进行割补是我们解决坐标系中几何问题的一般思路.好了，既然已知反比例函数的解析式能求一些图形的面积，那么，若已知图形的面积，是否倒过来能求反比例函数的比例系数k呢？让我们再看下面的问题.

几分钟后，巡视发现绝大多数学生还没有解题方向.于是提醒道：既然要求k的值，那么能否用含k的代数式建立一个等量关系？请思考图中哪些图形的面积与k有关，哪个图形的面积又容易用两种不同的方法表示？

（一语惊醒梦中人，经过3分钟左右的思考后）

生12：连接OH.

由HC=CF，得S△OFH=2S△DCF=k.

则S矩形OFHG=2S△OFH=2k.

则k+8=2k，故k=8.

变式1：如图10，若矩形OFHG中，HC=nCF，四边形AOCH的面积为8，求k的值.

图10

图11

（学生陷入了沉思中，几分钟后）

生14：老师，设点A（a，b），再过A、C作x轴的垂线，垂足分别为E、F，则OE=a，AE=b，再过C作CL⊥AE于L，则△ALC≌△CFJ，这样EF=FJ，若OE=EF的话就好了，但我证不出来.

师：为你深入的思考点赞.但你既然设了点A的坐标，为什么不先试试用含a、b的代数式来表示点C的坐标呢？

师：还有不同的想法吗？比如，能否就本图与图10之间进行适当的联系？

（这时下课铃声却在不经意中响起了，给本课留下了一丝遗憾）

点评：这一阶段着力围绕解析式↔点的坐标↔图形面积的相互转化关系而展开，既巩固了前面的学习成果，又有机渗透了割补法、化斜为直、构建方程模型等重要的数学策略及基本方法.其中围绕k的几何意义，着力变式拓展，方法提炼，从中有效提高了学生分析问题、解决问题的能力.值得一提的是，教学中洪老师总是能留给学生充分的思考和交流的时空，以便让学生能在操作中思考，思考中感悟，感悟中归纳，虽然课堂看上去不那么完整，留下了少许遗憾，但却体现了常态课堂的不可预见性.

三、评析

本堂复习课，突出了本工作室一直倡导并努力践行的“自然、简约、大气”的教学设计思路，以一题一课的形式展开，课堂气氛活，思维含量足，方法落实佳，让学生在探索中领悟方法，在过程中寻求发展，亦取得了较理想的复习效果.

1.一图贯之，简约自然

众所周知，复习课的教学既要帮助学生梳理基础知识，建立知识联系，形成认知网络；更要帮助学生深入体验数学思想方法，感悟数学基本经验，进而有效提升学生的思维能力.而要实现这些目标，就必须设计结构良好的问题系列进行有效驱动.纵观本课的设计，洪老师以数形结合这个研究函数的重要工具为主要认知线索，以读图识图为基本手段，以求解图形面积的方法研究为重要载体，以k的几何意义的认识深化为拓展内容，用1个图形和5个衔接紧密的问题进行有效串联，由浅入深，层层深入，自然生成本课的全部内容.既符合学生的认知心理，兼顾了不同层次学生的不同复习要求；也使得学生有相对充裕的时间对问题进行深入探讨，让思维在交流中得以增值，方法在比较中得以优化，数学本质在思考中得以凸显，有效达成预期的教学目标.

2.着力方法，重视能力

数学复习课中的核心认知活动应是在知识的回顾、组织与运用中，概括、提炼思想方法与解决问题的策略，进而发展学生的思维能力.本课的教学对此的呈现令人印象深刻.一是在设计上，通过设置开放性问题，既利于全体学生积极参与，获得不同视角下的多样化结论，也便于学生通过对这些结论的梳理，全面掌握获取图像信息的方法.又如让学生体验方程、不等式、函数之间的内在联系，既是学生函数学习过程中的重点，也是难点.这里洪老师先用反比例函数上定义域与值域的对应关系搭建脚手架，再过渡到两个函数之间的大小比较，于是便生成了生7的精彩回答，有效突破了难点.二是在教学策略上，如围绕学生提出的△AOC的面积计算时遇到的困境，没有让个别优生直接展示思路了事，而是在分组深入研究后，从多样化的解题思路的比较中归纳共性，提炼方法，这样在学生积极体验后再渗透化斜为直的数学解题策略，就取得了较好的教学效果.三是在启发思考上，如学生在解决问题5一筹莫展时，洪老师通过提出元认知的问题给学生提供了一般化的思考策略，从而激活了学生的思维链条，使学生对运用方程模型思想解决问题也有了更深刻的认知.

3.生为中心，突出自主

整堂课，洪老师按照基于学情、适度发展的原则，较好体现了“学为中心，生为主体”的教学理念.如上课伊始，先用低起点的开放性问题唤醒学生的学习心向，在满足学生成功的学习体验的同时，也营造了积极的学习氛围.当部分学生解决问题存在困难时，洪老师没有急于求成，以讲代学，而是采用先独立学习，后小组交流的方式来互帮互学，分享智慧，使合作学习真正落到实处.当多数学生思考遇到困境时，则以启发引领帮助学生摆脱困境.当学生呈现自己一些不成熟的思路时，洪老师也没有急于否定学生的想法，而是顺着学生的想法给予恰当的点拨，从而生成了与预设不同的解法.虽然为此导致没有完成预设的问题关联分析，也没有进行课堂小结，但却真实反映了常态的课堂场景，突出了学生的学习自主性.

当然从弥补缺憾、改进教学的角度思考，或许对教学可以作如下优化.（1）去掉图1，直接呈现图2并提出问题1.这样学生获取图像信息会更直观具体，起点也更低些.（2）删去问题5中的变式1，概因这个变式与原题方法一致，但涉及解含参数的方程，课标对此不作要求.这样就可以节省出一些宝贵的教学时间.另外，在呈现问题5之前，若先引入一个已知面积求k值的简单问题进行铺垫，学生对问题5的解决可能更顺畅，也利于学生对变式2进行分析与解决.

参考文献：

1.张宏政，郑伟君.凸显函数认知线索，有效提升思维能力——一堂二次函数复习课的教学实录与评析［J］.中学数学教学参考（中），2010（1-2）.

2.张宏政，史美华.初中数学课堂中高效教学行为的特征分析——基于一堂数学课的观察与诊断［J］.中学数学教学参考（中），2012（3）.

3.陈建新，张宏政.让数学探究活动更真实——记“反比例函数的图像与性质（1）”的教学实践与评析［J］.中学数学（下），2014（1）.