基于过程教育的“矩形（第1课时）”课例及分析

☉浙江省宁波市华茂外国语学校　顾谦勇



基于过程教育的“矩形（第1课时）”课例及分析

☉浙江省宁波市华茂外国语学校顾谦勇

一、背景介绍

《义务教育数学课程标准（2011年版）》（以下简称“课标（2011年版）”）倡导过程教育，以全面发挥数学的育人功能.但在以浙教版义务教育教科书数学八年级下册第五章第1节“矩形（第1课时）”为载体的“多人同课异构”式的教研活动中发现，课堂教学普遍与过程教育存在偏差，也没有体现以学为中心的思想.网上查阅同类课例发现也有类似现象.鉴于此，笔者在重复式观课与反思的基础上，对这节课的教学进行重建，改进后的教学过程与效果得到了同仁的认可.现将其整理出来，以飨读者.

二、教学实录

环节1：经历回顾并提出问题的过程——明确研究的问题

师：我们在研究三角形时，根据三角形的形状、大小是千变万化的这一特点，除了研究三角形的概念、性质与判定，还研究了三角形的特例以加深对三角形的认识.由于平行四边形的形状、大小也是千变万化的，所以除了研究平行四边形的概念、性质与判定，也要研究平行四边形的特例以加深对平行四边形的认识.

师：三角形有哪些情况比较特殊？

生1：等腰三角形、等边三角形、直角三角形、等腰直角三角形.

师：不错.其实，三角形还有许多情况比较特殊，只是这些三角形研究意义不大——其现实情景与性质不多，而等腰三角形、直角三角形有丰富的现实情景与性质.

师：类似地，平行四边形有哪些有价值的特例呢？本节就来探讨这个问题.（揭示课题）

环节2：参与定义矩形的活动——形成矩形的概念

师：现在请大家依次完成下列任务.

（1）画图：画一个邻边长分别为1和2的平行四边形.

（2）讨论：①这样的平行四边形可以画几个？②在这些平行四边形中，有没有面积最大的？为什么？③这个面积最大的平行四边形的内角有什么特点？

（约3分钟后）

师：这样的平行四边形可以画几个？

生2：这样的平行四边形可以画无数个.

师：好的.在这无数个平行四边形中，有没有面积最大的？为什么？

生3：有面积最大的.因为平行四边形在变化的过程中，其高有最大值.

师：有道理.这个面积最大的平行四边形的内角有什么特点？

生4：这个面积最大的平行四边形的内角是直角.

师：好的.一般地，如图1，我们把有一个角是直角的平行四边形叫做矩形.例如，小学里学过的长方形和正方形都是矩形.

图1

师：矩形有丰富的生活情景.能举几个矩形的生活实例吗？

生5：书本、黑板、电视机屏幕的表面等都是矩形的形象.

生6：电脑键盘上的小方块、魔方、骰子的表面等也都是矩形的形象.

师：不错.生活中为何经常采用矩形的结构？

生7：矩形的结构具有工整、美观、设计方便的特点.

生8：采用矩形的结构能使通风面积最大.

生9：矩形具有对称性，能给人一种美的感觉.

师：有道理.美观与面积最大是生活中采用矩形结构的主要理由.

师：矩形与平行四边形是怎样的关系？

生10：矩形是特殊的平行四边形.

师：好的.矩形与线段是怎样的关系？

生11：矩形可以看成是由给定条件的四条线段按一定的规则拼接出来的.

生12：矩形可以看成是由给定条件的两条线段按一定的规则平移得到的.

师：不错.矩形与直角三角形是怎样的关系？

生13：矩形可以分成两个全等的直角三角形.

生14：两个全等的直角三角形可以拼成一个矩形.

生15：矩形可以看成是直角三角形通过中心对称得到的.

师：好的.矩形与生活中的矩形是怎样的关系？

生16：矩形可以看成是从矩形形状的物体中抽象出来的.

师：不错.由此可见，产生矩形有多种方式.

师：因为矩形是平行四边形，所以矩形具有平行四边形的所有性质，而矩形又是特殊的平行四边形，像特殊三角形有特殊性质一样，矩形还有哪些特殊的性质？

师（稍停顿后）：请大家先画一个合适的矩形，再用适当的方法从矩形的边、角、对角线等角度进行探索.（允许小组合作）

师（约2分钟后）：谁来说说探索的方法与结果？

生17：我用观察的方法得到：四个角都是直角；两条对角线相等.

生18：我用测量的方法得到：四个角都是直角；两条对角线相等.

生19：我用推理的方法得到：四个角都是直角；两条对角线相等.

师：好的.大家用不同的探索方法得到了相同的结果.由此可以形成怎样的猜想？

记得上四年级的时候，爸妈嫌我精力太旺盛，就给我报了个国标舞班。刚学的时候每天练功，两条腿上各放2公斤的哑铃或者砖头，一开始还能拼命撑，撑个半小时已经是极限了，就开始慢慢往下滑，直到腿酸得嗷嗷直叫，一屁股坐地上。

生20：矩形的四个角都是直角；矩形的两条对角线相等.

师：好的.猜想得到的结果不一定正确，需要用推理的方法来证明.

师：根据矩形的定义和平行四边形的性质，容易证明“矩形的四个角都是直角”.怎样证明“矩形的两条对角线相等”？请大家先依次完成下列任务.

（1）根据题意画出图形；

（2）在图形上标注已知条件；

（3）结合图形写出已知与求证.

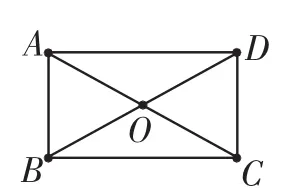
图2

师（待学生完成任务）：如图2，要证AC=BD，只要证什么？

生21：只要证△ABC≌△DCB.

师：好的.要证△ABC≌△DCB，只要证什么？

生21：只要证AB=DC，∠ABC=∠DCB.

师：好的.能证AB=DC、∠ABC=∠DCB吗？

生21：能证.因为矩形的对边相等，矩形的四个角都是直角.

师：好的.请大家按证明的格式把证明过程完整地写出来.

师（待学生完成任务）：这样矩形有以下的性质.

定理1：矩形的四个角都是直角.

定理2：矩形的两条对角线相等.

师：获得矩形的性质经历了哪几个步骤？

生22：画图→观察、测量、推理→猜想→证明→表达.

师：不错.探索矩形的性质的策略是什么？用的是什么方法？

生23：策略是分类讨论和从特殊到一般归纳，用的方法是观察、测量或推理.

师：好的.证明定理2经历了哪几个步骤？

生24：画图→标注→写已知与求证→分析→证明.

师：好的.这些数学活动的经验以后会经常用到.

师：因为平行四边形是中心对称图形，所以矩形也是中心对称图形.矩形是不是轴对称图形？为什么？

生25：矩形是轴对称图形.例如，如图2，过矩形对角线的交点O作AD的垂线，因为OA=OD，OB=OC，所以垂线必定垂直平分AD与BC，所以矩形ABCD是轴对称图形.由此可得，矩形是轴对称图形.

师：好的.你运用了从个别到普遍的思想.矩形有几条对称轴？

生26：矩形有两条对称轴.

生27：若矩形是正方形，则它有四条对称轴.

师：非常好！这样关于矩形还有以下的结论.

矩形既是中心对称图形，又是轴对称图形，它至少有两条对称轴.

师：从图2还能发现什么？

生28：它有四个直角三角形.

生29：矩形两条对角线把矩形分成四个面积相等的等腰三角形.

生30：相对的两个等腰三角形全等.

生31：用矩形的性质可以证明“直角三角形斜边上的中线等于斜边的一半”.

师：非常好！这些结论在以后计算与证明的过程中会经常用到.

环节4：参与尝试知识应用的活动——合作解答有代表性的问题

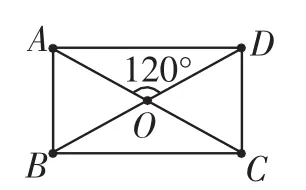
图3

师：现在请大家解答下列问题.

已知：如图3，矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AB=4cm.问：

（1）△AOB是怎样形状的三角形？

（2）矩形对角线的长是多少？

师（约1分钟后）：谁来回答（1）？

师：好的.谁来回答（2）？

生33：△AOB是等边三角形且AB=4cm，所以OB=AB=4cm，所以AC=BD=2OB=8cm.

师：好的.这个矩形的面积是多少？

师：好的.若∠AOD=90°，则对角线的长是多少？

师：好的.解题后对给定问题作进一步探索是研究数学的基本经验.

（接下来，要求学生完成课本中的练习题，并在学生完成任务后进行交互反馈与评价）

环节5：参与回顾与思考的活动——合作进行反思与总结

首先，教师出示下列“问题清单”，并要求学生围绕“问题清单”进行回顾与思考.（1）本节课研究了哪些内容？我们是怎样研究的？（2）产生矩形有哪几种方式？矩形的本质特征是什么？

（3）矩形有哪些性质？获得矩形的性质经历了哪几个步骤？

（4）证明矩形的性质经历了哪几个步骤？你对矩形有何感触？

其次，教师组织学生交互反馈，同时教师边倾听、边评价.

第三，在此基础上，教师总结本节课的研究内容、研究方法及研究意义.

三、教学分析

矩形可以看成是从生活中抽象出来的，也可以看成是数学自身逻辑的产物.尽管产生矩形有多种方式，但采用演绎方式能体现教材意图和类比思想.矩形的数学本质是其内角是直角，其研究内容主要是组成要素之间的关系，其知识“生长点”是长方形与正方形的概念、平行四边形的知识等.矩形是平面几何的重要研究对象，它与线段、三角形、平行四边形等有密切关系；矩形的性质是基础知识，它在几何计算与证明中会经常用到；研究矩形概念采用的从一般到特殊的策略及从特殊到特殊和从特殊到一般的方法，研究矩形性质采用的分类讨论的策略及从特殊到一般的方法，对后继学习有指导作用.获得矩形概念的过程和蕴含的从特殊到特殊与从特殊到一般思想，认识矩形与相近概念之间的关系和生活中为何经常采用矩形结构的过程，探索与证明矩形性质的过程和蕴含的从特殊到一般思想及研究几何图形性质的数学活动经验，用矩形性质解决具体问题的过程和蕴含的演绎思想等，这些对发展学生的智力、能力、个性有积极作用.但“课标（2011年版）”对“矩形”提出的教学要求是“理解矩形概念及其与相近概念之间的关系，探索并证明矩形的性质定理”.目前在这节课的教学中普遍存在的问题是：（1）经历回顾并提出问题的过程缺失，而是直接创设画图情境或实验情境，总给人有知识从天而降的感觉；（2）获得概念之后反思矩形与相近概念之间关系的过程缺失，导致学生对矩形概念达不到理解的程度；（3）探索并证明矩形性质的过程不规范——没有引导学生经历必要的思维站点，导致不能满足学生感悟思想和积累经验的需要.本课例根据“课标（2011年版）”提出的教学要求和教材的意图，将其教学立意于“类比、感悟、积累、发展”，并以教材提供的题材为载体，从学生已有的知识与经验出发，运用演绎和分类的思维策略、从特殊到特殊和从特殊到一般的思维方法及教师价值引导与学生自主建构相结合的适度开放的方式，引导学生经历完整的认知过程.在“回顾并提出问题”的教学中，既有回顾研究三角形思维结构的过程，又有通过类比提出问题的过程，以揭示新旧知识之间的内在联系和激发学生的学习兴趣.在“定义矩形”的教学中，既有“画图、推理、定义”的过程，以形成矩形的概念，又有获得概念之后的反思，以认识矩形与相近概念之间的关系.在“探索矩形的性质”的教学中，既有“画图、定向探索、猜想、证明”的过程，以形成矩形的性质，又有获得性质之后的反思，以感悟其蕴含的研究几何命题的数学活动经验和揭示矩形的其他性质.在“尝试知识应用”的教学中，既有学生自主实践与思考的过程，又有交互反馈与评价的过程，以巩固知识和发展智慧技能，还有解决问题后的变式与拓展，以感悟研究数学的基本经验.在“回顾与思考”的教学中，既有教师价值引导下学生的思考与交流，又有教师的总结性讲解.这体现了过程教育和以学为中心的思想，也遵循了导入性教学、概念教学和图形性质教学的基本规范，能全面发挥其育人功能.

由此可得，对从上位概念中演绎出来的概念的教学，要引导学生经历演绎的过程（从一般到特殊演绎或从特殊到特殊演绎），要有思维与思想的内化过程；对图形性质的教学，要引导学生经历“探索→猜想→分析→证明→表达→反思”的过程.这样能使学生在高情意学习氛围中，理解和掌握数学的知识与技能，体会和运用数学的思想与方法，积累数学活动的经验，发展能力和形成敢想、敢说、敢于创新的良好个性.

参考文献：

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.范良火.义务教育教科书·数学（八年级下册）［M］.杭州：浙江教育出版社，2013.