升降速过程中转子系统油膜失稳规律*

马 辉， 王雪玲， 牛和强， 李 辉

(东北大学机械工程与自动化学院 沈阳，110819)

升降速过程中转子系统油膜失稳规律*

马 辉， 王雪玲， 牛和强， 李 辉

(东北大学机械工程与自动化学院 沈阳，110819)

以某悬臂转子-轴承系统为研究对象，基于有限元方法建立了转子-轴承系统动力学模型。通过时域图、三维谱图和幅频响应图得到了转子系统升降速过程中出现的油膜失稳特征，分析了不同角加速度值在升降速过程中对1阶和2阶油膜失稳规律的影响。研究发现：升降速过程中产生的切向惯性力会改变油膜失稳转速，与稳态情况(角加速度为零)相比，升降速情况下2阶油膜失稳转速有所延迟；升速过程中随着角加速度值的增大2阶油膜失稳转速略有增加、降速过程略有减小；降速过程与升速过程相比，出现明显的迟滞效应。

升降速; 转子-轴承系统； 滑动轴承； 油膜振荡； 有限元

引 言

随着旋转机械向高转速、大跨度和柔性轻结构方向发展，滑动轴承油膜与转子相互作用引起的油膜失稳问题日益突出。高速旋转机械高阶油膜失稳的研究对于旋转机械设计以及应用具有重要意义。

在滑动轴承的非线性油膜力模型的研究方面，Muszynska等[1]提出了一个基于流体圆周平均流速的非线性油膜力模型，基于实验验证了此模型能够预测转子-密封系统的失稳问题。基于“无限短”轴承的假设，Capone[2-3]提出了动态油膜力模型，计算结果表明具有良好的精度和收敛性。刘长利等[4]在Capone油膜力的基础上，对裂纹和油膜耦合故障转子周期运动分岔做了分析。以上两种模型忽略了非稳态项对油膜边界的影响，Zhang等[5]提出一种非稳态油膜力模型，研究了转子偏心对系统失稳的影响，并与稳态油膜力模型进行了对比，结果显示非稳态油膜力模型更接近工程实际。张彦梅等[6]指出非稳态油膜力模型可能更适用于大扰动的非线性转子动力学研究，并与稳态油膜力模型进行对比分析。

在滑动轴承导致的油膜失稳研究方面，Ma等[7]研究了双盘转子系统不同相位角在稳态情况下对于2阶油膜失稳的影响。Wan等[8]研究了多盘转子系统联轴器不对中转子系统的非线性动力特性，研究发现不对中可以延迟油膜振荡的发生，降低振荡幅值。EI-Shafei等[9]建立了一个悬臂柔性转子系统，通过实验分别研究了不同不平衡量、油压及不对中条件对转子系统失稳的影响。

旋转机械的升降速过程中需要引入角加速度的惯性效应。de Castro等[10]建立一个中心圆盘的不平衡水平和垂直转子系统，引入角加速度因素，在短轴承假设的基础上研究了转子系统在升降速过程的动态特性。Jing等[11]基于连续质量模型研究了转子-轴承系统的动态特性及转子系统的升降速过程中出现的迟滞效应。

可见，国内外学者对转子系统的升降速过程进行了系统研究，但对于在升降速过程中角加速度对2阶油膜失稳影响关注较少。笔者以文献[9]的悬臂转子-轴承系统为研究对象，在建模中引入角加速度影响因素，采用Newmark-β数值积分法，分析了角加速度在悬臂转子-轴承系统升降速过程中对油膜失稳转速的影响及系统复杂非线性动力学特性。

1 有限元模型及模型验证

为了更好地模拟分析转子系统模型的动力学特性，根据以下假设对系统进行简化：a.转轴采用Timoshenko梁进行模拟,盘模型以集中质量叠加到对应的节点上;b.左、右滑动轴承均采用文献[5]的非线性非稳态油膜力模型来模拟[5]。

轴段单元有限元模型如图1所示。其中：x,y以及θx,θy分别为横向位移和旋转方向的角位移；下标A和B分别为节点A和B。转轴的梁单元位移向量ue表示为

(1)

其中:上标e表示每个有限元单元;每个梁单元的质量、刚度和陀螺矩阵分别表示为Me,Ke和Ge(详见文献[12])。

图1 轴段单元有限元模型Fig.1 The finite element model of the shaft element

该转子-轴承系统运动方程为

(2)

(3)

其中：M为质量矩阵；G为陀螺矩阵；C为阻尼矩阵；K为刚度矩阵；q为位移向量；Fu，Fb和Fg分别为转盘产生的激振力及升降速的惯性力、轴承油膜力和重力外激励向量；θ为系统的转角。

笔者采用瑞利阻尼来描述系统阻尼，表达式为

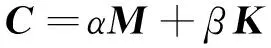
(4)

(5a)

(5b)

其中：ωn1和ωn2分别为系统的1阶和2阶固有角频率(r/min)；ξ1和ξ2分别为系统的1阶和2阶模态阻尼比。

基于短轴承理论，张文等[5]提出的非稳态油膜力模型为

(6)

(7)

其中：η为润滑油黏度；L，D和c分别为滑动轴承长度、直径和平均直径间隙；无量纲油膜力fbx和fby的表达式详见文献[5]。

为了验证仿真计算的有效性，选用文献[10]中相同的模型参数，取降速的角加速度值为3 πrad/s2，仿真结果与文献结果对比如图2所示。可以看出，仿真模型1阶油膜失稳频率为21.82 Hz，油膜失稳转速为2 203.8 r/min，这些仿真结果和文献中的实验结果(22 Hz和2 160 r/min)基本一致，可见本研究数值仿真方法的有效性。

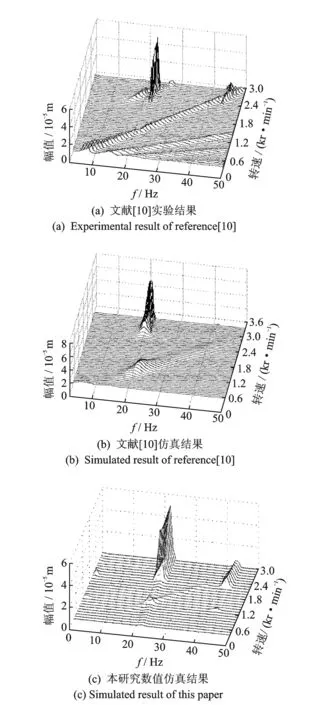
图2 本研究仿真结果和文献[10]实验结果、仿真结果三维谱图对比Fig.2 The spectrum cascades comparison among the simulation results of this paper, the simulation and experiment results of reference [10]

2 角加速度对油膜失稳影响

2.1 悬臂转子系统有限元模型建立

文献[9]中的悬臂转子-轴承系统结构尺寸如图3所示。4个盘的结构及质量相同，其他仿真参数如表1所示。当悬臂转子系统左右轴承均采用弹簧阻尼模型，支撑刚度和阻尼分别取k=2×108N/m，c=2×103N·s/m时，通过计算得到该悬臂转子系统的1阶和2阶临界转速分别为1 637.37 r/min和4 112.74 r/min，与文献[9]中提到的1阶和2阶临界转速(1 680 r/min和4 171 r/min)的实验结果相近。

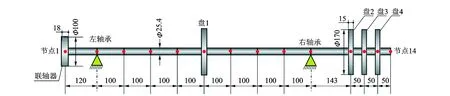
图3 悬臂转子-轴承系统结构尺寸、节点及单元示意图(单位：mm)Fig.3 Schematic of the overhung rotor-bearing system, nodes and elements(unit:mm)

Tab.1 Model simulation parameters of the rotor-bearing system

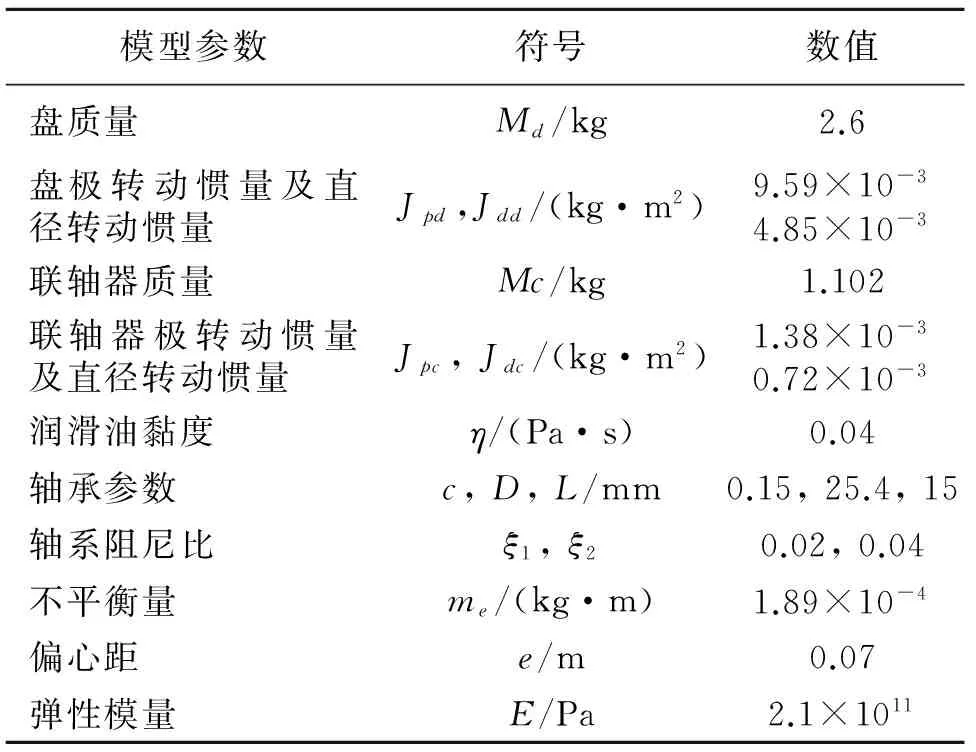
模型参数符号数值盘质量Md/kg2.6盘极转动惯量及直径转动惯量Jpd,Jdd/(kg·m2)9.59×10-34.85×10-3联轴器质量Mc/kg1.102联轴器极转动惯量及直径转动惯量Jpc,Jdc/(kg·m2)1.38×10-30.72×10-3润滑油黏度η/(Pa·s)0.04轴承参数c,D,L/mm0.15,25.4,15轴系阻尼比ξ1,ξ20.02,0.04不平衡量me/(kg·m)1.89×10-4偏心距e/m0.07弹性模量E/Pa2.1×1011

2.2 数值计算及理论分析

假定仅在盘1存在偏心。升降速过程的匀角加速度α范围为25～125 rad/s2，取值间隔为25 rad/s2。通过分析稳态和升降速的三维谱图(限于篇幅，仅给出角加速度值为0，25和125 rad/s2情况下的三维谱图)，分析5种角加速度值在升降速过程中的1阶和2阶油膜失稳转速，得到不同角加速度值下的1阶和2阶油膜失稳转速规律曲线，如图4所示。图中，P1和P2两点为稳态情况下1阶和2阶油膜失稳转速(见图5)，其值分别为3 625 r/min和8 125 r/min。

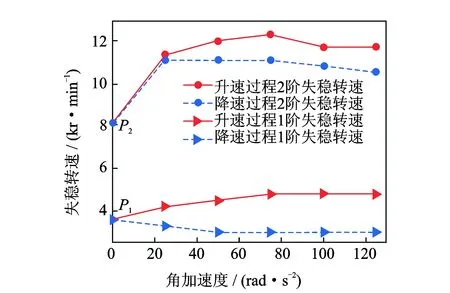
图4 油膜失稳转速-角加速度规律曲线Fig.4 The oil film unstable thresholds curve with different angular accelerations

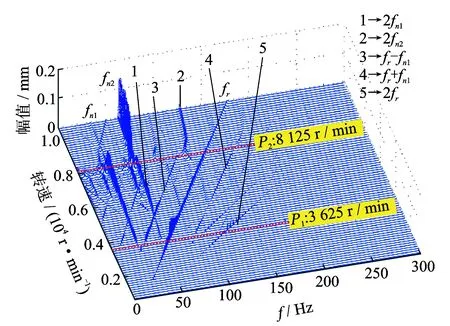
图5 右轴承竖直方向稳态响应三维谱图(α=0)Fig.5 The spectrum cascade of vertical stable responses of the right bearing (α=0)

从图4可以看出，在升速过程中，当角加速度增加时，1阶油膜失稳转速较稳态油膜失稳转速不断向后推移并趋于平稳。当α∈(25,75) rad/s2时，2阶油膜失稳比例有增大的趋势；当α∈(75,125) rad/s2时，2阶失稳比例有减小的趋势。降速过程中出现明显的涡动现象，1阶油膜失稳转速较稳态有所提前，并且明显滞后于升速过程，即出现了迟滞效应。当α∈(25,125) rad/s2时，2阶油膜失稳转速在10 810±300 r/min范围变化，趋势较为平稳。

不同角加速度情况下的三维谱图如图6所示。由图可知，在升降速过程中出现的频率成分包括1阶油膜振荡频率fn1、2阶油膜振荡频率fn2和转频fr，及组合频率成分2fn2，fr-2fn2，fr-fn1和fr+fn1等。当角加速度α=25 rad/s2时，升速过程中1阶和2阶油膜失稳转速分别为4 206 r/min 和11 410 r/min；降速过程中对应值分别为3 306 r/min和11 110 r/min。当角加速度α=125 rad/s2时，升速过程中1阶和2阶油膜失稳转速分别为4 806 r/min 和11 710 r/min；降速过程中对应值分别为3 006 r/min和10 510 r/min。

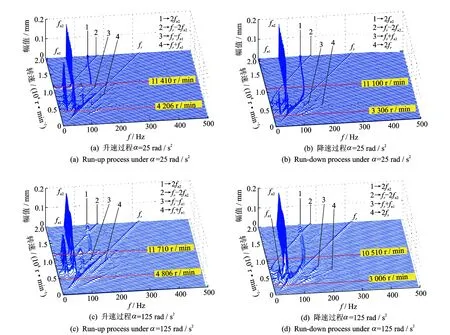
图6 右轴承竖直方向升降速响应三维谱图Fig.6 The spectrum cascades of vertical responses of the right bearing during the run-up and run-down processes

做角加速度值为25，125 rad/s2右轴承处升降速过程时域波形如图7所示。从时域图看出，由于惯性效应的存在，在滞后于1阶和2阶固有频率处有明显的共振峰，并且角加速度值为125 rad/s2的共振时间明显短于角加速度值为25 rad/s2的时间。

右轴承处升降速过程的幅频响应曲线如图8所示。通过对比发现，整体看降速过程的油膜失稳转速和升速过程的油膜失稳转速有明显迟滞特性，即油膜失稳转速并没有在升速过程出现失稳位置消失，而是降速到更低的转速时失稳现象才消失。

油膜对轴颈的总压力在垂直于偏心距方向存在一个导致油膜失稳的切向分力[13]。升降速过程中的1阶和2阶油膜失稳转速与稳态油膜稳转速产生差异的原因可能是由于在升降速过程中产生的切向惯性力，影响了油膜的失稳规律。

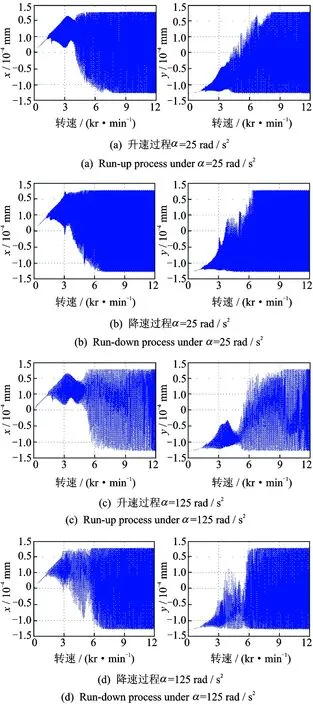
图7 右轴承水平和竖直方向升降速位移时域波形Fig.7 The time-domain displacement waveforms of the right bearing in horizontal and vertical directions

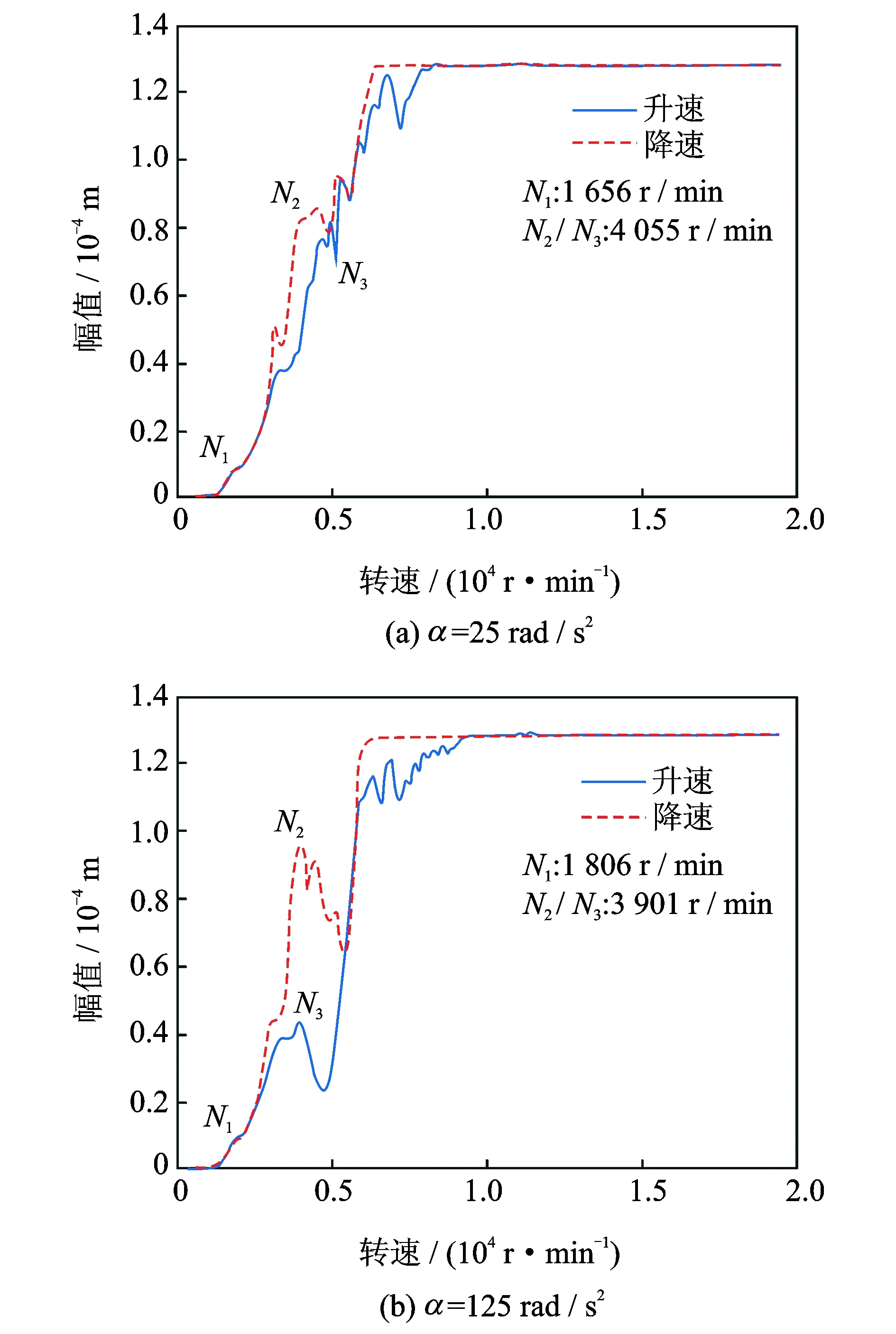
图8 升降速幅频响应曲线Fig.8 The amplitude-frequency responses of rotor system during the run-up and run-down processes

3 结 论

1) 升速过程和稳态情况相比，系统的1阶和2阶油膜失稳转速有所推迟。在笔者研究的角加速度范围内，油膜失稳转速随着角加速度值的增大而增加并趋于平稳，并且2阶的油膜失稳转速变化幅度大于1阶。

2)降速过程中，由于惯性效应的存在，系统的1阶油膜失稳转速较稳态有所提前，2阶油膜失稳转速较稳态有所推迟，失稳时间延长。此外，降速过程相对于升速过程而言，1阶和2阶油膜失稳并没有在转速降低到升速过程中出现失稳的转速位置消失，而是降低到更低的转速失稳才消失，即出现了迟滞效应。

[1] Muszynska A, Bently D E. Anti-swirl arrangements prevent rotor/seal instability[J]. Journal of Vibration Acoustics Stress and Reliability in Design, 1989,111:156-161.

[2] Capone G. Orbital motions of rigid symmetric rotor supported on journal bearings[J]. La Meccanica Italiana, 1986,199(199):37-46.

[3] Capone G. Analytical description of fluid-dynamic force field in cylindrical journal bearing[J]. L′Energia Elettrica, 1991,3(3):105-110.

[4] 刘长利,夏春明,郑建荣,等.裂纹和油膜耦合故障转子周期运动分岔分析[J].振动、测试与诊断,2008,28(1):35-38.

Liu Changli, Xia Chunming, Zheng Jianrong, et al. Study on bifurcation of periodic motion of rotor system with crack and oil whirl fault[J]. Journal of Vibration, Measurement & Diagnosis, 2008,28(1):35-38. (in Chinese)

[5] Zhang Wen, Xu Xiaofeng. Modeling of nonlinear oil-film force acting on a journal with unsteady motion and nonlinear instability analysis under the model[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2000,1(3):179-186.

[6] 张彦梅, 陆启韶.一种非稳态油膜力模型下转子系统的碰摩分岔分析[J].振动工程学报,2002,15(1):68-73.

Zhang Yanmei, Lu Qishao. Impact bifurcate analysis on a bearing-rotor system with unsteady oil film forces[J]. Journal of Vibration Engineering, 2002,15(1):68-73. (in Chinese)

[7] Ma Hui, Li Hui, Zhao Xueyan, et al. Effects of eccentric phase difference between two discs on oil-film instability in a rotor-bearing system[J]. Mechanical Systems and Signal Processing, 2013,41(1):526-545.

[8] Wan Zhao, Jing Jianping, Meng Guang, et al. Theoretical and experimental study on the dynamic response of multi-disk rotor system with flexible coupling misalignment[J]. Journal of Mechanical Engineering Science, 2012,226:2874-2886.

[9] El-Shafei A, Tawfick S H, Raafat M S, et al. Some experiments on oil whirl and oil whip[J]. Journal of Engineering for Gas Turbines and Power, 2007, 129(1):144-153.

[10]de Castro H F, Cavalca K L, Nordmann R. Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model[J]. Journal of Sound and Vibration, 2008,317(1):273-293.

[11]Jing Jianping, Meng Guang, Sun Yi, et al. On the oil-whipping of a rotor-bearing system by a continuum model[J]. Applied Mathematical Modelling, 2005,29(5):461-475.

[12]Ma Hui, Yang Jian, Song Rongze, et al. Effects of tip relief on vibration responses of a geared rotor system[J]. Journal of Mechanical Engineering Science, 2014,228(7):1132-1154.

[13]钟一谔,何衍宗,壬正，等.转子动力学[M].北京:清华大学出版社，1987:63-68.

航空发动机振动监测和分析系统研制成功

森德格公司(sendig.com.cn)，经过多年的研究和大量现场试验，在近期成功发布了系列化航空发动机振动监测和分析仪器产品。包括有：SAVT-1H小型手持式振动测量仪器，可测量发动机的多种通频振值；SAVT-2H航空发动机振动分析仪和动平衡仪，可测量多种振值、波形、频谱。同时配有设备状态监测及趋势分析软件和故障诊断专家系统，可以自动生成各种报告；SAVT-5航空发动机振动变送器，是为连续监测发动机振动值的在线监测仪表，可以在驾驶舱实时显示振值，并在振值超标时立即报警以避免重大事故的发生。

SAVT系列仪器已经过生产厂家台架和外场实机的多次成功考验，填补了我国飞行器发动机振动监测和分析仪器缺少自主知识产权产品的空白。

10.16450/j.cnki.issn.1004-6801.2016.01.009

��人才支持计划资助项目(NCET-11-0078)

2014-01-10；修回日期：2014-03-04

TH113.1

马辉，男，1978年9月生，博士、副教授。主要研究方向为旋转机械动力学与故障诊断领域的理论与技术应用。曾发表《Effects of eccentric phase difference between two discs on oil-film instability in a rotor-bearing system》(《Mechanical Systems and Signal Processing》2013，Vol.41,No.1-2)等论文。 E-mail：huima@me．neu．edu．cn