基于CSLBP的轴承信号时频特征提取方法*

2016-04-13张云强张培林吴定海

振动、测试与诊断 2016年1期

关键词：二值中心对称时频

张云强，张培林，吴定海，李兵

(军械工程学院车辆与电气工程系石家庄，050003)

基于CSLBP的轴承信号时频特征提取方法*

张云强，张培林，吴定海，李兵

(军械工程学院车辆与电气工程系石家庄，050003)

针对滚动球轴承振动加速度信号特征提取问题，提出一种基于中心对称局部二值模式(center-symmetric local binary pattern，简称CSLBP)的时频特征提取方法。首先，利用广义S变换对滚动球轴承振动加速度信号进行处理，通过采用时频聚集性度量准则自适应地确定广义S变换的调整参数，从而获取时频分辨性较好的二维时频图；然后，计算二维时频图的CSLBP，提取CSLBP纹理谱描述滚动球轴承振动加速度信号的时频特征。对滚动球轴承正常、外圈故障、内圈故障和滚动体故障4种不同状态的振动加速度信号进行了研究。结果表明，CSLBP纹理谱能有效地表达滚动球轴承振动加速度信号的时频特征，与局部二值模式(local binary pattern,简称LBP)和统一模式LBP纹理谱相比，CSLBP纹理谱具有特征维数低和区分性能好的优点。

滚动球轴承；时频分析；特征提取；中心对称局部二值模式；广义S变换

引言

滚动球轴承是机械设备中常见的旋转部件之一。当滚动球轴承发生故障时，其振动加速度信号是一种典型的非线性、非平稳信号。时频分析能将一维时域信号变换到二维时频域内，全面揭示信号不同频率成分的时变特性，是分析非平稳信号的有力工具[1-3]。然而，二维时频图的维数巨大，不能直接作为轴承信号的特征参数。为降低存储空间和后续轴承信号分类的复杂度，必须对时频图作进一步特征提取[4]。

局部二值模式和统一模式局部二值模式通过对局部图像进行对比度补偿，可有效描述图像的局部结构特征，在图像纹理检索和分类中取得了较好的效果[5-8]。然而，LBP和统一模式LBP刻画的纹理过于精细且模式数量较多，不利于图像特征描述和分类。在LBP的基础上，Heikkilä等[9]提出了中心对称局部二值模式。CSLBP在大幅度降低模式数目的同时，提高了图像特征描述能力[10-11]。

时频图本质上是一种特殊的图像，同样具有明显的纹理特征。鉴于此，笔者引入中心对称局部二值模式，提出一种基于中心对称局部二值模式的轴承信号时频特征提取方法。由于广义S变换[12-13]具有比短时傅里叶变换、连续小波变换和S变换等传统时频分析技术更好的时频分辨性能，因此在提取滚动球轴承特征时，采用广义S变换对轴承振动加速度信号进行处理，从而获取信号的二维时频图。提取时频图的CSLBP纹理谱作为轴承信号的特征参数，通过对4种不同状态的滚动球轴承振动加速度信号进行特征提取和分类，验证了CSLBP纹理谱用于表达轴承时频特征的可行性和有效性。

1 广义S变换

广义S变换是对S变换的推广，具有更好的时频聚集性。对于一维时间信号x(t)，广义S变换的定义[13]为

(1)

其中：w(t)为高斯窗函数。

w(t)表达式为

(2)

由式(2)可知，广义S变换高斯窗函数的标准差为频率f的p次方的倒数，即σ=1/|f|p，其中，p为调整参数，通常取值在0～1之间。因此，广义S变换的窗宽随着频率的增大而减小，在低频具有较高的频率分辨率，在高频具有较高的时间分辨率。由于参数p的存在，广义S变换在分析非平稳信号时具有更强灵活性。理论上，通过时频聚集性度量准则对参数p进行合理取值，广义S变换可以获得最优的时频分辨性能。

2 中心对称局部二值模式

2.1 局部二值模式

LBP的基本思想是，根据图像局部区域的中心像素灰度值与邻域像素灰度值的差异进行二进制编码，从而刻画图像的局部纹理特征[14]。基本LBP定义在3×3的矩形邻域，其编码规则如图1所示。当邻域像素的灰度值fi≥fc时，对应位置编码为1，否则编码为零，然后按顺时针方向读出8位二进制数，即为该邻域中心像素的LBP。

由于基本LBP处理的邻域是一个大小固定、形状固定的矩形，应用于某些场合存在明显不足，Ojala等将3×3的矩形邻域扩展到了任意半径和任意邻域点数的圆形邻域。图2为3种常用的圆形邻域，其中，P=8，R=1的圆形邻域与3×3矩形邻域等价。邻域半径为R、点数为P的LBP计算方法[15]如式(3)和式(4)所示。

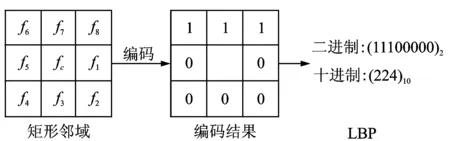
图1 LBP编码规则Fig.1 The code rule of LBP

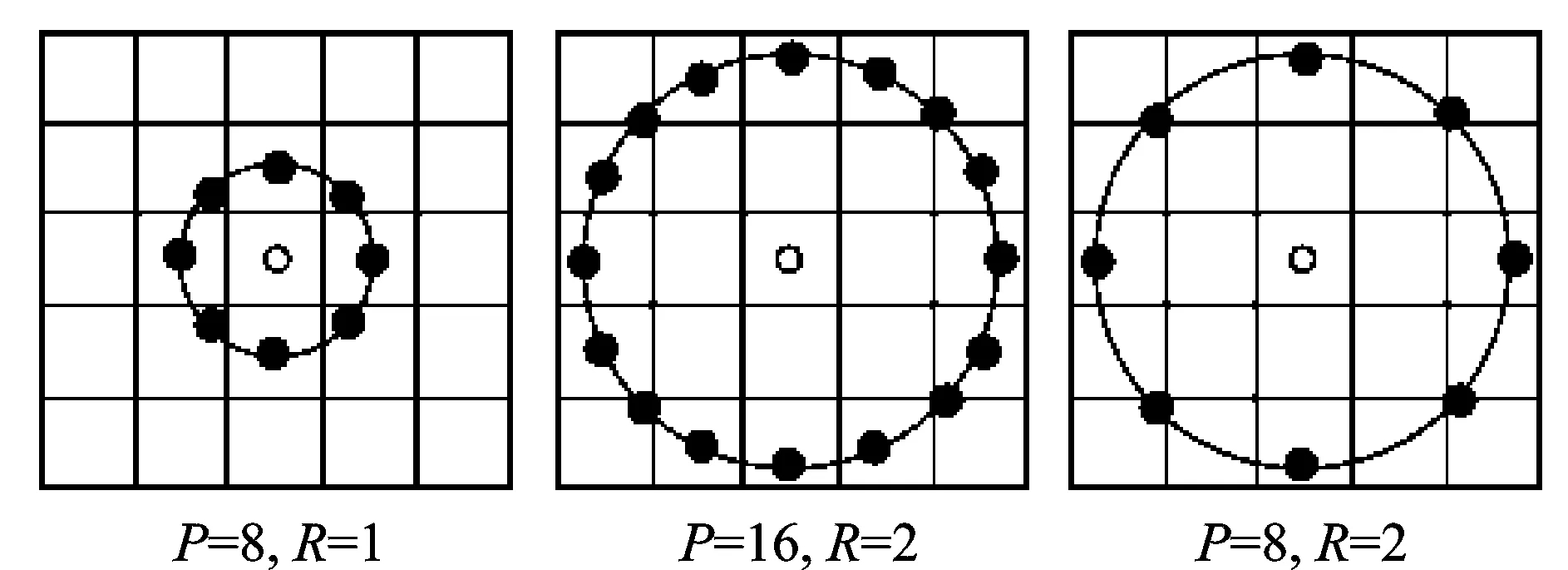
图2 常见的圆形邻域Fig.2 The common circular neighborhoods

(3)

(4)

其中：P为邻域点数，在基本LBP中P=8。

2.2 中心对称局部二值模式

与LBP相比，统一模式LBP的模式数量虽然已经减少很多，但是刻画的纹理依然过于精细且模式数量较多。Heikkilä将中心对称思想引入LBP，提出了中心对称局部二值模式。CSLBP重新定义了二进制编码规则，只根据关于邻域中心对称的像素对的差值进行编码。邻域半径为R、点数为P的CSLBP计算方法[9]如式(5)和式(6)所示。

(5)

(6)

其中：Th为预设阈值，用于判别邻域的平坦性。

由式(5)可知，CSLBP的模式最多为2P/2，与LBP和统一模式LBP相比，模式数量大大减小，有利于节约存储空间和降低后续信号分类的复杂度。

3 轴承故障信号分析

3.1 轴承信号描述

笔者采用的滚动球轴承振动加速度信号来自一个单级传动齿轮箱振动试验。试验台架主要由台架基座、电磁调速电机、单级传动齿轮箱、磁粉制动器、联轴器、振动加速度传感器和数据采集设备等组成。测试轴承为SKF6205深沟球轴承，安装在调速电机输出轴上，采用的传感器型号为B&K4508振动加速度传感器，安装在测试轴承座正上方的箱体上。试验通过在轴承的外圈、内圈和滚动体上分别加工直径为0.053 mm的凹槽来模拟轴承的3种常见故障。试验载荷为2.2 kW，采样频率为12 kHz。图3为采集的包括正常状态在内的4种不同状态的轴承振动加速度信号的时域波形。

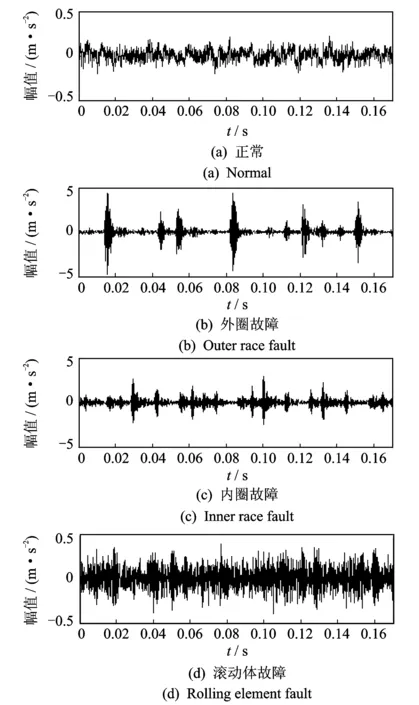
图3 轴承信号时域波形Fig.3 Time-domain waveform of the bearing signal

3.2 轴承信号的广义S变换

对滚动球轴承振动加速度信号进行广义S变换，能否获得分辨性能较好的二维时频图，参数p的取值非常关键。笔者根据式(7)时频聚集性度量准则自适应地选择参数p的取值，具体步骤参见文献[12]。

(7)

其中：GST(t,f)为能量归一化的广义S变换系数，即∑∑GST(t,f)=1；q为大于1的常数，这里设定q=2。

图4 轴承信号的二维时频图Fig.4 Two-dimensional time-frequency images of the bearing signal

图4为4种滚动球轴承振动加速度信号的二维时频图。可以看出，正常信号的能量主要集中在2 kHz及低频部分，内圈和外圈故障信号的能量主要集中在2 kHz～4 kHz之间，并呈现出明显的冲击特征，而滚动体故障信号的能量分布比较分散。不同状态滚动球轴承振动加速度信号的二维时频图表现出明显不同的纹理。由此可知，广义S变换时频图能够很好地描述滚动球轴承振动加速度信号的时频特性，具有一定的可分性。

3.3 基于CSLBP的轴承信号特征提取

二维时频图的维数巨大，例如图4中子图的维数均为1 024×2 048。如果直接将时频图作为滚动球轴承振动加速度信号的的特征参数，则需要巨大的存储空间，并且在轴承信号分类时必然面临严重的“维数灾难”。因此，采用CSLBP对广义S变换时频图进行分析，进一步提取低维的轴承信号特征参数，同时引入LBP和统一模式LBP作为对比。

在参数选择方面，LBP和统一模式LBP涉及2个参数P和R；CSLBP涉及3个参数P，R=1和Th。试验中选取P=8，R=1，Th=0。首先，计算二维时频图的LBP、统一模式LBP和CSLBP；然后，分别统计不同模式值出现的概率，得到对应的纹理谱。由于纹理谱能够有效描述图像的纹理特征，因此笔者以纹理谱作为滚动球轴承振动加速度信号时频特征参数。

图5 轴承信号特征提取结果Fig.5 The feature extraction results of bearing signals

图5为滚动球轴承振动加速度信号时频特征提取结果，每种轴承状态包含5个样本。对比图5(a)和(b)可知，LBP纹理谱的维数为256，重要模式即出现次数较多的模式只有少数，大部分模式出现的概率很小，其在轴承信号特征表达及分类中的贡献很小，属于不重要模式；统一模式LBP纹理谱的维数为59，与LBP纹理谱中重要模式具有较好的对应关系。因此，LBP纹理谱包含大量冗余和无用信息，而统一模式LBP纹理谱利用少量特征参数较好地描述了时频图的重要纹理信息。由图5(c)可以看出，由于编码规则的不同，CSLBP纹理谱的维数仅为16，远小于LBP和统一模式LBP纹理谱的维数，并且具有理想的类内聚合性和较好的类间分散性，呈现出良好的可分性。

因此，与LBP和统一模式LBP纹理谱相比，CSLBP纹理谱无论在特征维数，还是在可分性方面都有明显的优势。

3.4 分类效果

从试验采集的4种状态滚动球轴承振动加速度信号中分别选取40个样本进行分类试验，样本长度均为2 048个点。分类器选用朴素贝叶斯分类器、最近邻分类器和“one-to-one”多分类支持向量机。支持向量机的核函数采用径向基核函数，核参数和惩罚因子通过交叉验证的方法自动选择。为保证结果的有效性，试验重复10次，每次从4类样本中分别随机选取20个样本组成训练样本，其余20个样本组成测试样本。试验结果如图6和表1所示。

图6 轴承信号分类精度Fig.6 The classification accuracy of bearing signals

图6为3种分类器分别采用不同纹理谱对4类滚动球轴承振动加速度信号进行10次分类的平均识别精度。从柱状图可以看出，不管采用什么分类器，LBP、统一模式LBP和CSLBP纹理谱的分类精度都依次提高，且CSLBP纹理谱的分类效果非常理想，分类精度几乎都达到了100%。可见，LBP纹理谱中的大量冗余和无用信息不仅对轴承信号分类没有贡献，反而严重影响了分类精度。统一模式LBP由于仅包含了LBP中的重要模式，冗余和无用信息较少，因而其纹理谱的分类精度大幅度提高。CSLBP因为采用了更为简单有效的二进制编码规则，纹理谱具有更好的类内聚合性和类间分散性，所以获得了比LBP和统一模式LBP纹理谱更高的分类精度。可以看出，CSLBP纹理谱的分类精度受分类器的影响很小，表现出较好的鲁棒性。

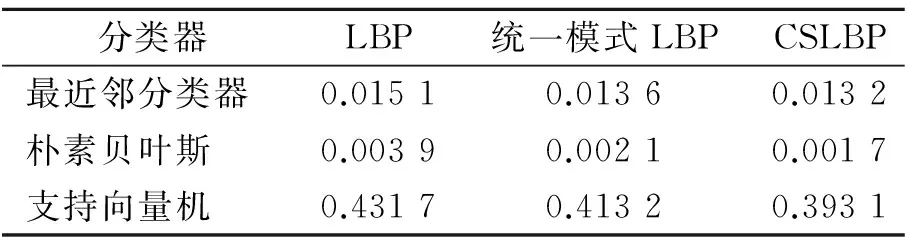
表1为不同分类器分别采用不同纹理谱对4类滚动球轴承振动加速度信号进行10次分类的平均耗时，包括分类器训练时间和测试样本分类时间。从分类器角度而言，朴素贝叶斯分类器速度最快，支持向量机的速度最慢。从特征参数角度而言，由于LBP、统一模式LBP和CSLBP纹理谱的维数依次降低，分别为256,59和16，LBP纹理谱的速度最慢，CSLBP纹理谱的速度最快，统一模式LBP介于二者之间。因此，与LBP和统一模式LBP纹理相比，CSLBP纹理谱的维数更低、分类性能更好，能够有效表达不同状态滚动球轴承振动加速度信号的时频特征。

表1 轴承信号分类时间

Tab.1 The time consumption of bearing signal classification

4 结束语

针对滚动球轴承振动加速度信号时频特征提取问题，引入局部二值模式相关理论，提出了一种基于中心对称局部二值模式的时频特征提取方法。该方法利用广义S变换将一维滚动球轴承振动加速度信号转换为二维时频图，然后基于中心对称局部二值模式，提取时频图的纹理谱作为轴承信号的时频特征参数。将轴承信号广义S变换时频图的中心对称局部二值模式纹理谱与局部二值模式和统一模式局部二值模式纹理谱进行了对比。结果表明，中心对称局部二值模式纹理谱能更好地描述滚动球轴承振动加速度信号的时频特征，并且其分类精度对分类器类型依赖性较小，具有维数低和分类性能好等优点。

[1] 李宏坤, 张志新, 郭正刚, 等. 时频图像Hough变换在滚动轴承故障诊断中的应用[J]. 振动、测试与诊断, 2010, 30(6): 634-637.

Li Hongkun, Zhang Zhixin, Guo Zhenggang, et al. Rolling bearing fault diagnosis using Hough transform of time-frequency image[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6): 634-637.(in Chinese)

[2] 王小玲, 陈进, 从飞云. 基于时频的频带熵方法在滚动轴承故障识别中的应用[J]. 振动与冲击, 2012, 31(18): 29-33.

Wang Xiaoling, Chen Jin, Cong Feiyun. Application of spectral band entropy(SBE) method in rolling bearing fault diagnosis based on time-frequency analysis[J]. Journal of Vibration and Shock, 2012, 31(18): 29-33.(in Chinese)

[3] 赵志宏, 杨绍普. 基于小波包变换与样本熵的滚动轴承故障诊断[J]. 振动、测试与诊断, 2012, 32(4): 640-644.

Zhao Zhihong, Yang Shaopu. Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 640-644.(in Chinese)

[4] 李兵, 米双山, 刘鹏远, 等. 二维非负矩阵分解在齿轮故障诊断中的应用[J]. 振动、测试与诊断, 2012, 32(5): 836-840.

Li Bing, Mi Shuangshan, Liu Pengyuan, et al. Application of two-dimensional non-negative factorization for gear fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 836-840.(in Chinese)

[5] Song Tiecheng, Li Hongliang. Wave LBP based hierarchical features for image classification[J]. Pattern Recognition Letters, 2013, 34: 1323-1328.

[6] Luo Yuan, Wu Caiming, Zhang Yi. Facial expression feature extraction using hybrid PCA and LBP[J]. The Journal of China Universities of Posts and Telecommunications, 2013, 20(2): 120-124.

[7] 杨军, 高志升, 袁红照, 等. 基于LBP特征和贝叶斯模型的单样本人脸识别[J]. 光电子·激光, 2011, 22(5): 763-765.

Yang Jun, Gao Zhisheng, Yuan Hongzhao, et al. Single sample face recognition based on LBP feature and Bayes model[J]. Journal of Optoelectronics·Laser, 2011, 22(5): 763-765.(in Chinese)

[8] Loris N, Alessandra L, Sheryl B. Survey on LBP based texture descriptors for image classification[J]. Expert Systems with Applications, 2012,39: 3634-3641.

[9] Heikkilä M, Pietikäinen M. Description of interest regions with center-symmetric local binary patterns[C]∥Processings of the 5th Conference on Computer Vision, Graphics and Image Processing. Madurai, India:[s.n.], 2006: 58-69.

[10]谭文明, 李斌, 张文聪. 基于中心对称局部二值模式的背景建模方法研究[J]. 中国科学技术大学学报, 2010, 40(11): 1112-1116.

Tan Wenming, Li Bin, Zhang Wencong. Research on background modeling method based on center-symmetric local binary patterns[J]. Journal of University of Science and Technology of China, 2010, 40(11): 1112-1116.(in Chinese)

[11]李欢利, 郭立红, 李小明，等. 基于统计特征中心对称局部二值模式的虹膜识别[J]. 光学精密工程, 2013, 21(8): 2129-2136.

Li Huanli, Guo Lihong, Li Xiaoming, et al. Iris recognition based on SCCS-LBP[J]. Optics and Precision Engineering, 2013, 21(8): 2129-2136.(in Chinese)

[12]Li Bing, Zhang Peilin, Liu Dongsheng, et al. Feature extraction for rolling element bearing fault diagnosis utilizing generalized S transform and two-dimensional non-negative matrix factorization[J]. Journal of Sound and Vibration, 2011, 330: 2388-2399.

[13]Djurovi I, Sejdi E, Jiang J. Frequency-based window width optimization for S-transform[J]. AEU-International Journal of Electronics and Communications, 2008, 62(4): 245-250.

[14]白航, 赵拥军, 胡德秀. 时频图像局部二值模式特征在雷达信号分类识别中的应用[J]. 宇航学报, 2013, 34(1): 139-146.

Bai Hang, Zhao Yongjun, Hu Dexiu. Radar signal recognition based on the local binary pattern feature of time-frequency image [J]. Journal of Astronautics, 2013, 34(1): 139-146.(in Chinese)

[15]Ojala T, Pietikainen M, Maeenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971-987.