综合模态H2范数下致动器/传感器的优化配置*
2016-04-13娄军强魏燕定杨依领谢锋然赵晓伟
娄军强, 魏燕定, 杨依领, 谢锋然, 赵晓伟
(1.宁波大学机械工程与力学学院 宁波, 315211) (2.浙江大学浙江省先进制造技术重点实验室 杭州, 310027)
综合模态H2范数下致动器/传感器的优化配置*
娄军强1, 魏燕定2, 杨依领2, 谢锋然2, 赵晓伟2
(1.宁波大学机械工程与力学学院 宁波, 315211) (2.浙江大学浙江省先进制造技术重点实验室 杭州, 310027)
致动器/传感器的优化配置问题是智能柔性结构振动主动控制中的关键技术问题,基于模态空间H2范数研究了智能柔性梁系统中压电致动器/传感器的优化配置问题。根据Rayleigh-Ritz理论建立了系统的动力学方程并得到其状态空间表达式。提出了一种衡量系统能控/能观性并考虑模态权重的综合模态H2范数准则,采用改进遗传算法研究系统中并置致动器/传感器的优化配置问题,得到了系统多个模态、综合模态H2范数最优的致动器/传感器布局结果。实验结果表明,利用优化结果进行致动器/传感器的布局,系统单个模态和综合模态均具有较好的检测和控制效果,被控模态具有较好的能控/能观性,所提出的优化准则和优化方法是可行的。
智能柔性结构; 综合模态H2范数; 优化配置; 压电致动器/传感器; 改进遗传算法
引 言
为了降低能耗并提高操作效率及精度,机器人和机械操作臂不断朝着低刚度、高精度和柔性化的趋势发展。由于自身低刚度、低阻尼特性,造成柔性机器人及机械臂在执行操作任务过程中很容易激起自身低频、大幅度的弹性振动,因此如何抑制柔性臂的弹性振动是一项具有挑战性的课题[1]。压电材料等智能材料的兴起为振动主动控制技术提供了新的方法和手段。基于压电致动器/传感器的智能柔性结构的振动主动控制技术成为当前的研究热点[2-3]。由于致动器/传感器的分布对系统控制效果具有重要影响,因此研究智能柔性结构中致动器/传感器的优化配置问题具有重要的工程现实意义[4]。致动器/传感器在柔性结构中的优化配置问题引起了国内外学者的广泛关注[5]。Kumar等[6]提出了一个综合考虑输入能量和控制能量的线性二次型调节器(linear quadratic regulator,简称LQR)指标对柔性梁系统中致动器/传感器的位置和控制器参数同时优化。朱灯林等[7]以系统存留能量为目标函数,对悬臂梁结构压电片位置、尺寸和控制进行了融合优化研究。Gueney等[8]在对智能柔性结构的研究中,引入测量误差和外界干扰,对设计的H∞控制器和致动器/传感器布局位置同时优化。研究者尝试从系统结构特性出发,独立于控制器设计得到致动器/传感器的最优布局。Peng等[9]基于最大能控Grammian矩阵准则,研究了柔性板中压电致动器/传感器的配置问题。潘继等[10]使用基于能量的可控Grammian优化准则,研究了柔性悬臂板主动控制中作动器的优化位置问题。Dhuri等[11]以系统固有频率变化率和能控Grammian矩阵奇异值变化率为综合优化指标,基于多目标遗传优化算法研究了柔性结构中致动器/传感器的优化配置问题。钱锋等[12]采用基于主结构模态应变能的优化准则,研究了四边固支复合层压电智能板中的致动器/传感器的位置优化问题。邱志成[13]在挠性悬臂板上致动传感器/致动器的优化配置中提出了基于H2和H∞的复合加权指标。Nestorovic等[14]分别基于系统传递函数的H2范数和H∞范数研究了柔性结构中致动器/传感器的配置问题。对于具有多模态振动的智能柔性结构而言,如何实现系统多个模态以及综合模态的控制/观测效果最佳,仍有许多问题需要深入研究。
笔者针对智能柔性梁系统中压电致动器/传感器的优化配置问题,从表征系统能控/能观性的传递函数H2范数出发,提出了基于整个系统模态空间H2指标并考虑模态权重的致动器/传感器优化配置准则,并搭建实验平台验证相关理论分析和优化结果的有效性。
1 系统建模
以最典型的压电柔性梁为研究对象,粘贴有压电致动器、应变传感器的柔性悬臂梁模型如图1所示。一对压电陶瓷片作为致动器对称地粘贴在距离悬臂梁固定端xp处的上下表面,其致动力矩为M,同时在基体梁的上下表面布局一对应变片传感器用于检测梁的振动情况,其中心到柔性梁固定端的距离为xs。基体梁和压电致动器的几何尺寸长×宽×高分别为Lb×bb×hb和Lp×bp×hp,并假设致动器、传感器与基体梁之间理想粘贴,不存在相对位移。
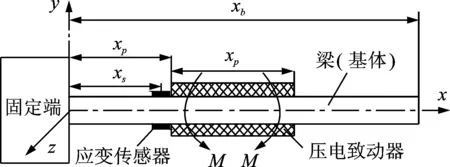
图1 贴有致动器/传感器的悬臂梁模型示意图Fig.1 Model of a cantilever beam with actuators/sensors
由于柔性梁横向振动位移w(x,t)相对于长度尺寸Lb较小,故假设其为Euler-Bernoulli梁模型。根据经典振动理论,压电致动器作用下柔性梁的振动方程为
(1)
其中:Eb为柔性梁的弹性模量;Ib为柔性梁的惯性矩;ρb为柔性梁的密度;Ab为柔性梁的横截面积;xe为压电致动器的终止位置,xe=xp+Lp;δ`(·)为Dirac函数对其变量的导数。
在压电致动器对称布置且理想粘贴的情况下,其致动力矩为
(2)
其中:d31为压电材料的压电应变常数;V为压电致动器的控制电压;c为压电致动器的等效电压系数。
根据Rayleigh-Ritz理论,梁的横向振动位移为
(3)
其中:r为保留的模态阶数;Ф (x)=(φ1,φ2, … ,φr),为模态振型矢量;q(t)=(q1,q2, … ,qr)T,为广义模态坐标矢量。
柔性梁采用一端固定、一端自由的悬臂梁边界条件,得出其第i阶模态振型函数为
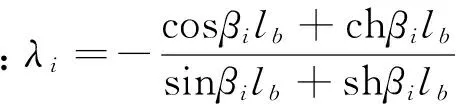
将式(3)和式(2)代入式(1),考虑柔性梁结构阻尼的影响,得到其模态坐标形式的动力学方程为
(5)
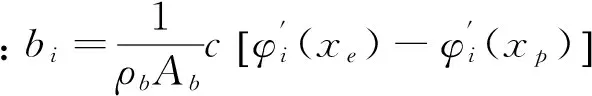
依照图1所示方式粘贴电阻应变片,传感器的输出为柔性梁模态位移的线性组合。采用半桥接法,得到应变片输出电压与柔性臂弹性变形之间的关系为
其中:K为传感器的灵敏度系数;ks为应变传感器的输出电压系数。
引入柔性臂模态位移和模态速度组成的状态变量X,得到系统动力学方程的状态空间表达式为
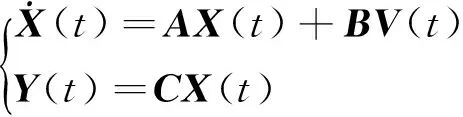
(7)
其中:X(t),Y(t),V(t)分别为状态变量、输出变量和输入变量;A,B,C分别为状态矩阵、输入矩阵和输入矩阵,具体表达式如下

2 模态空间H2范数指标
能控/能观性在系统控制器的设计和应用中占有重要地位。系统的能控/能观性可以通过一些恰当的数值指标体现,如系统能控矩阵/能观矩阵的秩、奇异值、特征值或范数等。对于式(7)所示的智能柔性梁系统,系统输入与输出之间关系的频域表示——传递函数G(iω)为
(8)
系统H2范数的定义[15]为
(9)
其中:G*(ω)为传递函数G(ω)的复共轭。
将式(8)结果代入式(9),化简得到
(10)
其中:Wc为能控Gramian矩阵;Wo为能观Gramian矩阵。
具体表达式如下
(11)
(12)
Wc和Wo的值可通过求解代数Lyapunov线性矩阵方程得到
AWc+WcAT=-BBT
(13)
ATWo+WoA=-CTC
(14)
Gramian矩阵Wc和Wo分别为式(13),(14)的唯一正定Hermitian解。
由于在得到智能柔性梁系统的状态空间方程中采用了模态理论和模态截断技术,在系统结构的模态阻尼比ζi远小于1的情况下,第i阶模态H2范数的表达式[16]为
(15)
其中:Bi为输入矩阵B在第i阶模态坐标上的投影;Ci为输出矩阵C在第i阶模态坐标上的投影。
如果压电致动器和应变传感器采用同位配置的布局方式,仅对单组致动器/传感器在柔性梁上的配置效果进行研究。对于柔性梁的第i阶振动模态,压电致动器输入对应变传感器输出的模态H2范数与式(15)有着相同结果。Bi和Ci的值分别为
(16a)
(16b)
从式(15)可以看出:第i阶模态的H2范数取决于第i阶模态频率ωi,模态阻尼ζi以及输入/输出Lagrange分量Bi和Ci,即某阶模态H2范数越大,代表配置的致动器/传感器分布在该阶模态上的输入/输出分量越大。因此,第i阶模态的H2范数指标反映了在闭环控制下,配置的致动器/传感器将能量引入到系统第i阶振动模态中的能力。
对于具有r阶振动模态的多模态智能柔性梁系统,定义同位布局的致动器/传感器在整个模态空间的H2指标的表达式为
(17)

由于致动器/传感器采用同位配置的方式,因此传感器的粘贴位置为xs=xp+lp/2。建立智能柔性梁系统致动器/传感器优化配置问题的数学模型为
(18)
subjectto:0≤xp≤Lb-Lp
通过在求解空间里寻找如式(18)所示的模态空间H2指标的最大值,即可找到系统能控/能观性最优的致动器/传感器的布局位置,从而实现智能柔性梁系统中致动器/传感器的优化配置。
3 改进遗传算法的优化求解过程
遗传算法(genetic algorithm,简称GA)具有简单易用、适应性强和操作方便的优点,广泛应用于优化问题的求解中[17]。为了提高优化问题的求解精度,加快算法的收敛速度以尽快收敛到最优解,笔者在标准遗传算法的基础上,采用浮点数编码策略和精英保存策略的改进遗传算法完成优化问题的求解,求解过程如下。
1) 确立优化问题模型:建立优化问题的数学模型,并确定可行域,如式(18)所示。
2) 编码并初始化种群:基于浮点数编码策略直接采用待求解变量——致动器配置位置xp组成染色体串进行编码,然后随机产生一定规模数量的初始种群。
3) 个体适应度评估:计算种群个体的目标函数值,并据此评估个体优劣。
4) 选择操作和精英个体保存:根据个体适应度的大小,按照设定概率进行选择操作。为了得到最优解,在选择过程中,根据精英保存策略将适应度最好的个体保存下来。
5) 交叉和变异操作:采用遗传过程中的交叉和变异操作产生新的后代个体。
6) 再次评价个体适应度:重新计算种群个体适应度值,并用保存下来的精英个体替换新种群中的最差个体,提高种群的平均适应度。
7) 终止判断:重复迭代第4步~第6步的操作,直至满足终止条件,得到最优个体。

4 算例分析结果
设定致动器的长度、宽度和厚度都是固定的,仅对其布局位置进行优化。柔性梁、压电致动器的基本参数如表1所示。应变传感器的基本参数如表2所示。

表1 柔性梁和致动器的基本参数表

表2 电阻应变传感器的基本参数
由于高阶模态在柔性梁振动模态中所占比重较少,重点关注柔性臂前两阶模态的能控/能观性。根据表1参数,采用悬臂梁边界条件计算得到柔性梁的前两阶固有频率为3.89Hz和24.4Hz,并设定相应的模态阻尼比分别为0.02和0.01。
在具体的优化求解过程中,遗传算法的基本参数设置:种群大小为50,最大进化代数为50,交叉概率为0.6,变异概率为0.01并通过多次优化以求得最优解。图2为以柔性梁一阶模态的H2范数为优化目标的遗传进化过程。可以看出,大约经过25代进化过程收敛到最优解。表3为以柔性梁的一阶模态、二阶模态以及综合模态H2范数为优化目标得到的最终优化结果。可以看出:当压电致动器/应变传感器布局在柔性梁的根部位置距固定端0.403 mm时,系统一阶模态H2范数最大为2.74×10-5;当致动器/传感器配置在柔性梁的中部位置距固定端276.136mm时,系统二阶模态H2范数取得最大值1.90×10-5;当致动器/传感器布局在柔性梁的根部位置距固定端1.332 mm时,综合模态H2范数取得最大值3.86×10-5(注:模态H2范数与适应度互为倒数)。

图2 平均及最佳适应度的遗传进化过程Fig.2 Evolution process of the mean and best fitness
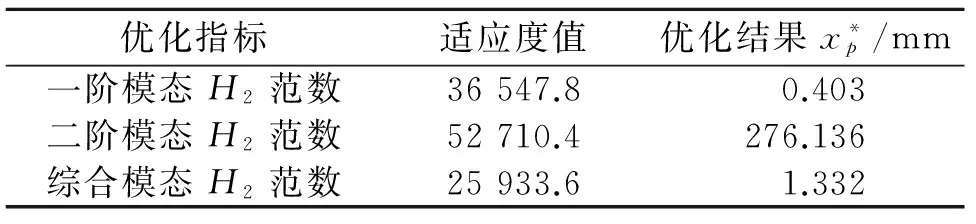
优化指标适应度值优化结果x*p/mm一阶模态H2范数36547.8 0.403二阶模态H2范数52710.4276.136综合模态H2范数25933.61.332
5 实验研究
搭建智能柔性梁测控系统如图3(a)所示。根据优化结果及实际布线考虑,为了获得柔性梁最大的振动信息,将一组电阻应变片对称地粘贴在梁的根部位置,在靠近应变片的位置距离根部24.7mm处,对称地粘贴第1组压电陶瓷片作为致动器。为了比对不同位置的致动器/传感器的致动/检测效果,在柔性梁的中部位置,也就是距离柔性梁根部260.2mm和280.3mm的地方分别布局第2组应变传感器和压电致动器,实物图如图3(b)所示。整个测控系统以工控PC机为控制中心,传感器的检测信号经滤波后通过多路应变放大器放大为-10~+10V的电压信号,工控机发出的控制电压信号(±10V)经多路功率放大器放大为-150~+150V施加在压电致动器上,并利用多通道的数据采集卡实现数据D/A, A/D转换,实现传感信号输入和控制信号输出功能。
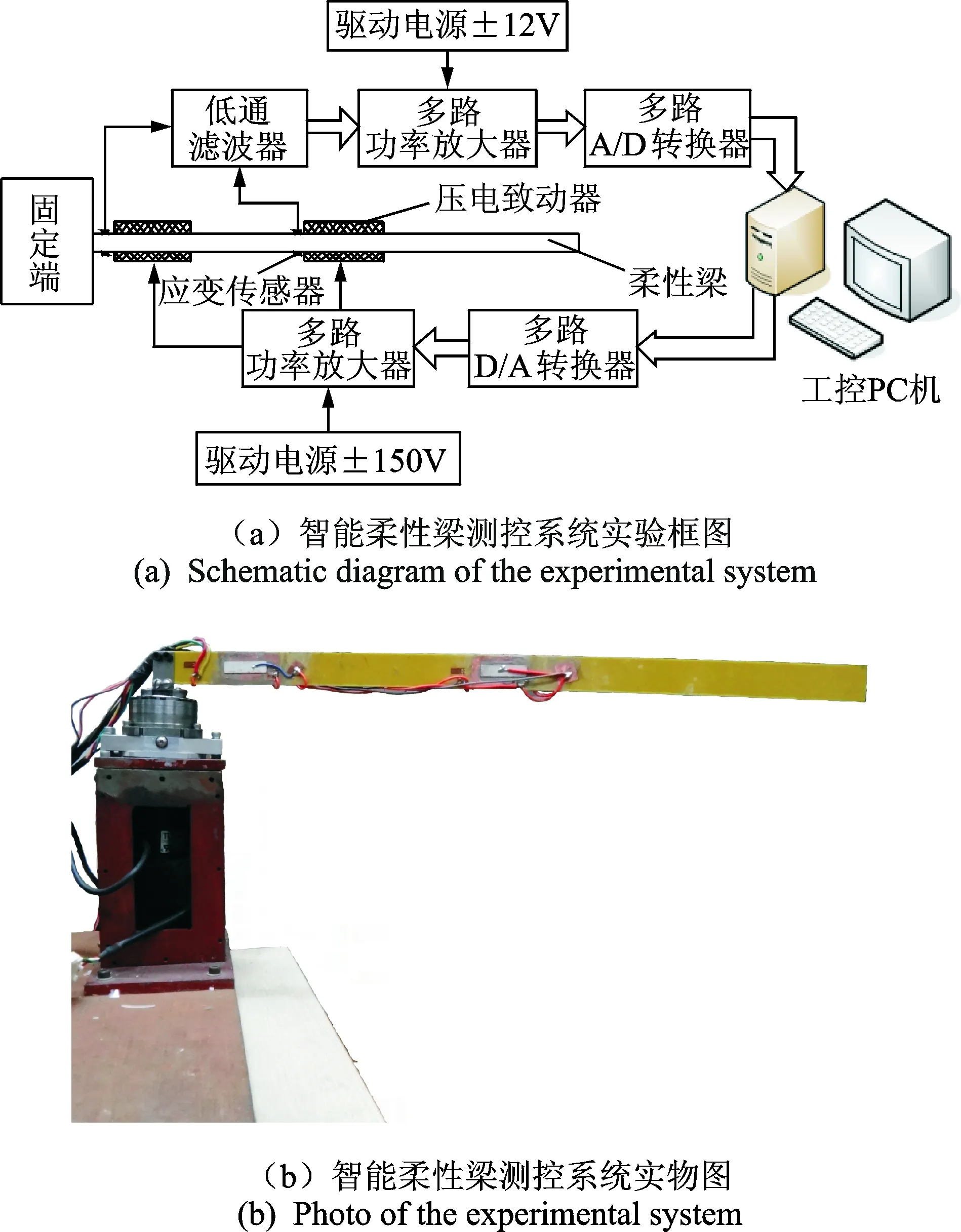
图3 智能柔性梁测控系统实验框图及实物图Fig.3 Schematic diagram and photo of the experimental system
为了掌握系统的动态特性,进行智能柔性梁系统的模态特性实验。通过冲击锤敲击激起柔性梁的振动,并用截止频率为35.0Hz的低通巴特沃斯滤波器滤波,经计算得到柔性梁的前两阶固有频率和模态阻尼比分别为f1=2.8Hz,ζ1=0.022,f2=17.8Hz,ζ2=0.009。显然,压电致动器和应变传感器的加入以及材料实际特性与标称值的差异造成了实验结果与理论分析之间的差异。因此,从实验角度实际检验致动器/传感器的配置效果很有必要。
由于系统一阶模态固有频率较低,故外界干扰易激起其弹性振动。在柔性梁根部的压电致动器施加一个与系统一阶固有频率同频、持续时间为14s的正弦信号
fd(t)=140.0sin(2π2.81t)
(19)

图4 根部致动器激励下传感器的输出信号Fig.4 Output signals of sensors actuated by root PZT actuators
的激励下,粘贴在柔性梁根部的应变传感器的输出信号如图4所示。图5为将同样的激励信号施加到粘贴在柔性梁中部的压电致动器时,粘贴在柔性梁根部应变传感器的输出信号。图6为两种情况下频域信号的对比情况。从图4和图5的实验结果可以看出,同样在与系统一阶固有频率同频的驱动信号激励下,布局在根部的压电致动器激起了系统更大的一阶模态振动(见图6)。与配置在柔性梁中部的致动器相比,布局在根部的致动器对柔性梁的一阶模态振动具有更强的致动能力,对系统一阶模态的控制能力更强,此时系统一阶模态的能控性更好。
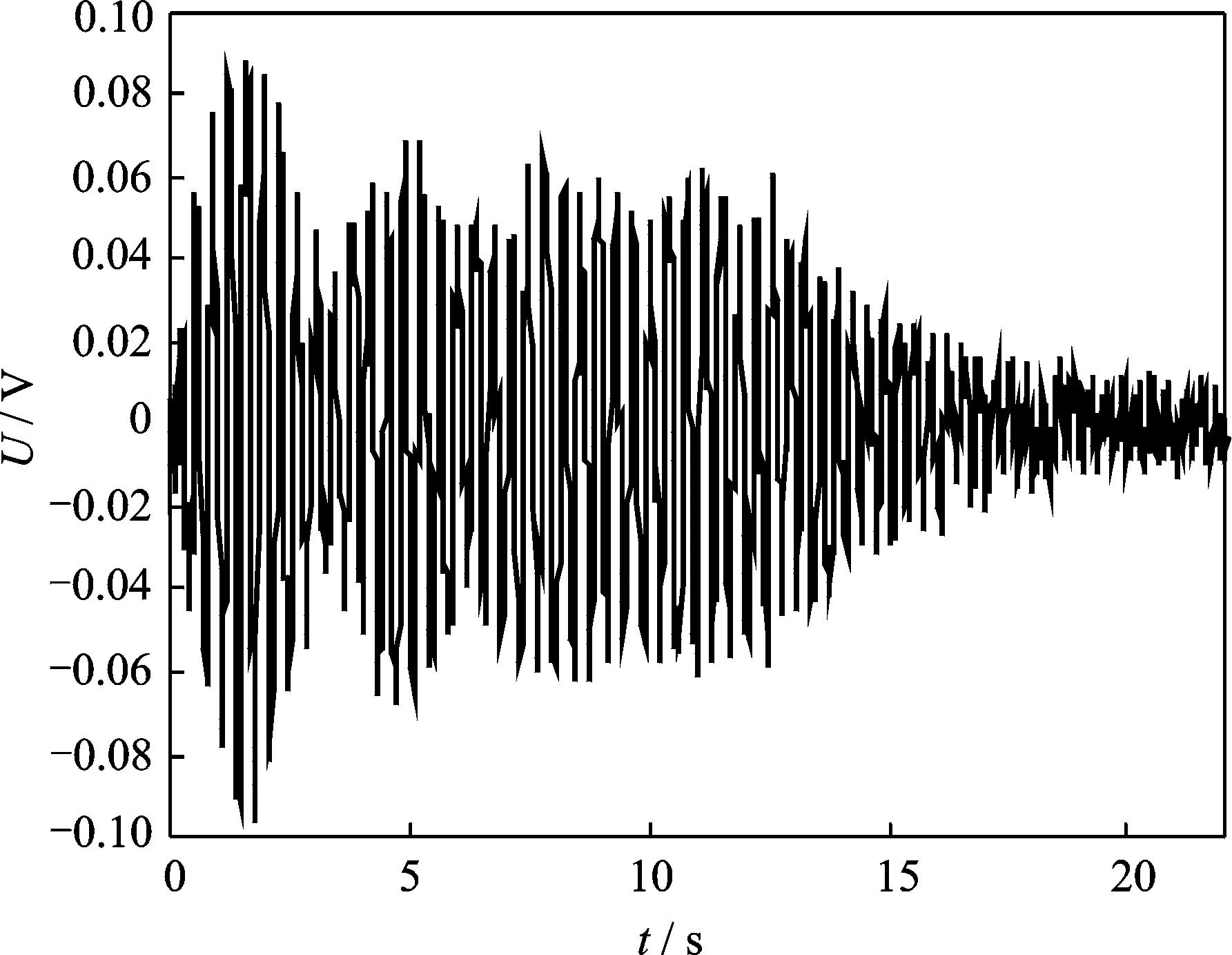
图5 中部致动器激励下传感器的输出信号Fig.5 Output signals of sensors Actuated by middle PZT actuators

图6 不同位置致动器激励下传感器的频域信号Fig.6 Compared frequency response actuated by PZT actuators in different position
图7和图8为在一次冲击信号激励下粘贴在柔性梁根部和中部的应变片传感器的输出信号。二者频域信号的对比情况如图9所示,显然布局在柔性梁根部的传感器对系统一阶模态的传感检测能力较强,能观性更好。从图6和图9的实验结果可以得出,当致动器/传感器布局在柔性梁根部时,系统一阶模态的能控/能观性最好,理论优化配置结果的有

图7 同一激励信号下根部传感器的输出信号Fig.7 Output signals of root sensors stimulated by a signal

图8 同一激励信号下中部传感器的输出信号Fig.8 Output signals of middle sensors stimulated by a signal

图9 同一信号激励下不同位置传感器的频域信号Fig.9 Compared frequency response of sensors in different position stimulated by a signal
效性得到了验证。
对系统二阶模态的检测情况而言,当传感器布局在柔性梁中部位置时,传感器此时具有更好的检测输出能力,如图9中二阶频率波峰所示,其检测输出的系统二阶模态振动幅值大于根部传感器的输出,二阶模态的能观性更好。根据并置致动器/传感器的能控/能观性的一致性,显然系统二阶模态H2范数在柔性梁中部取得最大值,此时系统二阶模态的能控/能观性最好。如图4~9的实验结果所示,由于一阶模态占据主导地位,故系统的综合模态H2范数仍是致动器/传感器配置在柔性梁根部时取得最大值,此时系统综合模态的能控/能观性最好。
从实验结果可以看出:虽然压电致动器的引入对柔性臂系统的模态特性产生了一定影响,但是布局在根部的传感器对系统一阶模态具有更好的检测传感效果,而布局在中部的传感器对系统二阶的检测传感效果更好,且由于一阶模态占主导地位,根部传感器的输出明显高于中部,综合模态的能控性更好。对于压电致动器的布局,虽然实际布线需要第1组压电致动器布局在靠近柔性梁根部的位置,而非优化得到的最大综合模态指标处—柔性梁的根部,但与第2组压电致动器的实际控制效果相比,其对系统一阶模态仍具有更强的驱动和控制效果,也可以为理论分析结果提供一定的依据。
6 结 论
1) 研究了智能柔性结构中压电致动器/应变传感器的优化配置问题。提出了一种衡量系统能控/能观性并考虑模态权重的模态空间H2范数准则,采用改进遗传算法研究了智能柔性梁系统中并置致动器/传感器的优化配置问题,并搭建实验平台验证了理论分析和优化结果的有效性。
2) 结果表明:所提出的优化准则和优化方法是切实可行的。该方法可以应用到其他复杂的柔性结构,为智能柔性结构中致动器/传感器的优化配置提供借鉴和尝试。
[1] 褚明, 贾庆轩, 叶平, 等. 关节驱动柔性臂非最小相位系统的全局终端滑模控制[J]. 机械工程学报,2012(3): 41-49.
Chu Ming, Jia Qingxuan, Ye Ping, et al. Global terminal sliding mode control for joint-drive flexible arm non minimum phase system[J]. Chinese Journal of Mechanical Engineering, 2012, 48(3): 41-49. (in Chinese)
[2] Dutta R, Ganguli R, Mani V. Swarm intelligence algorithms for integrated optimization of piezoelectric actuator and sensor placement and feedback gains[J]. Smart Materials & Structures, 2011, 20: 1-14.
[3] 李雨时, 周军, 钟鸣, 等. 基于压电堆与橡胶的主被动一体化隔振器研究[J]. 振动、测试与诊断,2013, 33(4): 571-577.
Li Yushi, Zhou Jun, Zhong Ming, et al. Active and passive integration of vibration isolator based on piezoelectric-rubber[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(4): 571-577. (in Chinese)
[4] Gupta V, Sharma M, Thakur N. Optimization criteria for optimal placement of piezoelectric sensors and actuators on a smart structure: a technical review[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(12): 1227-1243.
[5] 吕永桂, 陈凯, 魏燕定. 智能杆致动器优化配置及扭振主动控制试验[J]. 振动、测试与诊断,2010, 30(4): 400-404.
Lü Yonggui, Chen Kai, Wei Yanding. Intelligent actuator placement and active torsional vibration control experiment on a circular tube[J]. Journal of Vibration, Measurement and Diagnosis, 2010, 30(4): 400-404. (in Chinese)
[6] Kumar K R, Narayanan S. Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs[J]. Smart Materials & Structures, 2008, 17: 1-15.
[7] 朱灯林, 吕蕊, 俞洁. 压电智能悬臂梁的压电片位置、尺寸及控制融合优化设计[J]. 机械工程学报, 2009, 45(2): 262-267.
Zhu Denglin, Lü Rui, Yu Jie. Integrated optimal design of the PZT position, size and control of smart cantilever beam[J]. Chinese Journal of Mechanical Engineering, 2009, 45(2): 262-267. (in Chinese)
[8] Gueney M, Eskinat E. Optimal actuator and sensor placement in flexible structures using closed-loop criteria[J]. Journal of Sound and Vibration, 2008, 312(1-2): 210-233.
[9] Peng Fujun, Ng A, Hu Yanru. Actuator placement optimization and adaptive vibration control of plate smart structures [J]. Journal of Intelligent Material Systems and Structures, 2005, 16(3): 263-271.
[10]潘继, 陈龙祥, 蔡国平. 柔性板压电作动器的优化位置与主动控制实验研究[J]. 振动与冲击, 2010, 29(2): 117-120.
Pan Ji, Chen Longxiang, Cai Guoping. Optimal positioning of PZT actuators and active control testing for a flexible plate[J]. Journal of Vibration and Shock, 2010, 29(2): 117-120. (in Chinese)
[11]Dhuri K D, Seshu P. Multi-objective optimization of piezo actuator placement and sizing using genetic algorithm[J]. Journal of Sound and Vibration, 2009, 323(3-5): 495-514.
[12]钱锋, 王建国, 汪权, 等. 基于模态应变能分布的压电致动器/传感器位置优化遗传算法[J]. 振动与冲击, 2013, 32(11): 161-166.
Qian Feng, Wang Jianguo, Wang Quan, et al. Optimal placement of piezoelectric actuator/sensor using genetic algorithm based on modal strain energy distribution[J]. Journal of Vibration and Shock, 2013, 32(11): 161-166. (in Chinese)
[13]邱志成. 挠性板振动抑制的敏感器与驱动器优化配置[J]. 宇航学报, 2002, 23(4): 30-36.
Qiu Zhicheng. Optimal placement of sensors and actuators for flexible plate of vibration suppression[J]. Journal of Chinese Society of Astronautics, 2002, 23(4): 30-36. (in Chinese)
[14]Nestorovic T, Trajkov M. Optimal actuator and sensor placement based on balanced reduced models[J]. Mechanical Systems and Signal Processing, 2013, 36(2): 271-289.
[15]Armaou A, Demetriou M A. Optimal actuator/sensor placement for linear parabolic PDEs using spatial H-2 norm[J]. Chemical Engineering Science,2006, 61(22): 7351-7367.
[16]Qiu Zhicheng, Zhang Xianming, Wu Honghua, et al. Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate[J]. Journal of Sound and Vibration, 2007, 301(3-5): 521-543.
[17]Bruant I, Gallimard L, Nikoukar S. Optimal piezoelectric actuator and sensor location for active vibration control, using genetic algorithm[J]. Journal of Sound and Vibration, 2010, 329(10): 1615-1635.

10.16450/j.cnki.issn.1004-6801.2016.01.008
*国家自然科学基金资助项目(51505238,51375433);浙江省自然科学基金资助项目(LQ15E050002);宁波市自然科学基金资助项目(2015A610145);宁波大学学科项目(xkl141034)
2014-01-06;修回日期:2014-03-10
TP24; TH113
娄军强,男,1986年7月生,讲师。主要研究方向为振动主动控制、智能材料应用等。 E-mail: loujunqiang@nbu.edu.cn 通信作者简介:魏燕定,男,1970年7月生,教授、博士生导师。主要研究方向为机械制造及自动化。 E-mail: weiyd@zju.edu.cn
