基于次级通道在线辨识新算法的振动主动控制*

2016-04-13浦玉学姜金辉

振动、测试与诊断 2016年1期

关键词：作动器控制点滤波器

浦玉学, 张方，姜金辉，徐菁，蒋祺

(南京航空航天大学机械结构力学与控制国家重点实验室南京，210016)

基于次级通道在线辨识新算法的振动主动控制*

浦玉学, 张方，姜金辉，徐菁，蒋祺

(南京航空航天大学机械结构力学与控制国家重点实验室南京，210016)

提出一种基于改进滤波型最小均方(filtered-X least mean square, 简称FXLMS)算法次级通道在线辨识方法，将其应用到结构自适应振动主动控制中。该算法可以消除主动控制环节和次级通道辨识环节相互影响，加快系统的收敛速度，并有效消除附加随机信号对待控制区域残余振动的影响，简化了系统算法的复杂度。将该方法基于LABVIEW进行振动控制仿真，从收敛性能和振动控制效果两方面进行比较，得出其改进优势。以简支梁为控制对象,用本研究方法进行结构振动主动控制的试验研究。结果表明，该控制系统对简支梁的振动响应有很好的抑制作用,说明该基于次级通道在线辨识的主动控制方法的有效性。

振动主动控制；次级通道在线辨识；自适应滤波；滤波型最小均方算法

引言

在实际工程应用中，结构的扰动或不必要的大幅振动会破坏结构性能，导致不稳定甚至引发灾难性后果。振动主动控制能有效抑制扰动，弥补被动控制的缺点，具有减振效果好、功耗低和自适应性强的特点，成为近年来振动控制领域的研究热点[1]。

文献[2-3]就主动控制算法应用到振动控制领域做了综合型概述。自适应振动主动控制方法基本原理采用在结构上直接附加力源 (或称次级振源)，通过自适应控制律调节输出控制信号，驱动作动器激发结构次级振动，与初级振动相抵消，达到振动控制的目的。自适应主动控制系统区别于自适应信号处理系统在于前者存在次级通道(次级振源到误差传感器之间的通道)。次级通道特性对振动主动控制算法实现、系统的收敛性以及控制效果有着重要影响。最常用的自适应主动控制算法是将次级通道考虑在内的滤波型最小均方算法[4-5]。次级通道的辨识误差对主动控制系统的影响在文献[6-7]中做了讨论。次级通路特性对有源控制系统的影响表现在两个方面：a.次级通路辨识误差影响系统稳定性和降噪效果；b.次级通路辨识参数影响自适应算法运算量，当滤波器长度增加到一个值时，引起的运算量的增大可能会超出控制器所能承受的范围。如何对次级通道进行快速、精确的辨识，是振动主动控制系统设计必须考虑的关键问题之一。对次级通道辨识有离线辨识和在线辨识两种，如果在主动控制期间，次级通路的系统特性基本保持不变或变化缓慢，采用离线辨识方式能简化控制算法。当系统特性改变比较明显时，应该采用在线辨识以确保满足控制系统的稳定性和控制精度的要求。

笔者基于最简单的前馈式FXLMS控制模型，对次级通路在线辨识算法进行改进。在尽量减少自适应滤波器数目、降低算法复杂度的原则下，消除主动控制环节和次级通道辨识环节相互影响，加快系统的收敛速度，并有效消除附加随机信号对待控制区域残余振动的影响。从收敛性能和算法计算量两方面跟传统算法进行比较，得出其改进优势。

1 常规的在线辨识算法

基本的次级通道在线辨识方法是由Eriksson等[8]提出的附加随机噪声方法，如图1所示。图中：P(n)为初级振源(激振器)到待控制点的传递函数；S(n)为由作动器到待控制点的次级通路的传递函数,是一个非常复杂电声耦合系统,其主要由D/A转换、扬声器、次级声通道和A/D转换等部分组成；x(n)为参考信号；e(n)为指待控制点处误差传感器检测到的残余振动响应信号。

随机噪声v(n)作为次级通道自适应在线辨识滤波器S′(n)的输入。当辨识滤波器收敛后，S′(n)可惟一收敛到S(n)，在自适应控制过程中S′(n)可作为次级通道S(n)的估计传递函数;但是这种方法会在作动器的输入端y(n)加入随机噪声并通过次级通道引起待控制点额外振动，且该振动在整个次级通道的辨识过程中都无法剔除。

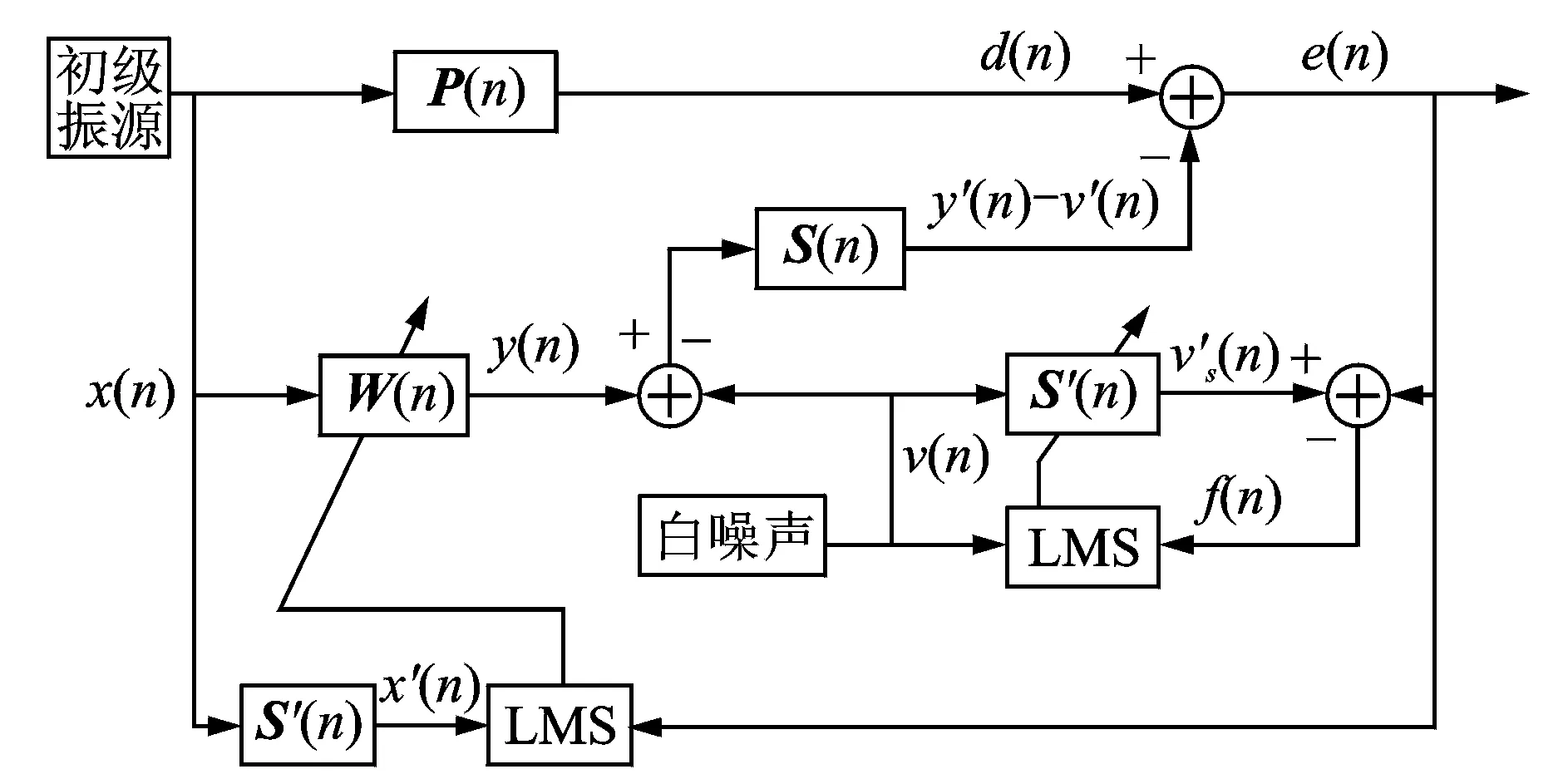
图1 Eriksson次级通道在线辨识算法框图Fig.1 Eriksson′s algorithm for online secondary path modeling

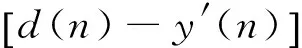
图2 杨铁军次级通道在线辨识算法框图Fig.2 Yang′s algorithm for online secondary path modeling

2 改进的在线辨识算法

文献[11]的算法虽然试图消除次级通道辨识环节和主动控制环节的相互影响，但由于算法中涉及到的自适应滤波器太多，增加了算法的计算量，而且控制前需要预设3个收敛因子，收敛因子的大小又对控制系统的性能产生很大影响，这大大局限了该算法的实用性。在保证消除主动控制环节与次级通道辨识环节相互影响的前提下，避免使用第3个自适应滤波器H(n)是笔者工作的重点。为此，构造了如图3所示的基于次级通道在线辨识的自适应控制系统。该算法将文献[11]算法中第3个滤波器与主动控制滤波器相结合，构造了新型的自适应滤波器。与文献[11]算法相比，减少了一个自适应滤波器，简化了算法，降低了算法的计算量，提高了主动控制系统的收敛速度。

图3 本研究改进次级通道在线辨识算法框图Fig.3 Proposed algorithm for online secondary path modeling

主动控制器权系数通过FXLMS算法迭代更新

(1)

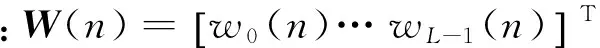
(2)

其中：S(n)为次级通道脉冲响应函数；XM(n-1)=[x(n)…x(n-M+1)]T。

(3)

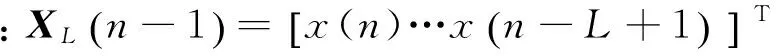
由于在主动控制器输出端附加与参考信号x(n)不相关的随机高斯白噪声，该随机噪声会在待控制点的残余振动量e(n)中体现出来

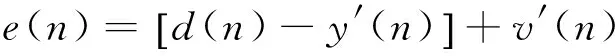
(4)

进一步推导有

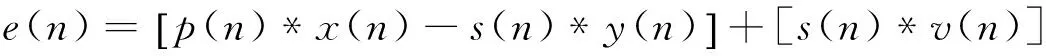
[s(n)*v(n)]作为次级通道在线辨识环节引入附加随机噪声对主动控制环节的收敛性能的影响，尤其当W逼近Wopt时，这种影响更为明显。

定义次级通道在线辨识滤波器S′(n)为长度为M的FIR型滤波器。附加随机噪声v(n)经过S′(n)的输出为

(5)

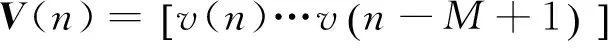
2.1 主动控制滤波环节

由于存在次级通道，这里讨论的方法的主动控制环节均为基于FXLMS算法。FXLMS算法与LMS算法的稳态和瞬态特性总体趋势都是相同的，但由于次级通道的引入，对算法性能影响很大。研究表明，次级通道中各环节引入的信号幅度变化，而时延对算法的收敛性影响是主要的。

在图4所示的FXLMS算法中，在离散时域内对FXLMS算法进行分析，主动控制滤波器的误差信号为

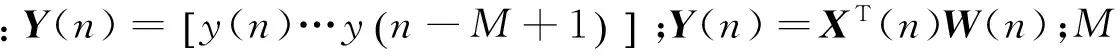
如果将x(n)经过S′(n)滤波的信号作为参考输入，笔者构造算法的主动控制环节可看作参考信号为x′(n)，期望信号为d(n)的LMS算法。图5为改进的FXLMS算法。对于主动控制环节

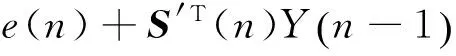
这样基于FXLMS算法的主动控制滤波环节便转换为基于LMS的迭代算法，这大大改善了振动主动控制系统的收敛性能。

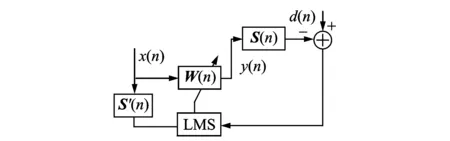
图4 FXLMS算法框图Fig.4 FXLMS algorithm

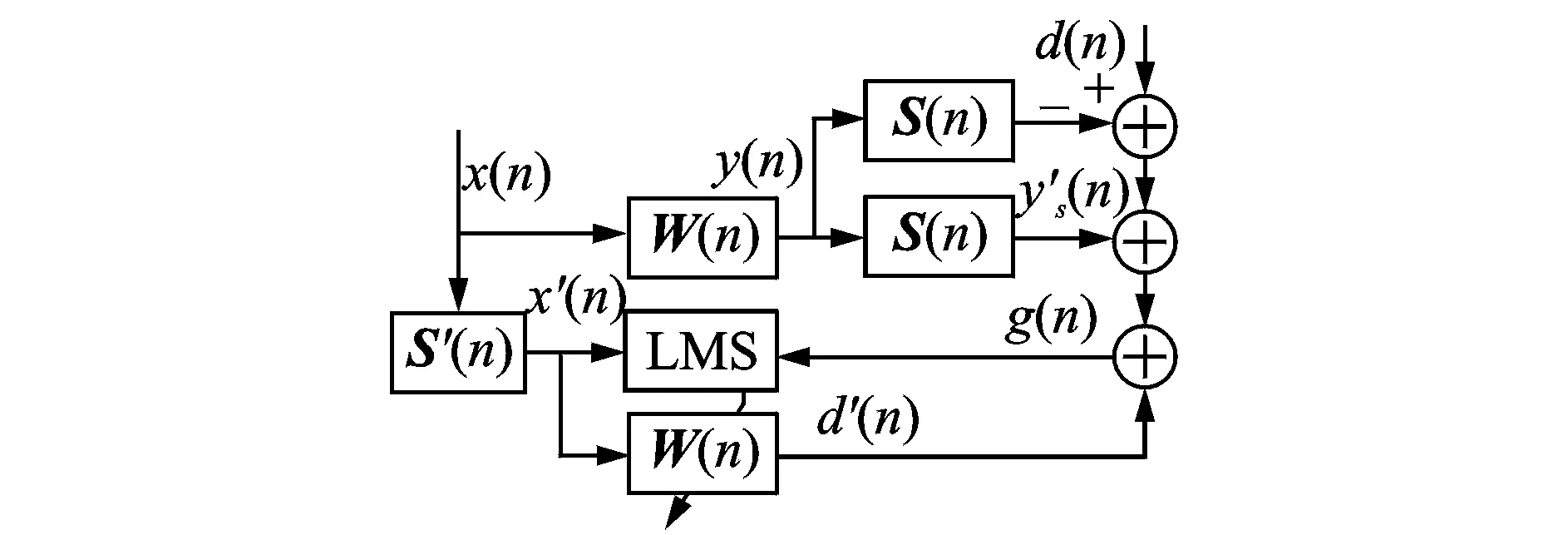
图5 改进FXLMS算法框图Fig.5 Modified FXLMS algorithm

不失一般性，这里假设次级通道仅包含幅度变化和时延。在z变换域下，次级通道可表示为

(6)

其中：ks为次级通道的无量纲时延，它表示离散时域内以采样点为单位的时延个数。

其中：ts为振动由作动器作用点传到待控制点需要的时间；fs为采样率；Fix(x)为取整函数。

通过对FXLMS算法收敛性分析可知，要保证算法收敛并保持稳定，收敛因子需满足

(7)

其中：λmax为滤波参考信号x′(n)自相关矩阵的最大特征值。

笔者将FXLMS算法变化为以x′(n)为参考输入的LMS自适应算法，该算法收敛并保持稳定的条件，收敛因子满足

(8)

其中：λmax为参考信号x′(n)自相关矩阵的最大特征值。

比较式(7)和式(8)可以看出，由于次级通道的存在，FXLMS算法的收敛系数取值范围比LMS算法要小ks倍。这说明为了保持系统稳定，FXLMS算法权系数自适应调整的步距比LMS算法小ks倍，收敛时间也慢了ks倍。通过将FXLMS算法转化为LMS算法，将主动控制滤波环节的收敛速度提高。可见，采用笔者构造的算法不仅避免文献[11]算法中第3个滤波器的出现，降低算法的复杂度，而且用LMS算法取代FXLMS算法提高了算法的快速收敛性。

权系数更新过程为

(9)

(10)

理想情况下,S′(n)=S(n),g(n)=d(n)-X′T(n)W(n)。g(n) 与x(n)完全相关,因此附加随机噪声v(n) 对主动控制器权向量收敛过程的影响就被完全消除了。

2.2 次级通道在线辨识环节

根据文献[11]的算法，当次级通道在线辨识滤波器完成收敛后，实现了消除附加随机噪声对主动控制滤波环节收敛性能的影响，但是用误差信号g(n)作为次级通道在线辨识滤波器权系数更新的误差信号，无法实现主动控制环节对次级通道辨识环节影响的完全消除。

在文献[11]算法中，次级通道在线辨识滤波器权系数通过LMS算法迭代更新为

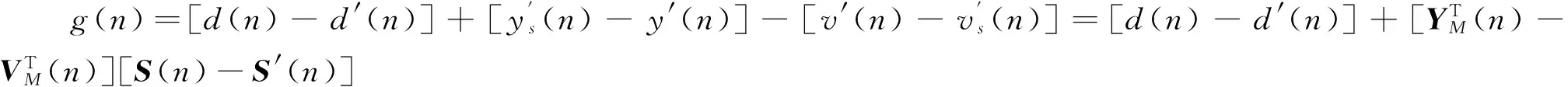
当W(n)收敛到Wopt时，d(n)-d′(n)=0,d(n)=y′(n),g(n)不能做到与附加随机信号v(n)完全相关，它还与控制信号y(n)存在相关性，这说明主动控制环节对在线辨识环节的影响未完全消除。

为了弥补这个缺憾，笔者采用信号f(n)作为次级通道在线辨识滤波器权系数更新的误差信号。

(11)

对f(n)进一步分析

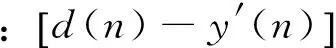
当W(n)收敛时，d(n)-y′(n)=0,g(n)与v(n)完全相关分量，主动控制环节对在线辨识环节的影响至此完全消除。

2.3 附加随机噪声调整策略

通过在控制信号中附加随机噪声实现次级通道的在线辨识存在一个难以忽视的问题，附加的随机白噪声会在待控制的残余振动量中体现出来。采用大功率的白噪声有利于次级通道的辨识，降低了主动振动控制的减振效果。为了协调这一矛盾点，笔者提出一种附加随机噪声的调整策略。

其中：vm(n)为幅值为1的单位高斯白噪声信号。

其中：Pf(n)，Pe(n)为误差信号f(n)和e(n)的功率，采用指数平滑预测方法计算

由于v′(n) 与d(n)和y′(n)不相关，对G(n)进一步推导可得

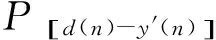
考虑到当初级振动量功率较大时，需要较大的随机噪声用于次级通道的在线辨识，否则小功率的附加白噪声会被强干扰信号淹没，这里将参考信号的功率考虑到附加随机噪声的调整策略中，最终附加随机噪声的调整策略为

(12)

(13)

2.4 算法与计算量分析

表1为笔者提出的算法与计算量分析。其中：M和N分别为FIR型主动控制滤波器和次级通道辨识滤波器的长度。

表2为单次迭代计算量比较。其中：M，N为初级通道、次级通路等效为FIR滤波器权系数阶数；H为文献[10-11]方法中第3个滤波器权系数阶数。

表1 本研究算法与计算量统计

表2 单次迭代计算量比较

算例中M=32,N=32,H=64

从表2可知：笔者改进算法的计算量远少于文献[10-11]算法的计算量，这是因为笔者提出的次级通道在线辨识方法比文献[10-11]的算法少了一个自适应滤波器，算法上有很大的简化。计算略多于Eriksson算法，是因为改进FXLMS的引入，而这是为了更好地消除主动控制环节和次级通道辨识环节相互影响。

3 仿真算例

为了评价笔者提出的次级通道在线辨识算法的性能,基于LABVIEW语言将Eriksson算法、文献[11]和笔者改进算法进行主动控制的仿真。

为了准确衡量在线辨识的收敛性能辨识的精确性，定义次级通路辨识误差为

(14)

为了直观地衡量系统的减振性能，定义衡量标准为

(15)

R(n)值越大，则系统降噪量越大，反之亦然。

仿真之前需要设置初级通路和次级通路的传递函数初级通路的传递函数分别设为10阶和16阶FIR型滤波器，控制滤波器权系数W(n)和S′(n)长度分别为32和32。文献[11]算法中第3个滤波器长度为64。初级通路的传递函数可以设为

H(z)=0.05-0.001z-1+0.001z-2+0.8z-3+

次级通路的传递函数设为

S(z)=0.03-0.04z-1+0.8z-2+0.1z-3-

0.3z-4+0.2z-12+0.04z-13-0.01z-14+0.6z-15

3.1 定频振动信号控制算例仿真

设初级振动信号为一正弦信号与高斯白噪声合成信号，信噪比为30dB。正弦信号频率为50Hz，幅值为2。附加随机噪声为零均值高斯白噪声信号，标准差为0.1。仿真结果如图6所示。

Eriksson算法参数设置为μw=5×10-3，μs=2×10-2。文献[11]算法参数设置为μw=5×10-3，μs=1×10-2，μh=1×10-2。笔者改进算法参数设置为μw=5×10-3，μs=2×10-2。

如图6(a)所示，笔者改进算法相对于Eriksson和文献[11]算法，次级通道辨识误差ΔS(n)很快稳定下降到-42dB，这说明次级通道估计值能快速收敛于次级通道的真实值。图6(b)为笔者改进算法与上述两种算法在降噪性能R(n)的比较。可见，通过自适应调节主动控制环节收敛步长的大小，笔者改进算法表现出了更好的减振性能。附加随机噪声控制系数G(n)随迭代次数的变化曲线如图6(c)所示。当控制系统开始工作初期，为了使次级通道辨识滤波器快速收敛，需要较大的附加随机噪声，G(n)维持较大值。随着次级通道估计值逐渐收敛到真实值时，G(n)的值相应的降低到零，这样附加随机噪声对待控制点残余振动量的叠加就被消除了。

3.2 次级声道突变控制算例

现考虑一种特殊情况：次级声道在控制过程中突然发生变化。仿真控制系统的参考信号、附加随机噪声信号以及突变前的次级通道均按照以上情况设置，在系统迭代到40 000次时，次级通道产生突然变化。

0.04z-13+0.6z-15

次级通道辨识误差ΔS(n) 变化曲线如图7(a)所示。可以看出，笔者提出算法可以将次级通道辨识误差降低，而且在次级通道突然变化后依然表现出了快速收敛性。尤其是附加随机噪声控制系数G(n)在次级通道突变后迅速增大(见图7(c))，以提供较大的附加随机噪声用来次级通道的在线辨识。从图7(b)可以看出，在次级通道变化前后，采用笔者提出的次级通道在线辨识方法的主动控制系统取得了最好的减振效果。

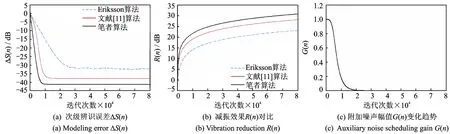
图6 简谐振动主动控制仿真结果Fig.6 Performance Comparison on fixed-frequency active control simulation

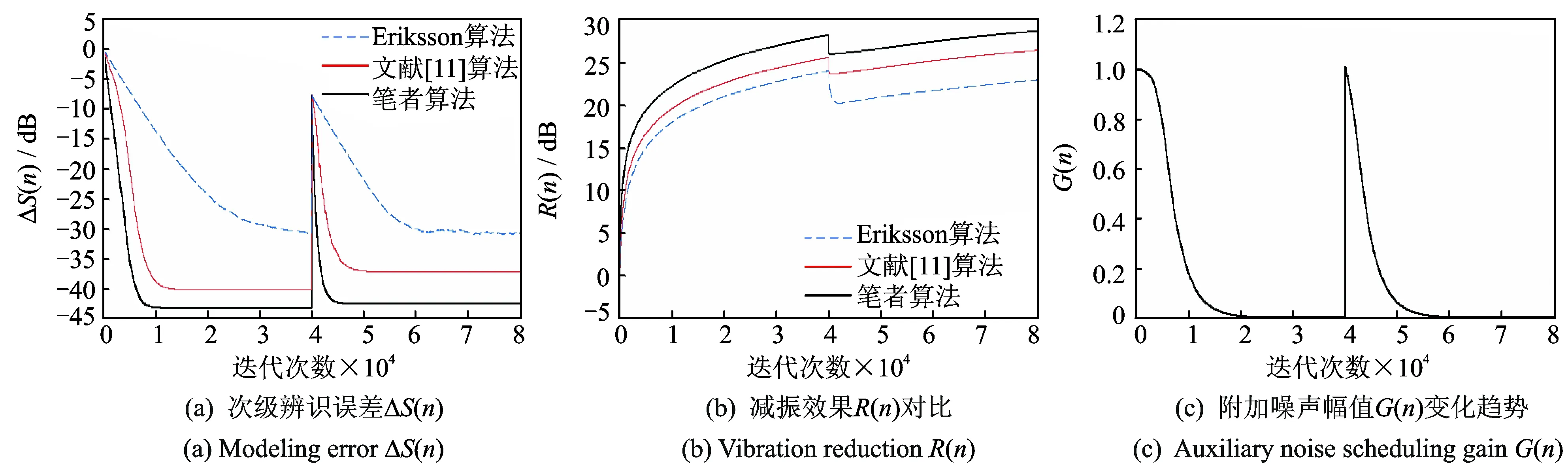
图7 次级通道突变控制仿真结果Fig.7 Performance Comparison on secondary path change simulation

4 试验研究

为了对笔者提出的次级通道在线辨识技术的效果进行验证，基于美国国家仪器公司的可重新配置嵌入式控制盒采集系统(NICRIO) 进行了简支梁振动主动控制试验。简支梁长为1 600mm,宽为50mm,厚为10mm。试验基本原理如图8所示。信号发生模块生成参考信号，经功率放大器传给激振器，激发简支梁的初级振动。加速度传感器接收到误差信号后通过数据采集卡输入到自适应控制器产生次级控制信号，控制信号经作动器作用于简支梁，产生梁的次级振动，与初级振动叠加抵消实现减振功能。误差信号采用PCB加速度传感器，模拟输入模块为四通道NI9215 采集卡，模拟输出模块为NI9263 信号发生卡。功率放大器为南京佛能科技HEAS-5 型功率放大器，作动器和初级振源采用南京航空航天大学振动所研制的HEAS-50型激振器。恒流源使用B﹠WSensingTech的61012 型恒流源。

如图8所示，简支梁在长度方向上被划分为8个单元，9个节点。激振器作用在2号节点和3号节点之间，作动器作用位置为5号节点。参考传感器位于激振器作用点正上方用于测量参考信号，误差信号传感器布放在7号节点，也就是待控制点。

图9为简支梁振动主动控制试验现场图。通过NI9263模块产生一个50Hz、幅值为2 的正弦信号作为干扰力源定频信号,激发梁的初始振动。控制系统工作前，测量带控制点振动响应。打开控制系统，各自适应滤波器的阶数皆取64阶,初值为零,收敛系数uw=0.000 1,us=0.001。采样频率f=1kHz。在控制程序中产生一个零均值,幅值为0.2V随机白噪声信号，加入到主动控制环节的输出控制信号中，通过次级作动器激发次级振动进行振动控制。该随机白噪声信号作为次级通道在线辨识的输入信号，在主动控制环节工作的同时进行次级通道在线辨识。

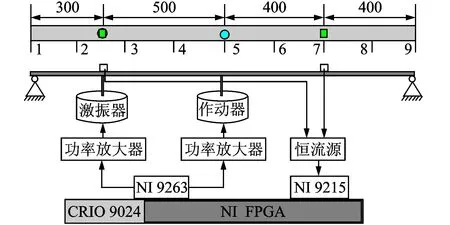
图8 简支梁振动主动控制试验布放简图(单位：mm)Fig.8 The physical diagram of active vibration control(unit:mm)

图9 简支梁振动主动控制试验现场图Fig.9 View of the experimental set-up

图10和图11为整个控制过程中待控制点误差传感器测量的加速度响应时间历程。0～2s为未控状态加速度响应，主动控制器在2s开始工作，待控制点的振动响应被有效地控制下来。未采用附加随机信号控制策略时，控制后振动响应幅值下降了85%。采用笔者提出的附加随机噪声控制策略，控后幅值下降了95%。可见，实施主动控制后悬臂梁测点处的加速度响应得到很好的抑制。从图12可以看出，附加随机噪声对待控制点残余振动量的影响基本消除了。

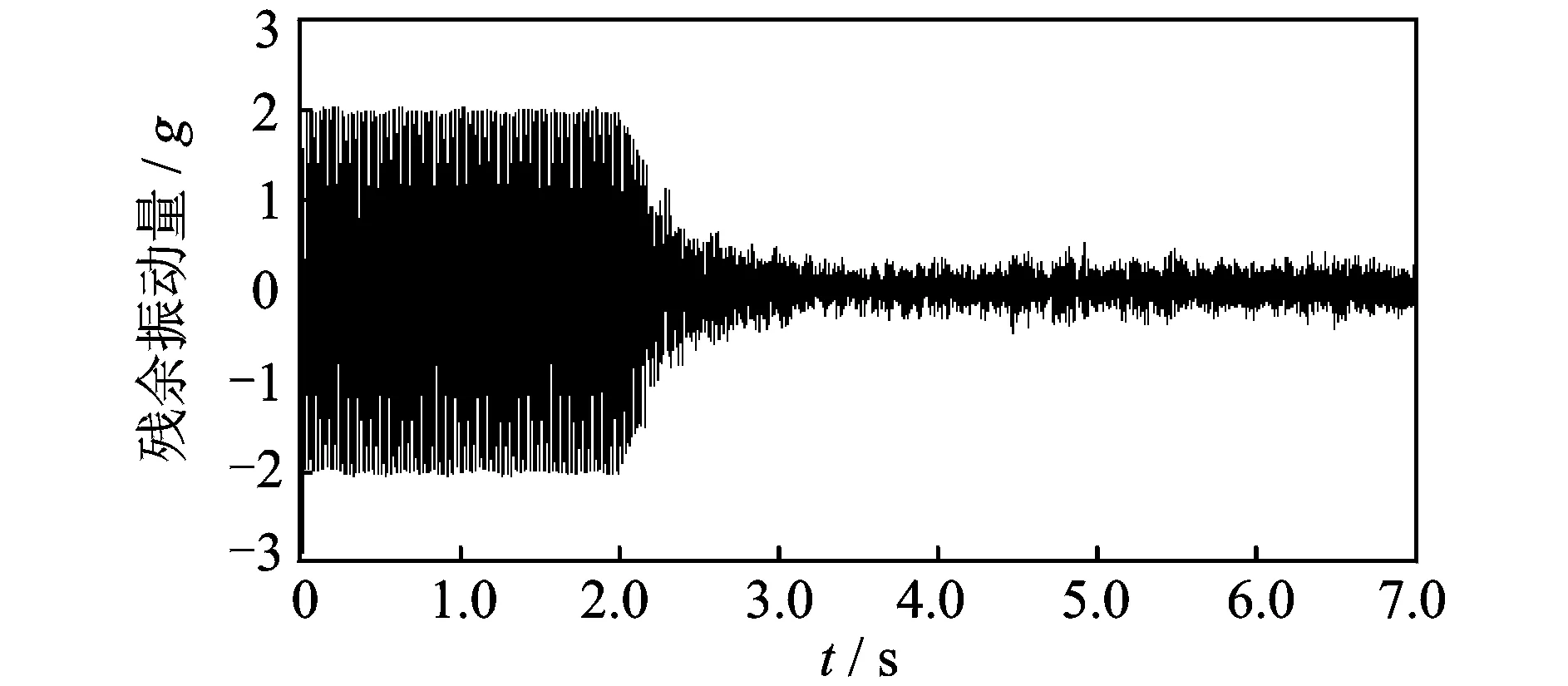
图10 不采用附加噪声控制策略的主动振动控制效果Fig.10 Time history of adaptive vibration contral experiments with no auxiliary noise scheduling

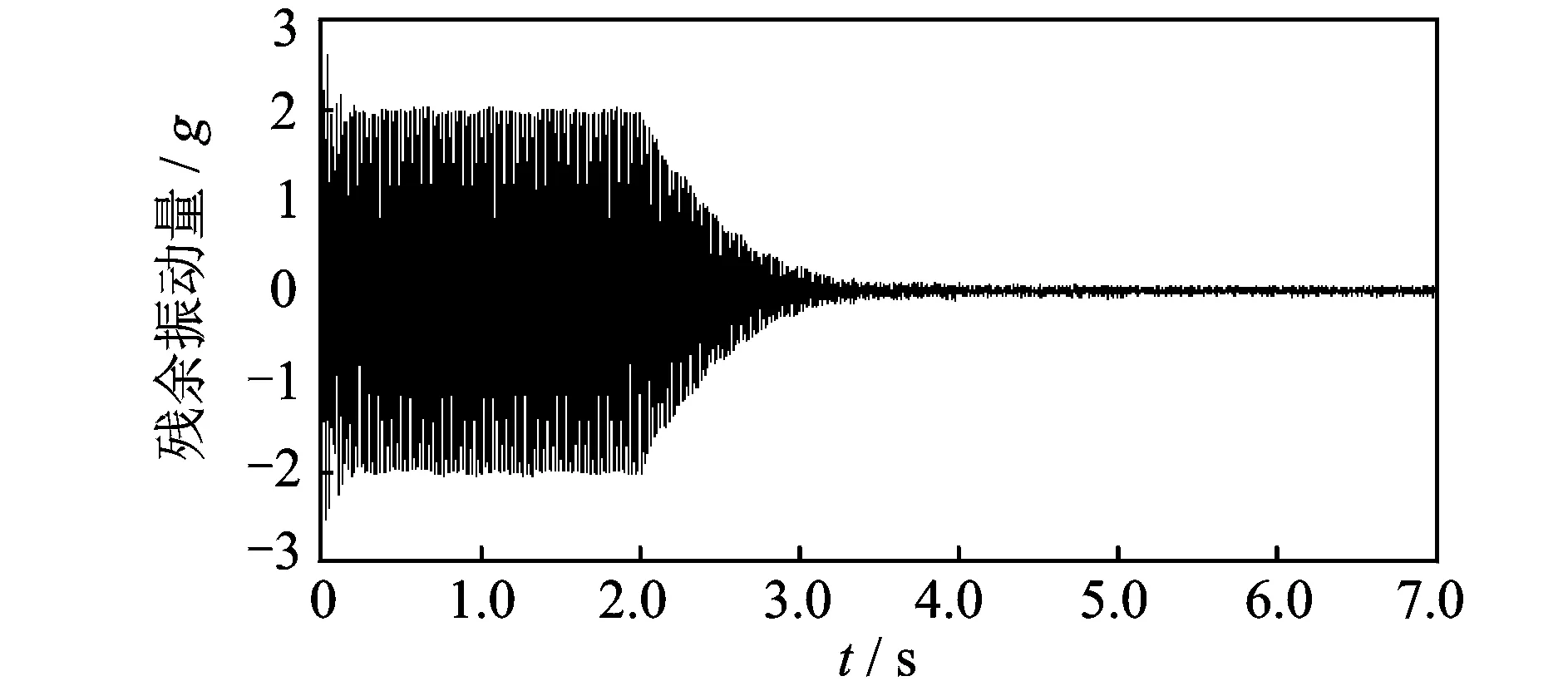
图11 采用附加噪声控制策略的主动振动控制效果Fig.11 Time history of adaptive vibration contral experiments with auxiliary noise scheduling

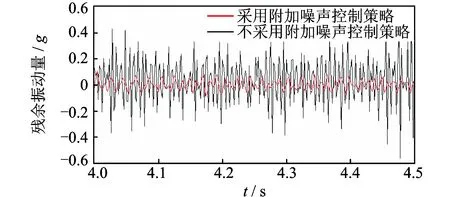
图12 4～4.5 s控制点加速度响应对比Fig.12 Results comparison of 4～4.5s with auxiliary noise scheduling and not

图13为未采用附加随机信号控制策略时，主动控制系统收敛后作动器的输入。这是因为在未采用附加随机信号控制策略时，用次级通道在线辨识算法的附加随机噪声会在次级作动器输入输出信号和控制对象的残余振动量中一直体现出来，所以图13的控制器输入信号为50Hz的简谐信号与附加随机信号叠加。若采用附加随机信号控制策略，当主动控制系统处于稳定状态后，附加的随机噪声幅值会逐渐趋于零，不会在次级作动器输入输出信号和控制对象的残余振动量中体现出来，控制器输入信号则为简谐信号，附加随机噪声对次级作动器控制输入的影响也被消除。

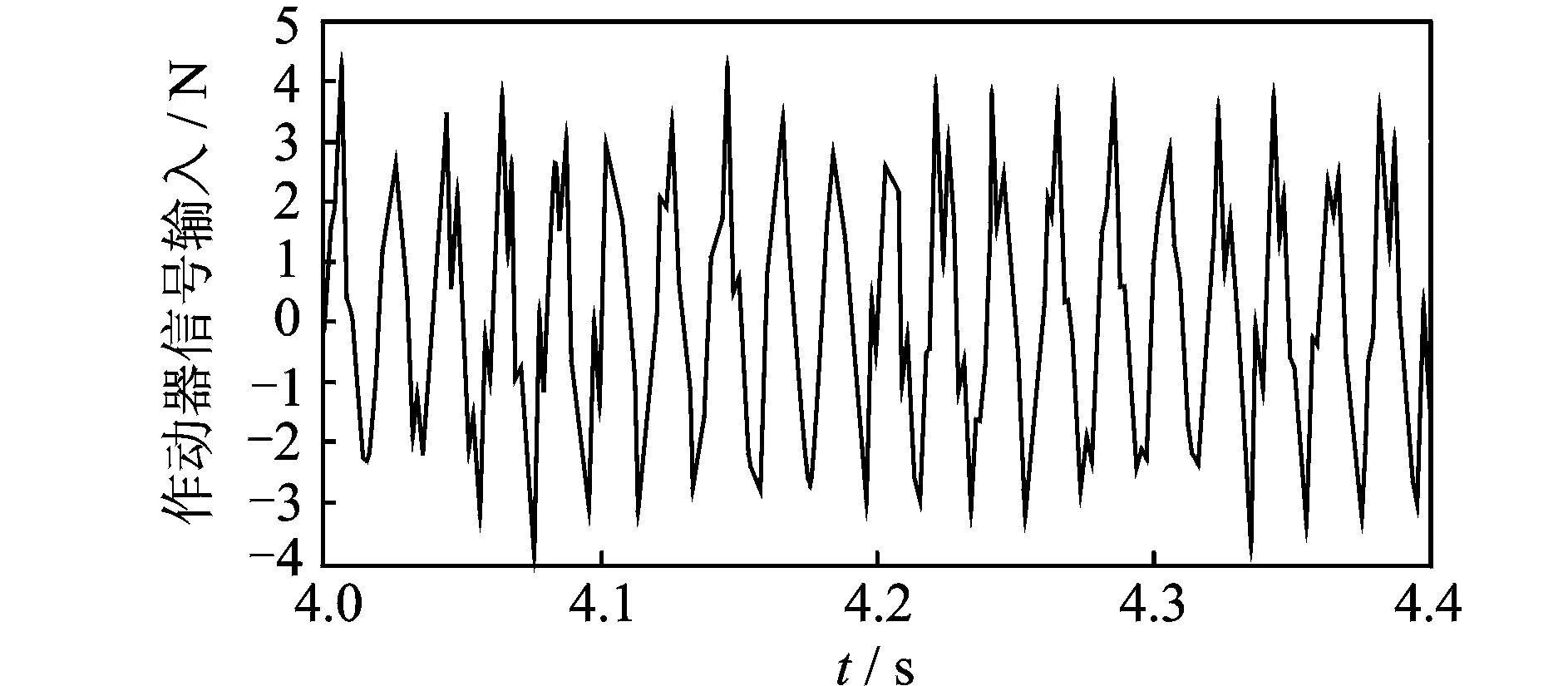
图13 主动控制信号与附加随机信号的叠加Fig.13 The input signal of secondary actuator with no auxiliary noise scheduling

5 结束语

基于最简单的前馈式FXLMS控制模型，提出一种基于改进次级通道在线辨识方法，将其应用到结构自适应振动主动控制中。进过分析，该算法可以消除主动控制环节和次级通道辨识环节相互影响，加快系统的收敛速度，并有效消除附加随机信号对待控制区域残余振动的影响，简化了系统算法的复杂度。以简支梁为控制对象,采用NICRIO实时控制器进行结构振动主动控制的试验。结果表明，该控制系统对简支梁的振动响应有很好的抑制作用,说明这种基于次级通道在线辨识的主动控制方法的有效性。

[1] 吕鑫. 振动主动控制技术的研究及发展[J]. 振动、测试与诊断,1996,16(3):1-7.

Lü Xin. Research and development in actve vibration control technology[J]. Journal of Vibration,Measurement & Diagnosis,1996,16(3):1-7.(in Chinese)

[2] Baumann W T. An adaptive feedback approach to structural vibration suppression[J]. Journal of Sound and Vibration,1997,25(1):121-133.

[3] Alkhatib R, Golnaraghi M F. Active structural vibration control: a review[J].Shock and Vibration Digest,2003,35(5): 367-383.

[4] 浦玉学，张方. 多通道FURLS噪声主动控制算法及仿真[J].国外电子测量技术，2012,31(6): 36-39.

Pu Yuxue,Zhang Fang. Multi-channel FURLS algorithm for active noise control and simulation[J]. Foreign Electronic Measurement Technology,2012,31(6): 36-39.(in Chinese)

[5] 朱晓锦，高志远，黄全振，等.FXLMS算法用于压电柔性结构多通道振动控制[J].振动、测试与诊断,2011,31(2):150-155.

Zhu Xiaojin,Gao Zhiyuan,Huang Quanzhen,et al. Active vibration control for piezoelectric flexible structure using multi-channel FXLMS algorithm[J]. Journal of Vibration,Measurement & Diagnosis,2011,31(2):150-155.(in Chinese)

[6] Snyder S D,Hansen C H. The effect of transfer function estimation errors on the filtered-X LMS algorithms[J]. IEEE Transactions of Signal Process,1994,42(4): 950-953.

[7] Saito N,Sone T. Influence of modeling error on noise reduction performance of active noise control systems using filtered-x LMS algorithm[J]. Journal of the Acoustical Society of Japanese (E),1996,17(4): 195-202.

[8] Eriksson L J,Allie M C. Use of random noise for on-line transducer modeling in an adaptive active attenuation system[J]. The Journal of the Acoustical Society of America,1989,85(2): 797-802.

[9] Bao C,Sas P,Brussel H V. Adaptive active control of noise in 3-Dreverberant enclosures[J]. Journal of Sound and Vibration,1993,161(3):501-504.

[10]Zhang M,Lan H,Ser W. A robust online secondary path modeling method with auxiliary noise power scheduling strategy and norm constraint manipulation[J]. IEEE Transactions of Speech and Audio Processing,2003,11(1): 45-53.

[11]杨铁军，顾仲权，鲁明月，等. 基于误差通道在线辨识的结构振动主动控制系统[J]. 振动与冲击，2004,23(3): 55-59.

Yang Tiejun,Gu Zhongquan,Lu Mingyue,et al. Active control system for structural vibration with online secondary path identification[J]. Journal of Vibration and Shock,2004,23(3): 55-59.(in Chinese)