国外空间计量经济学研究回顾、进展与述评

张可云　杨孟禹



·特稿·

国外空间计量经济学研究回顾、进展与述评

张可云杨孟禹

[摘要]中国未来发展中，可能会大量涉及空间计量经济学建模的应用，如城乡人口流动问题、土地使用方式变化对空间模式的影响等。目前我国一些学者在运用空间计量经济学过程中存在片面选择模型、对最新模型应用较少等诸多问题。根据学科逻辑，回顾国外空间计量经济学研究进展，进一步梳理其理论脉络，对促进空间计量经济学在我国的研究与应用有重要意义。对空间计量经济学的基本概念，空间计量建模过程中的空间效应检验、权重设定、模型估计等方面知识点，结合最新研究进展，总结了空间计量模型应用中应注意的问题，分析了国内空间计量经济学在传播过程中产生的概念不清、方法混淆及误导讹传等现象。最后指出空间计量经济学在发展过程中出现的问题及未来发展方向。

[关键词]空间计量经济学; 空间效应; 空间计量模型； 区域经济研究启示

一引言

Paelinck(1967)[1]，Paelinck和Nijkamp(1975)[2]，Hordijk(1979)[3]等的早期研究，为Paelinck和Klaassen(1979)[4]提出“空间计量经济学”概念与一系列方法奠定了基础，他们系统地论述了空间计量经济学的研究对象、研究内容与基本模型。后来，这些思想被Anselin(1988a[5]，1992[6])，Haining(1990)[7]及Cressie(1991)[8]等进一步发展、拓展，并建立了更有效的空间计量模型，使得空间计量理论逐步完善，但抽象的数学矩阵理论与现实问题研究之间终究存在藩篱，需进一步开展应用性研究。为此，Anselin(1992)[6]，Anselin et al.(1996)[9]与LeSage(1999)[10]等进行了计算方法软件实现研究，这极大地推动了空间计量经济学在区域经济学中的应用。随着空间问题不断显现，新经济地理学派对空间问题的解释(Krugman，1998)[11]再次发展了空间计量经济学。Anselin(2001)[12]刊文指出空间计量经济学存在的理论与应用问题及发展方向，随后Florax et al.(2003)[13]，Anselin et al.(2004)[14]，Arbia(2006)[15]，LeSage和Pace(2009)[16]等对空间计量经济学的理论基础进行了延伸，在应用方面如“经济学帝国主义”般侵入区域经济领域，备受瞩目。空间计量经济学对传统区域问题作出全新解释代表着其应用和研究泛化，此时Elhorst(2010)[17]，Corrado和Fingleton(2012)[18]，LeSage和Pace(2014)[19]等学者对空间计量经济学发展中出现的问题进行了澄清，另一些学者则指出了空间计量经济学的发展方向(Anselin，2010[20]；Gibbons和Overman，2012[21]；Partridge et al.，2012[22])。在此背景下，以Griffith和Paelinck(2011)[23]，Anselin和 Rey(2012)[24],LeSage(2014a)[25],Elhorst(2014a[26]，2014b[27])等为代表的理论表述更规范、理论观点更综合的空间计量经济学文献大量出现。

在梳理国内近五年有关理论研究或应用类文章基础上，发现空间计量经济学理论的研究或应用主要存在以下问题：(1)对空间计量经济学的技术属性和基本原理理解不深，在研究过程中片面地选择模型和设置不符合实际情况的空间权重矩阵；(2)对空间计量经济学相关术语的涵义理解不正确，在查阅文献中发现很多学者对空间计量经济学的空间异质性与区位依赖性、模型分类以及空间动态模型等基本概念不熟悉，甚至出现误用；(3)空间模型选择不够准确和设定的理由不够充分，缺乏理论基础。空间计量经济学涉及多个形式相似而内在机理不同的模型，在具体运用的过程中应根据研究问题的形成机理和所选变量的特征选择合适模型，但是在现有文献中经常发现研究问题的内在本质与最终模型选择并不一致；(4)对空间计量经济学最近发展的直接、间接效应理论认识不足；(5)在经验研究中，模型选择还停留在空间计量经济学的经典模型上，对最新模型应用较少。

导致如上问题的根源在于国内缺乏对空间计量经济学发展脉络、推理逻辑、参数检验与模型选择等方面的系统性文献梳理，也缺乏以学科视角介绍空间计量经济学经典理论与研究进展的文献。空间计量经济学相对于传统计量经济学而言更具现实意义，因为根据地理学第一定律，完全无关的空间数据是不存在的，如“在收益—成本分析中，忽略邻近地区空间溢出效应，就会低估总收益；在中国未来发展过程中，可能会大量涉及空间计量经济学建模的应用，如城乡人口流动问题、土地使用方式的区位依赖问题及土地使用方式变化对空间模式的影响问题等”*James LeSage, R. Kelley Pace. Introduction to Spatial Econometrics[M]. Florida： CRC Press, 2009. 2013年该书被翻译成中文，CRC授权北京大学出版社出版，该句话引自James LeSage于2013年3月写的中文版序。。

根据空间计量经济学的学科逻辑，本文分为六部分：第一部分主要梳理空间计量经济学的发展脉络，简述空间计量经济学主要代表文献的观点及其之间的联系，指出国内研究存在的不足；第二部分分析空间计量经济学的内在本质与基本原理；第三部分主要讨论两大基本概念；第四部分讨论空间计量模型的三个关键问题；第五部分讨论空间计量模型的两个应用；第六部分总结全文，概括本研究对区域经济研究的启示。

二内在本质与基本原理

下面分析空间计量经济学的内在本质与基本原理。

(一)内在本质

传统计量经济学假设空间数据是独立的，这造成其在处理具有相关性的空间数据时出现有偏估计。Anselin(1988a)[5]认为：“一般意义讲，在区域科学内所有经济模型的统计分析都可以被认为是空间计量经济学的范围”，并进一步指出“这种区分实际上与Isard(1956)[28]对空间经济学与非空间经济学分类是相似的。从这个意义上讲，空间相互作用模型的估计、城市密度函数的统计分析以及区域计量经济学模型的应用都可以被认为是空间计量经济学的研究范畴，但是上述分析中的大部分都可以运用传统计量经济学方法实现，因此这种区分实际上是没有意义的”，空间计量经济学与传统计量经济学很难被认为是两个独立的方法。为此，Anselin(1988a)[5]着重从空间数据方面进行区分，他认为“空间计量经济学在区域科学研究中更关注空间数据和模型的特殊性”，这个“特殊性”称为“空间效应(Spatial Effect)”，用“空间依赖性与异质性”进行识别。因此，空间计量经济学与传统计量经济学的区别是很明显的，前者更注重对数据“空间效应(Spatial Effect)”的处理，后者则不涉及数据的空间问题。根据Paelinck和Klaassen(1979)[4]提出的空间计量经济学五大内容，Anselin(1988a)[5]对其进了深化，认为空间计量经济学研究的范围主要包括一系列方法和技术，这些方法和技术依据的是对空间相关性与空间异质性的规范表示，为区域科学模型的适当设定、估计、假设检验和预测提供分析工具。随着区域与城市经济学的发展，空间计量经济学与区域、城市经济学的融合越来越明显，Anselin(2006)[29]将空间计量经济学定义为研究出现在截面观察值和时空观察值中空间问题的计量经济学方法的一个分支。Elhorst(2014b)[27]认为它是处理地理单元(如邮政编码所编地区、城市或者国家等)空间关系的一门计量经济学分支。

Isard(1975)[30]在《区域科学导论》一书中对区域科学的范围作了粗略勾勒，指出：“区域科学作为一门学科，所关心的是采用各种各样的分析性研究和经验式研究相结合的办法对区域内的或空间范围内的社会问题进行细致耐心的研究”。随着区域科学的发展，Anselin(1988a)[5]有过一段经典的论述：“在区域科学研究中，人们通常利用许多有关人类空间行为的理论模型来分析城市与区域面临的种种问题。为了达到这一目的，理论模型往往需要从抽象形式转化为可运算的模型。这意味着需要用规范的数学设定来表述变量关系，需要给出各个变量的含义以确保数据可获得与可计算，同时也需要进行估计、假设检验和预测，这基本上是以统计学方法和计量经济学方法为基础的”。可见，区域科学是抽象的理论，统计学或计量经济学是将其解释问题的过程具体化的工具。

关于空间统计学与空间计量经济学的差异，Anselin(1988a)[5]主要提到两点：第一，空间统计学针对的是数据，而空间计量经济学针对的是模型；第二，空间计量经济学往往是从一个特定的理论或模型出发，并重点研究出现空间效应时的估计、模型设定和检验问题，空间计量经济学一般用于处理区域或城市经济问题，而空间统计学则更关注地理学或生物学的现象本身，与区域科学领域无直接联系。空间统计学是在法国统计学家Matheron(1963)[31]大量理论研究的基础上形成的一门统计学的分支，也称为地理统计学，它是以区域化变量理论为基础，以变异函数为基本工具研究分布在空间中的呈现一定随机性与结构性的自然科学现象。

而空间统计学与经典统计学的区别：一是研究的变量，经典统计学研究的是随机变量，而空间统计学研究的是区域化的变量；二是重复实验性，经典统计学可以重复试验，空间统计学则不能进行重复试验，主要原因是区域之间的数据是不可能重复的；三是数据的相关性。经典统计学每次抽样都是相互独立的，空间统计学使用的数据则具有一定相关性；四是分布特征差异，经典统计学以频率分布图来研究样本分布特征，空间统计不仅要考虑数据本身的特征，还要考虑区域化变量的空间分布特征。因此，经典统计学方法是抽象的，同时忽视了数据的空间特征，而空间统计学则考虑了数据的空间属性，用途较广，地理学、生物学以及人口学等学科都会用到该方法，其研究方法属于一般性研究。

无论是经典统计学还是空间统计学，其本质是对数据信息的挖掘。经典计量经济学则更强调机理分析或模型基础，一般以特定的模型或理论为出发点，在对数据进行必要的说明定义后，用适当的估计方法对模型进行估计或对结论进行检验，其本质是对经济现象进行理论模拟、假设检验和经济预测。空间计量经济学与经典计量经济学本质区别在于，空间计量经济学放弃了经典假设，但考虑了空间相关性与异质性的特征，是区域科学用来分析具体问题的工具，同时也是区域经济学研究实践问题的主要方法论之一，而其他非空间计量方法或统计方法并不考虑该特性。

(二)基本原理

Anselin(1988a)[5]曾经指出，空间计量经济学的观察值都具有时间、空间和时空特性，可以根据其所处的区位、坐标或空间距离进行分类，显然这些观察值与空间单元间的联系有关。Anselin将空间数据的这种特征称为“空间效应”，具体表现为空间依赖性和空间异质性。空间依赖性是指某一点的观测值与其他点观测值之间存在稳定的函数关系。空间依赖性的产生原因有空间扰动性依赖(Nuisance Dependence)与空间实质性依赖(Substantive Dependence)。第一，空间扰动性依赖指对观测值的测算误差引起的空间依赖性，也称空间误差依赖。Anselin(1988a)[5]认为在许多实际研究中，数据往往是在总体层次上收集的，所以研究现象的空间范围与观测值空间单元的范围并不一致，故测算误差时有发生。并且，在各空间单元的边界上这些测算误差往往有溢出现象。因此，一个观测值的误差与其邻近单元的误差有关，这种测算误差的溢出是出现空间依赖性的一个重要原因。从回归的角度看(见图1)，如果存在连续的三个空间单元A、B、C，假设满足非球面相邻关系，由于空间溢出，观测变量满足：Y1=YA+λYB，Y2=YC+(1-λ)YB(Anselin，1988a)[5]，可见参数λ出现在本应该独立的变量Y1、Y2中，同时人为设定的和测算产生的误差引起了空间依赖性。第二，实质性空间依赖是指把空间作为解释人类行为差异的重要因素，也称空间滞后依赖。空间单元的观察值取决于空间上该空间单元以外的观察值，表示为y1=f(y1,y2,…,yN)，N为空间单元个数，同时空间滞后依赖更关注空间单元间的交互作用。空间异质性是指某空间单元观测值与其他空间单元观测值间存在的结构不稳定关系引起的观测值非同质现象，在时间序列和横截面数据的回归中，一般可以表示为*Anselin. Spatial Econometrics：Methods and Models[M]. Kluwer Academic Publishers, 1988a:13.：yit=fit(xit,βit,εit)，i为空间单元观测值，t为时间周期，fit是关于自变量xit、参数向量βit在误差εit条件下与因变量yit的具体时空函数关系。实际上传统计量经济学中已经涉及到一些对于异质性的处理方法，如在面板数据中，通常需要在固定效应与随机效应模型间做出选择。此外根据LeSage 和 Pace(2009)[16]观点，空间异质性实际上可转化为空间误差依赖或空间杜宾模型形式。

图1　空间依赖性与集聚

资料来源：Anselin.SpatialEconometrics：MethodsandModels[M]. Kluwer Academic Publishers, 1988a：12.

我们认为，在运用空间计量经济学模型时，关于模型的产生或选择过程，不能过多依赖于假设检验，而应把假设检验作为辅助手段。事实上根据空间相关性与空间异质性，并结合数据特征与经济理论，可以做出一些基本判断。

对于空间计量经济学模型产生基础的研究，到目前为止LeSage和Pace(2009)[16]的观点比较全面，同时Anselin(1988a)[5]将空间数据分为空间依赖性与空间异质性这两类进行研究，把空间计量经济学产生的基础概括为更细致的五个方面：

第一，时间依赖性。指经济行为人当期的决策经常受其他行为人前期行为的影响，例如，本地政府可能在观察到邻近地区前期的税率滞后现象而来制定当地的税率。

第二，遗漏变量。在研究中，再好的模型也不可能穷尽所有对因变量可能产生影响的因素，尤其是不可观测变量，它在模型中往往难以捕捉。

第三，空间异质性。如果把回归方程的截距看作是空间结构的随机效应向量，那么可以根据截距是否与自变量x相关而对空间异质性进行建模；也可转化为空间误差来处理。

第四，外部性。指某一空间经济事件对邻近地区的影响。

第五，模型的不确定性。由于在实践中往往面临对模型的选择、常规参数和解释变量的设定等不确定因素，这些不确定性因素也就造成了模型数据生成过程中的不确定性，从而使得回归模型中含有因变量与自变量的空间滞后因子。

三空间效应与空间权重

空间效应与空间权重是空间计量经济学的两大基本概念。

(一)空间效应

根据Anselin(1988a)[5]的观点，空间效应是空间计量经济学成为一个独立学科的基础。空间计量经济学中的空间效应(Spatial Effects)是指空间相关性与空间异质性。对于空间溢出效应，Anselin只在解释空间数据相关性时提到，认为空间溢出是产生空间相关性的原因之一，对于空间溢出效应，却没有详细地讨论。直到LeSage和Pace(2009)[16]将空间溢出效应(Spatial Spillover Effects)作为空间计量经济学模型估计的核心内容之一，并认为“空间溢出效应是指单个空间单元某个变量变化所导致的空间影响，这是区别空间计量经济学与许多空间统计模型的关键”。因此空间效应表示空间数据存在的特征和形态，同时空间溢出是产生空间效应的原因之一，空间溢出效应是单个区域某个变量变动对其他区域影响的度量，也是空间计量模型效应估计过程中的特色之处。

与之相关，在空间计量估计中还有一个关键的概念是“反馈效应”，它表示本地区直接作用于邻近地区后又传回本地区的结果，该值的正或负表示反馈的正或负。关于其作用机制的研究文献不多，LeSage和Pace(2009)[16]将反馈效应等同于SDM模型中X的一般估计结果与直接、间接效应理论采用混合解析海塞形式的模拟参数而产生的估计值之差。经验研究表明，以上二值的差异很小且无实际的经济意义，遗憾的是，他们并没有从理论上证明这种反馈效应估计方法的有效性，此后文献再无相关讨论。LeSage和Pace(2009)[16]经验研究表明，边际直接效应显示出较小的反馈效应，同时随着空间权重阶数的增加，反馈效应衰退较快。当然，该研究也只是针对特定空间，结论是否具有一般性，有待进一步考察。另一个关键词是“空间分割(Spatial Partitioning)”，当前国内区域学界的定义并不规范，一般文献将其理解为“市场分割(Market Fragmentation)”。根据LeSage和Pace(2009)[16]的观点，空间计量经济学一般用空间权重的阶数来表达空间边界，空间边界越大，空间权重矩阵的阶数越高，直接效应或间接效应的边际变动随之衰减，可以用对应于空间权重矩阵阶数下的直接效应或间接效应的T检验值的显著性来判定空间最大边界，由此形成的空间现象称为“空间分割(Spatial Partitioning)”，同时空间分割可以用来推断一个区域某个空间单元的经济变量的空间作用范围，主要原因在于区域运行系统之间缺乏良性互动(空间溢出效应)而形成的相互分割的经济运行空间。

通过分析国内文献，我们发现将“空间效应”的涵义等同于“空间影响”或“空间作用”是一个普遍现象，此外有的学者还将空间效应与空间溢出效应混淆。当然在非空间计量经济学中，也有“空间效应”一词，将其解释为“空间影响”或“空间作用”是合理的，上述误解很可能就是受此影响。关于“空间效应”也许是一个有争议的话题，但我们认为至少在运用空间计量经济学方法时，应注意到，空间效应是一个特指空间相关性与空间异质性的术语。不妨借鉴LeSage和Pace(2009)[16]提出的直接、间接效用理论，该理论已不再提及“空间效应”一词，而是将模型中变量参数解释为“累积效应(Cumulative Effects)”，该效应由直接效应和间接效应(空间溢出效应)组成，这在很大程度上避免了上述误解或争议。最后一点是，很多学者将空间滞后变量的估计系数作为该变量的“空间溢出效应”，这在LeSage和Pace(2009)[16]的纠正及Elhorst(2010)[17]的深化之前是国内外计量经济学运用的通病，空间滞后变量系数与间接效用(衡量了空间溢出效应)之间是有差异的，然而前者很容易造成误判。

(二)空间权重

空间计量经济学在应用中首先面临的问题是如何在模型中表达空间效应。最简单的方法是运用空间邻接矩阵。这可追溯至Moran(1947)[32]和Geary(1954)[33]的研究，他们构建了基于0、1的二进制空间邻接矩阵。根据他们的观点，对于邻接关系的定义主要有以下几种方式：第一，空间单元共用一条边(Common Edge)，依据国际象棋的规则，习惯上将其命名为“车步(Rook)”规则；第二，空间单元共用一个顶点(Common Vertex)，称为“后步(Queen)”规则；第三，由于上述规则只能适用于空间单元“地位等级相似”的情况，当在研究具有等级特征的城市系统时，往往面对的是规则区域与不规则区域交叉的情境，此时最适合“半径(Radius)”规则。半径规则是以一定的空间距离为邻界点，落在距离之内的视为邻接关系。此外考虑到空间溢出所产生的空间效应随地理距离的增加而逐渐衰减的现象，可根据衰减的速度设定空间权重矩阵。在设定空间权重矩阵过程中，一般用地理距离的倒数表示空间单元的邻接关系，建立反距离矩阵；第四，以上几点只考虑了空间单元都是“点”的情况，如果考虑拓扑结构，即把空间单元的“点”换成“区域地图”，就会出现一些较小的地理单元，这些较小的地理单元有很多邻近单元，而较大的地理单元则可能很少有邻近单元，这就造成邻近结构的不平衡，从而产生了误差。一般通过递归的方法来计算邻接关系，当任意空间单元一阶相邻于K-1个相邻的空间单元且没有更小的空间单元存在时，定义K阶相邻，根据相邻的关系设定，可产生基于“车步”规则和“后步”规则的K阶相邻关系。一个经典的空间权重矩阵是由Cliff 和Ord(1973[34]，1981[35])构建的Cliff-Ord矩阵，它将空间单元间的距离与共同边界的长度考虑在内。在区域科学的应用中，空间权重矩阵常采取距离和邻接矩阵相结合的方式进行设定(Anselin，1988a)[5]，对于空间权重的本质，Anselin(1980)[36]最先指出，应该将空间依赖性与空间权重有机结合起来，尤其是与空间交互理论相关的一些概念。与空间计量经济学建模动机相一致，空间权重矩阵应该是空间相关性的概念化，而不是空间相关模式的即时描述。

由于邻接权重矩阵的假定是空间相互作用仅仅取决于区域空间相邻，也认为所有相邻空间单元的空间相互作用程度是一样的，其对区域结构的变化并不敏感。而空间距离权重矩阵在一定程度上反映了空间溢出的衰减特征。但有学者认为地理距离并不是产生空间溢出的唯一因素，林光平等(2005)[37]和Beck et al.(2006)[38]分别用非空间因素的经济总量和区域贸易流来定义空间权重矩阵，此后该类方法在国内迅速发展。

本文在分析文献的过程中发现一个有趣的现象，对于非空间概念定义的权重矩阵，如经济权重矩阵，国内文献的使用频率比国外要高很多。而经济权重是区域某个经济变量的绝对值差的倒数，学者们为什么选择经济权重？原因可能是：

第一，针对特定问题，如大城市对周边小城镇的影响，地理权重矩阵不能完全体现区域间的相互作用，而经济变量有可能成为空间溢出的主要因素。

第二，社会学家们通常所说的“社会距离”，并不是指实际的地理区位。例如，在网络世界中，因为可以共享信息，两个地理距离很远的人也可能很近(Watts 和 Strogatz，1998)[39]。对此，LeSage和Pace(2009)[16]研究认为空间计量模型中因变量空间滞后的偏导数，度量的是区域系统从一个稳定均衡到另一个稳定均衡的变动，而用空间概念定义的权重矩阵不会随时间变动，通常用模型参数估计来推测区域特征变量的变动，但它会得出比较静态的结果；而非空间权重矩阵由于其随着时间变动发生动态变化，从而能够反映全局空间溢出，能解释空间溢出存在的问题。因此在应用中要特别注意，用非空间权重矩阵估计出的系数具有解释陷阱(LeSage，2014b)[40]。

从空间计量经济学产生的基础来看，无论是空间依赖性还是空间异质性，其背后都有数据间的非独立关系。既然要研究数据间的这种关系——空间溢出效应，那么定义不随时间变动的空间权重矩阵来表示既存的空间关系是合意的，这里强调的是“溢出关系”的研究。非空间权重矩阵，如社会距离、经济距离，将随时间变动的经济状态量作为“空间关系”来表示，空间溢出荡然无存，将社会学上的虚拟距离概念套入空间计量经济学上，属于典型的社会学“风格帝国主义(Imperialism of Style)”*风格帝国主义指将一个学科的研究风格，如研究方法与标准强加于其他学科。可见文献：Mäki, U., Marchionni, C.. Is Geographical Economics Imperializing Economic Geography?[J]. Journal of Economic Geography, 2011, 11(4): 645-665.。从非空间权重的逻辑上分析，经济距离权重认为两个区域经济总量越接近，空间溢出效应越强，这继承了反距离空间权重的思维逻辑，而经济联系的复杂性必然使得这种矩阵不准确。然而，经济总量差异大的两个区域的空间溢出一定比差异较小时的空间溢出小吗？答案是不一定的。原因是两个要素禀赋不同的区域，可能因横向的产业间分工而产生关联，二者经济量趋同；也可能由于纵向的产业内分工产生关联，此时二者经济量趋异。因此在应用非空间权重矩阵时应持有谨慎态度。

针对以上空间权重矩阵的设定问题，LeSage(2014b)[40], LeSage和Pace(2014)[19]指出，已有文献存在一个错误认识，即空间回归模型的估计值与推导值对权重矩阵的设定是敏感的，但通过遵循他们提出的空间权重构建的几个简单原则，就可以保证构造的模型估计值稳健。空间权重构建的原则是要尽量设定简单的空间权重矩阵，可以通过以下几个方面实现：(1)稀疏的邻接矩阵(矩阵中绝大多数元素为0)最为有效。(2)衰减参数的识别问题，通常距离衰减被作为一个参数来估计，但当空间依赖参数为0时，并没有明确定义相应的衰减参数值，这可能使似然函数产生“断点”。此外，由于不同权重矩阵下的估计值与推论类似，用统计方法检验衰减参数的不同值可能会遇到障碍。(3)除非能够对引入的矩阵进行明确解释，否则应避免在同一个估计模型中出现不同的空间权重矩阵。(4)注意用非空间概念来定义空间权重矩阵在估计时对空间溢出效应的干扰陷阱。

四空间效应检验、空间模型选择与空间模型估计

空间效应检验、空间模型选择与空间模型估计是空间计量经济学建模的三个关键问题。

(一)空间效应检验

对空间效应的检验，最早可追溯到Cliff和Ord(1972)[35]，Hordijk(1974)[41]的研究，他们将Moran’I指数应用于截面数据的空间自回归检验上，后来这种方法被广泛应用于空间计量模型中空间依赖性的识别上。目前对空间效应的检验一共有8种方法，分别是，莫兰指数法Moran’I、空间误差依赖的拉格朗日乘数检验LM-ERR(Burridge，1980)[42]、空间误差依赖的K-R检验(Kelejian 和 Robinson，1992)[43]、空间滞后依赖的空间误差检验LM-EL(Bera和Yoon，1992)[44]、二阶空间误差依赖的拉格朗日乘数检验LM-ERR(2)(Anelin，1994)[45]、空间自回归移动平均的拉格朗日检验SARMA(Anselin，1994)[45]、空间滞后依赖性的拉格朗日检验LM-LAG(Anselin，1988b)[46]和基于空间误差依赖性存在稳健性的空间滞后依赖性检验LM-LE(Bera 和Yoon，1992)[44]。国内有文献将这一系列检验方法归结为空间效应识别、检验与空间自回归、空间误差模型和空间杜宾模型中关键系数是否为0两种检验方法(张志强，2014)[47]。实际上，根据空间效应中空间相关性的产生机理，可直接将这些检验方法分为两类：空间误差依赖性检验和空间滞后依赖性检验，以上8种检验方法的原假设都是无空间依赖性，而通常的备择假设是空间依赖性满足空间自回归移动平均或SARMA过程(Anselin和Florax，1995)[48]。

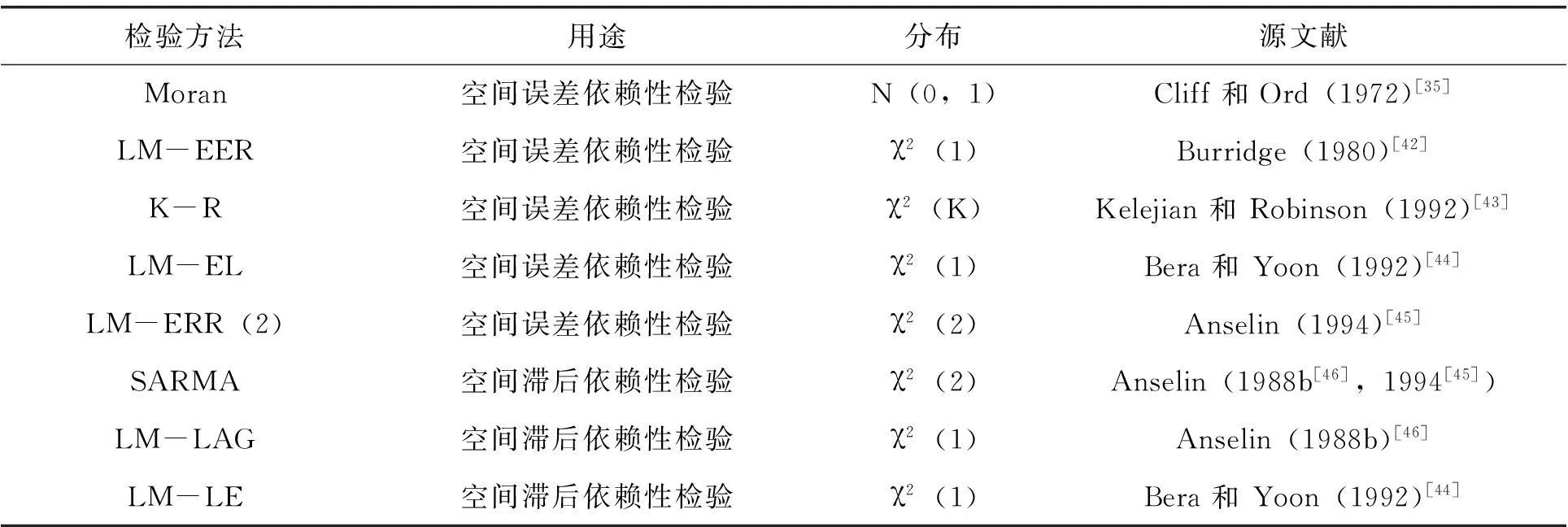
表1　空间计量模型中基于经典最小二乘回归的空间依赖性检验法

资料来源：Anselin 和 Florax(1995)[48], Anselin et al.(2004)[14], Elhorst(2014b)[27]。

目前国内外较为一致的方法是采用Moran’I指数、LM-EER、LM-LAG及空间滞后稳健性R-LMlag、空间误差稳健性R-LMEER相结合的检验。

(二)空间模型选择

国内空间计量经济学的理论研究严重滞后于国外，虽有少量文章(孙洋，2009[49]；陈青青等，2014[50])，但绝大多数在讨论模型选择时只停留在数据分析层面，而缺乏深入的理论研究。实际上，前文所述的空间模型产生的五大动因也是选择空间计量模型的五大原则。除五大原则外，在选择空间计量模型时不仅要考虑具体设定形式，同时也要考虑自变量和因变量的理论关系，这就需要进行深入的区域经济学理论分析。

空间自回归模型和空间误差模型是空间计量经济学的两大基础模型，空间自回归模型认为一个空间单元的因变量会通过空间传导机制影响其他空间单元的因变量；而空间误差模型则认为空间外溢性或相互作用是随机冲击的结果。空间自回归(SAR)模型y=ρWy+βX+u，在有的书籍中也称为空间滞后模型，因为在方程中引入了一个表示空间滞后的矩阵W，ρ是待估参数，用于讨论表征空间单元之间是否存在显著的空间相关性。在模型中，我们应该注意这种相关性是指在给定“空间邻接性”下所有“相邻”单元对于本单元存在的一种被平均化了的外部影响的现象。

与SAR模型的空间相关性相比较而言，空间误差模型(SEM)主要在空间滞后项上存在不同，SEM完全去掉空间滞后项，将其表现在误差项上。如表达式为：y=βX+u,u=λWu，相邻单元与本单元之间的关系不仅表现在因变量y上，而且更有可能表现在一些未被观测或遗漏的变量上。作为更一般的空间计量模型形式，空间杜宾模型(SDM)兼具以上两个模型的特点，同时它引入了因变量与自变量的空间滞后变量，空间滞后变量的优点在于一方面解决了建模过程中的遗漏变量问题，另一方面对空间异质性与不确定性的处理更为有效(LeSage和Pace，2009)[16]。

空间自回归模型除了上述模型外，还有SAC模型与SARMA模型。SAC模型考虑了因变量与扰动项的空间相关性，而SARMA模型将局部空间移动平均与全局空间自回归过程相结合，二者的区别在于扰动项数据生成过程的差异；如果考虑到模型空间的外部性，即一个空间单元的自变量以及邻近单元的自变量会对因变量产生影响，该模型可称为X的空间滞后模型(SLX)。

基于以上各线性模型之间的关系，Elhorst(2014b)[27]阐述了从空间模型到OLS模型的特殊到一般模型的过程。在演变过程中LeSage和Pace(2009)[16]曾对几个经典的空间计量模型进行比较研究，他们假设原始数据分别满足SEM、SAR、SDM、SAC数据生成过程，对可能误设的模型及造成的估计结果进行了分析，具体见表2。

表2　几个典型的空间计量模型设定的比较

资料来源：作者参考LeSage和Pace(2009)[16]的研究整理。

LeSage和Pace(2009)[16]基于不同加权矩阵构造模型，然后运用对数似然函数值的贝叶斯选择法进行检验。贝叶斯方法由Zellner(1971)[51]提出，其提出的目的在于对不同模型进行比较。首先是设定每个模型的先验概率(LeSage，2014a)[25]，如果模型的数量为n，那么先验概率为1/n；其次利用回归参数的先验分布；最后计算后验模型概率，以此来判断不同回归模型与先验信息的一致性。第二个问题是如何对含有不同变量的空间模型进行比较，在模型建立过程中为了克服遗漏变量的偏误，总是倾向于考虑将尽量多的变量纳入模型，但这也会降低估计精度，不同变量的空间模型比较的目的正是这样一种权衡。对此，Madigan和York(1995)[52]提出的马尔科夫链蒙特卡罗模型组成方法(MC3)被广泛应用，同时LeSage和Pace(2009)[16]也指出了该方法的不足：忽略了来自模型内部的空间权重设定差异与参数不同带来的不确定性问题。

在空间建模过程中，上述两种方法对选择空间权重类型与解释变量的不确定性问题提供了思路，其中MC3法实际上是基于特定的空间权重条件。只要给定基于不同空间矩阵的一系列模型，就可以计算出每个模型的后验模型概率，而具备最高后验概率的模型即为最优模型。然而我们发现，在空间计量模型的实际运用中，很少有论文运用上述方法对模型的空间权重矩阵选择与模型选择过程做严谨地讨论，这也成为了那些非空间计量学者批评空间计量经济学主观性的主要论点。但实际上，无论是传统的非空间计量经济学还是空间计量经济学，模型设定都不可能做到完全客观。而近年来，空间计量经济学的有关理论正在逐渐完善，但问题的关键是对这些理论的应用性研究不足，尽管LeSage、Elhorst分别编写出相应的实现程序，但限制空间计量经济学发展的主因仍是缺乏计算应用程序研究。

LeSage(2014b)[40]接着指出，以往文献过分重视SAC模型，因为其在理论上符合经济计量的要求。实际研究中完全可以忽视这个模型的假设，因为其在应用中存在许多限定。事实上，一般认为只有两种模型设定是值得区域科学研究者考虑的，即SDM与空间杜宾误差模型(SDEM)。这能够有效地节约选择合适模型的时间成本。在建模过程中，如果能在理论上证明存在唯一的设定，可能是地区外溢设定，或者是全局外溢设定，那么研究的问题会进一步得以简化。若存在关于这两种设定哪一个更合适这一问题，贝叶斯模型比较法能够提供精确的推断。这些模型比较方法可运用于简单截面问题或者静态与动态面板数据问题。然而，这些方法尚未能够运用于probit和tobit模型之中。

(三)空间模型估计

空间回归模型揭示出变量间、空间单元间复杂的依赖关系。针对此前学者对空间溢出效应估计的不足或偏误，LeSage和Pace(2009)[16]提出了“直接与间接效应理论”或“描述性标量度量法”。对此，Elhorst(2010)[17]支持将间接效应作为估计空间溢出是否存在的重要基础，以及用贝叶斯后验概率模型确定最适合的空间权重矩阵，并对其贡献倍加赞赏。该理论认为应该用直接效应、间接效应(空间溢出效应)和累积效应来代替传统空间计量经济学上对空间溢出参数的错误解释。直接效应是指任何一个区域的相关变量的改变对该地区本身的影响，而间接效应是空间单元间的相互影响，也称为空间溢出效应。OLS和SEM模型由于不包括因变量的空间滞后项，所以不存在间接效应，它们估计出的参数只能根据传统回归的偏导数观点来解释其经济含义。针对SEM模型忽视空间溢出效应估计的缺陷，LeSage和Pace(2009)[16]提出了空间杜宾误差模型(SDEM)，该模型具备估计间接效应的能力。除此之外，SAR、SLX、SDEM、SDM和一般嵌套空间模型(GNS)等都可以估计直接效应或间接效应。表3是几个典型空间模型(截面)估计效应的表达式。

表3　不同静态空间截面模型的直接效应与间接效应

资料来源：Elhorst(2014b)[27]。

空间计量经济学的估计方法主要包括：最大似然估计法ML(Ord，1975)[53]、准最大似然法QML(Lee，2004)[54]、工具变量法IV(Anselin，1988a)[5]、广义矩估计法GMM(Kelejian和Prucha，1998)[55]和贝叶斯法 MCMC(LeSage，1997)[56]。根据数据结构的差异，空间计量模型有三种不同的估计模型，分别是横截面模型估计、空间面板模型估计和动态空间面板模型估计。在截面数据中，QML和IV/GMM的优点是模型的误差扰动项不依赖于正态分布的假设，Liu和Lee(2013)[57]的研究表明IV/GMM法在估计线性空间依赖性模型或处理模型内生性方面具有很强的优势；对于空间面板模型的估计方法，LeSage和pace(2009)[16]，Elhorst(2014b)[27]主张采用ML和贝叶斯法，但是对于空间面板下的不同模型估计，设定有所差异。

Elhorst(2014b)[27]对近几年出现的动态面板理论进行了综合分析，并做了系统研究。按照他的观点，广义的动态空间面板模型表达式如式(1)，根据各变量前参数的取值不同，可将其演变为两种典型的非空间动态面板模型：第一种情况为σ=η=0，β2=β4=0，称为非空间动态面板模型；第二种情况为τ=η=0，β3=β4=0，称为空间非动态面板模型。除以上两种情况的模型外，其余模型均称为空间动态面板模型。严格来讲，动态空间面板模型可分为7种：第一种是在误差项中混合了时间和空间的模型，表达为εt-1+Wεt；第二种模型通过设定因变量的一阶滞后变量和空间随机误差项为方程的解释变量，将时间和空间有效地混合，其表达为Yt-1+Wεt；第三种模型为空间杜宾模型的动态扩展，表达为τYt-1+σWYt+ηWYt-1+β1Xt+β2WXt；在第三种模型的基础上，Yu et al.(2008)[58]与Lee和Yu(2010)[59]提出了添加β2=0的限制条件成为第四种模型；第五种模型是在第三种模型的基础上添加σ=0条件，该模型由LeSage和Pace(2009)[16]提出；第六种模型是添加限制条件η=-τσ，由Parent和LeSage(2010[60]，2011[61])提出；第七种模型是添加限制条件η=0，由Elhorst(2010)[17]，Franzese和Hays(2007)[62]，Kukenova和Monteiro(2009)[63]等提出。

Yt=τYt-1+δWYt+ηWYt-1+Xtβ1+WXtβ2+Xt-1β3+WXt-1β4+Ztπ+vt

vt=ρvt-1+λWvt+u+ξtN+εt

u=κWu+ξ

(1)

以上7个空间动态模型区别在于(Elhorst，2014b)[27]：静态空间杜宾模型仅能估计长期直接效应和长期间接效应，而无法估计短期效应；时间或空间的误差项滞后模型仅能估计长期直接效应，无法估计间接效应；动态空间误差模型仅能估计长短期直接效应，无法估计间接效应；动态空间杜宾模型能对长短期的直接效应与间接效应进行有效估计；对于第四种模型，虽能对长短期的直接效应与间接效应进行有效估计，但要求每一个解释变量的间接效应与直接效应的比是相同的；第五种模型虽能对长短期的直接效应与间接效应进行估计，但不能估计短期全域溢出效应；第六种模型同样能估计出长短期的直接效应与间接效应，但其要求直接效应与间接效应之比是常数；第七种模型能对长短期的直接效应与间接效应进行有效估计，并且没有其他要求。由于空间动态面板模型的形式多样化，在实证研究中具体采用哪一种形式是最优的，还有待于后续研究。

动态空间面板模型的估计方法一般是基于ML或QML、IV/GMM或MCMC发展而来。Elhorst(2014b)[27]认为这些方法主要存在如下问题：第一，因变量空间滞后项的系数估计偏差误差问题，而到目前为止，没有一种方法能有效解决此问题；第二，时间样本T很小时模型估计的性能问题，为此，用外生的变量代替初步观察到的内生性变量的处理方法或许是有用的。第三，不是所有的模型都能解释内生变量与因变量滞后变量的差异；第四，把空间动态面板模型的平稳性条件添加到模型中的目标不能轻易实现。此外，Baltagi和Fingleton(2014)[64]通过蒙特卡罗模型法比较了空间与非空间GMM估计的性能，并进行了经验验证，认为GMM估计法在动态空间面板估计中值得推广。

五在区域经济研究及其他领域的应用

(一)针对区域经济问题的应用

空间计量经济学在区域经济学研究中的用途非常广泛，这里不再重复前文所述的空间计量经典模型。从Anselin(1988b[46]，2006[29])对空间计量经济学定义的演变和Elhorst(2014b)[27]最近的定义可以看出，空间计量经济学在区域经济学中的作用越来越重要，且逐步融入实际应用研究领域。由于地区间的交互作用直接与地区规模成正比，所以在一般经济学意义上，将引力模型称为空间相互作用模型(Sen和Smish，1995)[65]。空间相互作用模型与一般空间计量模型的区别在于它把距离作为解释变量，其可以消除区域间来源地—目的地流量中的空间依赖的影响。LeSage和Pace(2008)[66]指出来源地—目的地之间的流量在本质上具有空间特性，因此，假设这些流量相互独立是不合适的。为此他们对传统的引力模型进行扩展，纳入了被解释变量的空间滞后项，这对区域经济学中研究区际贸易、运输经济、人口迁移、商品流动、网络信息交流、上班通勤等领域具有里程碑式的应用价值。近年来，复杂的地形对交通网络产生影响，户口政策的变动、轰轰烈烈的高铁网络建设深刻地影响着中国区域经济格局。对于研究者来讲，与之对应的是研究中建模的困难，对此我们认为可以借鉴空间相互作用扩展模型(LeSage和Polasek，2008)[67]。该模型利用区域的交通网络结构先验非样本知识，对空间权重矩阵进行了调整，从而改善模型。由于一般空间权重矩阵的假设是每个空间单元的变量信息是均质的，而与受地形限制的交通网络发展现实是不一致的，同一条交通线有的地方交通网络发达，有的地方比较落后，造成了空间上来源地—目的地间的流量差异。而上述方法正是用来解决这一问题的，同时也应用数理方法对一般空间权重矩阵进行了修正，对于该模型的估计，他们提出矩量矩阵方法，最后可直接用于最大似然估计和贝叶斯估计。

矩阵指数空间模型(MESS)对空间自回归模型(SAR)进行了改进。普通SAR模型中的自回归过程是几何衰减的，MESS正是将这种几何衰减的方式改进为指数衰减方式，而这种方法无论在指数求逆，还是微积分上都具有很大便利性，所以其理论基础更为丰满，估计效率更高(LeSage和Pace，2009)[16]。在空间中经常存在这样一些现象：空间单元间变量观测值的相互影响路径并不单一，而是存在很多路径。因而，很有可能当某个空间单元的变量观测值变化时，间接地影响其他空间单元的观测值。如果出现较小的空间高阶依赖，虽然单个路径上看很小，但累积效应有可能对空间格局产生影响，也会对观察值产生影响。另一方面，由于实际的空间环境并非像平原一般井然有序，例如中国东中西部地区空间环境差异很大，且受边界、河流、行政区划及其他空间界限的影响，更可能引起空间的多重反馈与高阶依赖。由MESS扩展而来的分数差分法，能对上述问题进行建模分析。LeSage和Pace(2009)[16]研究认为，允许高阶依赖性存在的分数差分法更偏向于建立空间邻接权重矩阵，而基于移动平均的不允许高阶依赖存在的方法(如SAR)，更倾向于建立最近邻的矩阵。这在研究中国不同空间系统下的区域问题具有重要意义，遗憾的是目前国内这方面的经验研究文章较少。

最后一种模型是针对性最强的模型，空间计量模型的空间依赖产生过程还可以是二元选择行为，受限因变量空间模型即为对该种空间依赖产生方式的建模。典型的例子是在同一条交通线贯穿下的不同空间单元，由于相邻起点乘客面临着类似出行交通工具的选择，且在相邻的不同的空间单元，人们面临的公共交通资源同样充分或同样不足，很容易形成空间依赖。实际上，类似研究早就存在， Holloway et al.(2002)[68]研究表明孟加拉国用于水稻种植的土地由农业用地转为非农业用地的决策存在空间依赖性。为此对该模型进行估计，以贝叶斯法为例，将观测值0、1看成是无法观测的潜在效用代理变量，并将其转换为连续因变量贝叶斯法所使用的条件分布进行抽样，从而对模型的参数进行估计(LeSage和Pace，2009)[16]。

由于中国正处于经济社会变革与区域经济发展空间格局变动的关键时期，随着市场经济体制机制不断完善，要素流、信息流与资金流在区域间流动愈发明显，空间相互作用模型在这方面将具有很大的应用价值。MESS改善了SAR等一些模型的不足，将几何级衰减方式替换为指数衰减方式，在模型估计过程汇总具有理论和应用上的优势，尤其是考虑了空间交通网络、信息流、资金流差异的分析，这将进一步推动区域经济领域的空间计量经验研究，而因变量空间模型在解释区域经济主体的行为模式上具有重要作用。

(二)对创新等其他领域的应用

空间与创新的关系是空间经济学的最后领域(Marshall，1920)[69]。从目前的理论发展动向上看，空间计量经济学也如此。第一，知识外部影响空间有界性是新地理增长理论(New Geography and Growth Theories)解释空间集聚过程与经济空间分布不均匀现象的核心思想。知识的溢出效应意味着在区域层面处理创新问题时具有空间依赖性。第二，由于空间创新活动的空间依赖性，容易形成很强的经济活动的空间极化特征，这种非均匀的空间分布特点意味着创新活动存在很强的空间异质性。因此自20世纪90年代后，随着新经济地理学理论的发展，越来越多的学者(Jaffe，1989[70]；Jaffe et al.，1993[71]；Audretsch和Feldman，1996[72])将空间计量经济学用于区域创新活动的经验分析。利用空间计量方法确定知识空间溢出效应方面，代表性的有Anselin et al.(1997)[73]，Autant-Bernard 和 LeSage(2011)[74]，Marrocu和Usai(2013)[75]，Meliciani和Savona(2014)[76]等的研究；在利用空间计量工具解释知识传播机制方面，代表性的有Lee et al.(2010)[77]和Frachisse(2011)[78]的研究。Autant-Bernard(2012)[79]曾对空间计量在创新方面的应用做了系统的文献研究，他认为空间经济学分析方法能更好地量化知识经济，测量其空间分布，探索其潜在机制，尤其是在空间距离和社会距离间的互动方面。动态空间面板模型(Lee和Yu，2010)[80]的最新进展为调查空间知识流向和创新网络开拓了新的研究方向，而这两个问题应该是新经济地理分析研究中最为紧要的问题。

当然，空间计量经济学作为一个工具也正渗透到其他领域。在美国房地产泡沫破裂之后，更简单且更细化的房地产估价方法成为学术界研究热点。Krause和Bitter(2012)[81]对这方面的应用前景做了研究，他认为有三个方面的应用趋势：(1)空间计量经济学在房地产估价方面的拓展研究；(2)土地价值与开发价值差异的研究；(3)对来源于可持续发展模型的价值溢价的研究。此外，Le Gallo和Kamarianakis(2011)[82]分析了1975-2002年欧盟区域生产率的差异演变；Pede et al.(2012)[83]研究了区域收入差距与经济增长问题；Gravelle et al.(2013)[84]用空间计量方法研究了医院服务质量与竞争问题等。

六结语

与以往空间计量经济学的文献综述视角有所不同，本文更关注该学科系统性和应用性，并没有对很多技术性的、理论的问题进行深入讨论。国内研究对空间计量经济学的一些概念理解存在不准确方面，对理论进展跟踪不够，这是本文对空间计量经济学研究进展进行梳理的主要原因。在空间权重矩阵设定与处理方面，本文遵循LeSage(2014b)[40]提出的准则，但模型估计结果对空间权重的选择并不敏感，这是近年来空间计量经济学发展存在的最大问题(LeSage和Pace，2014)[19]，在模型选择时可以直接选取SDM/SDEM模型，或者用LeSage和Pace(2009)[16]提出的贝叶斯后验概率方法，动态模型的估计可选用GMM估计法。受制于应用程序开发的滞后，国内文献对最近发展的理论模型应用存在不足，需要增强跨学科研究。

一方面，对于空间计量经济学的各种批评声音早已有之，最近的代表文献有Pinkse和Slade(2010)[85]，McMillen(2010)[86], Corrado和Fingleton(2012)[87]，Partridge et al.(2012)[88]以及Gibbons和Overman(2012)[89]等的研究。有关观点归结起来主要集中在：(1)空间单元变量间相互作用的途径是多样的，而空间计量经济学模型往往只限于某种最直观途径。如果假定空间中只存在一种稳定的均衡，忽略其他有可能的空间作用方式，那么这假定就显然与实际情况不符。(2)由于不能识别变量间的因果关系，所以应放弃传统空间计量经济学方法，使用非参数估计法，并对模型进行改进，使之具有更坚实的理论与经验基础。(3)空间计量经济学对经济变量的因果关系毫无判断力，所以空间计量毫无意义，仅能用于描述性数据分析，应该用“实验主义范式(Experimentalist Paradigm)”取而代之。(4)在区域空间格局演变过程中，无论是由政府还是企业主导，区域总是以一个主体的形式面对空间竞争，容易形成动态空间关系或多重均衡的空间博弈关系，并不像空间计量模型通常设定的空间稳态均衡。另一方面，这些问题与批评也在不断激励着学者们对空间计量经济学的改进与完善。

[参考文献]

[1] Paelinck, J. H. P..L’EfficacitédesMesuresdePolitiqueéconomiqueRégionale,RapportIntroductive[M]. Faculté des Sciences Economique, Centre de Recherches, Namur, 1967.

[2] Paelinck, J., Nijkamp, P..OperationalTheoryandMethodinRegionalEconomics[M]. Farnborough: Saxon House, 1975.

[3] Hordijk, L.. Problem in Estimating Econometric Relational in Space[J].PapersoftheRegionalScienceAssociation, 1979, 42(1): 99-115.

[4] Paelinck, J. H. P., Klaassen, L. H..SpatialEconometrics[M]. Farnborough: Saxon House, 1979.

[5] Anselin, L.. Spatial Econometrics: Methods and Models[J].StudiesinOperationalRegionalScience, 1988a, 85(411):310-330.

[6] Anselin, L., Hudak, S.. Spatial Econometrics in Practice: A Review of Software Options[J].RegionalScienceandUrbanEconomics, 1992, 22(3): 509-536.

[7] Haining, R. P.. Spatial Data Analysis in the Social and Environmental Sciences[C]. Hurtado MA, Moscatelli GN, Godagnone RE, 1990.

[8] Cressie, N..StatisticsforSpatialData,RevisedEdition[M]. New York: John Wiley, 1991.

[9] Anselin, L., Bera, A. K., Florax, R., et al.. Simple Diagnostic Tests for Spatial Dependence[J].RegionalScienceandUrbanEconomics, 1996, 26(1): 77-104.

[10] LeSage, P.. The Theory and Practice of Spatial Econometrics[Z]. A Manual to Accompany the Spatial Econometrics Toolbox, Available at: www.spatial-econometrics.com, 1999.

[11] Krugman, P.. What’s New about the New Economic Geography?[J].OxfordReviewofEconomicPolicy, 1998, 14(2): 7-17.

[12] Anselin, L.. Spatial Effects in Econometric Practice in Environmental and Resource Economics[J].AmericanJournalofAgriculturalEconomics, 2001, 83(3): 705-710.

[13] Florax, R. J., Folmer, H., Rey, S. J.. Specification Searches in Spatial Econometrics: The Relevance of Hendry’s Methodology[J].RegionalScienceandUrbanEconomics, 2003, 33(5): 557-579.

[14] Anselin, L., Florax, R., Rey, S. J. (Eds.).AdvancesinSpatialEconometrics:Methodology,ToolsandApplications[M]. Springer Science & Business Media, 2004.

[15] Arbia, G..SpatialEconometrics:StatisticalFoundationsandApplicationstoRegionalConvergence[M]. Springer Science & Business Media, 2006.

[16] LeSage, P., Pace, R..IntroductiontoSpatialEconometrics[M]. Florida: CRC Press, Taylor & Francis Group, 2009.

[17] Elhorst, J.. Applied Spatial Econometrics: Raising the Bar[J].SpatialEconomicAnalysis, 2010, 5(1): 9-28.

[18] Corrado, L., Fingleton, B.. Where is the Economics in Spatial Econometrics?[J].JournalofRegionalScience, 2012, 52(2): 210-239.

[19] LeSage, J. P., Pace, R. K.. The Biggest Myth in Spatial Econometrics[J].Econometrics, 2014, 2(4): 217-249.

[20] Anselin, L.. Thirty Years of Spatial Econometrics[J].PapersinRegionalScience, 2010, 89(1): 3-25.

[21] Gibbons, S., Overman, H. G.. Mostly Pointless Spatial Econometrics?[J].JournalofRegionalScience, 2012， 52(2): 172-191.

[22] Partridge, M. D., Boarnet, M., Brakman, S., et al.. Introduction: Whither Spatial Econometrics?[J].JournalofRegionalScience, 2012, 52(2): 167-171.

[23] Griffith, D. A., Paelinck, J. H. P.. Non-standard Spatial Statistics and Spatial Econometrics[J].AdvancesinGeographicInformationScience, 2011, 60(10): i105-i106.

[24] Anselin, L., Rey, S. J.. Spatial Econometrics in an Age of CyberGIScience[J].InternationalJournalofGeographicalInformationScience, 2012, 26(12): 2211-2226.

[25] LeSage, P.. Spatial Econometric Panel Data Model Specification: A Bayesian Approach[J].SpatialStatistics, 2014a, 9: 122-145.

[26] Elhorst, J..SpatialPanelDataModelsInSpatialEconometrics[M]. Springer Berlin Heidelberg, 2014a.

[27] Elhorst, J..SpatialEconometrics:FromCross-sectionalDatatoSpatialPanels[M]. Berlin, New York, Dordrecht, London: Springer, 2014b.

[28] Isard, W..LocationandSpace-economy[M]. Massachusetts: The MIT Press, 1956.

[29] Anselin, L.. Spatial Dependence and Spatial Structural Instability in Applied Regression Analysis[J].JournalofRegionalScience, 2006, 30(2): 185-207.

[30] Isard, W..IntroductiontoRegionalScience[M]. New Jersey: Prentice Hall, 1975.

[31] Matheron, G.. Principles of Geostatistics[J].EconomicGeology, 1963, 58(8): 1246-1266.

[32] Moran, P. A. P.. The Interpretation of Statistical Maps[J].JournaloftheRoyalStatisticalSociety, 1947, 10(2): 243-251.

[33] Geary, R. C.. The Contiguity Ratio and Statistical Mapping[J].IncorporatedStatistician, 1954, 5(3): 115-145.

[34] Cliff, A. D., Ord, J. K.. Spatial Autocorrelation[J].EncyclopediaofDatabaseSystems, 1973.

[35] Cliff, A., Ord, K.. Testing for Spatial Autocorrelation Among Regression Residuals[J].GeographicalAnalysis, 1972, 4(3): 267-284.

[36] Anselin, L.. Estimation Methods for Spatial Autoregressive Structures[Z]. Ithaca, N.Y.: Regional Science Dissertation and Monograph Series, 1980.

[37] 林光平, 龙志和, 吴梅. 我国地区经济收敛的空间计量实证分析: 1978-2002年[J]. 经济学(季刊), 2005, S1: 67-82.

[38] Beck, N., Gleditsch, K. S., Beardsley, K.. Space is More than Geography: Using Spatial Econometrics in the Study of Political Economy[J].InternationalStudiesQuarterly, 2006, 50(1): 27-44.

[39] Watts, D. J., Strogatz, S. H.. Collective Dynamics of ‘Small-world’ networks[J].Nature, 1998, 393(6684): 440-442.

[40] LeSage, J. P.. What Regional Scientists Need to Know about Spatial Econometrics[J].AvailableatSSRN2420725, 2014b.

[41] Hordijk, L.. Spatial Correlation in the Disturbances of a Linear Interregional Model[J].RegionalandUrbanEconomics, 1974, 4(2): 117-140.

[42] Burridge, P.. On the Cliff-ord Test for Spatial Autocorrelation[J].JournaloftheRoyalStatisticalSociety， 1980, 42: 107-108.

[43] Kelejian, H., Robinson, D.. Spatial Autocorrelation: A New Computationally Simple Test with an Application to Per Capita Country Policy Expenditures[J].RegionalScienceandUrbanEconomics, 1992, 22(3): 317-331.

[44] Bera, A. K., Yoon, M. J.. Simple Diagnostic Tests for Spatial Dependence[J].Champaign:UniversityofIllinoisatUrbana-Champaign, 1992, 26(95): 77-104.

[45] Anselin, L.. Testing for Spatial Dependence in Linear Regression Models: A Review[Z]. Morgantown: West Virginia University, Regional Research Institute Research Paper, 1994: 94-16.

[46] Anselin, L.. Lagrange Multiplier Test Diagnostics for Spatial Dependence and Spatial Heterogeneity[J].GeographicalAnalysis, 1988b, 20(1):1-17.

[47] 张志强. 空间加权矩阵设置与空间面板参数估计效率[J]. 数量经济技术经济研究, 2014, (10): 122-138.

[48] Anselin, L., Florax, R.. New Directions in Spatial Econometrics: Introduction[J].AdvancesinSpatialScience, 1995: 3-18.

[49] 孙洋. 空间计量模型中空间矩阵的误用及其影响[J]. 统计研究, 2009, 26(6): 85-91.

[50] 陈青青, 龙志和, 林光平. 空间滞后模型的空间相关性稳健检验[J]. 管理工程学报, 2014, 28(2): 73-78, 72.

[51] Zellner, A..AnIntroductiontoBayesianInferenceinEconometrics[M]. New York: John Wiley & Sons, 1971.

[52] Madigan, D., York, J.. Bayesian Graphical Models for Discrete Data[J].InternationalStatisticalReview, 1995, 63(2): 215-232.

[53] Ord, K.. Estimation Methods for Models of Spatial Interaction[J].JournaloftheAmericanStatisticalAssociation, 1975, 70(349): 120-126.

[54] Lee, L. F.. Asymptotic Distribution of Quasi-maximum Likelihood Estimators for Spatial Autoregressive Models[J].Econometrica, 2004, 72(6): 1899-1925.

[55] Kelejian, H., Prucha, R.. A Generalized Spatial Two Stage Least Squares Procedure for Estimating a Spatial Autoregressive Model with Autoregressive Disturbances[J].JournalofRealEstateFinance&Economics, 1998, 17(1): 99-121.

[56] LeSage, P.. Bayesian Estimation of Spatial Autoregressive Models[J].InternationalRegionalScienceReview, 1997, 20(20): 113-129.

[57] Liu, X., Lee, L. F.. Two-stage Least Squares Estimation of Spatial Autoregressive Models with Endogenous Repressors and Many Instruments[J].EconometricReviews, 2013, 32(5-6): 734-753.

[58] Yu, J., Jong, R., Lee, L.. Quasi-maximum Likelihood Estimators for Spatial Dynamic Panel Data with Fixed Effects When both N and T are large[J].JournalofEconometrics, 2008, 146(1): 118-134.

[59] Lee, L. F., Yu, L.. Efficient GMM Estimation of Spatial Dynamic Panel Data Models with Fixed Effects[J].JournalofEconometrics, 2014, 180(2): 174-197.

[60] Parent, O., LeSage, P.. A Spatial Dynamic Panel Model with Random Effects Applied to Commuting Times[J].TransportationResearchPartBMethodological, 2010, 44(5): 633-645.

[61] Parent, O., LeSage, P.. A Space-time Filter for Panel Data Models Containing Random Effects[J].ComputStatData, 2011, 55(1): 475-490.

[62] Franzese, J., Hays, C.. Spatial Econometric Models of Cross-sectional Interdependence in Political Science Panel and Time-series-cross-section Data[J].PolitAnal, 2007, 15(2): 140-164.

[63] Kukenova, M., Monteiro, A.. Spatial Dynamic Panel Model and System GMM: A Monte Carlo Investigation[Z]. http://ideas.repec.org/p/pra/mprapa/11569.html, 2009.

[64] Baltagi, B. H., Fingleton, B., Pirotte, A.. Estimating and Forecasting with a Dynamic Spatial Panel Data Model[J].OxfordBulletinofEconomicsandStatistics, 2014, 76(1): 112-138.

[65] Sen, A., Smith, T. E..GravityModelsofSpatialInteractionBehavior[M]. Heidelberg: Springer-Verlag, 1995.

[66] LeSage, P., Pace, R.. Spatial Econometric Modeling of Origin Destination Flows[J].JournalofRegionalScience, 2008, 48(5): 941-967.

[67] LeSage, J. P., Polasek, W.. Incorporating Transportation Network Structure in Spatial Econometric Models of Commodity Flows[J].SpatialEconomicAnalysis, 2008, 3(2): 225-245.

[68] Holloway, G., Shankara, B., Rahman, S.. Bayesian Spatial Probit Estimation: A Primer and an Application to HYV Rice Adoption[J].AgriculturalEconomics, 2002, 27(3): 383-402.

[69] Marshall, A..PrincipesD′ÉconomiePolitique[M]. Paris, London & New York, Gordon & Breach,1920, reprint 1971, Vol.2: 576.

[70] Jaffe, A.. Real Effects of Academic Research[J].TheAmericanEconomicReview, 1989, 79(5): 957-970.

[71] Jaffe, A., Trajtenberg, M., Henderson, R.. Geographic Localization of Knowledge Spillovers as Evidenced by Patent Citations[J].TheQuarterlyJournalofEconomics, 1993, 108(3): 577-598.

[72] Audretsch, D., Feldman, M.. R&D Spillovers and the Geography of Innovation and Production[J].TheAmericanEconomicReview, 1996, 86(3): 630-640.

[73] Anselin, L., Varga, A., Acs, Z.. Local Geographic Spillovers between University Research and High Technology Innovations[J].JournalofUrbanEconomics, 1997, 42(3): 422-448.

[74] Autant-Bernard, C., LeSage, J.. Quantifying Knowledge Spillovers Using Spatial Econometric Tools[J].JournalofRegionalScience, 2011, 51(3): 471-496.

[75] Marrocu, E., Paci, R., Usai, S.. Proximity, Networking and Knowledge Production in Europe: What Lessons for Innovation Policy?[J].TechnologicalForecastingandSocialChange, 2013, 80(8): 1484-1498.

[76] Meliciani, V., Savona, M.. The Determinants of Regional Specialisation in Business Services: Agglomeration Economies, Vertical Linkages and Innovation[J].JournalofEconomicGeography, 2014, 15(2): 387-416.

[77] Lee, L-F., Liu, X., Lin, X.. Specification and Estimation of Social Interaction Models with Network Structures[J].EconometricsJournal, 2010, 13(2): 145-176.

[78] Frachisse, D.. Structures et de′terminants des collaborations au sein des programmes cadres de recherche et de′veloppement technologique de l’Union Europe′enne[D]. Une perspective re′seau, PhD Thesis, 2011.

[79] Autant-Bernard, C.. Spatial Econometrics of Innovation: Recent Contributions and Research Perspectives[J].SpatialEconomicAnalysis, 2012, 7(4): 403-419.

[80] Lee, L-F., Yu, J.. Some Recent Developments in Spatial Panel Data Models[J].RegionalScienceandUrbanEconomics, 2010, 40(5): 255-271.

[81] Krause, A. L., Bitter, C.. Spatial Econometrics, Land Values and Sustainability: Trends in Real Estate Valuation Research[J].Cities, 2012, 29: 19-S25.

[82] Le Gallo, J., Kamarianakis, Y.. The Evolution of Regional Productivity Disparities in the European Union from 1975 to 2002: A Combination of Shift-share and Spatial Econometrics[J].RegionalStudies, 2011, 45(1): 123-139.

[83] Pede, V. O., Sparks, A. H., McKinley, J. D.. Regional Income Inequality and Economic Growth: A Spatial Econometrics Analysis for Provinces in the Philippines[R]. Manila: International Rice Research Institute, 2012.

[84] Gravelle, H., Santos, R., Siciliani, L.. Does a Hospitals Quality Depend on the Quality of Other Hospitals? A Spatial Econometrics Approach to Investigating Hospital Quality Competition[J].WorkingPapers, 2013: 203-216.

[85] Pinkse, J., Slade, M. E.. The Future of Spatial Econometrics[J].JournalofRegionalScience, 2010, 50(1): 103-117.

[86] McMillen, D. P.. Issues in Spatial Data Analysis[J].JournalofRegionalScience, 2010, 50(1): 119-141.

[87] Corrado, L., Fingleton, B.. Where is the Economics in Spatial Econometrics?[J].JournalofRegionalScience, 2012, 52(2): 210-239.

[88] Partridge, M. D., Boarnet, M., Brakman, S., et al.. Introduction: Whither Spatial Econometrics?[J].JournalofRegionalScience, 2012, 52(2): 167-171.

[89] Gibbons, S., Overman, H. G.. Mostly Pointless Spatial Econometrics?[J].JournalofRegionalScience, 2012, 52(2): 172-191.

[责任编辑：陈林]

[DOI]10.14007/j.cnki.cjpl.2016.01.001

[引用方式]张可云, 杨孟禹. 国外空间计量经济学研究回顾、进展与述评[J]. 产经评论, 2016, 7(1): 5-21.

Review and Comment on the Research of Spatial Econometrics

ZHANG Ke-yunYANG Meng-yu

Abstract:Based on the inherent essence and the basic principle, the two basic concepts and three key problems and applications of Spatial Econometrics, combining with the spatial econometrics theory context, the paper focused on the basic concept of spatial econometrics, and the spatial effect test, weight setting, model estimation problem in the modeling process of spatial econometrics. Combined with the latest research progress, the paper summarized the problems that should be paid attention in the application of spatial econometric models, and analyzed the existed problems in the propagation process of the spatial econometrics, such as unclear concept, confusion and misleading misinformation. At last, the paper pointed out the problems and development directions of spatial econometrics.

Key words:spatial econometrics; spatial effect; spatial econometric model; revelation of regional economic research

[中图分类号]F224.0

[文献标识码]A

[文章编号]1674-8298(2016)01-0005-17

[作者简介]张可云，中国人民大学经济学院教授、博士生导师，主要研究方向为区域关系与区域政策；杨孟禹，中国人民大学经济学院博士研究生，主要研究方向为区域关系和区域政策。

[基金项目]中央在京高校重大成果转化项目“京津冀协同一体化发展研究”(总项目主持人：刘元春，子项目主持人：张可云)；中国人民大学2015年度拔尖创新人才培育资助计划。

[收稿日期]2015-10-22