一类新无限维李子代数的同构和同态

余德民

(湖南理工学院数学学院,湖南岳阳　414000)



一类新无限维李子代数的同构和同态

余德民

(湖南理工学院数学学院,湖南岳阳414000)

摘要：构造了一类由三个基本元生成的无限维李代数.证明了这类无限维李代数是Virasoro-like李代数的推广.此外,研究了这类李子代数同构和同态.

关键词：李代数;同构;同态

1　引言

Virasoro-like李代数是在上世纪八十年代作为拟多项式环的一阶微分算子代数被引入的, 90年代在理论物理的广义对称性研究中产生了同样的代数结构.设C为复数域, Z为整数加群,文献[1]定义了一类Virasoro-like李代数,并研究了Virasoro-like李代数的单性,设是由L(a1,a2)(∀a1,a2∈Z),生成的复数域C上的线性空间,李运算定义如下:

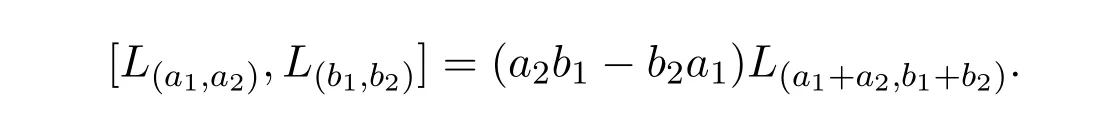
此运算在基向量上线性扩张,并满足反对称性和Jacobi不等式,称为Virasoro-like李代数.文献[2]研究了Virasoro-like李代数的导子代数和导子代数的自同构群,文献[3]研究了带参数的α,β的Virasoro-like的导子代数,文献[4]研究了广义Virasoro李代数.文献[5-9]研究了Virasoro李代数及其推广的Virasoro李代数.本文推广了Virasoro-like李代数和Virasoro-like李代数,构造了李代数g,并发现李代数g是一类特殊的李代数,有一些良好的性质. g为C上线性空间,其基向量为:

在g上定义李运算为:∀k1,k2,k3,q1,q2,q3∈Z,

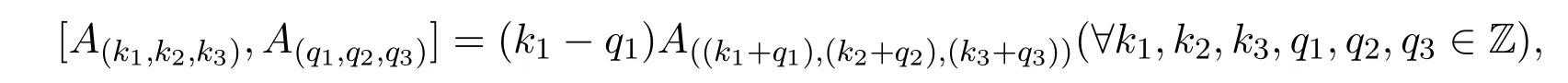
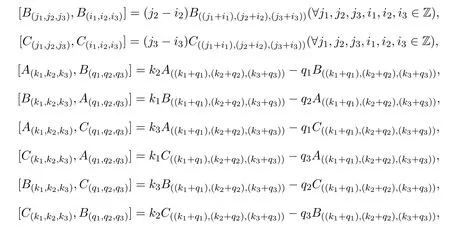
其中∀k1,k2,k3,q1,q2,q3∈Z.

然后在基上双线性扩张.可验证运算满足反对称性和Jacobi恒等式,从而g为无限维李代数.设由A(k1,k2,k3)生成的子代数为g1(∀k1,k2,k3∈Z),由B(k1,k2,k3)生成的子代数为g2(∀k1,k2,k3∈Z),由C(k1,k2,k3)生成的子代数为g3(∀k1,k2,k3∈Z),由A(k1,k2,k3),B(q1,q2,q3)生成的子代数为g4(∀k1,k2,k3,q1,q2,q3∈Z),由A(k1,k2,k3),C(q1,q2,q3)生成的子代数为g5(∀k1,k2,k3,q1,q2,q3∈Z),由B(k1,k2,k3),C(q1,q2,q3)生成的子代数为g6(∀k1,k2,k3,q1,q2,q3∈Z).

本文主要研究了李代数g的的李子代数g1,g2,g3,g4,g5,g6间的同构,同态.

2　主要结果

构造g1到g2映射如下:

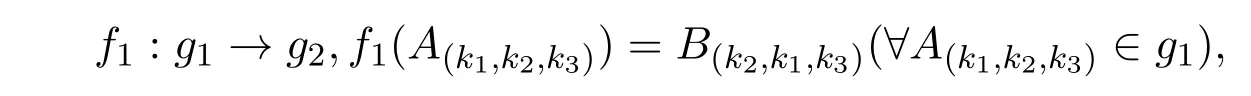
f1在g1的基向量A(k1,k2,k3)上线性扩张.

定理2.1 f1是g1到g2同构.

证明从构造知f1是g1到g2同构的线性映射,且既是单射又是满射.可验证

从而

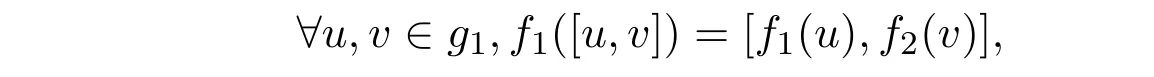
从而f1是g1到g2同构.

构造g1到g3映射如下:

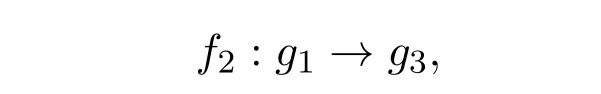
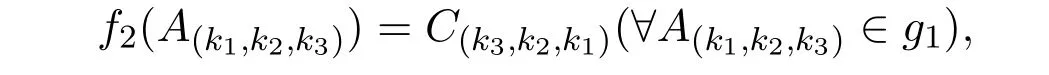
f2在g1的基向量A(k1,k2,k3)上线性扩张.

定理2.2 f2是g1到g3同构.

证明从构造知f2是g1到g3同构的线性映射,且既是单射又是满射.可验证

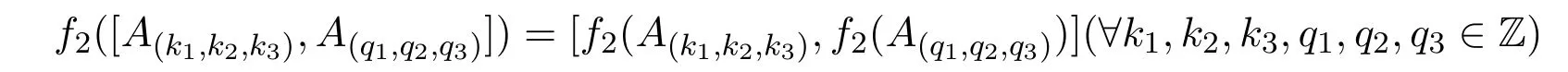
从而

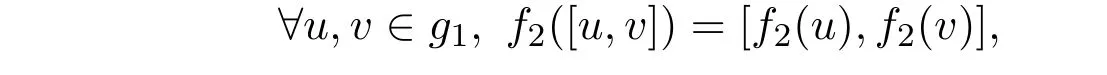
从而f2是g1到g3同构.

构造g2到g3映射如下:

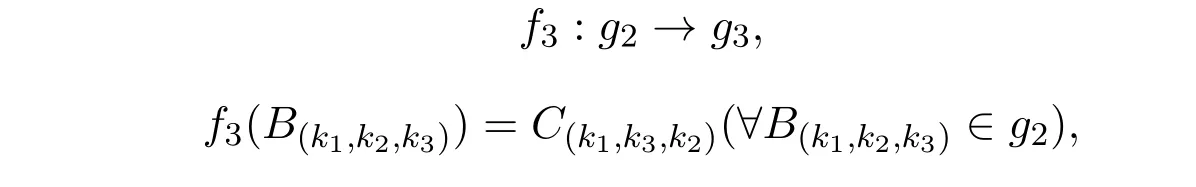
f3在g1的基向量B(k1,k2,k3)上线性扩张.

定理2.3 f3是g2到g3同构.

证明从构造知f3是g1到g3同构的线性映射,且既是单射又是满射.可验证

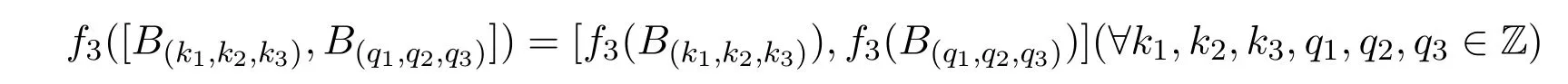
从而

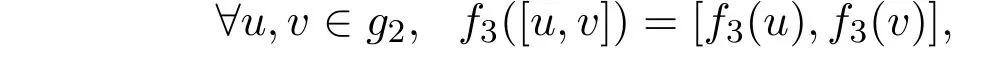
从而f3是g2到g3同构.

构造g1上的自同态映射如下:

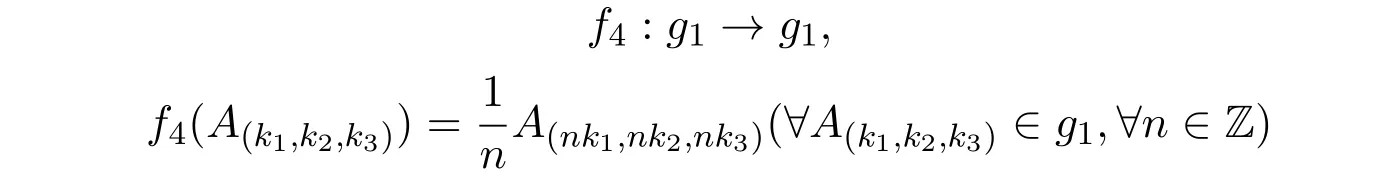
f4在g1的基向量A(k1,k2,k3)上线性扩张.

定理2.4 f4是g1的单自同态.

证明从构造知f4为g1上的线性映射,且是单射.

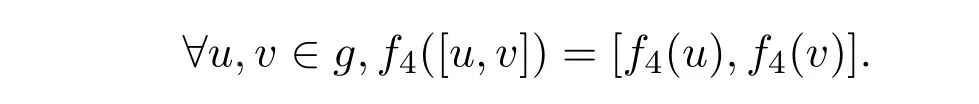
在定理2.4中,单自同态f4有如下特殊情形.当n = 1时, f4为恒等同构.当n1=−1 时,f4为同构.构造g2上的自同态映射如下:

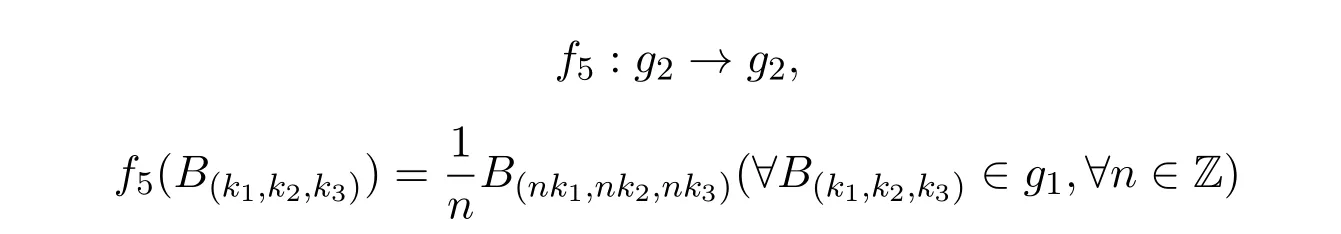
f5在g1的基向量B(k1,k2,k3)上线性扩张.

定理2.5 f5是g2的单自同态.

证明从构造知f5为g2上的线性映射,且是单射.

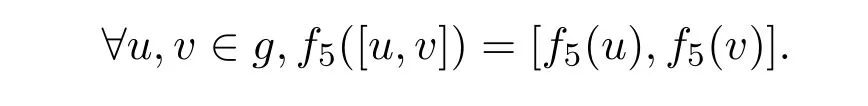
在定理2.5中,单自同态f5有如下特殊情形.

当n = 1时, f5为恒等同构.当n1=−1时, f5为同构.构造g3上的自同态映射如下:

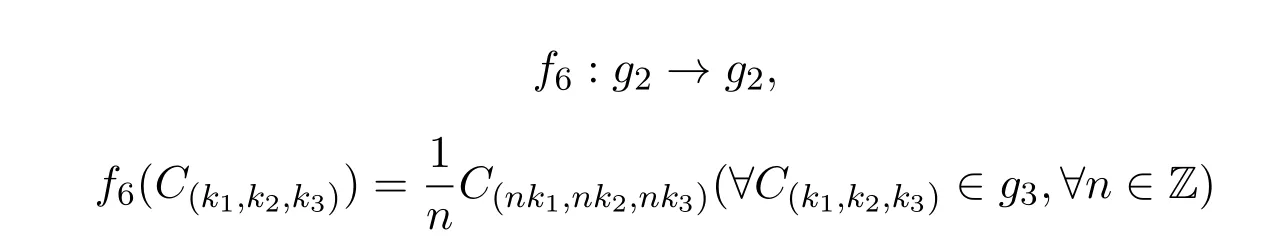
f5在g1的基向量C(k1,k2,k3)上线性扩张.

定理2.6 f6是g3的单自同态.

证明从构造知f6为g3上的线性映射,且是单射.

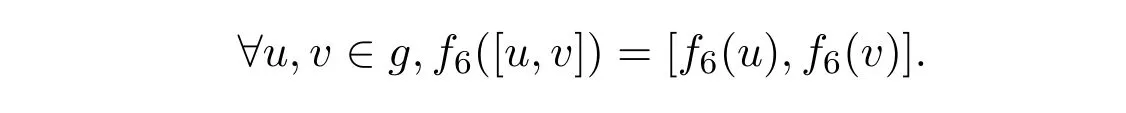
在定理2.6中,单自同态f6有如下特殊情形.

当n = 1时,f6为恒等同构.当n1=−1时,f6为同构.

构造g4到g4映射如下:

定理2.7 f7是g4的自同构.

证明从构造知f7是g4到g4同构的线性映射,且既是单射又是满射.可验证

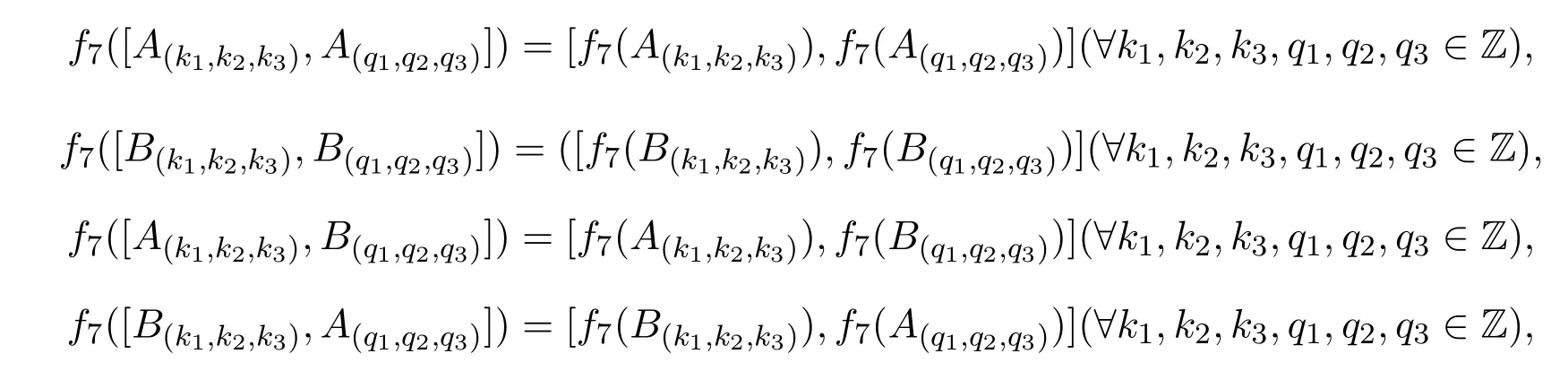
从而

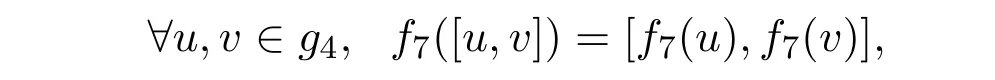
从而f7是g4到g4同构.

构造g5到g5映射如下:

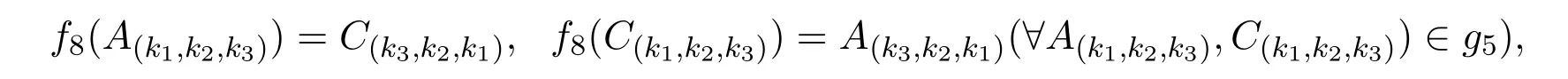
f8在g5的基向量A(k1,k2,k3),C(k1,k2,k3)上线性扩张.

定理2.8 f8是g5的自同构.

证明从构造知f8是g5到g5同构的线性映射,且既是单射又是满射.可验证

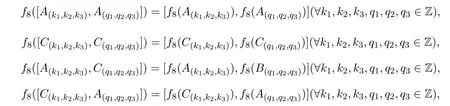
从而

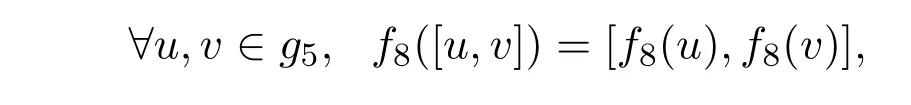
故f8是g5到g5同构.

参考文献

[1] Zhang H, Zhao K. Represent of Virasoro Lie algebra and its q-analog [J]. Comm. Alg., 1996,24(14):4361-4372.

[2]姜翠波,孟道骥. Virasoro-相似代数的导子代数[J].数学进展, 1998,27(2):175-184.

[3]徐海霞,卢才辉.无限维李代数L(α,β)的导子代数[J].数学学报(中文版), 1998,41(4):859-864.

[4] Su Y, Zhao K. Generalized Virasoro and Super-Virasoro Algebras and modules of the intermediate series [J]. J. Algebra, 2002,252:1-19.

[5]余德民,卢才辉. Virasoro李代数的子代数若干结果[J].数学学报(中文版), 2006,49(3):633-638.

[6]余德民,梅超群.一类无限维半单李代数[J].系统科学与数学(中文版), 2008,28(9):1101-1108.

[7]余德民,卢才辉.李代数L(Z,f,δ)的特殊性质[J].数学进展, 2006,35(6):707-711.

[8]余德民,卢才辉. Virasoro李代数的子代数的同构及生成元[J].系统科学与数学(中文版), 2008,28(1):24-29.

[9]余德民,梅超群,郭晋云.一些特殊项链李代数的同态[J].数学年刊(中文版), 2009,30(4):551-562.

2010 MSC: 17B05, 17B30

Isomorphisms and homomorphisms of a new infinite dimensional Lie algebra

Yu Deming
(Department of Mathematics, Hu′nan Institute of Science and Technology, Yueyang 414000, China)

Abstract:A new infinite dimensional Lie algebra generating by three basic element is a generalization of Virasoro-like Lie algebra. Also, isomorphisms and homomorphisms of this class of algebra are studied.

Key words:Lie algebra, isomorphisms, homomorphisms

作者简介：余德民(1975-),博士,副教授,研究方向:李代数、代数表示论.

基金项目：湖南省教育厅一般项目(14C0523);湖南省重点建设学科建设项目.

收稿日期：2015-09-10.

DOI：10.3969/j.issn.1008-5513.2016.01.003

中图分类号：O152.5

文献标识码：A

文章编号：1008-5513(2016)01-0014-05