多目标优化问题拟近似有效解非线性标量化的一个注记

李小燕,高英

(重庆师范大学数学科学学院,重庆400047)



多目标优化问题拟近似有效解非线性标量化的一个注记

李小燕,高英

(重庆师范大学数学科学学院,重庆400047)

摘要：主要研究多目标优化问题拟近似(弱)有效解.在没有任何凸性假设下,通过非线性标量化方法给出了多目标优化问题拟近似(弱)有效解的充分条件.主要结果修正了已有文献中的错误,并通过例子对其错误进行了说明.

关键词：多目标优化;拟近似有效解;非线性标量化

1　引言

在多目标优化问题中,解的定义,最优性条件和对偶理论是十分重要的课题,对其理论研究也越来越多[1-21].其中,如何定义解的概念是首要的问题.近几十年来,多目标优化问题近似解的概念陆续被许多学者提出.文献[10-11]首先引进了ε-有效解的概念.文献[12]研究了六种不同类型的ε-有效解.后来,又有一些学者提出几种其他类型的ε-有效解[13-14].受文献[14]研究工作的启发,文献[15-16]又提出了近似Benson真有效解的概念.有了这些解的概念之后,对它们的理论研究也随之丰富起来[15-20].本文主要针对文献[20]中的拟近似(弱)有效解,在没有任何凸性条件下研究其非线性标量化刻画,修正文献[20]中主要结果的错误.

令Rn为n维欧氏空间, Rn+为其非负象限.本文将用到如下的偏序关系:x≤y的否定记为x /≤y.

文献[20]考虑如下的多目标优化问题:

其中, X⊂Rn非空, fi: X→R, i = 1,···,m.记M = {1,···,m}.

(i)称x0为(MOP)的拟有效解,若

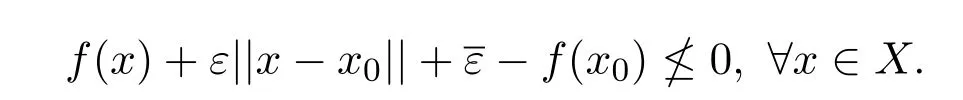
(ii)称x0为(MOP)的拟弱有效解,若

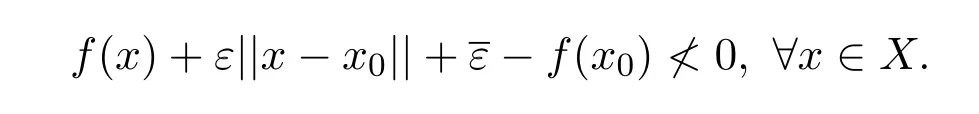
文献[20]针对定义1.1的两种近似解,利用一种非线性标量化函数给出了其最优性充要条件.但充分性的证明存在错误.本文将通过例子说明其充分性不一定成立,并对该错误进行修正,建立正确的充分条件.

2　主要结果

文献[20]利用文献[21]中的定理,研究了(MOP)的拟弱有效解非线性标量化,得到了如下结果.

定理2.1[20]设x0∈X,则x0为(MOP)的拟弱有效解当且仅当对任意的y∗i＜ fi(x0), i∈M, x0是如下标量化问题的拟最优解

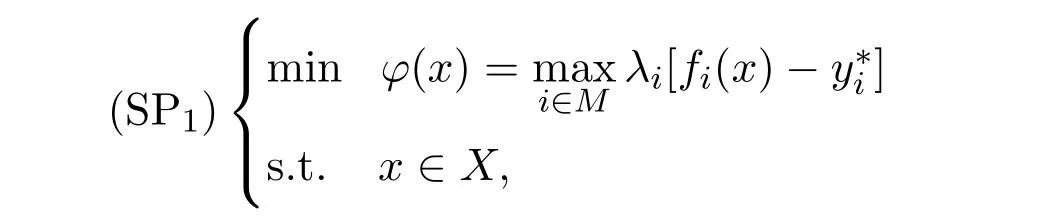
注意到文献[20]中,对定理2.1充分性的证明用到了如下的结果:对任意的

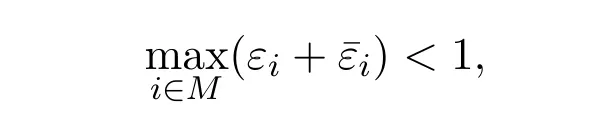
则有

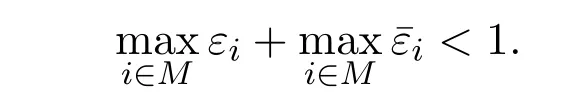
事实上,以上结论不一定成立,见如下例子.

而

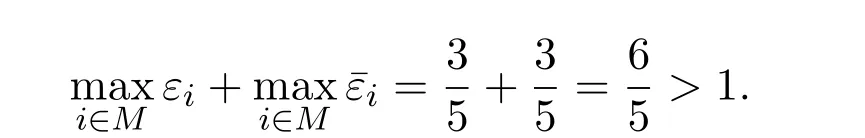
这一错误导致定理2.1的充分性结果不一定成立,参见如下的例子.

例2.2在(MOP)中,令

则定理2.1的充分条件是成立的,即对任意的y∗i＜fi(x0) = 0,i = 1,2, x0是(SP1)的一个拟最优解.但x0= 0不是(MOP)问题的拟弱有效解.

事实上,

也就是x0= 0不是(MOP)的拟弱有效解.

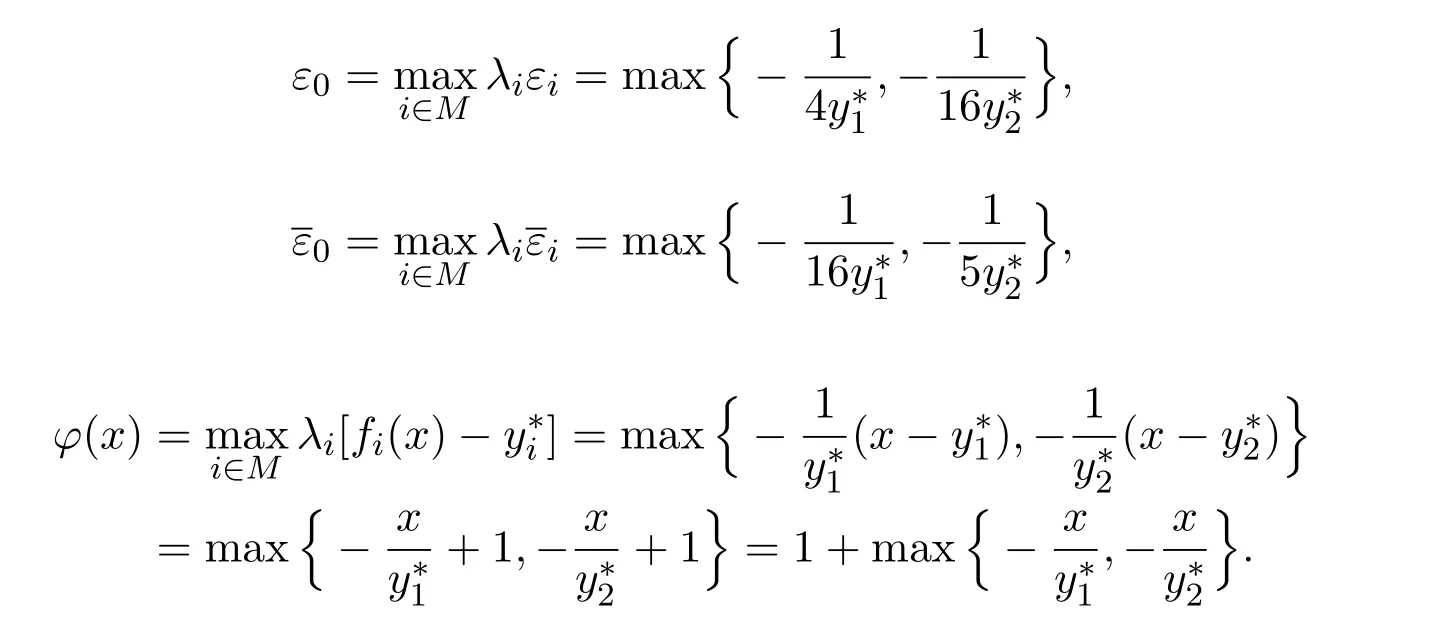
需证

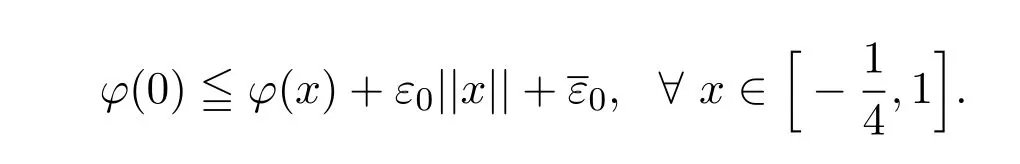
上式等价于

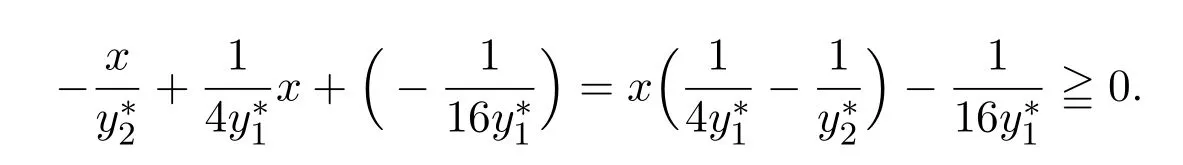
即

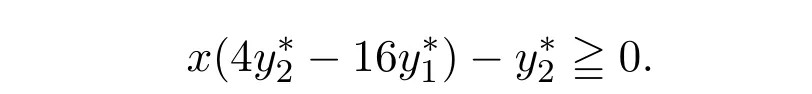
即

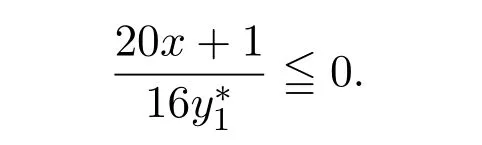
即

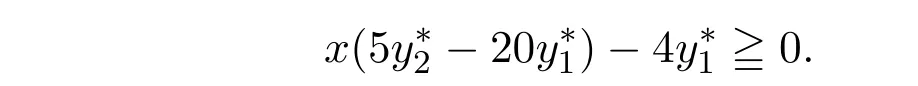
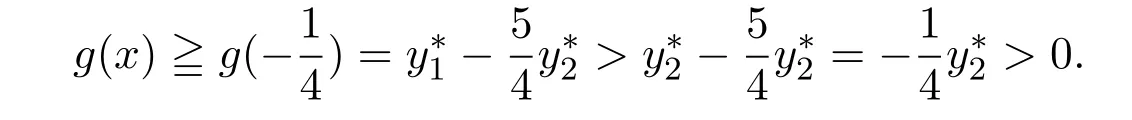
即

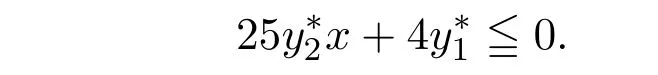
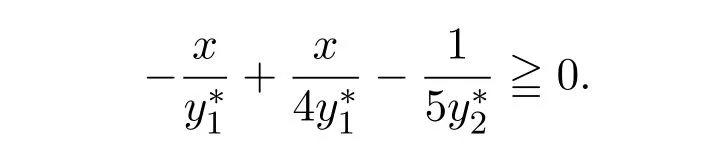
即

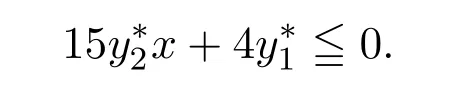
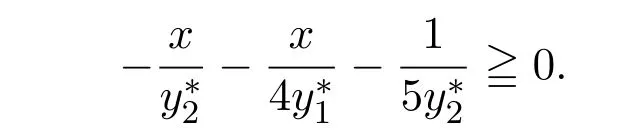
即

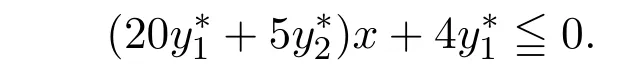
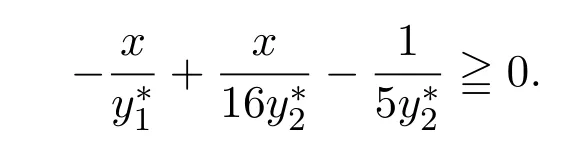
即

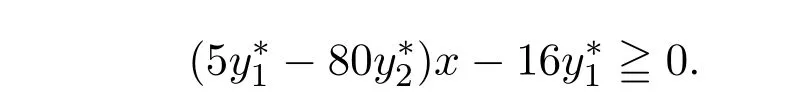
令

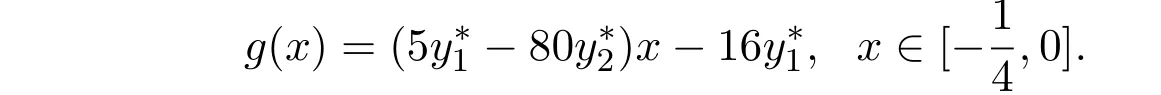
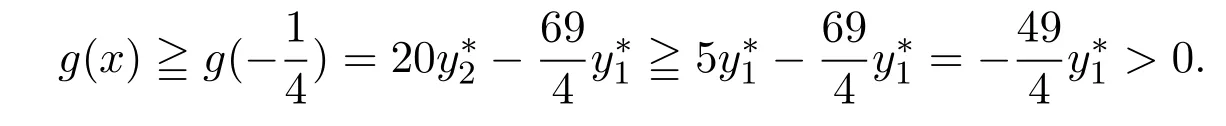
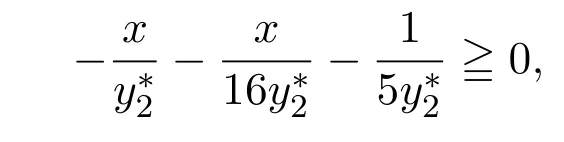
即

下面,给出正确的充分性结果.

因此,若

则有

利用上面的结果给出如下正确的充分条件.

定理2.2设x0∈X,若对任意的是如下的标量化问题的拟最优解

则x0是(MOP)的一个拟弱有效解.其中

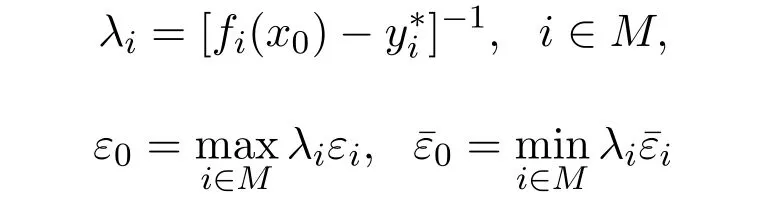
或

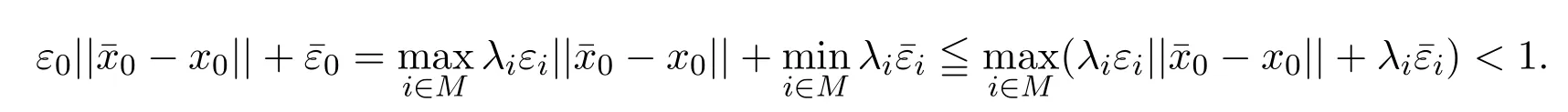
或

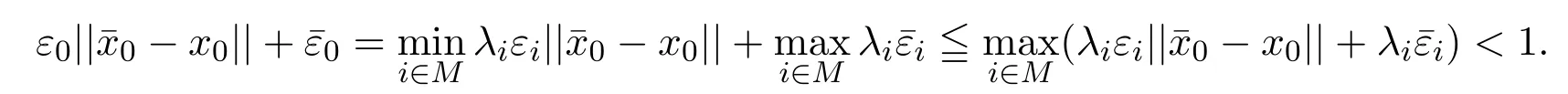
类似文献[20]定理2.1的证明,可得0＞0的矛盾.因此x0= 0是(MOP)的一个(ε,¯ε)-拟弱有效解.

注2.2定理2.1的必要性是成立的.但定理2.2的必要性不一定成立.参见如下的例子.

例2.3在(MOP)中,令

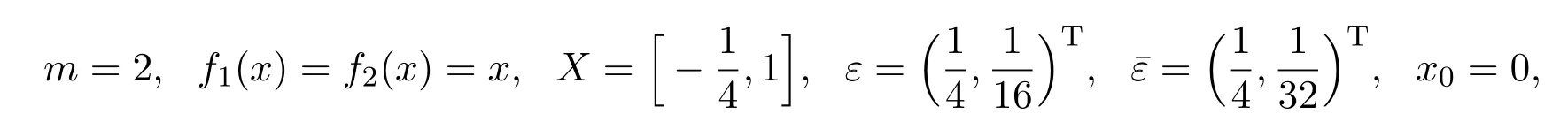
容易证明x0= 0是(MOP)的(ε,¯ε)-拟弱有效解.令

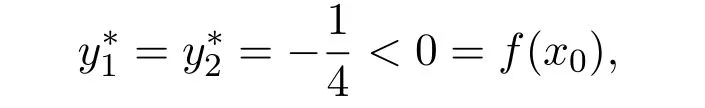
则

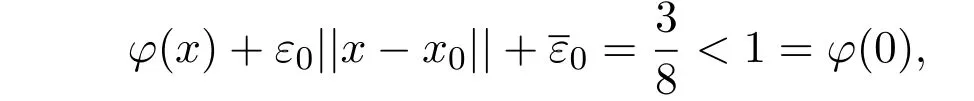
可以发现文献[20]中定理4和定理5的证明过程中也出现了类似的错误.首先给出文献[20]中的定理4和定理5,见定理2.3和定理2.4.

定理2.3[20]设x0∈X,若对任意的i∈M, x0是如下标量化问题的拟最优解

则x0是(MOP)的拟有效解.其中

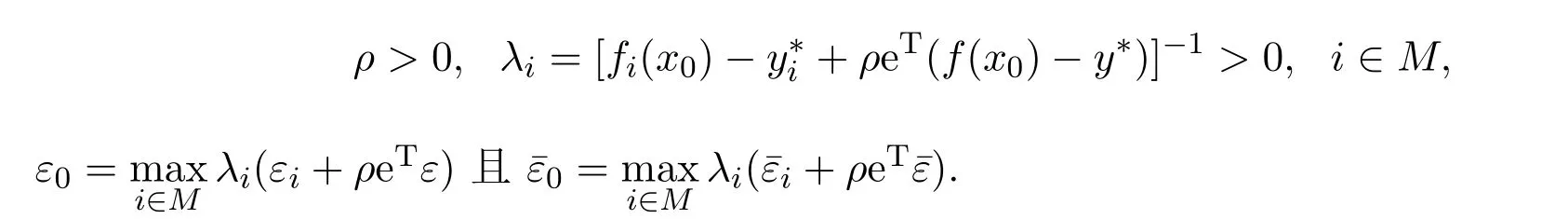
定理2.4[20]设x0∈X,若对任意的i∈M, x0是如下标量化问题的拟最优解

则x0是(MOP)的拟有效解.其中

在文献[20]中对定理2.3的证明用到了如下结果:由

有

根据前面的讨论上式是不一定成立的.因此,定理2.3不一定成立.类似地可以给出修正的充分条件(见定理2.5).事实上,由(2.2)式可以得到:

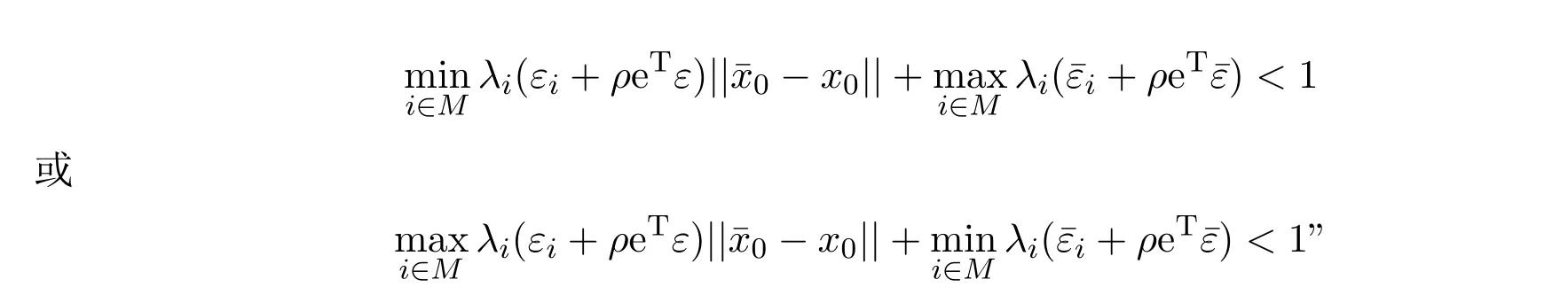
同样地,文献[20]中对定理2.4的证明也出现了类似的错误,作者用到了如下的结果:由

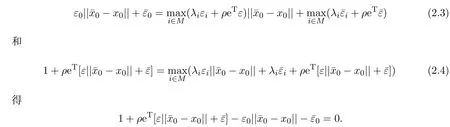
显然,上式不一定成立.因此,文献[20]定理5不一定成立.此外,由(2.3)式和(2.4)式可得:

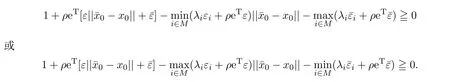
由此,可以给出修正的充分条件(见定理2.6).

定理2.5设x0∈X,若对任意的i∈M, x0是如下标量化问题的拟最优解

则x0是(MOP)的拟有效解.其中

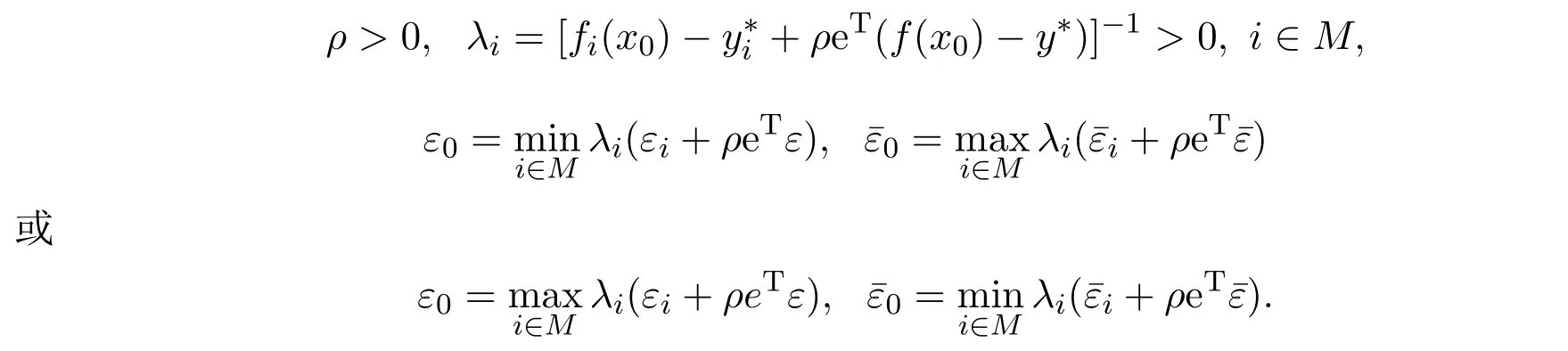
定理2.6设x0∈X,若对任意的i∈M, x0是如下标量化问题的拟最优解

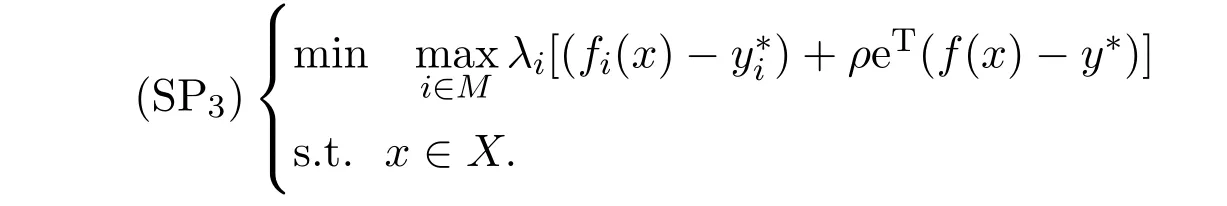
则x0是(MOP)的拟有效解.其中

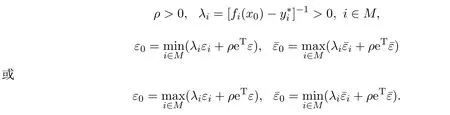
参考文献

[1] Geoffrion A M. Proper efficiency and the theory of vector maximization [J]. Journal of Mathematical Analysis and Applications, 1968,22:618-630.

[2]高英.一类多目标广义分式规划问题的最优性条件和对偶[J].纯粹数学与应用数学, 2011,27(4):477-485.

[3] Li Z F, Wang S Y. Lagrange multipliers and saddle points in multiobjective programming [J]. Journal of optimization theory and applications, 1994,83:63-81.

[4] Li Z F, Chen G Y. Lagrangian Multipliers, saddle points and duality in vector optimization of Set-Valued maps [J]. Journal of Mathematical Analysis and Applications, 1997,215:297-316.

[5] Li Z. A theorem of the alternative and Its application to the optimization of Set-Valued maps [J]. Journal of Optimization Theory and Applications, 1999,100(2):365-375.

[6]高英.非可微多目标优化问题的高阶逆对偶定理[J].纯粹数学与应用数学, 2014, 30(2):136-142.

[7] Yang X M, Yang X Q, Teo K L. Converse duality in nonlinear programming with cone constraints [J]. European Journal of Operational Reasearch, 2006,170:350-354.

[8] Mishra S K, Wang S Y, Lai K K. Higher-order duality for a class of nondifferentiable multiobjective programming problems involving generalized type I and related function [J]. J. Syst. Sci. Complex., 2011,24:883-891.

[9]李红梅,高英.一类锥约束多目标优化问题的高阶对偶研究[J].纯粹数学与应用数学, 2015,31(1):73-84.

[10] Kutateladze S S. Convex-programming [J]. Sov. Math. Dokl., 1979,20:390-393.

[11] Loridan P.ε-solutions in vector minimization problems [J]. Journal of Optimization Theory and Applications, 1984,43(2):265-276.

[12] White D J. Epsilon efficiency [J]. Journal of Optimization Theory and Applications, 1986,49(2):319-337.

[13] Helbig S, Pateva D. On several concepts for ε-efficiency [J]. OR Spektrum, 1994,16(3):179-186.

[14] Guti´errez C, Jim´enez B, Novo V. A unified approach and optimality conditions for approximate solutions of vector optimization problems [J]. SIAM Journal on Optimization, 2006,17:688-710.

[15] Gao Y, Yang X M, Teo K L. Optimality conditions for approximate solutions of vector optimization problems [J]. Journal of Industrial and Management Optimization, 2011,7:483-496.

[16] Gao Y, Hou S H, Yang X M. Existence and optimality conditions for approximate solutions to vector optimization problems [J]. Journal of Optimization Theory and application, 2012,152:97-120.

[17] Engau A, Wiecek M M. Generating ε-efficient solutions in multiobjective programming [J]. European Journal of Operational Research, 2007,177:1566-1579.

[18] Ghaznavi B A, Khorram E. On approximating weakly/properly efficient solutions in multi-objective programming [J]. Mathematical and Computer Modelling, 2011,54:3172-3181.

[19] Ghaznavi B A, Khorram E, Soleimani-Damaneh M. Scalarization for characterization of approximate strong/weak/proper efficiency in multiobjective optimization [J]. Optimization, 2013,62(6):703-720.

[20] Beldiman M, Panaitescu E, Dogaru L. Approximate quasi efficient solutions in multiobjective optimization [J]. Bull. Math. Soc. Math. Roumanie Tome, 2008,51(2):109-121.

[21] Kaliszewski I. A theorem on nonconvex functions and its application to vector optimization [J]. European Journal of Operational Research, 1995,80:439-449.

2000 MSC: 90C32, 90C46, 90C47

A note on nonlinear scalarizations of approximate quasi efficient solutions

Li Xiaoyan , Gao Ying
(Department of Mathematics, Chongqing Normal University, Chongqing 400047, China)

Abstract:In this paper, we consider approximate quasi (weakly) efficient solutions of multiobjective programming problems and give some sufficient conditions for these approximate solutions via nonlinear scalarization without any convexity assumptions. Our results correct the mistakes of several existence results. And some examples are given to illustrated the main results.

Key words:multiobjective programming problems, approximate quasi efficient solutions, nonlinear scalarization

通讯作者：高英(1982-),博士,副教授,研究方向:最优化理论与方法.

作者简介：李小燕(1990-),硕士生,研究方向：多目标优化.

基金项目：国家自然科学基金(11201511);重庆市科委项目(cstc2015jcyjA00005);重庆市教委项目(KJ1500309).

收稿日期：2015-05-04.

DOI：10.3969/j.issn.1008-5513.2016.01.005

中图分类号：O221.6

文献标识码：A

文章编号：1008-5513(2016)01-0026-10