巴拿赫代数上锥b-度量空间中压缩映射不动点定理

张丽娟,薛西锋

(西北大学数学学院,陕西西安　710127)



巴拿赫代数上锥b-度量空间中压缩映射不动点定理

张丽娟,薛西锋

(西北大学数学学院,陕西西安710127)

摘要：在对巴拿赫代数上的锥度量空间的压缩条件研究的基础上,运用迭代和限制谱半径的方法,证明了巴拿赫代数上的锥b-度量空间的压缩映射不动点定理,将锥度量空间的压缩条件推广到巴拿赫代数上的锥b-度量空间中.

关键词：巴拿赫代数上的锥b-度量空间;迭代法;谱半径;不动点定理

1　引言

不动点定理是泛函分析中的重要内容之一,巴拿赫代数上的锥度量空间已经有很多成果,其中文献[1]利用迭代法给出了巴拿赫代数上锥度量空间中不动点定理,而文献[2]证明了在列紧的锥b-度量空间中的不动点定理,文献[3]提出了锥b-度量空间中压缩映射不动点定理.本文所研究的巴拿赫代数上的锥b-度量空间中压缩映射不动点定理是在巴拿赫代数上的锥度量空间以及锥b-度量空间的基础上的推广.

2　预备知识

定义2.1设X是非空集, A是巴拿赫代数, s≥1为给定的实数,假设映射d : X×X→A,对于任意的x,y,z∈X,满足:

(1)θ≤d(x,y)并且d(x,y) =θ当且仅当x = y;

(2) d(x,y) = d(y,x); (3) d(x,y)≤s(d(x,z) + d(z,y)),则称(X,d,s)为巴拿赫代数A上的锥b-距离空间.

定义2.2设A是含单位元巴拿赫代数,若x∈A,则x的谱半径

注2.1若r(x)＜1,则e−x可逆.

注2.2如果r(k)＜1,则‖kn‖→0 (n→∞).

定义2.3设(X,d,s)是巴拿赫代数A上的锥b-距离空间,映射T : X→X ,如果存在向量k∈P并且r(k)＜1,对于任意的x,y∈X,有d(Tx,Ty)≤kd(x,y),则T有不动点.

引理2.4[2]设A是巴拿赫代数,向量x,y,k∈A,如果x,y可交换,则下列式子成立:

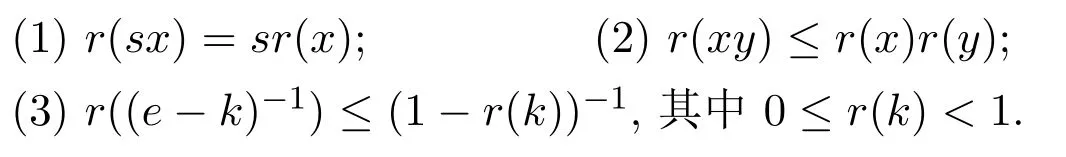
3　主要结果及其证明

定理3.1设(X,d)是巴拿赫代数A上完备的锥b-距离空间,系数s≥1, P是A上的体锥,向量λi∈P,其中r(λi)＜1,i=1,2,3,4且,若映射T : X→X满足压缩条件d(Tx,Ty)≤λ1d(x,Tx) +λ2d(y,Ty) +λ3d(x,Ty) +λ4d(y,Tx),∀x,y∈X.则T在X上存在不动点,并且对于任意的x∈X,迭代序列{Tnx}收敛于该不动点,如果满足则T的不动点唯一.

证明给定x0∈X,令x1= Tx0,xn+1= Txn,则

即得(e−λ1−sλ4)d(xn,xn+1)≤(λ2+ sλ4)d(xn−1,xn),同理

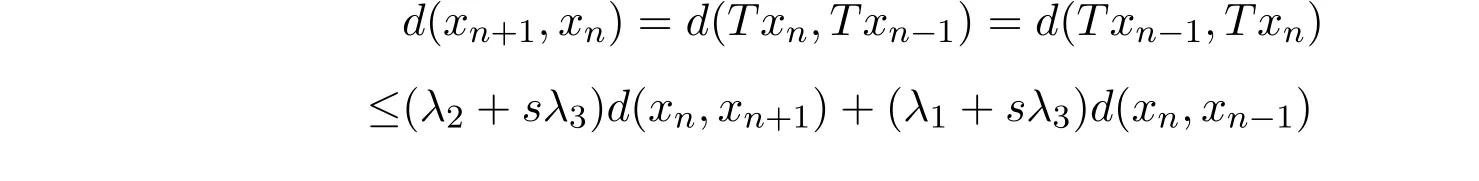
即得(e−λ2−sλ3)d(xn,xn+1)≤(λ1+ sλ3)d(xn,xn−1),综上可得

令r{[2e−λ1−λ2−s(λ3+λ4)]−1[λ1+λ2+ s(λ3+λ4)]} =λ,因此

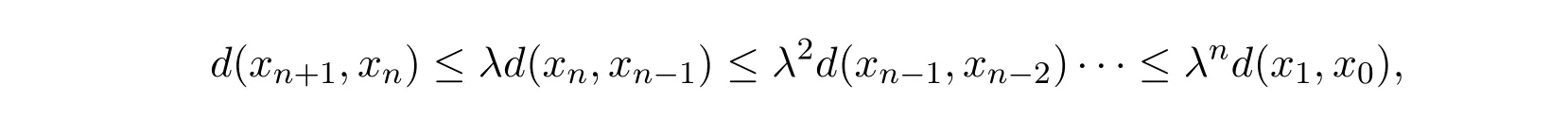
由r(λ)＜1,则‖λn‖→0 (n→∞),根据定理知xn为柯西点列,由X的完备性可得,存在x∗∈X,使得xn→x∗(n→∞).下面证明x∗为T的不动点.

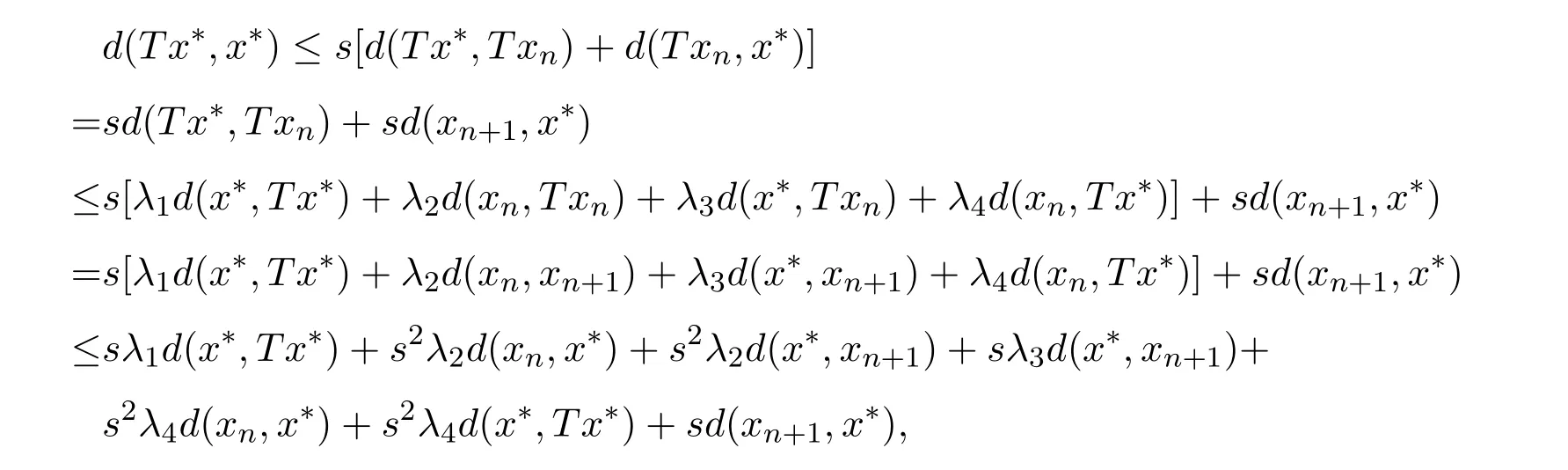
整理得(e−sλ1−s2λ4)d(x∗,Tx∗)≤(s2λ2+ s2λ4)d(xn,x∗) + (s2λ2+ sλ3+ s)d(x∗,xn+1).同理可证

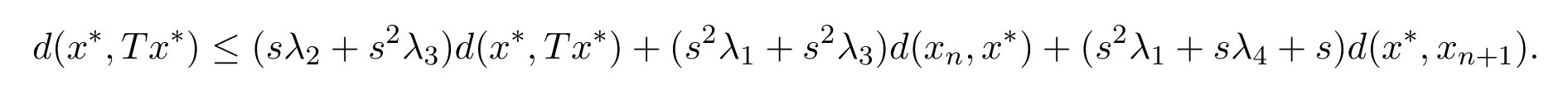
整理得(e−sλ2−s2λ3)d(x∗,Tx∗)≤(s2λ1+ s2λ3)d(xn,x∗) + (s2λ1+ sλ4+ s)d(x∗,xn+1),综上可得

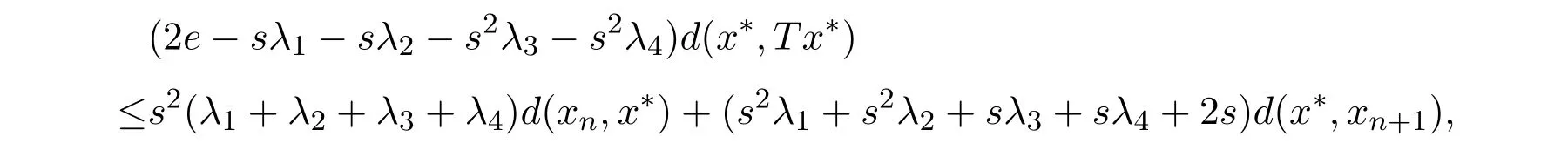
则d(xn,x∗)→θ(n→∞).即得d(x∗,Tx∗) =θ,即证x∗为T的不动点.

下面证明不动点的唯一性.不妨设y∗为T的另一个不动点,

定理3.2设(X,d,s)是巴拿赫代数A上完备的锥b-距离空间,系数s≥1, P是A上的体锥,其中α,β,γ,δ,ξ∈P.若映射T : X→X满足压缩条件:

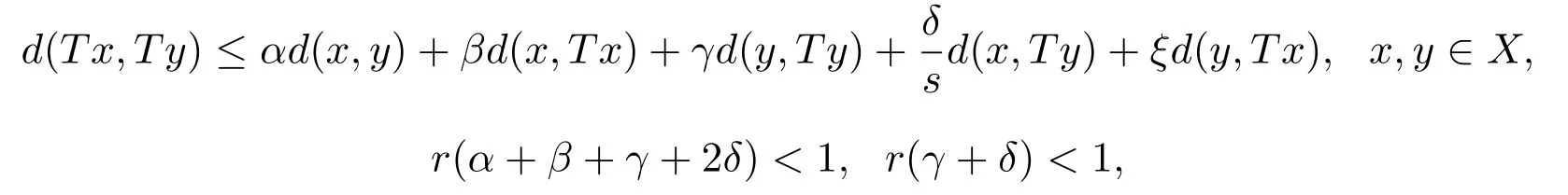
证明给定x0∈X,令xn= Txn−1,若对某个n,使得xn= xn−1,则xn−1为T的不动点,否则d(xn,xn−1)＞θ,

整理得(e−γ−δ)d(xn,xn+1)≤(α+β+δ)d(xn−1,xn).又因为r(γ+δ)＜1,则

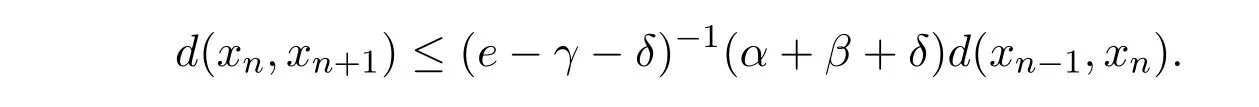
下面证明r[(e−γ−δ)−1(α+β+δ)]＜1.因为r(α+β+γ+2δ)＜1,故α+β+γ+2δ＜e, 得e−γ−δ＞α+β+δ而r(γ+δ)＜1,得γ+δ＜e, (e−γ−δ)−1(α+β+δ)＜e, 故r[(e−γ−δ)−1(α+β+δ)]＜1,根据定理知xn为柯西点列,由X的完备性可得,存在x∗∈X,使得xn→x∗(n→∞),由T的连续性知, Txn→Tx∗(n→∞),即

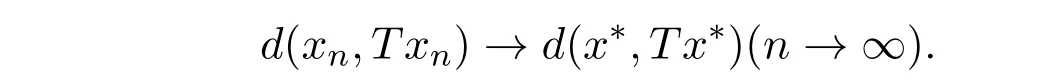
下面证明x∗为T的不动点.

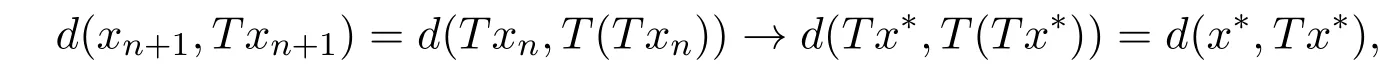
若Tx∗= x∗,则x∗为T的不动点,否则d(x∗,Tx∗)＞0,

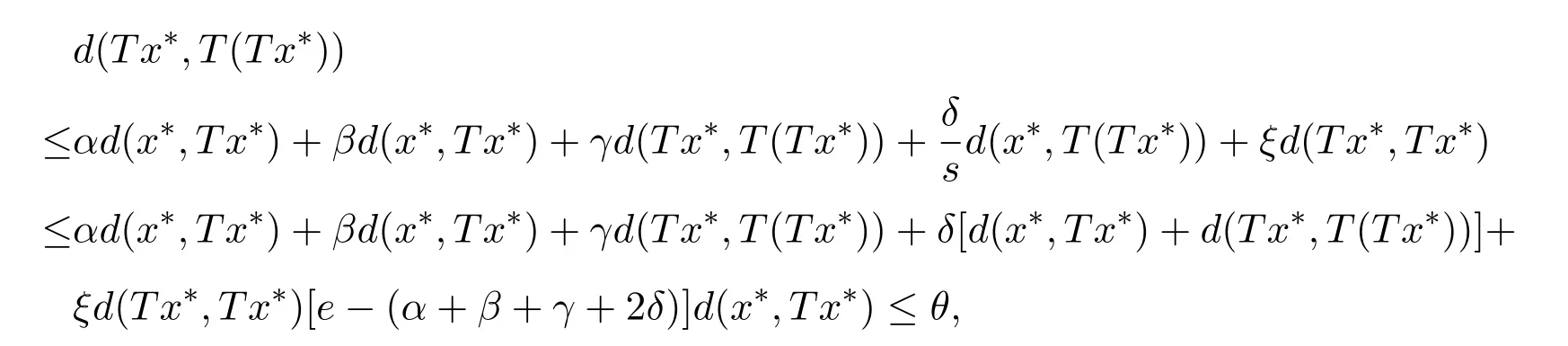
由于d(x∗,Tx∗)＞θ则e−(α+β+γ+ 2δ)≤θ与已知r(α+β+γ+ 2δ)＜1矛盾,即证Tx∗= x∗.下面证明不动点的唯一性.不妨设y∗为T的另一个不动点,

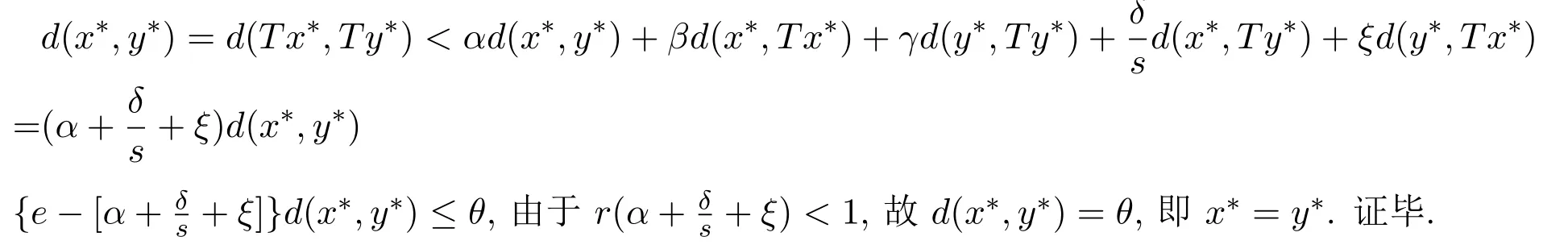
参考文献

[1] Xu Shaoyuan, Stojian Radenovic. Fixed point theorems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality [J]. 2013,320:1-12.

[2] Monica Cosentino, Peyman Salimi , Pasquale. Fixed point result on metric-type spaces [J]. 2010,102:1238-1249.

[3] Huang H, Xu S Y. Fixed point theorems of contractive mapping in cone b-metric spaces and applications [J]. Fixed Point Theory and Applications, 2013,112:1-10.

[4] Jankovic S, Kadelburg Z, Radenovic S. On cone metric spaces: a survey [J]. Nonlinear Analysis, 2011,4(7):2591-2601.

[5] Hussian N, Shah M H. KKM mappings in cone b-metric spaces [J]. Comput. Math. Appl., 2011,62:1677-1684.

[6] Kadelburg Z, Radenovic S. A note on various types of cones and fixed point results in cone metric spaces [J]. Asian J. Math. Appl., 2010,59:3148-3159.

2010 MSC: 60B12

Fixed point theorems of contraction mapping in cone b-metric spaces with Banach algebra

Zhang Lijuan , Xue Xifeng
(College of Mathematics, Northwest University, Xi′an 710127, China)

Abstract:This article is based on the taper on the Banach algebra space based on the study of the compression conditions, using the method of iteration and restrictions on the spectral radius, proves that the cone on the Banach algebra b-metric space compression mapping fixed point theorem, the taper in the space volume contractive conditions to promote the cone on Banach algebra b-metric space.

Key words:cone b-metric spaces with Banach algebras, spectral radius, iteration,fixed point theorems

作者简介：张丽娟(1989-),硕士生,研究方向：非线性泛函分析.

基金项目：陕西省自然科学基金(2012JM1017).

收稿日期：2015-10-04.

DOI：10.3969/j.issn.1008-5513.2016.01.008

中图分类号：O177.91

文献标识码：A

文章编号：1008-5513(2016)01-0055-05