AANA 随机变量序列的中心极限定理
2016-04-07张宇胡宏昌曾珍
张宇,胡宏昌,曾珍
(湖北师范学院数学与统计学院,湖北黄石 435002 )
AANA 随机变量序列的中心极限定理
张宇,胡宏昌,曾珍
(湖北师范学院数学与统计学院,湖北黄石435002 )
摘要:研究了渐近几乎负相依(简称为AANA)随机变量序列的渐近正态问题.在非常一般的条件下,得到了AANA序列的中心极限定理,推广了负相依(简称为NA)、独立随机变量序列的相应结论.
关键词:AANA序列;渐近正态性;中心极限定理
1 引言
由于随机变量独立性的假设在很多场合下不是很合适的,所以人们常常研究相依随机变量的情形.文献[1]中提出了如下渐近几乎负相依随机变量序列的概念.
定义1.1称{Xn,n≥1}为渐近几乎负相依(简称为AANA)随机变量序列,如果存在非负序列q(n)→0(n→0) ,对任意的n,k≥1都有
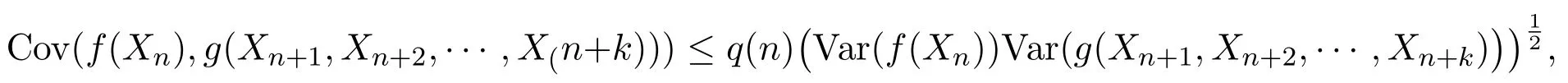
其中f和g是任何两个使上述方差存在且对每个变元均为非降的连续函数.称{q(n)≥n},为该AANA序列的混合系数.
AANA序列是包含独立列和NA序列的更为广泛的随机变量序列.显然,若随机变量序列是NA序列,则它们一定是AANA序列,反之不真[1].如:若令

其中η1,η2···为独立同分布N(0,1)随机变量, an≥0且an→0(n→∞),则{Xn,n≥1}是AANA序列,但不是NA序列.有关AANA序列的研究成果很多,文献[1]获得了Kolmgorov不等式和Marcinkiewcz-Zygmund强大数定律.文献[2]指出NA序列是AANA序列,其中混合系数满足q(n)≡0(n≥1).文献[3]建立了AANA序列部分和最大值的Rosenthal型不等式.文献[4]研究了AANA序列下移动平均过程的完全收敛性等.文献[5]得到了AANA序列加权和的强大数律.
随机变量的渐近正态性是统计学中研究的热门问题.文献[6]系统讲述了独立随机变量序列的中心极限定理.文献[7]讨论了非平稳同分布NA序列的渐近正态问题.文献[8]研究了NA误差下EV线性回归模型最小二乘估计的渐近正态性.文献[9]研究了NA误差下半参数回归模型的渐近正态性.其它相依误差情形见文献[10-12]等.然而,还未曾见到有文献研究AANA序列的渐近正态性.为此,本文研究了误差为AANA随机变量序列的渐近正态问题.在一般的条件下,得到了AANA序列的中心极限定理,推广了NA随机变量序列的相应结论.
2 主要结果
定理2.1设{Xn;n≥1}是同分布的AANA序列,满足条件:

存在严格上升的自然数序列{nk} ,对某0<α≤1满足


则有

其中{nk}表示严格上升的自然数序列1≤n1<n2<···,记
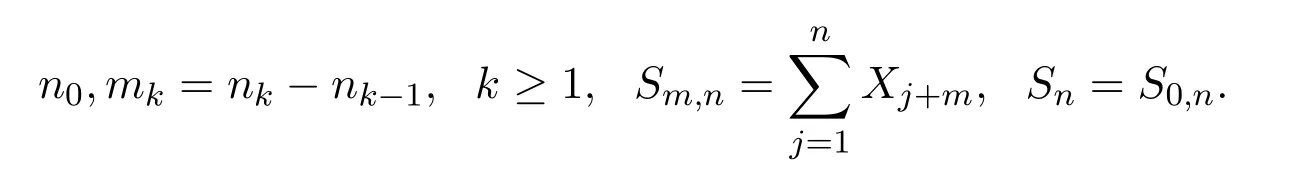
定理2.1的条件非常一般,很容易满足,文献[7]中的定理2.2满足定理2.1的条件.
推论2.1设在模型(1.1)中随机误差e1,e2,···,为同分布的NA序列,又满足条件(2.1)-(2.4),则(2.5)式成立.
由于独立序列是特殊的AANA序列,因此当误差为独立序列时,定理2.1仍然成立.
推论2.2设在模型(1.1)中随机误差e1,e2,···,为又满足条件(2.1)-(2.4),则(2.3)成立.
3 主要结果的证明
为证定理2.1,需要如下引理.
引理3.1[3]设{Xn,n≥1}是混合系数为{q(n),n≥1}的AANA随机变量序列, f1,f2,···全都是非降(或非增)的连续函数.则{fn(Xn),n≥1}仍是混合系数为{q(n),n≥1}的AANA随机变量序列.
引理3.2[3]设{Xn,n≥1}是期望为0的AANA随机变量序列,混合系数为{q(n),n≥1},则对于所有n和1<p≤2 ,存在只依赖于p的正数Cp,使得
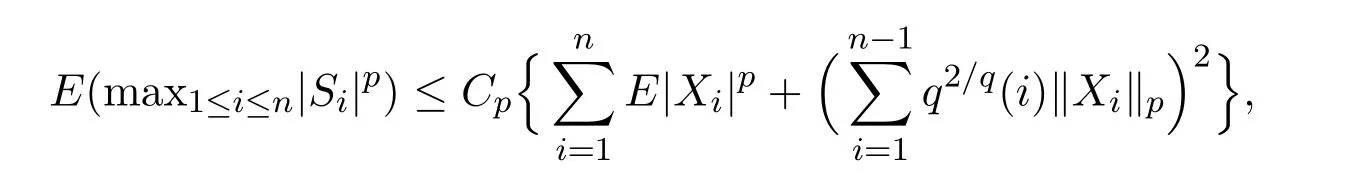
引理3.3[10]设X1,···,Xn为AANA变量,有EX2j<∞,则对任何实数λj,j = 1,···,n, 有

其中C为常数.
引理3.4[11]设X1,···,Xn为相互独立的随机变量,有EXj= 0,并对某0<α≤1 , 有E|Xj|2+α<∞,j = 1,···,n.又设f : R→R且二次可微,满足‖f′‖α≤∞则
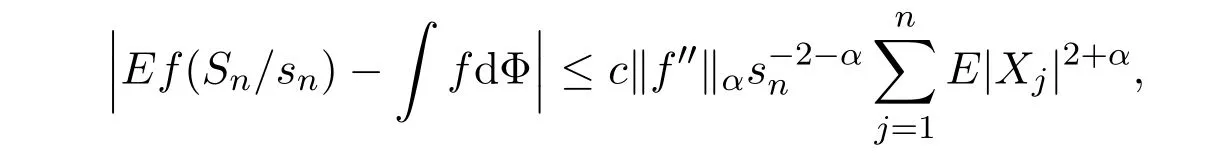
由于定理2.1的证明很长,下面先给出其证明框架.
第一,在条件(2.2)之下,当n充分大时,有ES2n≥cn.由条件(2.3)mk/nk→0(k→∞),并且对一切充分大的k,都有mk/nk−1≤1 ,结合引理3.2可知对∀ε>0 ,有
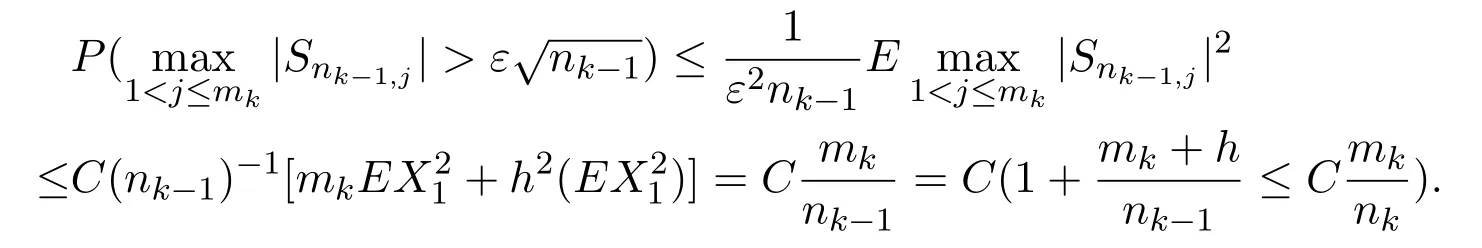
这表明为证(2.3)式,只需证明

第二,设{Xn;n≥1}是同分布的AANA序列,有EX1= 0.0<EX21<∞,对j⊆N令
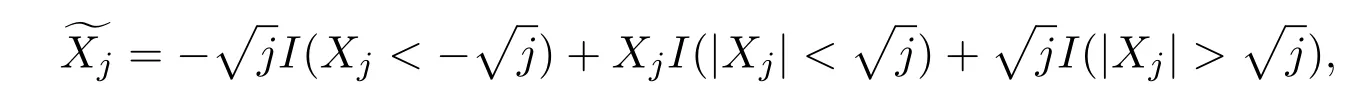
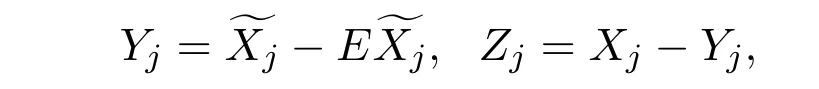
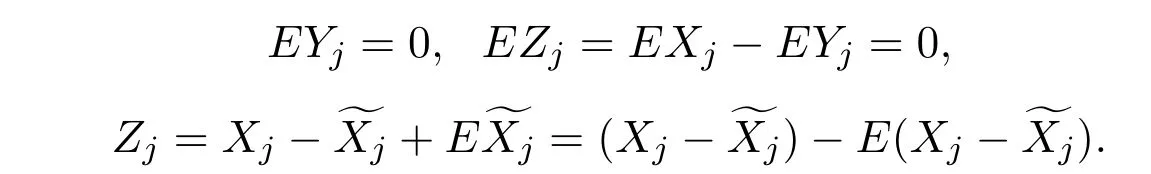
因此,由引理3.2
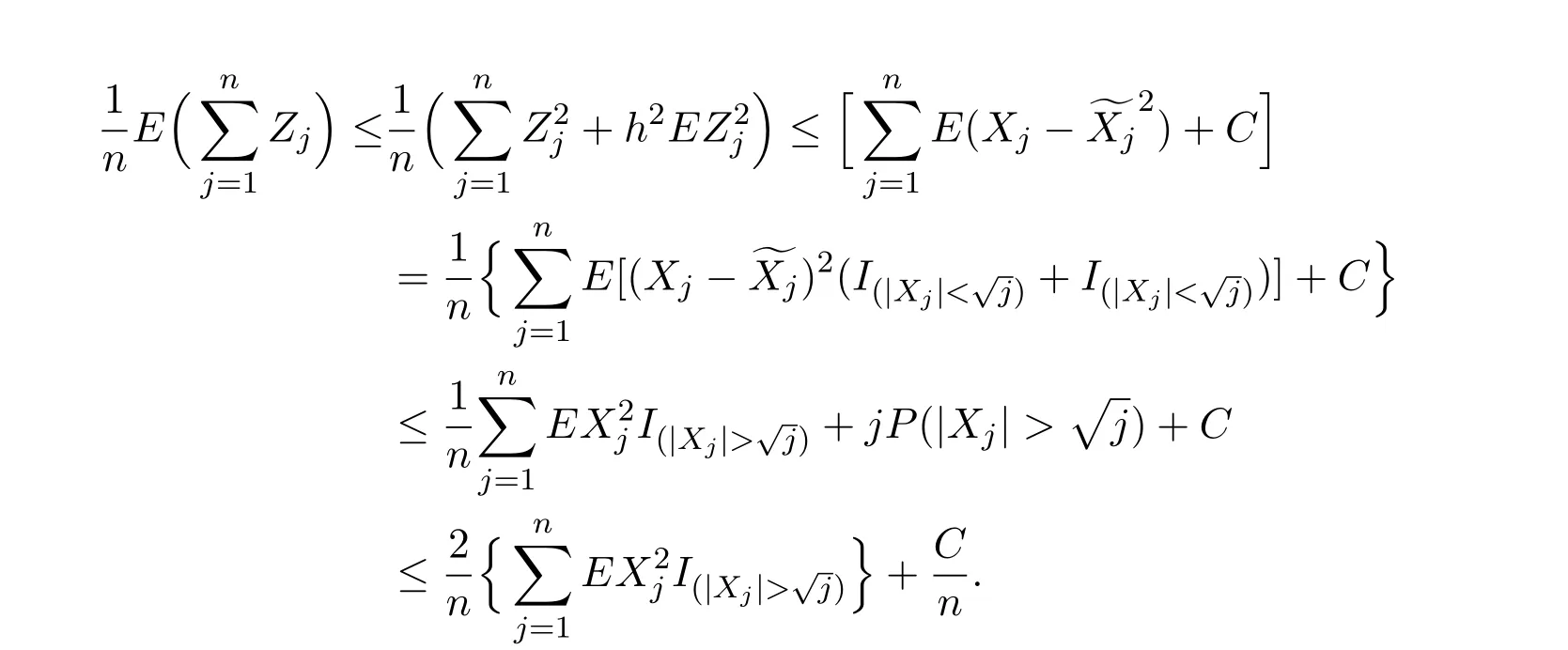
由EX21<∞,立知

从而对∀α>0 ,均有

又由于
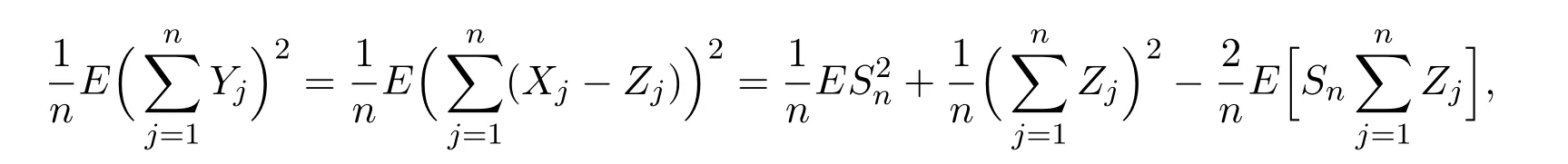
由Cauchy-Schwarz不等式及引理3.2
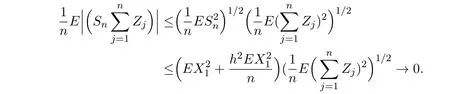
于是在引理3.4与(2.1)下,分别有

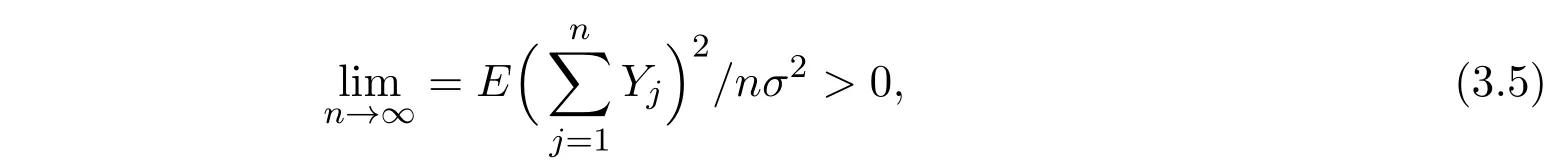
综合(3.1)-(3.5)式,即知为证(2.4)式,只需证明

第三,容易证明,在定理2.1中,只要

则有
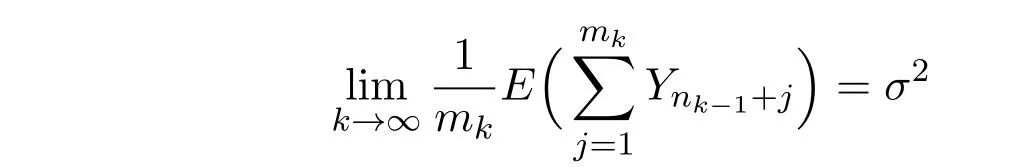
以上三点为定理的证明起到了简化作用.
定理2.1的证明记

则{Uk;k∈N}是AANA序列.现取一个独立随机变量序列{Vk;k∈N},使对每个k∈N, Vk均与Uk同分布.记
由前所述,为证定理2.1,只需证明(3.6)式,亦即要对∀u⊆R ,证明

记
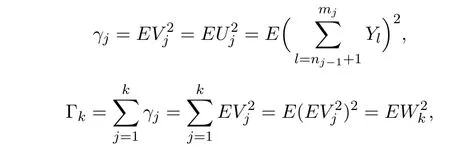
由(3.7)式知,γj/mj→σ2(j→∞).因此有
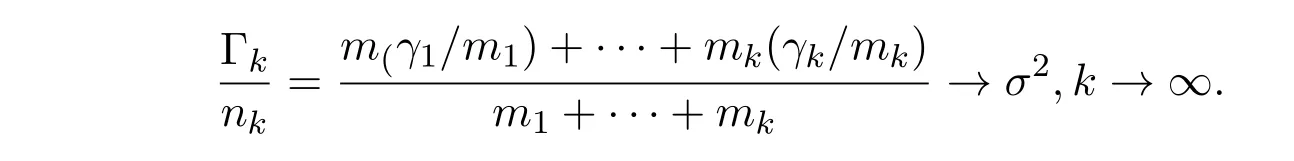
又由(3.4)式知

故而

这样一来,为证(3.8)式,只需对任何u∈R,证明
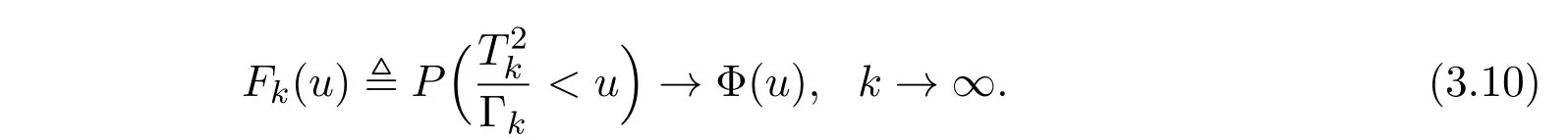
现在记
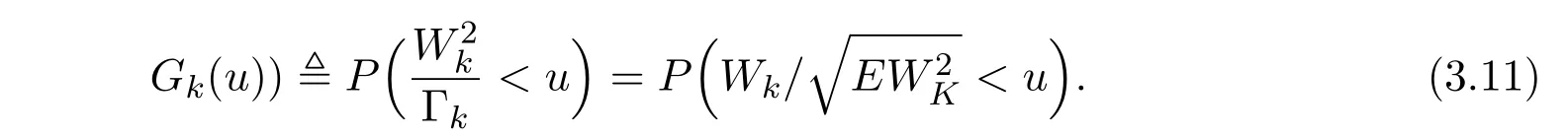
取定u∈R ,对每个ε∈(0,1] ,构造函数
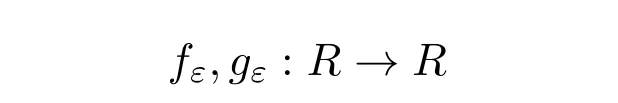
使它们均三次可微,并且
(1) 0≤fε≤1,0≤gε≤1;
(2)

(3)对定理条件(2.2)中的0<α≤1,有

其中‖.‖α的定义如下:
设f为定义在上的R函数,对0<α≤1,定义
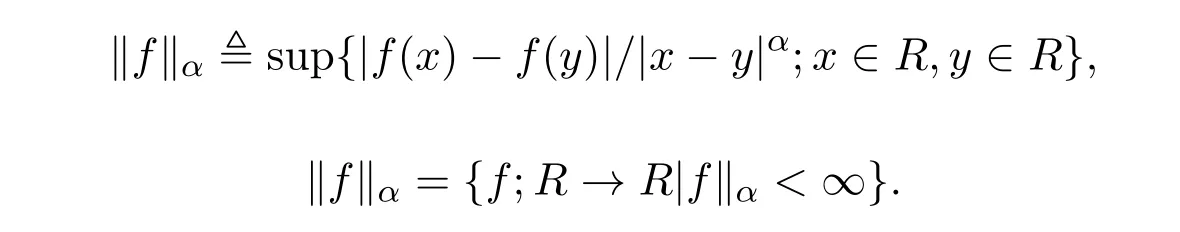
事实上,对ε= 1,易知满足上述条件的函数存在,对ε= 1 ,只要令
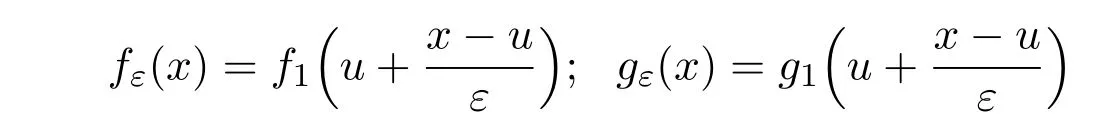
即可.不难看出,对任何0<ε<1,都有
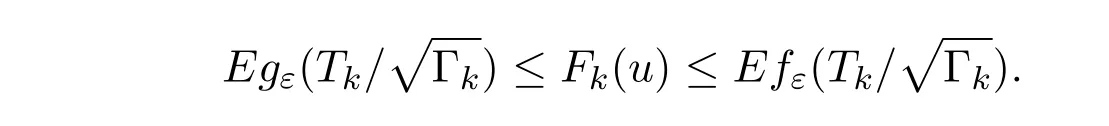
于是有
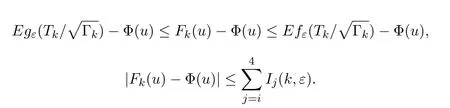
其中

因此为证(3.10)式,只需证明
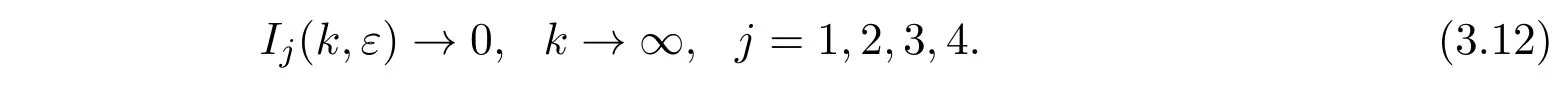
下面对j = 1,2与已取定的ε>0,证明(3.12)式.两种情形的证法类似,故仅证j = 1的情形.
由fε(x)的性质知,
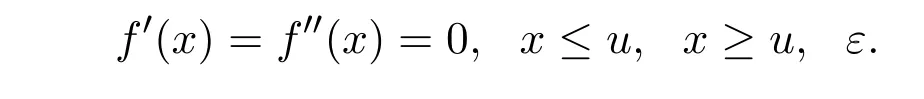
而由‖.‖α的定义及

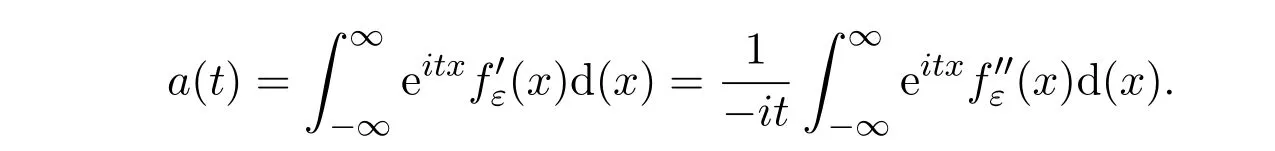
并且有

设Gk(u)由(3.12)式定义,令

则由V1,···,,Vk之间的独立性与Vj同Uj之间的同分布性有
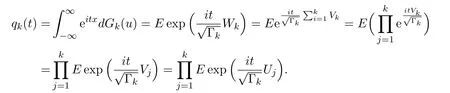
由引理3.3可知及定理2.1的条件(2.4)可知,

由(3.9)式知
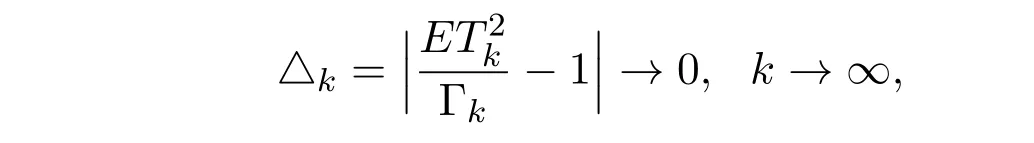
易见
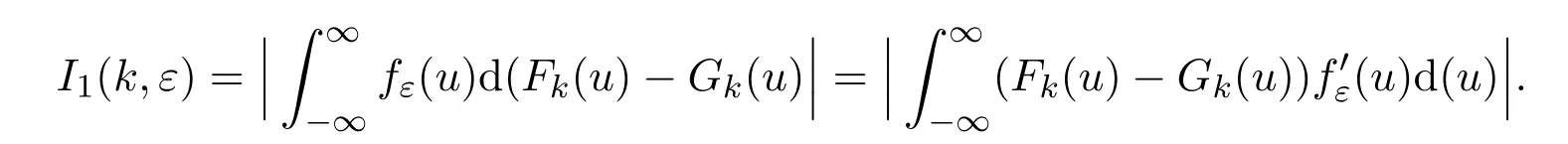
因此,由Parsevar[12]及(3.12)、(3.13)式知,

当△k= 0时,显然I1(k,ε) = 0;当△k≥0 ,记则由(3.12)式知
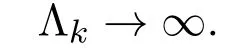
令
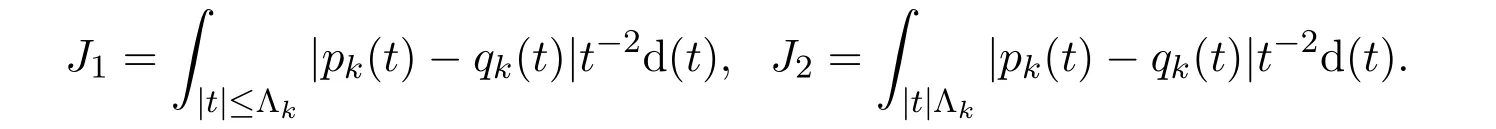
由(3.13)式知

由pk(t) ,qk(t)的定义知|pk(t)−qk(t)|≤2,因此

从而得

当j = 3,4时, (3.12)式的证明类似于文献[7]中定理2.1的证明,在此略.综上,定理2.1证毕.
参考文献
[1] Chandra T K, Ghosal S. Extensions of the strong law of number of Marcinkiewicz and Zygmund for dependent variables [J]. Acta Mathematical Hungarica, 1996,71(4):327-336.
[2] Chandra T K, Ghasal S. The strong law of number for weighted averages under dependence assumptions [J]. Journal of Theoretical Probability, 1996,19(3):797-809.
[3] Yuan DeMei, An Jun. Rosenthal type inequalities for asymptotically almost negatively associated random variables and applications [J]. Science in China Series A, 2009,52(9):1887-1904.
[4] Yang Wenzhi, Wang Xuejin, Ling Nengxiang. On complete convergence of moving average process for AANA sequence [J]. Discrete Dynamics in Nature and Society, 2012, Article ID863931, 24 pages, 1992,35(1):112-120.
[5] Chen Zhiyong. Strong laws of large numbers for weighted sums of asymptotically almost negatively associated random variables [J]. RACSAM, 2014, DOI 10.1007/s13398-014-0174-6.
[6]林正炎,陆传荣,苏中根.概率极限理论基础[M].北京:高等教育出版社, 1999.
[7]苏淳、迟翔.非平稳NA序列中心极限定理的一些结果[J].应用数学学报, 1998,21(1):9-21.
[8] Miao Yu. Asymptotic normality and strong consistency of LS estimators in the EV regression model with NA errors [J]. Stat Papers, 2013,54:193-206.
[9] Liang Hanying, Jing Bingyi. Asymptotic properties for estimates of nonparametric regression models base on negatively associated sequences [J].Journal of Multivariate Analysis, 2005,95:227-245.
[10] Newman C M. Asymptotic independence and limit theorems for positively and negatively dependent variables [J]. In: Y L Tong ed..Inequalities in Statistics and Probability,Institute of Mathematical Statistics, Hayward. CA., 1984.127-140.
[11] Butzer P L, Hahn L. General theorems on rates of convergence in distribution of random variables: General Limit Theorems [J]. J. Multivariate Anal., 1978,8:181-201.
[12] Liang hanying.Asymptotic normality of wavelet estimator in heieroscedastic model with mixing errors [J]. J Syst Sci Complex, 2011,24:725-737.
[13]佩特洛夫B B.独立随机变量之和的极限定理[M].苏淳,黄可明,译.北京:中国科技大学出版社, 1991.
2015 MSC: 60F15
Central limit theorems for AANA random sequence
Zhang Yu , Hu Hongchang , Zeng Zhen
(School of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)
Abstract:This paper discusses the asymptotic normality for asymptotically almost negatively associated (AANA,in short) random variables sequence. A central limit theorem for AANA random variables is obtained, and extend the corresponding conclusion of negatively associated (NA,in short) , independent random variables sequences.
Key words:asymptotically almost negatively associated sequence,asymptotic normality, central limit theorem
作者简介:张宇(1989-),硕士生,研究方向:应用概率统计.
基金项目:国家自然科学基金(11471105,11471223);
收稿日期:2015-07-11.
DOI:10.3969/j.issn.1008-5513.2016.01.006
中图分类号:O212.1
文献标识码:A
文章编号:1008-5513(2016)01-0036-09
