基于粒子群算法的捕食者-食饵模型的参数估计

刘利斌,刘翠萍,张永,王勇

(1.池州学院数学与计算机学院,安徽池州　247000; 2.西北核技术研究所,陕西西安　710024)



基于粒子群算法的捕食者-食饵模型的参数估计

刘利斌1,刘翠萍1,张永1,王勇2

(1.池州学院数学与计算机学院,安徽池州247000; 2.西北核技术研究所,陕西西安710024)

摘要：针对捕食者-食饵模型参数估计问题,基于三次Hermite插值多项式,提出了一种基于粒子群优化算法的高精度参数估计方法.数值仿真实验表明,本文提出的参数估计方法可以更精确地计算出相关参数.

关键词：捕食者-食饵模型;粒子群算法;参数估计

1　引言

在自然界中,不同种群之间存在一种相互依存又相互制约的生存方式.例如种群甲靠丰富的自然资源生存,而种群乙靠捕食甲为生,这就形成了捕食者-食饵系统.常用的捕食者-食饵模型具有如下形式:

其中, x(t)和y(t)分别表示食饵种群和捕食者种群在t时刻的数目; f[x(t)]和g[y(t)]分别表示食饵种群和捕食者种群在t时刻的增长率; p[x(t)]为捕食者种群对食饵种群的功能性反应函数, k为已知的常数.

对于捕食者-食饵模型的理论分析,一些学者已经进行了系统的研究[1-3].近年来,捕食者-食饵模型的参数估计问题越来越受到许多学者的关注.文献[4]研究了一类微分方程的参数反演问题,并提出了一种样条最小二乘算法.文献[5]考虑经典的捕食者-食饵模型的参数估计问题,给出了求解这类参数估计问题的信赖域方法.文献[6-7]讨论了捕食者-食饵模型的两阶段参数估计法,并得到了参数的估计值和置信区间.文献[8]首先利用三点的四阶差分格式对捕食者-食饵模型中的一阶导数进行了离散,并将其参数估计问题转化成一个无约束的优化问题,然后提出了一种混合加速粒子群算法来求解该优化问题.为了进一步提高捕食者-食饵模型参数估计的精度,本文基于三次Hermite插值函数,得出一个具有五阶精度的数值积分公式,并将该积分公式应用于捕食者-食饵模型数值离散,同时可得到相应的无约束优化问题.接着,利用基本的粒子群算法对该优化问题进行求解.与目前已有的算法相比,本文提出的参数估计方法的精度明显更高一些.

2　三次Hermite插值多项式与数值积分公式的构造

对于给定函数F : [x0,x1]→C[x0,x1],满足插值条件

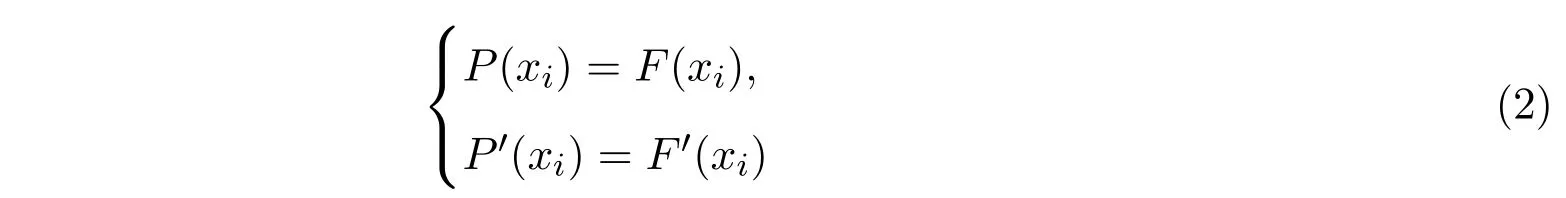
的三次Hermite插值多项式[9]可表示为:

其中

对于三次Hermite插值多项式(3),有如下的误差估计:

定理1.1[9]对于任意的实数x0, x1(x0＜x1),函数f(x)∈C4[x0,x1],若p(x)是三次的Hermite插值多项式,则对任意的x∈[x0,x1],都存在一个ξ∈[x0,x1],使得

进一步,由定理1可得如下数值积分公式:

其中ε∈[x0,x1].

3　捕食者-食饵模型的参数估计

考虑如下捕食者-食饵模型:

初始条件为x(t0) =α5, y(t0) =α6,其中αi(i = 1,···,6)是待求的参数.

显然,方程(6)为非线性常微分方程组,很难求出其解析解.因此,对于给定四个参数(α1,α2,α3,α4)和初始条件α5,α6,可采用数值方法进行求解.为了方便,称(α1,α2,α3,α4)为状态参数,初始值α5,α6为初值参数.

一般情况下,对于x(t), y(t)的一组测量数据

可将模型(6)中的参数估计问题转化为如下无约束的非线性优化问题:

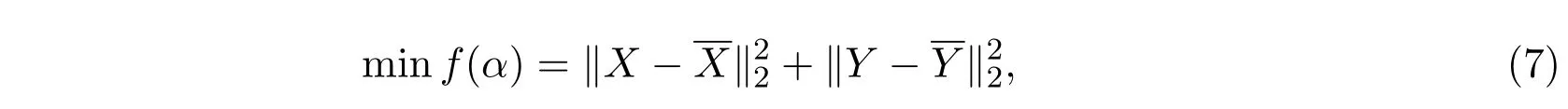
其中α= (α1,α2,α3,α4)为未知参数, X, Y为测量数据,为估计值.

接下来,为了得出目标函数(7)的具体表达式,利用(5)式对模型(6)进行离散,得

于是,目标函数(7)可转化为如下非线性优化问题

其中

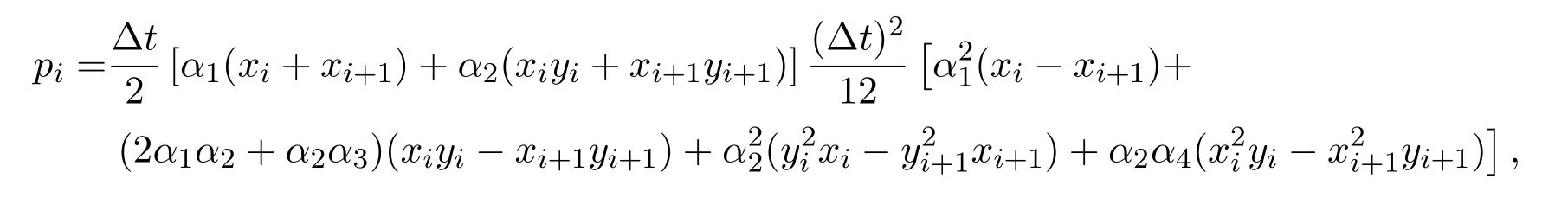
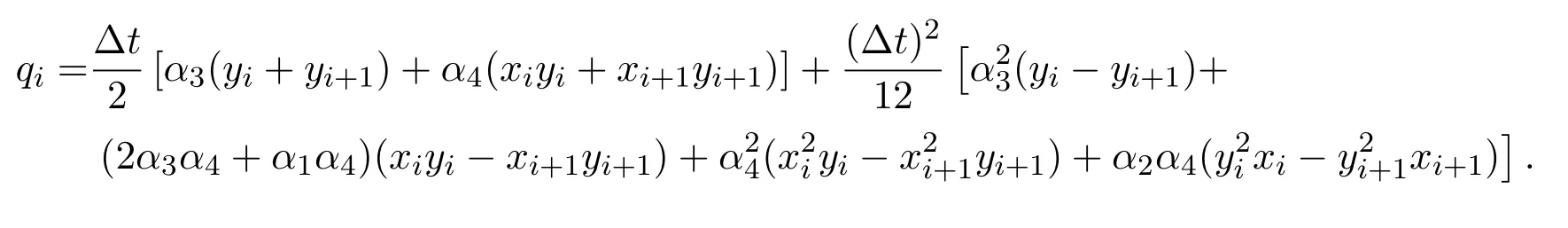
4　基本粒子群算法简介

粒子群算法(Particle Swarm Optimization),又称PSO算法,是由Eberhart博士和Kennedy博士在1995年提出的一种基于群体智能演化的计算技术[10].该算法最早是受到鸟群活动的规律性启发,进而利用群体智能建立起来的一个简化模型. PSO算法在对种群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题空间中产生无序到有序的进化过程,从而获得最优解.与遗传算法相比,它没有遗传算法的“交叉”和“变异”操作,它通过追逐当前搜索的最优值来寻找全局最优. PSO算法以其实现容易、精度高、收敛快等优点引起了许多学者的关注,并且在参数估计中展示了其优越性,见文献[11-15].粒子群算法迭代过程如图1所示.

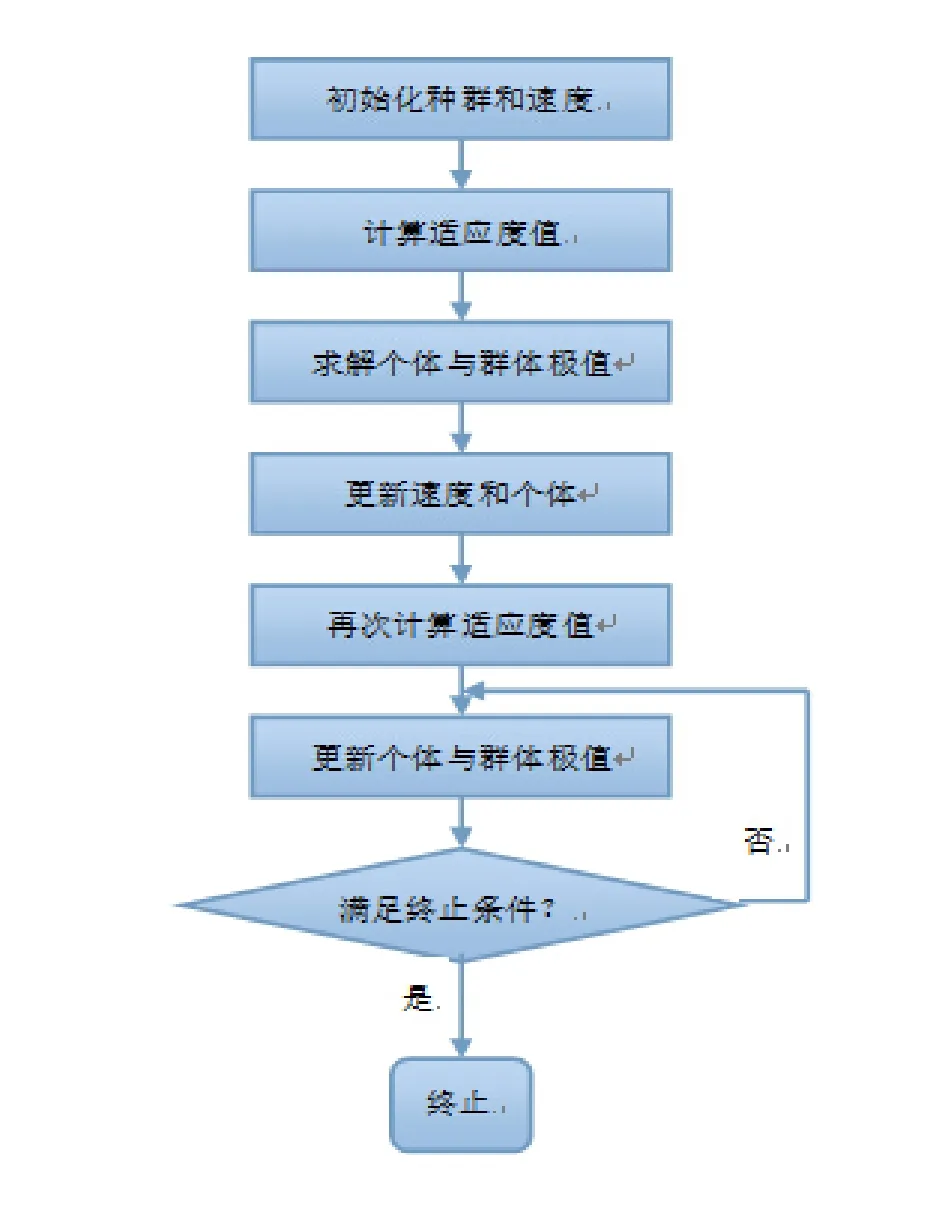
图1　PSO算法的流程图

5　数值实验与结果分析

在这里,以2006年全国研究生数学建模竞赛B题数据为例,验证本文方法的有效性,其中状态参数的真值为α= (2,−0.1,−10,1,13,72),时间区间[0,15],采样时间步长∆t = 0.1.另外,为了方便计算,将测量数据的第一组数据定为初值参数的估计值,即α5= 12.9622, α6= 72.1230.于是,在后面的计算结果中,只需计算α1,α2,α3,α4即可. PSO算法的参数设置为:最大迭代次数为50次,粒子数N = 200,加速常数c1= 1.2, c2= 1.2,状态参数范围αi∈[−11,11](i = 1,···,4).

接下来,采用粒子群算法对目标函数(8)进行求解,状态参数的计算结果见表1.同时,为了验证本文方法的优越性,表1中也列出了文献[7-8]的计算结果.在这里,表1中状态参数的误差采用如下式子进行计算,

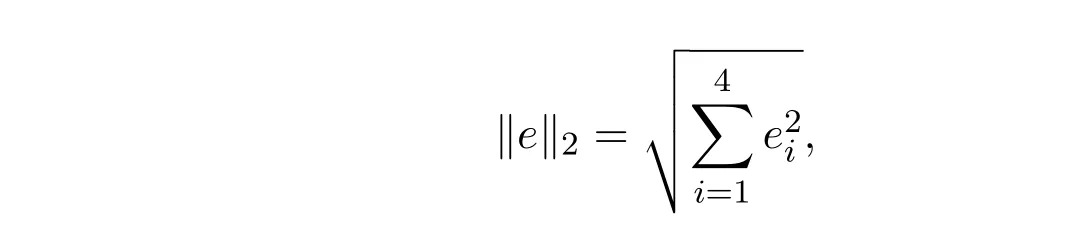
其中ei(i = 1,2,3,4)为各参数的估计值与真实值之间的差.

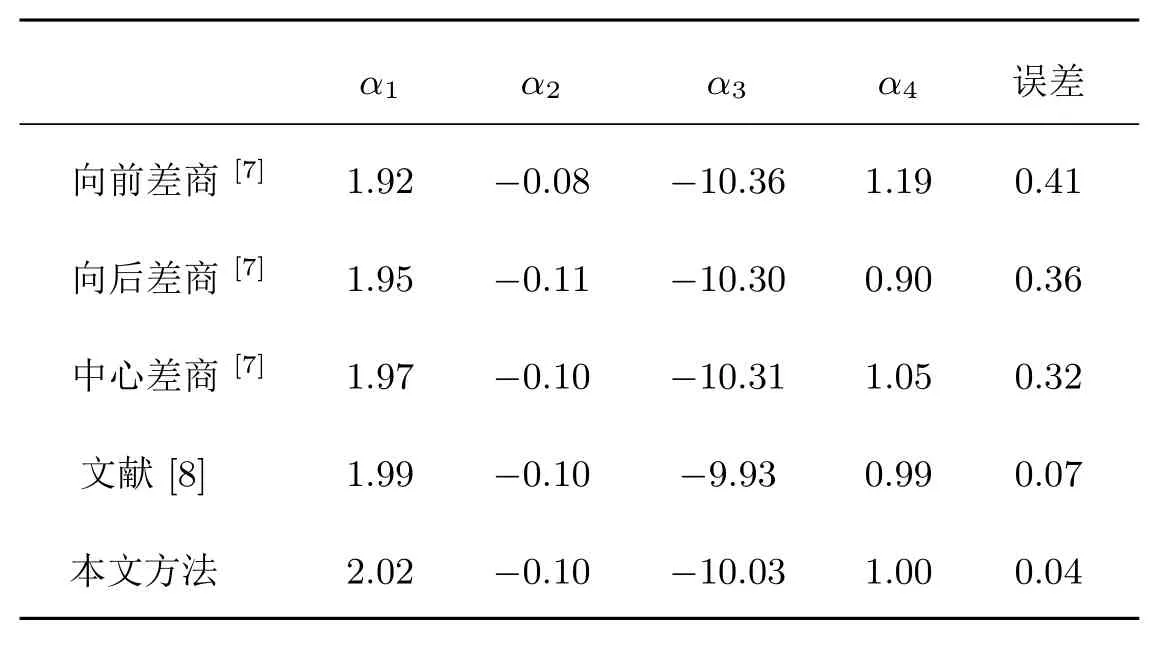
表1　不同算法计算得到的状态参数及误差

最后,将本文计算的结果代入模型(6),用Runge-Kutta法求得其数值并进行仿真,得出x(t)和y(t)的拟合曲线,如图2,图3所示.从图中可以看出,计算得到的结果和实际测量得到的结果是相当吻合的.

6　结论

对于捕食者-食饵模型的参数估计问题,本文首先结合三次Hermite插值多项式,提出了一个高精度的数值积分公式,并将其应用于捕食者-食饵模型的离散.值得一提的是该数值积分公式只需两个节点的函数值和导数值.然后,为了克服经典迭代优化算法对参数初值的依赖,采用了粒子群优化算法对捕食者-食饵模型的参数进行求解.数值实验表明本文提出的参数估计方法具有较高的精度.

图2　x(t)的测量与计算值的仿真结果比较

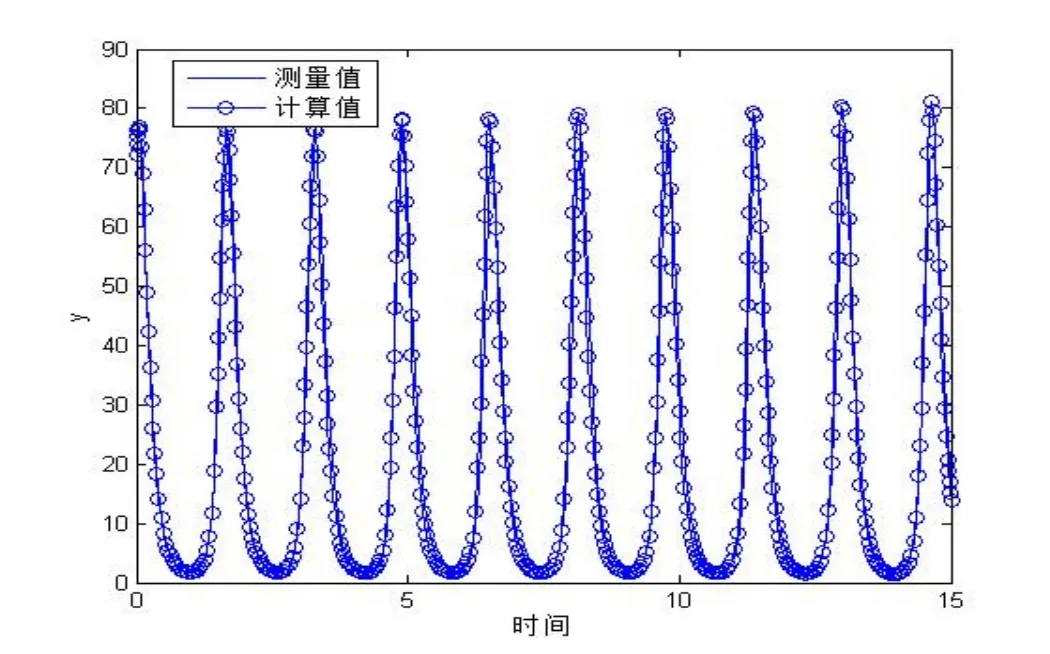
图3　y(t)的测量与计算值的仿真结果比较

参考文献

[1]王玲书.一个具有时滞和阶段结构的捕食-被捕食者模型的稳定性[J].高校应用数学学报, 2013,28(4):466-476.

[2]肖氏武,王稳地,金瑜.一类具有阶段结构的捕食者-食饵模型的渐进性质[J].生物数学学报, 2007,22(1):37-45.

[3]张亮亮,张丽娜.一类三种群捕食者-食饵模型中交错扩散导致的Turing不稳定[J].应用数学, 2014,27(1):82-87.

[4] Varah J. M. A spline least squares method for numerical parameter estimation in differential equations [J]. SIAM Journal on scientific computing, 1982,3:28-46.

[5] Jerome M B, Walmag, Eric J M, et al. A trust-region method applied to parameter identification of a simple prey-predator model [J]. Applied Mathematical Modeling, 2005,29(3):289-307.

[6]马新生,王来群,胡文玉.基于潜周期模型的两种群食饵-捕食者模型的参数估计[J].南昌大学学报(工科版) , 2008,30(2):134-137.

[7]马新生,翁瑾.两种群食饵-捕食者模型参数估计的数值微分法[J].南昌大学学报(工科版), 2010,32(1):741-796.

[8]曹怀火,李海燕,伏升茂.基于混合加速粒子群算法的捕食者-食饵模型参数估计[J].生物数学学报, 2013,28(3):553-557.

[9] Kress R. Numerical Analysis [M]. Graduate Texts in Mathematics, 181. New York. Springer-Verlag, 1998.

[10] Kennedy J, Eberhart R C. Particle swarm optimization [C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway. New Jersey：Institute of Electrical and Electronics Engineers, Inc., 1995:1942-1948.

[11]韩宁,尚朝轩.基于粒子群优化算法的LFM信号参数估计[J].计算机工程, 2012,38(4):176-178.

[12]燕振刚,胡贺年,李广.基于粒子群优化算法的Richards模型参数估计和算法有效性[J].计算机应用, 2014,34(10):2827-2830.

[13]李斌,李文锋.基于仿真的优化的粒子群算法参数选取研究[J].计算机工程与应用, 2011,47(33):30-35.

[14]郭建涛,王宏远,余本海.基于粒子群算法的调频信号参数估计[J].计算机应用研究, 2010,27(2):512-514.

[15]刘锦萍,郁金祥.基于粒子群算法的Logistic回归模型参数估计[J].计算机工程与应用, 2009,45(33):42-44.

2010 MSC: 65L12

Parameter estimation method for predator prey model based particle swarm optimization algorithm

Liu Libin1, Liu Cuiping1, Zhang Yong1, Wang Yong2
(1. College of Mathematics and Computer, Chizhou University, Chizhou 247000, China; 2. Northwest Institute of Nuclear Technology, Xi′an 710024, China)

Abstract:For the problem of predator prey model parameter estimation, a high accuracy parameter estimation method based on particle swarm optimization algorithm is proposed, which is based on the cubic Hermite interpolation polynomial. It is shown from the numerical results that the proposed method can be more accurate.

Key words:predator prey model, particle swarm algorithm, parameter estimation

作者简介：刘利斌(1982-),博士,讲师,研究方向:微分方程数值解法及智能计算.

基金项目：国家自然科学基金(11301044);安徽省优秀青年人才重点项目(2013SQRL095ZD);安徽省高校自然科学研究重点项目(KJ2015A213);安徽省大学生创新项目(AH201411306130).

收稿日期：2015-08-10.

DOI：10.3969/j.issn.1008-5513.2016.01.004

中图分类号：O175.14

文献标识码：A

文章编号：1008-5513(2016)01-0019-07