CVaR准则下双渠道供应链决策与博弈模型

赵　静，朱　昆

（天津工业大学理学院，天津　300387）

性质1最优零售价和零售商订购量随着直销价的增

证毕.由定理3，当v≥（pd- s）（F-1（α）+ L）+ t1时，

式中：



CVaR准则下双渠道供应链决策与博弈模型

赵静，朱昆

（天津工业大学理学院，天津300387）

摘要：考虑了包含一个风险厌恶的制造商和一个风险中性的零售商组成的双渠道供应链，运用博弈论和条件风险值（CVaR）准则，建立了3个博弈模型，即Nash博弈、制造商主导的Stacklberg博弈和零售商主导的Stacklberg博弈模型.通过比较和分析，得到了制造商风险厌恶度对制造商和零售商最优决策的影响以及价格敏感参数对最优决策的影响.最后，用数值算例验证了所建模型及分析的正确性，并分析了制造商风险厌恶度对制造商和零售商最大利润的影响.

关键词：双渠道供应链；CVaR准则；博弈；决策

供应链中存在着很多不确定因素，如顾客对产品数量和产品多样性偏好的需求不确定，供应商生产工艺变革以及生产能力变化的供应不确定，汇率变动，自然灾害和突发事件的外界环境不确定等，这些不确定因素会降低供应链配置的效率，给制造商和零售商的决策带来风险.决策者在面临风险时的态度一般分为3种：风险厌恶，风险中性和风险偏好.度量决策者风险态度的方法主要包括均值-方差，风险值（VaR）以及条件风险值（CVaR）. Markowitz 1952年提出的均值方差模型要求效用函数是二次的或收益满足正态分布，且计算复杂性高. William 1963年提出了风险值（VaR）模型，用于研究一定置信水平下某资产在持有期内预期的最大可能损失.但以VaR为目标函数的规划问题一般不是凸规划，求解困难；同时它忽略了分位点下的情况，即忽略了小概率事件可能造成巨额损失的情形.为此，文献[1]提出了CVaR准则，用于研究一定置信水平下低于分位数的平均利润.现实中，决策者在面临预期收益和损失时往往表现出风险厌恶的特性，因此，一些学者基于CVaR准则对供应链中某一决策层为风险厌恶时的库存，定价和协调等相关问题进行了研究[2-9]，如文献[2]研究了制造商和零售商均为风险厌恶者时供应链回购契约的优化和协调问题，文献[3]建立了零售商为风险厌恶者时单制造商-两零售商供应链的集中式和分散式决策模型以及相应的协调合同.然而以上文献研究的都是传统渠道某决策层风险厌恶的情形.

随着电子商务的迅猛发展，推动了企业供应链管理模式的变革.双渠道供应链管理模式被越来越多的企业所认可.双渠道供应链就是渠道参与者在原有传统销售渠道的基础上，开辟网络直销渠道的供应链系统.目前关于双渠道供应链参与者风险中性时的定价和协调问题研究较多，如文献[10-13].至于双渠道供应链中含风险厌恶参与者的决策问题，一些学者运用均值-方差法进行了研究，如文献[14]对风险厌恶制造商参与的双渠道供应链中的定价和协调问题进行了研究，文献[15-16]研究了制造商和零售商均为风险厌恶者时，双渠道供应链的定价与协调问题，文献[17]在零售商为风险厌恶下构建了单渠道和双渠道下的定价模型，讨论了零售商的风险厌恶度对两种供应链均衡策略的影响.运用CVaR准则研究的文献仅限于对最优订购策略的研究，如文献[18]，而定价和订购量联合决策的问题还没有研究.

本文基于CVaR准则，考虑了一个风险厌恶制造商和一个风险中性零售商组成的双渠道供应链中定价、产量和订购量联合决策问题和博奕问题研究.

1　问题描述及假设

考虑包含1个制造商和1个零售商的供应链，制造商以单位成本c生产1种产品，并通过2种销售渠道销售产品：一是传统零售渠道，即以单位批发价w批发给零售商，零售商再以单位零售价pr将产品销售给顾客；二是网络直销渠道，即制造商以单位直销价pd直接销售给顾客.

假设产品在直销渠道和零售渠道的需求函数分别为：式中：a表示市场基础；θ表示直销渠道销售所占市场的比例；（1 -θ）即是零售渠道销售所占市场的比例.参数θ1与θ2分别表示直销渠道需求对直销价格和零售渠道需求对零售价格的自身敏感系数，γ表示直销渠道需求对零售价格和零售渠道需求对直销价格的交叉敏感系数.假设β1>γ，β2>γ，这是因为价格对自身渠道需求的影响要大于其他价格对该渠道需求的交叉影响.随机变量εd和εr分别表示直销渠道需求风险和零售渠道需求风险，假设定义在区间[L，U]上，εi（i = r，d）的分布函数和概率密度函数分别F（x）和f （x），且E[εi] = 0，VaR[εi] <∞，由参考文献[6]可知，εi的失败率函数，对0 <α< 1，α-失败率函数.令di（pd，pr）= E[Di]表示期望需求，i = r，d.

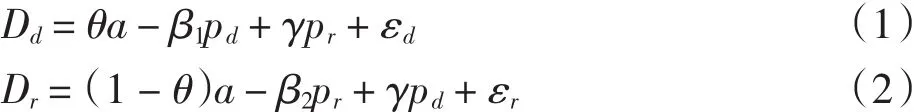
本文假设制造商和零售商均以各自利益最大化为目标进行决策，制造商决策产品的直销价pd和直销渠道的生产量qd，零售商决策产品的零售价pr和向制造商订购产品的订购量为qr对于未销售的产品，每单位剩余商品的净挽回损失为s，为避免平凡的情形，假设s < c.本文不考虑缺货损失.

基于以上描述和假设，零售商和制造商的利润函数分别建立如下：

式中：a∧b表示a与b中的较小值；a+表示a与0的最大值.

考虑制造商为风险厌恶偏好者，置信水平α下制造商的α- CVaR函数为：

式中：α（0 <α< 1）表示制造商的风险厌恶度，α越小，表示制造商对风险越厌恶，当α= 1时制造商为风险中性；为分位数.令

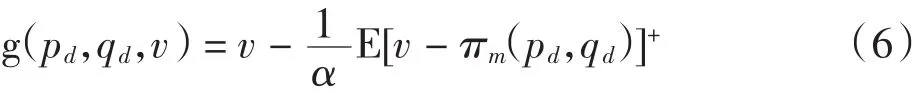
参考文献由[1]，（5）式等价于

式中：dr为零售渠道期望需求函数dr（pd，pr）的简写.

考虑零售商为风险中性，那么零售商的期望利润为：

2　模型建立及求解分析

现实中，由供应链节点企业规模大小差异、对市场信息掌控能力的不同以及议价能力的强弱差异导致了企业市场权力的不同，从而使得供应链成员间决策顺序也有所不同.本文利用博弈论，考虑分散式决策下的Nash博弈，制造商主导的Stacklberg博弈和零售商主导的Stacklberg博弈决策模型.

2.1 Nash博弈模型

考虑制造商和零售商市场权力相当的市场环境，制造商和零售商之间进行Nash博弈，他们同时进行决策.制造商决策直销渠道价格pd和直销渠道生产量qd，零售商决策产品零售价pr和订购量qr.该模型建立如下：

证明E[πr（pr，qr）]关于（pr，qr）的海塞矩阵为

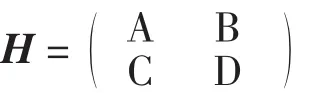
2.1.1零售商的反应函数

定理1当零售渠道需求风险的失败率h（x）=

式中：A = -2β2F（qr- dr）-（pr- s）f（qr- dr）β22；B = 1 -β2（pr- s）f（qr- dr）- F（qr- dr）；C = 1 -β2（pr- s）f（qrdr）- F（qr- dr）；D = -（pr- s）f（qr- dr）.

由定理1，零售商的期望利润函数存在唯一的最大值.令其一阶偏导数等于零，可得最优均衡解p*r，q*r.满足的条件由定理2给出.

定理2给定直销价pd和直销渠道生产量qd，当零售渠道需求风险的失败率h（x）>时，存在唯一的均衡零售价p*r和订购量q*r，满足以下条件：加而增加，即：

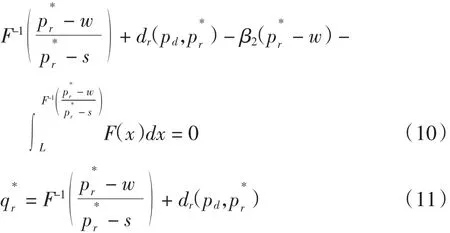
性质1最优零售价和零售商订购量随着直销价的增

2.1.2制造商的反应函数

定理3存在v*，使得CVaRα（πm（pd，qd））= g（pd，qd，v*）.

证明由（6）式得

其中t1=（w - c）qr+（pd- c）qd-（pd- s）（qd- dd），t2= （w - c）qr+（pd- c）qd.

（i）当v≤t1时，g（pd，qd，v）= v，故g（pd，qd，v）是关于v的单调递增函数；

（ii）当t1≤v≤t2时，g（pd，qd，v）是关于v的凹函数；

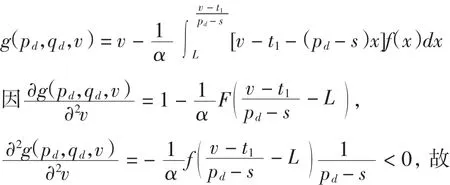
（iii）当v > t2时，

g（pd，qd，v）= v -[v - t1-（pd- s）x]f（x）dx -

结合（i）-（iii）可得g（pd，qd，v）在区间（t1，t2]上取得最大值，其最大值点为= s - c < 0，故制造商直销渠道生产量不会落在该区间.

证毕.
由定理3，当v≥（pd- s）（F-1（α）+ L）+ t1时，

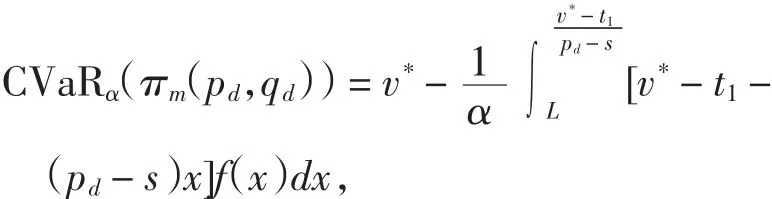
当v <（pd- s）（F-1（α）+ L）+ t1时，

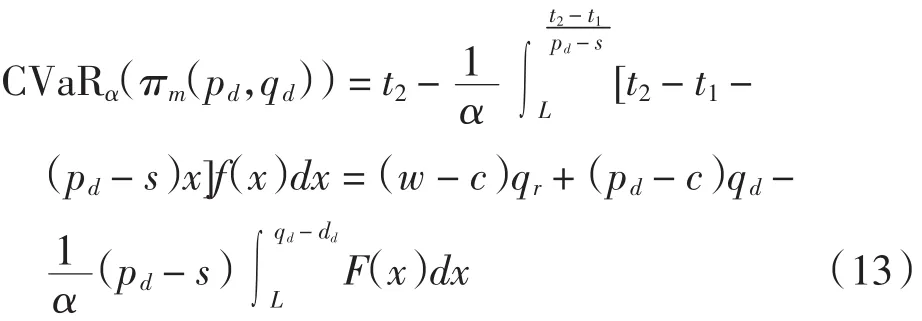
式中dd为直销渠道期望需求函数dd（pd，pr）的简写.

定理4当直销渠道需求风险的α-失败率hα（x）> 1αβ1（c - s）时，制造商的α-CVaR函数即（13）式是关于（pd，qd）的联合凹函数.

证明CVaRα（πm（pd，qd））关于（pd，qd）的海塞矩阵为：

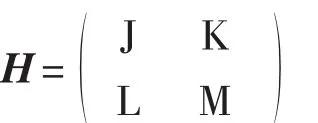
式中：

由定理4，制造商的α-CVaR函数存在唯一的最大值.令其一阶偏导数等于零，可得最优均衡解p*d，q*d.满足的条件由下面的定理5给出.

定理5给定零售价pr和订购量qr，当直销渠道需求风险的α-失败率易证当hα（x）=时，存在均衡直销价p*d和直销生产量q*d满足以下条件：

性质2最优直销价和直销渠道生产量随着零售价的增加而增加，即：2.1.3模型最优解及分析

联立（10）、（11）、（14）和（15）式，即可求得该博弈模型下的最优直销价p*dN，直销渠道生产量q*dN，零售价p*rN和零售渠道订购量q*rN.通过分析，得到以下性质：

（10）、（11）式和（14）、（15）式，分别对参数β1、β2和γ求偏导，得到参数β1、β2和γ对最优直销价，直销渠道生产量，零售价和零售商订购量的影响，可得性质4：

性质4（i）参数β1的敏感性分析：

（ii）参数β2的敏感性分析：

性质4（i）表明了直销价，直销渠道生产量，零售价和零售商订购量是随着直销价格敏感系数的增加而减少；（ii）表明了直销价，直销渠道生产量，零售价和零售商订购量随着零售价格敏感系数的增加而减少；（iii）表明了直销价，直销渠道生产量，零售价和零售商订购量都是随着交叉敏感系数的增加而增加.

2.2制造商主导的Stacklberg博弈模型

考虑这样的情形，市场风险厌恶的制造商较零售商拥有大的市场权力，是Stacklberg博弈的主导者，首先决策直销价pd和直销渠道生产量qd使其α-CVaR值达到最大，市场风险中性的零售商是Stacklberg博弈的跟随者，决策零售价pr和零售渠道订购量qr使其期望利润达到最大.该博弈模型建立如下：

采用逆向归纳法求解此模型，类似2.1.1节可知，零售商的反应函数p*r，q*r满足（10）和（11）式.

（13）式分别对pd和qd求一阶偏导数并令其等于零可得：

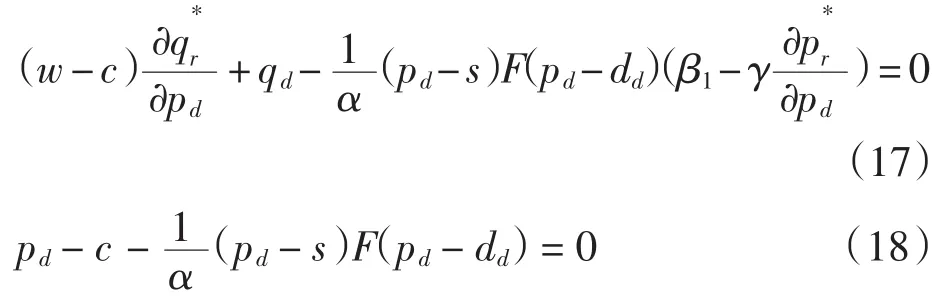
联立（17）和（18）式，求得制造商主导Stacklberg博弈决策模型下的最优直销价p*Md，直销渠道生产量q*d

M ，将求得的p*dM和q*dM代入（10）、（11）式，即可求得

最优零售价p*rM和零售商订购量q*rM.

性质5（i）最优直销价p*dM和零售价p*rM，随着风险厌恶度α的增加而减小，即：

（ii）最优直销渠道生产量q*Md随着风险厌恶度α的增加而增加，零售商订购量q*Mr随着风险厌恶度α的增加而减小，即：

性质5表明，当制造商越厌恶风险，那么制造商直销渠道的生产量将会减少，制造商会通过提高价格来增加利润.而零售商在了解到制造商的直销价和直销渠道生产量时，会因为制造商提高直销价而相应的提高零售价，同时零售商会增加其订购量，使其可以获得更多的利润.

（17）式分别对β1、β2和γ求偏导数，结合性质1，得到参数β1、β2和γ对最优直销价，直销渠道生产量，零售价和零售商订购量的影响，可得性质6：

性质6在制造商主导的Stacklberg博弈模型中：

（i）参数β1的敏感性分析：

（ii）参数β2的敏感性分析：

性质6表明了直销价，零售价和零售商订购量分别随着直销价格敏感系数，零售价格敏感系数和交叉价格敏感系数的增加而减小，而直销渠道生产量随着三种敏感性参数的增加而增加.

2.3零售商主导的Stacklberg博弈模型

考虑一个市场，市场风险中性的零售商较制造商拥有较大的市场权力，是Stacklberg博弈的主导者，首先决策零售价pr和订购量qr使其期望利润达到最大，市场风险厌恶的制造商是Stacklberg博弈的跟随者，决策其直销价pd和直销渠道的生产量qd，使其α-CVaR值达到最大.该博弈模型建立如下：

采用逆向归纳法求解此模型，制造商反应函数p*d，q*d满足（14）和（15）式，（8）式两边分别对pr，qr求偏导数并令其为零，得：

联立（20）和（21）式，可以求出零售商主导的Stacklberg博弈决策模型下的最优零售价p*rR和零售商订购量q*rR，将求得的p*rR和q*rR代入（14），（15）式，即可求出最优的直销价p*dR和直销渠道生产量q*dR.

性质7（i）最优直销价p*dR和零售价p*rR随着风

（ii）最优直销渠道生产量q*Rd随着风险厌恶度α的增加而减小，零售商订购量q*Rr随着风险厌恶度α的增加而增加，即：

这是因为零售商是博弈的主导者，了解到制造商是风险厌恶决策者时，制造商越是厌恶风险，零售商会提高零售价，减小订购量.制造商为博弈的跟随者，在了解到零售商的决策后，制造商也会提高直销价，但是会增加直销渠道生产量，来增加自己的利润.

（20），（21）式分别对β1、β2和γ求偏导，结合性质2，得到参数β1、β2和γ对最优直销价，直销渠道生产量，零售价和零售商订购量的影响，可得性质8：

性质8零售商主导的Stacklberg博弈模型中：

（i）参数β1的敏感性分析：

（ii）参数β2的敏感性分析：

性质8表明，直销价，零售价和直销渠道生产量随着直销价格敏感系数，零售价格敏感系数和交叉价格敏感系数的增加而减小，而零售商订购量随着3种敏感性参数的增加而增加.

2.4模型的比较分析

本小节对2.1—2.3小节中Nash博弈模型，制造商主导的Stackelberg博弈模型和零售商主导的Stackelberg博弈模型所得性质进行比较分析.

将性质3、5和7汇总在表1中，得到3种博弈模型下风险厌恶度对最优决策的影响.通过分析，得到结论1.

表1　风险厌恶度α对最优决策的影响Tab.1 Influence of degree of risk aversionαon optimal decisions

结论1（i）Nash博弈模型下，最优直销渠道生产量和零售商订购量随着风险厌恶度的增加均单调递增，这与文献中的研究结果（决策变量随风险厌恶度的增加单调递增）相一致；在两种Stackelberg博弈下，最优直销渠道生产量和零售商订购量随着风险厌恶度增加而呈现出相反的趋势，并且主导者决策的最优量单调递增，跟随者决策的最优量单调递减.

（ii）Nash博弈模型下，最优直销价和零售价随着风险厌恶度的增加递增，两种Stackelberg博弈下，最优直销价和零售价随着风险厌恶度的增加递减.

将性质4，6和8汇总得到表2，得到参数β1、β2和γ对最优决策变量的影响.通过对表2进行比较分析，得到结论2.

表2　参数β1、β2和γ对最优决策变量的影响Tab.2 Influence of parametersβ1、β2andγon optimal decisions

结论2（i）自身价格敏感参数β1和β2对最优决策的影响是一致的，即Nash博弈下，最优直销价，直销渠道生产量，零售价和零售商订购量随着自身价格敏感系数的增加而递减；制造商主导的Stacklberg博弈下，最优直销价，零售价和零售商订购量随着自身价格敏感系数的增加而递减，而直销渠道生产量随着着自身价格敏感系数的增加而递增；零售商主导的Stacklberg博弈下，最优直销价，零售价和直销渠道生产量随着自身价格敏感系数的增加而递减，而零售商订购量随着自身价格敏感系数的增加而递增.

（ii）Nash博弈下，最优直销价，直销渠道生产量，零售价和零售商订购量都是随着交叉价格敏感系数的增加而递增；制造商主导的Stacklberg博弈下，最优直销价，零售价和零售商订购量随着交叉价格敏感系数的增加而递减，而直销渠道生产量随着交叉价格敏感系数的增加而递增；零售商主导的Stacklberg博弈下，最优直销价，零售价和直销渠道生产量随着交叉价格敏感系数的增加而递减，而零售商订购量是随着交叉价格敏感系数的增加而递增.

3　数值分析

运用数值分析来验证上述模型的可行性，进一步比较3种博弈之间的差异以及风险厌恶度对制造商和零售商最优决策和利润的影响.参数取值：s = 20，c = 40，w = 60，β1=β2= 0.6，γ= 0.1，θ= 0.6，a = 100，εi服从（-10，10）上的均匀分布（i = r，d）.根据风险厌恶度α的不同取值，分别得风险厌恶度对最优定价的影响、风险厌恶度对最优直销渠道生产量和零售商订购量的影响和风险厌恶度对制造商CVaR值和零售商期望利润的影响，如图1—图3所示.

图1　风险厌恶度对最优定价的影响Fig.1 Influence of degree of risk aversion on optimal prices

图2　风险厌恶度对直销渠道生产量和零售商订购量的影响Fig.2 Influence of degree of risk aversion on direct channel production and retailer's order

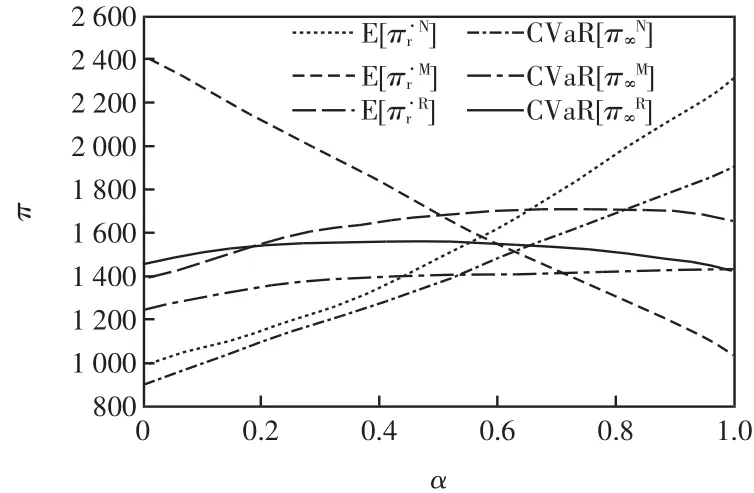
图3　风险厌恶度对制造商CVaR值和零售商期望利润的影响Fig.3 Influence of degree of risk aversion on manufacture's CVaR value and retailer's expected profit

（1）根据图1可知，制造商主导的Stacklberg博弈下的最优直销价和零售价分别大于和小于零售商主导的Stacklberg博弈下的最优直销价和零售价.造成这一现象的原因是，当制造商为博弈主导者的时候，制造商对市场信息有很高的了解程度，因此制造商会给出一个相对较高的消费者可以接受的直销价，同理当零售商为博弈主导者的时候，零售商对市场信息有很高的了解程度，因此零售商会给出一个相对较高的消费者可以接受的零售价.

（2）根据图2可知，①Nash博弈下的最优直销渠道生产量大于制造商主导的Stacklberg博弈下的最优直销渠道生产量，而Nash博弈下最优直销渠道生产量先小于后大于零售商主导的Stacklberg博弈下的最优直销渠道生产量.②Nash博弈下的最优零售商订购量大于零售商主导的Stacklberg博弈下的最优零售商订购量，而Nash博弈下的最优零售商订购量先小于后大于制造商主导的Stacklberg博弈下的最优零售商订购量.

（3）根据图3可知，①Nash博弈下零售商期望利润和制造商CVaR值都是随着风险厌恶度的增加而增加.②制造商主导的Stacklberg博弈下的零售商期望利润随着风险厌恶度的增加而先增后减，这是因为零售价随着风险厌恶度的增加而减少，零售商订购量随着风险厌恶度的增加而增加，而零售价减小所损失的利润和零售商订购量增加所增加的利润之和是先增后减的；制造商主导的Stacklberg博弈下的制造商CVaR值随着风险厌恶度的增加而先增后减，这是因为直销渠道利润增加的幅度先是大于后小于零售渠道利润减少的幅度.③零售商主导的Stacklberg博弈下的零售商期望利润随着风险厌恶度的增加而减少，制造商CVaR值是随着风险厌恶度的增加而增加的. ④Nash博弈下零售商期望利润随着风险厌恶度的增加先小于后大于制造商和零售商分别主导的Stacklberg博弈下零售商期望利润，制造商主导的Stacklberg博弈下的零售商期望利润随着风险厌恶度的增加而先小于后大于零售商主导的Stacklberg博弈下的零售商期望利润.⑤Nash博弈下制造商CVaR值随着风险厌恶度的增加而先小于后大于制造商和零售商分别主导的Stacklberg博弈下的CVaR值，制造商主导的Stacklberg博弈下的CVaR值随着风险厌恶度的增加而先大于后小于零售商主导的Stacklberg博弈下的CVaR值.

4　结论与展望

本文讨论了CVaR准则下双渠道供应链的决策和博弈问题.分析了风险厌恶度对3种博弈最优决策的影响，结果显示：①Nash博弈下，直销价，零售价，直销渠道生产量和零售商订购量是随着制造商风险厌恶度的增加而增加.②在制造商主导的Stacklberg博弈和零售商主导的Stacklberg博弈下，直销价和零售价都是随着制造商风险厌恶度的增加而减小的.③制造商Stacklberg博弈下的直销价和零售价分别大于和小于零售商Stacklberg博弈下相应的价格.最后通过数值分析，比较了风险厌恶度对制造商CVaR值和零售商期望利润的影响，以及三种模型间的差异.

关于双渠道供应链中风险的问题，还有待深入研究.一方面，文中假设批发价是外生变量，如果是内生变量结果会有什么不同；另一方面，文中考虑零售商是风险中性的，如果零售商也是风险厌恶时，上述结论是否仍成立.这些问题在今后将得到进一步研究.参考文献：

[1] ROCKAFELLAR R T，URYASEV S. Optimization of conditional value-at-risk[J]. Journal of Risk，2000，2（3）：21-42.

[2]闻卉，曹晓刚，黎继子.基于CVaR的供应链回购策略优化与协调研究[J].系统工程学报，2013，28（2）：211-218.

WEN H，CAO X G，LI J Z. Research on buy-back policy optimization and coordination of closed-loop supply chain based on CVaR [J]. Journal of Systems Engineering，2013，28（2）：211-218（in Chinese）.

[3]徐兵，贾艳丽，刘露.基于CVaR准则的单生产商两零售商供应链决策模型与协调[J].山东大学学报：理学版，2013，48（7）：101-110. XU B，JIA Y L，LIU L. The decision models and coordination of supply chain with one manufacture and two retailers based on CVaR criterion [J]. Journal of Shandong University（Natural Science），2013，48（7）：101-110（in Chinese）.

[4]许明辉，于刚，张汉勤.带有缺货惩罚的报童模型中的CVaR研究[J].系统工程理论与实践，2006，26（10）10：1-8. XU M H，YU G，ZHANG H Q. CVaR in a newsvendor model with lost sale penalty cost [J]. Systems Engineering-Theory & Practice，2006，26（10）：1-8（in Chinese）.

[5] CHEN X，SIM M，SIMCHI-LEVI D，et al. Risk aversion in inventory management[J]. Operations Research，2007，55（5）：828-842.

[6] CHEN Y，XU M H，ZHANG G. A risk-averse newsvendor model under CVaR decision criterion[J]. Operations Research，2009，57（4）：1040-1054.

[7] XU X H，MENG Z Q，SHEN R. A tri-level programming model based on Conditional Value-at-Risk for three-stage supply chainmanagement[J].Computers Industrial Engineering，2013，66（2）：470-475.

[8] XIE G，YUE W Y，WANG S Y，et al. Quality investment and price decision in a risk-averse supply chain[J]. European Journal of Operational Research，2011，214（2）：403-410.

[9] GOTOH J，TAKANO Y. Newsvendor solutions via conditional value-at-risk minimization[J]. European Journal of Operational Research，2007，179（1）：80-96.

[10] CHUN S H，KIM J C. Pricing strategies in B2C electronic commerce：Analytical and empirical approaches [J]. Decision Support Systems，2005，40（2）：375--388.

[11] KURATA H，YAO D，LIU J J. Pricing policies under direct vs. indirect channel competition and national vs store brand competition [J]. European Journal of Operational Research，2007，180（1）：262-281.

[12] HUANG W，SWAMINATHAN J M. Introduction of a second channel：Implications for pricing and profits [J]. European Journal of Operational Research，2009，194（17）：258-279.

[13] DAN B，XU G，LIU C. Pricing policies in dual-channel supply chain with retail services [J]. International Journal of Production Economics，2012，139（2）：312-320.

[14]王虹，周晶.风险规避型供应商主导的双渠道定价与协调研究[J].软科学，2008，22（11）：10-12，22. WAHG H，ZHOU J. Coordination and pricing decision of dual channel with risk averse supplier [J]. Soft Science，2008，22 （11）：10-12，22（in Chinese）.

[15]王虹，周晶.竞争和风险规避对双渠道供应链决策的影响[J]．管理科学，2010，23（1）：10-17. WANG H，ZHOU J. Effect of competition and risk aversion on dual channel supply chain[J]. Journal of Management Science，2010，23（1）：10-17（in Chinese）.

[16] XU G Y，DAN B，ZHANG X M. Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract[J]. International Journal of Production Economics：Part A，2014，147（1）：171-179．

[17]曹文彬，左慧慧.零售商风险规避对制造商双渠道选择的影响[J].商业研究，2014，56（6）：20-26. CAO W B，ZUO H H. Influence of retailers risk aversion on manufactures dual channel selection[J]. Commercial Research，2014，56（6）：20-26（in Chinese）.

[18]徐兵，刘露. CVaR准则下双渠道供应链订货与信息搭便车行为[J].工业工程，2014，17（5）：99-107. XU B，LIU L . A study of the order and information free-riding behavior of dual-channel supply chain based on CVaR criterion[J]. Industrial Engineering Journal，2014，17（5）：99-107 （in Chinese）.

Decision and game models in a dual-channel supply chain under CVaR criterion

ZHAO Jing，ZHU Kun
（School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

Abstract：A dual-channel supply chain composed of a risk aversion manufacturer and a risk neutral retailer was considered，by using game theory and conditional value at risk（CVaR）criterion，three game models，i.e.，Nash game model，manufacturer-Stacklberg game model and retailer-Stacklberg game model were established. Through comparison and analysis，the effects of the degree of manufacturer′s risk aversion on the optimal decisions，and the effects of price sensitivity parameters on the optimal decisions were obtained. Finally，the correctness of the models and analysis was validated by a numerical example，and the effects of the degree of manufacturer′s risk aversion on the maximum profits of the manufacturer and the retailer were analyzed.

Key words：dual-channel supply chain；CVaR criterion；game；decision

通信作者：赵静（1977—），女，博士，副教授，硕士生导师，主要研究方向为供应链管理. E-mail：zhaojing0006@163.com

基金项目：国家自然科学基金项目（71301116，71371186）

收稿日期：2015-09-22

DOI：10.3969/j.issn.1671-024x.2016.01.015

中图分类号：F274

文献标志码：A

文章编号：1671－024X（2016）01－0075－08