基于球面保角映射理论的表面特征标记点匹配法

汤春明，牛百铃，李光旭

（天津工业大学电子与信息工程学院，天津　300387）



基于球面保角映射理论的表面特征标记点匹配法

汤春明，牛百铃，李光旭

（天津工业大学电子与信息工程学院，天津300387）

摘要：提出一种基于曲面参数化理论的半自动匹配方法.首先，选择任一样本数据作为参照模型，根据其表面几何特征手动标定特征标记点；其次，利用保角映射方法将全部样本数据映射到同一球形域，根据球面坐标对应关系实现在其他样本表面上特征标记点的自动标定；最后，利用迭代逼近点方法归一化特征标记点在空间的位置.实验考察了统计形状模型的通用性原则和专一性原则，并且比较了球面保角映射中不同约束条件对获得模型质量的影响.实验结果表明：利用球面保角映射3个基准点约束所得模型的专一性指标明显好于零质心约束方法，并且实验所需时间减少近50%.

关键词：球面保角映射理论；特征标记点匹配；统计形状模型构建；活动形状模型；图像分割

model；image segmentation

由于将对象形状信息作为先验知识，统计形状模型（statistical shape model，SSM）已广泛应用于计算机医学辅助诊断（computer aided diagnosis，CAD）领域.常见的统计形状模型包括点分布模型（point distribution module，PDM）[1]和概率地图集PA[2].其中，点分布模型由于表达简洁、鲁棒性强、丰富的显示算法支持而常被用于医学图像分割、结构分析、形状再现等.

点分布模型是一种用来描述目标轮廓的可变形数学模型.首先在样本图像的目标轮廓上选取特征标记点构成训练集，然后利用主成份分析法对其进行统计分析，得到点分布统计模型.该模型主要包括2部分：第1部分是特征点组成的平均值，即平均轮廓；第2部分是特征点的形变方式，即特征点相对于平均轮廓的整体变化趋势.形变范围通过模型参数的变化范围加以限制，避免任意变形的可能性.

在不同的样本图像的目标轮廓之间选择对应的，具有相同局部几何特征的特征标记点是关系点分布模型质量的关键要素之一[3].这种对应点的匹配，最简单的方法是在每个例子中选择一个起点，以同等的距离放置并且使每个边界或表面的点数目相等.该方法在文献[4]中提出，然而，这种等距离的放置方法并不能给出一个合理的分组对应，在训练集中等效点的相对位置可能有很大的不同.用这些点训练得到的统计形状模型质量较差.另一种方法是提取表面的某些几何特性，如曲率或脊线形状[5-6].这些功能之间的对应关系可以用一个通用的数值优化算法建立[7].但是这些参考局部特征方法不能达到全局最优.另一类是考虑全局优化策略，如球面谐波（SPHARM）映射[8]，重参数化方法[5，9].本文以脏器图像作为研究对象，使用重参数化方法，引入球面保角映射作为零亏格表面模型的映射域，并比较了在球面保角映射中的2个约束条件对获得模型质量的影响.

1　训练样本匹配

1.1匹配过程

本文方法为半自动方法.首先选择一个表面样本作为参照模型，在其表面手动标定特征标记点.然后将所有表面样本映射到同一球面域中，根据球面坐标位置关系，自动在其他表面上找出特征标记点位置，如图1所示.“映射（mapping）”是指三维肺部表面特征标记点映射到球形参数域，“放置（placing）”表示图1中特征标记点放置的步骤顺序.首先计算球面形映射，把三维肺部表面特征标记点映射到单位球形结构域中.假设形状的旋转变换可以独立完成.因此，根据曲面曲率的参数域分布，可以匹配设置参考模型的所有训练集.同时，参考映射到球形参数域特征标记点的模型，完成三维肺部训练集的对应关系.

图1　特征标志点匹配过程Fig.1 Outline of landmarks matching

1.2球面保角映射

许多脏器的形状是属零拓扑结构，即封闭无孔的表面或自相交.由于具有相同的拓扑结构，可以把一个封闭的零亏格表面调和映射到单位球面[10].如图2所示的三角网格曲面，假设K为简单复合体，u、v为顶点，euv为跨越u、v的边缘线.在三维空间表面的位置矢量r（u，v）通常被表示为

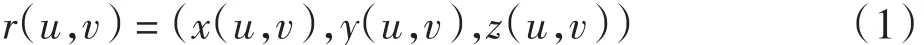
使用f来表示K上定义的分段线性函数.能量函数被定义为

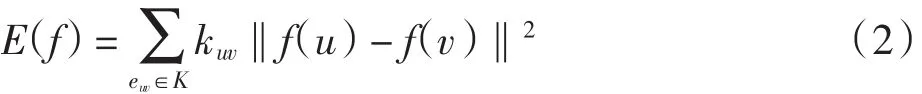
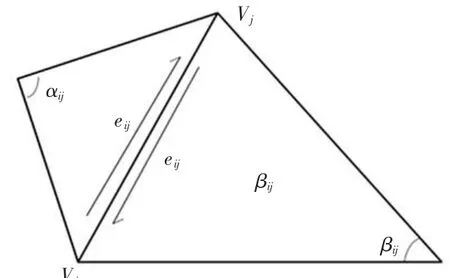
图2　三角网表面中相邻2个单元Fig.2 Triangular mesh surface adjacent two units

字符串常量kuv描述了表面和参数域之间的变化因素.改变它可以定义不同段的能量.如果kuv= 1，该段能量称为Tuette能量.字符串常量定义的谐波能量计算为

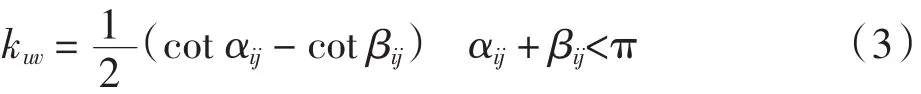
式中：αij和βij分别为相对于原三角曲面边缘的2个相对角度.

文献中有许多不同的方法来处理封闭零亏格表面，如谐波能量最小化、球面参数化和拉普拉斯等[11-12].球形映射是从一个封闭的零规格表面映射到单位球面的调和映射. Gu等[13]提出了一个快速下降算法使得到的谐波能量最小化和采用零质量中心约束指定映射结果.然而，通过使用快速下降法的共形映射的结构不是唯一的，会形成莫比乌斯带群.莫比乌斯带变换不同的约束将导致不同的映射结果.本文比较分别采用零质心约束和3个基准点约束的配准结果.

1.3球面保角映射到约束条件

本文将把三维肺部表面特征标记点映射到二维球面域.由于映射不是唯一的，球形映射有6个自由度并且所有球形的映射形式构成了莫比乌斯变换，称为莫比乌斯映射.它在复平面C中定义为

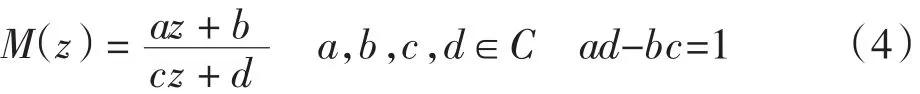
莫比乌斯变换是保形变换.确保共形映射是唯一的及算法的收敛性，需要添加额外的约束.在文献[13]中，Gu等使球形映射图的质心为原点：

式中：M2为网格M1的图；δM1为M1的区域元素.此约束确定训练样本是唯一的旋转，称此为零质心约束.

同时，另一种约束形状变化的方法是在表面固定3个基准点.给出3个不同的点Z1，Z2，Z3∈C，则莫比乌斯变换分别映射到（0，1，∞）

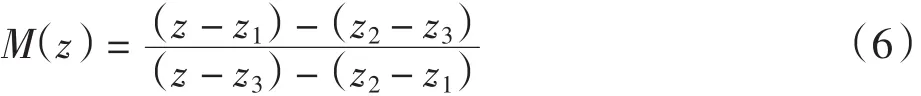
为了保证图形的对称性，选择P0、Pinit作为中心轴和表面的交叉点，Z1、Z3分别为它们的映射点. Z2是P1的复数坐标点，P1被选择为x轴和表面的交点，显示在图3（a）中.点P0，P1，Pinit分别映射到南极，CIO是北极.该算法如下：

输入：网格M1，能量误差阈值δE，在顶点上的3个基准点P0，P1，Pinit；输出：3个点P0，P1，Pinit分别被映射到南极，CIO和北极的球面共性图M2.

（a）计算高斯图.

（b）最小化Tuette能量得到Tuette映射.

（c）最小化共性能量得到球面共性映射.

（d）由公式（16）计算球面共形图的立体投影.

（e）Z1，Z2，Z3分别是P0，P1，Pinit的投影，计算全部顶点的高斯变换.

比较这2种约束下的匹配结果.当绘制球面上的经度线和纬度线时，可以在原始表面上进一步匹配，如图3（a）和（c）采用零质量中心约束的肺部，图3（b）和（d）是采用3个基准点约束的肺部.

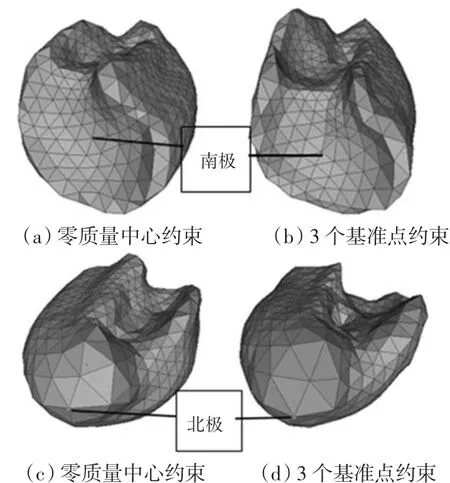
图3　莫比乌斯变换下不同的约束条件相同的肺部样本映射图Fig.3 Mobius transformation under same constraints of different lung sample map

1.4特征标记点的配准

图像配准实际就是通过分析待配准图像中存在的几何物体的形状，选择其中一种最合适的空间变换，使2幅图像中相对应部位可以一一对应起来[14].所以说，图像配准最基本的问题就是如何找到一种图像变换方法，这是一个寻找最优解的问题.

在前面的小节中，保角映射保证了原有的表面点的相对位置.找到坐标点的参考模型，首先，用参考模型映射的相同方式将训练样本映射到球形域，然后比较参考，根据球面坐标（θ，准）获得每一个点集相应的位置.然而，相应的位置通常不位于顶点，所以必须在物体表面周围的参考标记的位置找到近似的顶点.一种有序的顶点智能搜索方法是近邻搜索（NNS），这个搜索可以用树的特性迅速消除大部分的搜索空间，从而有效地进行.

1.5训练模型一致化

获得每个样本的特征标记点后，需要将这些样本的位置、大小在三维空间上进行统一.本文采用迭代逼近点法（Iterative Closest Point，ICP）实现.假设用表示空间第1个点集，第2个点集的对齐匹配转换为使下式的目标函数最小.

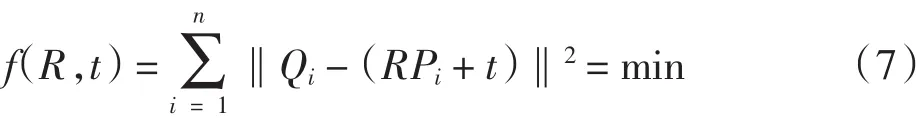
ICP算法本质上是基于最佳匹配方法的最小二乘法，通过重复点的集合，以计算出最佳的刚性变换过程，直到最后达到最优收敛准则. ICP算法主要是找到目标点集与参考点之间的旋转R和平移Τ变换，使得两匹配数据满足某种程度上的最优匹配.假设目标点集P的坐标及参考点集Q的坐标为，在第k次迭代中计算与点集P相对应的坐标为{QkQk∈R，i = 1，2，…，N}，计算P与Qk之间的变换矩阵并对原变换进行更新，直到数据间平均距离小于给定阈值子，即满足式（7）最小.步骤如下：

（1）在目标点集P中取点集Pki∈Pk；

（2）在参考点集Q中取对应点集Qki∈Qk，并计算使

（3）求得旋转矩阵Rk与平移向量Tk，使得

（4）计算

（5）如果dk+1大于或等于给定的子则返回到（2），直到dk + 1<子或迭代次数大于预设的最大迭代次数为止.

对于ICP每一次的迭代，最小化对应点的均方差均使得点集Pki离Qki更近，而Qki则是Pki在Qi的最近点.因此，每次的迭代会使得Pi离Qi更近.

2　实验部分

2.1实验数据

本研究采用人体肺部的CT图像作为研究对象.除生理器官本身的差异以外，受呼吸作用影响肺部的形变量较大.本研究采用的86例肺部图像数据由The Lung Image Database Consortium（LIDC）提供.实验比较了在物体表面均匀分布特征标记点方法和提案方法在模型质量上的差异.实验过程及结果如图4所示.

图4　实验过程及结果Fig.4 Experimental procedure and results

2.2评价指标

模型的通用性能力用来检测所生成的形状模型对合理的新形状实例表达的能力，即模型能够描述任一对象目标实例，不仅限于那些在训练集中出现的.它通常用leave-one-out算法执行.首先在N例训练中选出N-1例用于训练统计形状模型.然后用所得到的统计模型去和剩余一例进行匹配.此过程重复执行，其匹配误差的平均值作为此统计形状模型形状表达能力的评价指标.通用性能力被定义为一个关于形状特征矢量M的方程.例如，用2种方法获得的统计形状模型A和B，对于大多数的形状变量M有GA（M）≤GB（M），则表示A模型优于B模型.

模型的专一性能力是用来估计产生形状有效性的能力，即利用模型描述的形状皆为对象物体的合法实例.首先，利用统计形状模型产生一系列形状实例.然后，将产生的形状实例与训练集中的训练样本进行比较.则模型的专一性定义为

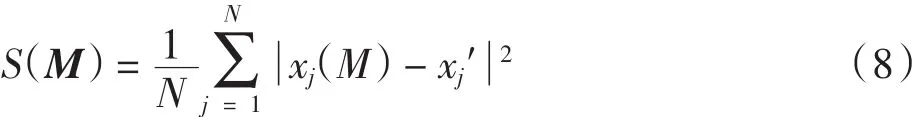
式中：xj代表训练样本产生的形状实例.同样，若SA（M）≤SB（M）则说明模型A更具专一性.关于模型通用性能力和专一性能力的实现方法参见文献[15].

2.3实验结果与分析

本文首先对86个肺部模型的通用性能力和专一性能力进行评价，结果如图5所示.由图5可知，通用性模型能够描述任意的目标实例，而不仅仅是那些训练集中出现的.专一性模型仅仅能够描绘有效的目标实例，有简洁性.

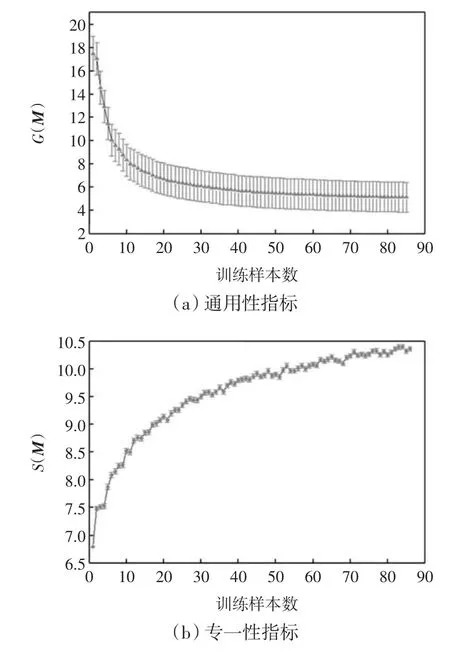
图5　模型质量的评价Fig.5 Quality evaluation model

再对20个肺部模型的通用性能力和专一性能力进行衡量，结果如图6所示.

图6的比较结果表明：虽然在模型通用性上，利用球面保角映射零质心约束得到的模型并没有明显的优越性，但是，利用球面保角映射3个基准点约束所得模型的专一性指标明显好于零质心约束方法，并且实验所需时间减少近50%.一般来说，特征标记点的匹配程度越高，特征点分布越“集中”，所获得的统计形状模型有效变化范围越小，即产生的样本实例越“紧凑”.因此，由于采用3个基准点约束方法获得的特征点匹配程度高于零质心约束方法，“模型专一性能力”也随之得到增强.

在计算效率上3个基准点约束方法也具有很好的可推广性.实践中，利用通用计算机（CPU：Xeon E5-1607 v2，内存：8 G）完成一例表面数据配准的执行时间通常少于30 min.

图6　模型质量的比较结果Fig.6 Comparison of results of model quality

3　结语

自动进行表面模型的特征标记点匹配是建立统计形状模型的第一步.本文提出了利用表面变量化方式和球面保角映射来实现三维三角网表面的特征标记点匹配问题.本研究利用表面数据的局部平均曲率和形状模型的紧致性特性作为对应特征的选取原则.由于3个基准点约束方法综合考虑了形状的局部特性和整体特性，优化过程具有一定的稳定性来抑制优化算法的局部极小问题.

此外，标记点的数目会影响模型表达能力，本文用1 069个标记点来表示一个肺部图形，如果采样点数目进一步增加，模型会有表达能力上的提高，后续工作是增加标记点个数，提高模型的表达能力.

参考文献：

[1] COOTES T F，TAYLOR C J. Statistical models of appearance

for medical image analysis and computer vision [C]//Medical Imaging 2001. [s.n.]：International Society for Optics and Photonics，2001：236-248.

[2] PARK H，MEYER C R，HYUNLIN PARK，et al. Construction of an abdominal probabilistic atlas and its application in segmentation [J]. IEEE Trans on Medical Imaging，2003，22 （4）：483-492.

[3] SHEFFER A，PRAUN E，ROSE K. Mesh parameterization methods and their applications [J]. Foundations and Trends in Computer Graphics and Vision，2006，2（2）：105-171.

[4] BAUMBERG A，HOGG D. Learning flexible models from image sequences[M]. Berlin：Springer Berlin Heidelberg，1994.

[5] WANG Y，PETERSON B S，STAIB L H. Shape-based 3D surface correspondence using geodesics and local geometry[C]// Computer Vision and Pattern Recognition，2000. Proceedings. [s.n.]：IEEE Conference on. IEEE，2000，2：644-651.

[6] BELONGIE S，MALIK J，PUZICHAJ. Shape matching and object recognition using shape contexts[J]. IEEE Trans on Pattern Analysis and Machine Intelligence，2002，42（4）：509-522.

[7] SCOTT G L，LONGUET-HIGGINS H C. An algorithm for associating the features of two images[J]. Proc of the Royal Society of London，1991，244（1309）：21-26.

[8] KELEMEN A，SZEKELY G，GERIG G. Elastic model-based segmentation of 3-Dneuroradiological data sets[J]. IEEE Trans. on Medical Imaging，1999，18（10）：828-839.

[9] MEIER D，FISHER E. Parameter space warping：Shape -based correspondence between morphologically different objects[J]. IEEE Trans on Medical Imaging，2002，21（1）：31-47. [10] GU X，WANG Y，CHAN T F，et al. Genus zero surface conformal mapping and its application to brain surface mapping[J]. IEEE Trans on Medical Imaging，2004，23（8）：949-958.

[11] GU X，WANG Y，YAU S T. Geometric compression using riemann surface structure [J]. Communications in Information and Systems，2004，3（3）：171-182.

[12] FLOATER M S，HORMANN K. Surface Parameterization：A tutorial and survey [C]//Advances in Multiresolution for Geometric Modelling Mathematics and Visualization. 2005：157-186.

[13]夏述高.三角曲面参数化若干问题研究[D].大连：大连理工大学，2011. XIA S G. Some issues triangle parametric surfaces[D]. Dalian：Dalian University of Technology，2011（in Chinese）.

[14] POWELL M J D. An efficient method for finding the minimum of a function of several variables without calculating derivatives [J]. The Computer Journal，1964，7（2）：155-162.

[15] DAVIES R H. Learning shape：Optimal models for analysing natural variability[D]. Manchester：Dissertation University of Manchester，2002.

Signature point matching method based on spherical conformal mapping theory

TANG Chun-ming，NIU Bai-ling，LI Guang-xu
（School of Electronics and Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China）

Abstract：A semi-automatic matching method based on surface parameterization theory is presented. Firstly，one of surface sample data as a reference model is selected. According to the geometric characteristics of surface，some landmark points are choosed manually. Then，all the sample data are mapped to the same sphere by the conformal mapping method. The landmark points on the other surface samples are completed automatically according to the positions corresponding to their spherical coordinates. Finally，to normalize the positions of landmarks in threedimensional space，the Iterative Closed Points method is utilized. The experiments measure the general principle and specificity principle of the model. Moreover，the influence on the point distribution model due to the different constraints of spherical conformal mapping method is compared. The results show that the specificity of the model based on spherical confomcal mapping theory is much letter than that of zero centroid constraint method，the time for the experiment is decreased by 50%.

Key words：spherical conformal mapping theory；signature point matching；statistical shape model building；active shape

通信作者：汤春明（1971—），女，教授，主要研究方向为图像处理与模式识别. E-mail：tangchunminga@hotmail.com

收稿日期：2015-09-01基金项目：天津市应用基础与前沿技术研究计划项目（14JCYBJC42300）

DOI：10.3969/j.issn.1671-024x.2016.01.011

中图分类号：TP311

文献标志码：A

文章编号：1671－024X（2016）01－0054－05