基于分数阶PID及内模原理的长行程直线电机控制系统设计

陈兴林，陈震宇

（哈尔滨工业大学控制科学与工程系，哈尔滨　150001）



基于分数阶PID及内模原理的长行程直线电机控制系统设计

陈兴林，陈震宇

（哈尔滨工业大学控制科学与工程系，哈尔滨150001）

摘要：为了对长行程直线电机进行精确伺服控制，提出了一种结合分数阶PID及内模控制原理的控制系统.以内模控制器作为电流环控制器、分数阶PID作为位置环控制器，在简化了控制器设计、降低调试难度的同时，保证了跟踪精度.最后，对长行程直线电机驱动的光刻机掩模台宏动台进行了仿真验证，验证了所提出的控制策略的有效性.

关键词：分数阶PID控制；内模控制；控制系统设计；直线电机；光刻机

长行程直线电机由于其驱动能力强、工作行程大的特点而被广泛应用于许多领域当中，其控制策略的研究也成为了一个研究热点[1-3].作为生产制造集成电路的最主要设备，光刻机是光、机、电一体化的尖端精密运动平台的代表，其中光刻机掩模台宏动部分在直线电机的驱动下实现承载硅片大行程运动，其精度要求需要达到微米级.为了达到要求精度，通常使用三环控制策略以在保证稳定性的同时能够提高系统的响应速度.但传统三环PID控制方法的控制精度无法达到要求，并且当电流环引入PID控制器后会提高电流环闭环等效模型阶次，从而造成速度环与位置环控制器参数设计困难的问题.

为了在降低控制系统设计难度的同时提高控制精度，本文提出了一种以内模控制器作为电流环控制器、分数阶PID控制器作为位置环控制器的控制策略，从而降低电流环闭环等效模型阶次、简化各环控制器设计；同时分数阶PID控制器的引入能够大幅度提高系统精度、提高控制系统性能.

1　控制方法

1.1分数阶PID

分数阶PID控制最早在1999年由Podlubny教授提出，他在著作《Fractional Differential Equations》中提出分数阶PIλDμ控制的基本结构[4].较普通PID控制而言，该控制器多了2个可调节参数，即积分阶次以及微分阶次滋.也因此，该系统可通过扩大参数整定范围获得更好的性能.另外，Podlubny教授还在著作中证明了其较传统PID而言的强鲁棒性[5-6].自此，分数阶PIλDμ得到广泛发展[7]，大量研究表明该理论比传统PID控制更能实现理想控制效果.

分数阶PIλDμ控制器传递函数为：

式中：KP、KI、KD分别为比例、积分、微分系数；姿>0、滋> 0分别为积分、微分阶次.

由于积分微分存在分数阶次，在仿真和实际运用中都不能直接使用固有模块，因此需要对分数阶因子进行近似公式推导计算，即用整数阶算子近似代替分数阶.本文选用最经典的Oustaloup算法逼近分数阶算子，在频率段内，可高精度实现分数阶微积分[8].

设工作频段为（ωb，ωh），在该频段内对分数阶算子进行近似计算.则Oustaloup递推滤波器传函为：

设r为分数阶算子的阶次，其中r<0时为积分阶次，r>0时为微分阶次.由上式，2N+1为滤波器阶次.则可表述成：

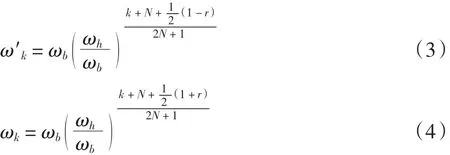
根据文献[8]中提出的改进Oustaloup算法，分数阶算子可以用式（5）近似：

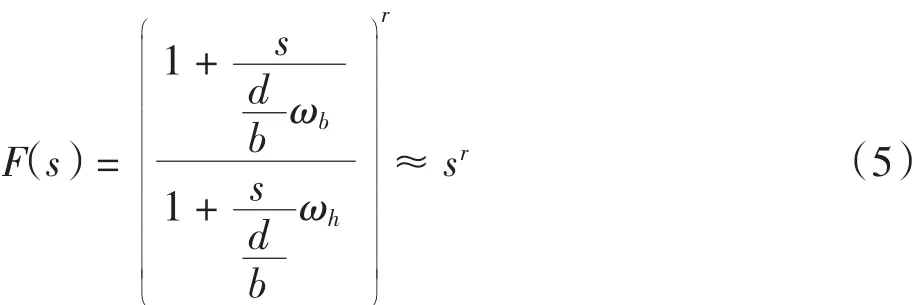
b、d分别为大于零的常数.将上式左侧变形得到：

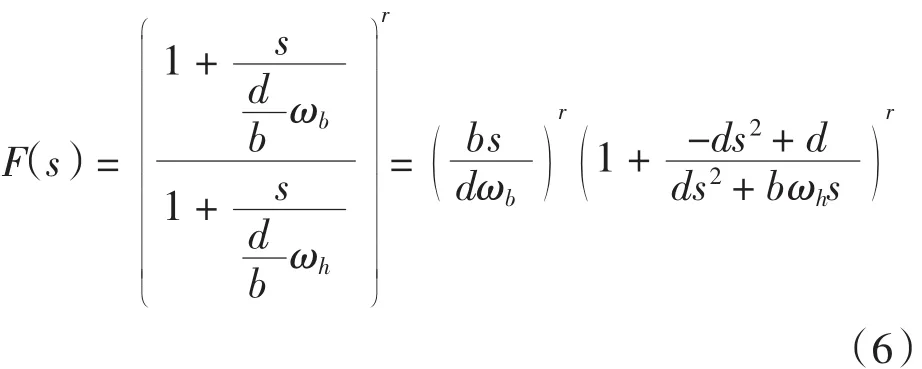
对上式右侧第二项进行二项式展开得到：

省略上式中展开式的二次项及更高项，得到：

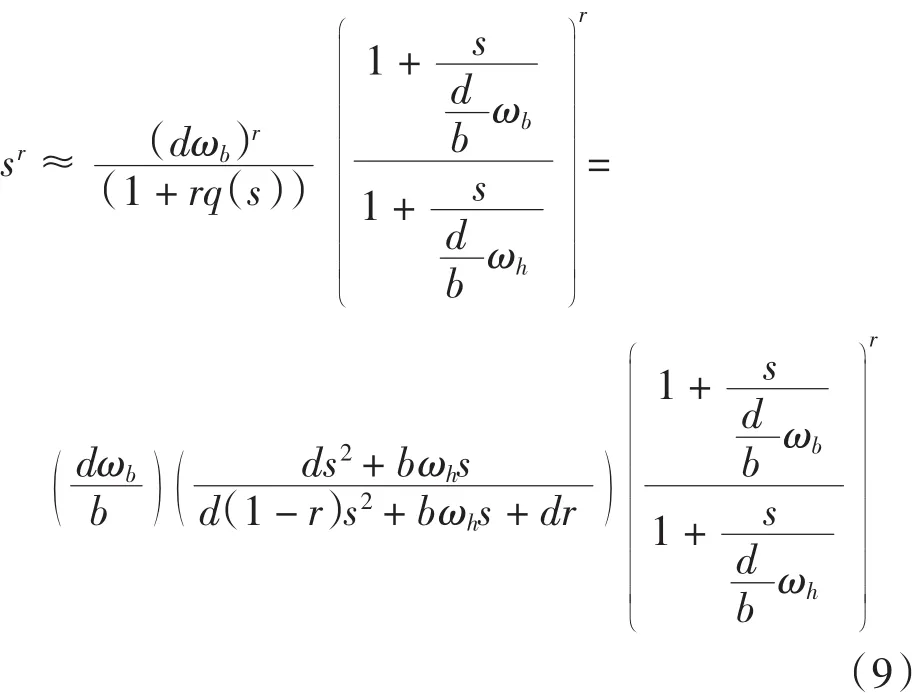
将s指数项化简式代入上式，得到分数阶算子逼近公式为：

对于上式中，s的指数项可以近似化简为：

根据经验公式，取b=10，d=9，ω′k和ωk分别取如下值：

1.2内模控制

内模控制[9]作为一种新的控制策略，它是基于过程数学模型进行设计的，其原理类似于Smith预估器[10].相比于传统的控制器，如PID控制器，内模控制具有设计简单[11]、能够抑制系统中扰动及不确定性[12-13]、设计后系统闭环模型阶次较低等特点.在直线电机工作中，其所受到的外部扰动应该在电流环中进行抑制，以避免其作用到外环当中；同时在直线电机系统建模过程中，通常将其简化为一个二阶系统以便于设计控制器，但这同时不可避免地引入了模型不确定性.基于上述原因，在直线电机驱动系统中，电流环控制器将采用内模控制进行设计.

图1为典型的内模控制下的系统结构图.图1中：C（s）为内模控制器；G（s）为实际被控对象；M（s）为被控对象的内部模型；r、y、yf、u和d分别为系统的输入信号、输出信号、反馈信号、控制量和外部扰动信号.

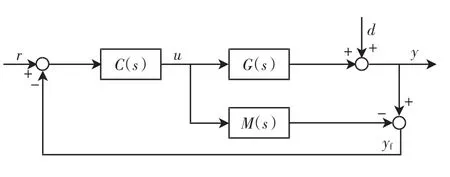
图1　内模控制结构Fig.1 IMC structure

通过对图1中的结构进行化简可以得到系统给的闭环响应及反馈信号分别为：

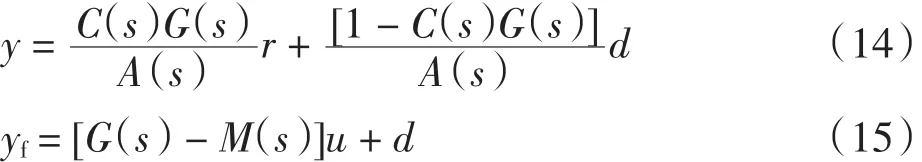
式中：A（s）= 1 + C（s）[G（s）- M（s）].从式（15）中可以发现，在模型精确、外部无扰动的情况下，反馈信号yf为零，此时系统变为开环形式.而在实际情况下，模型不确定性及外部扰动是一定存在的，这样反馈信号yf就对模型不确定性及外部扰动做出了反应，从而使系统具有闭环控制结构.

内模控制原理实际上就是一种状态观测器的思想，根据这一思想，内模控制系统的设计过程可以分为以下两个部分[14].

步骤1：过程模型分解

式中：M+（s）为模型中包含纯滞后和不稳定零点的部分；M-（s）为模型中的最小相位部分.

步骤2：内模控制器设计

内模控制器通过M-（s）的逆上增加滤波器，来实现系统给的稳定性和鲁棒性.给出内模控制器形式为：

式（4）中：f（s）是一个低通滤波器，引入f（s）是为了使得控制器时有理的，其通常被设计为：

式中：r为滤波器阶数，其应选择足够大以保证C（s）是正则的、物理上可实现的；α为滤波器的时间常数，它是整个控制系统中唯一的设计参数，使得控制器设计变得非常简单易于调试.

2　运动平台建模

根据直线电机动态特性[15]，若u为电机输入电压，R为等效总电阻，L为回路总电感，i为回路电流，e为反电势，m为负载质量，Ke为反电动势系数，Kt为推力系数，F为电机出力，则动态方程如下：

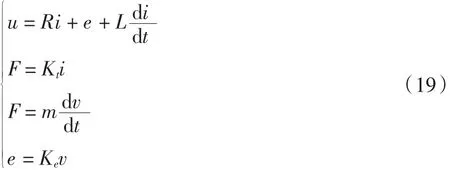
由于在实际过程中，电机采用专用驱动器，该驱动器采用SVPWM控制方式，即id≡0的控制策略，故对电机模型简化处理后对上式进行拉普拉斯变换，得出其简化模型传递函数为：

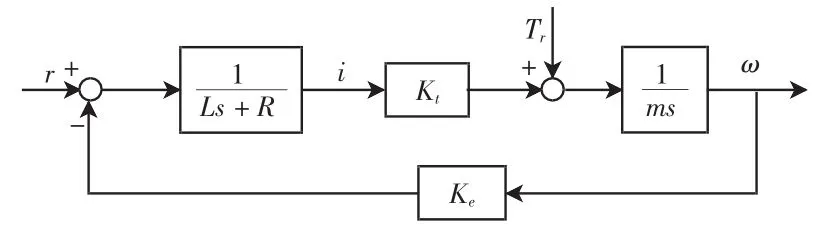
图2　直线电机简化模型Fig.2 Linear motor simplified model

3　控制系统设计

为了验证所提出控制策略的有效性，本文以光刻机掩模台宏动台作为被控对象，对其控制系统进行设计.在设计之前首先给出掩模台宏动台所用直线电机的参数，如表1所示.

表1　直线电机参数Tab.1 Parameters of linear motor

同时，宏动系统的总质量mz= 40 kg，由于宏动台由4个电机共同驱动，故单电机负载质量m = 10 kg.

3.1电流环设计

由于内模控制具有结构直观、参数整定容易和在线调整方便等优点，本文采用内模原理对系统电流环控制器进行设计.结合第2节建立的直线电机模型与第1节介绍的内模控制设计方法，可以得到系统电流环过程模型和控制器模型分别为：

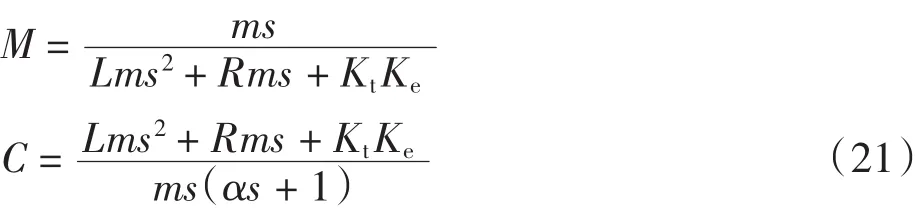
进一步可得到系统电流环闭环等效模型为Gt=.作为一个惯性环节，电流环模型相比于传统的PID控制器所构成的电流环模型更加简单，利于后面对速度环、位置环的设计.

为了保证电流环在快速性、抑扰性方面的性能，根据经验系统的电流环带宽通常设计在1 000 Hz左右.由电流环闭环等效模型，可以得到其带宽近似为1/（2απ），从而可以计算出控制器中时间常数近似为0.000 16.电流环闭环伯德图如图3所示.

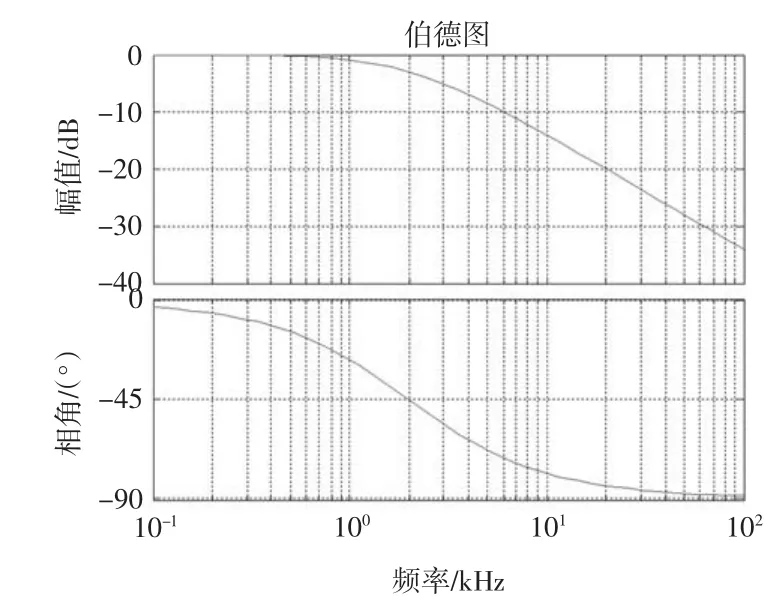
图3　电流环伯德图Fig.3 Bode diagram of current-loop

3.2速度环设计

通过对电流环的设计，可以近似得到速度环的开环被控对象模型为：

这表明了系统速度环被控对象是一个I型系统模型.为了获得高增益的同时避免带宽过高，选择PI控制器作为速度环控制器；并且由于电流环带宽远高于速度环，因此1/（αs + 1）部分的转折频率点远大于速度环剪切频率.因此，速度环开环系统将变为典型的II型系统：

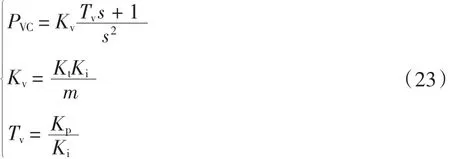
式中：PVC为速度环开环模型；Kp、Ki分别为PI控制器的比例增益系数及积分增益系数.速度环开环系统幅频特性示意图如图4所示.

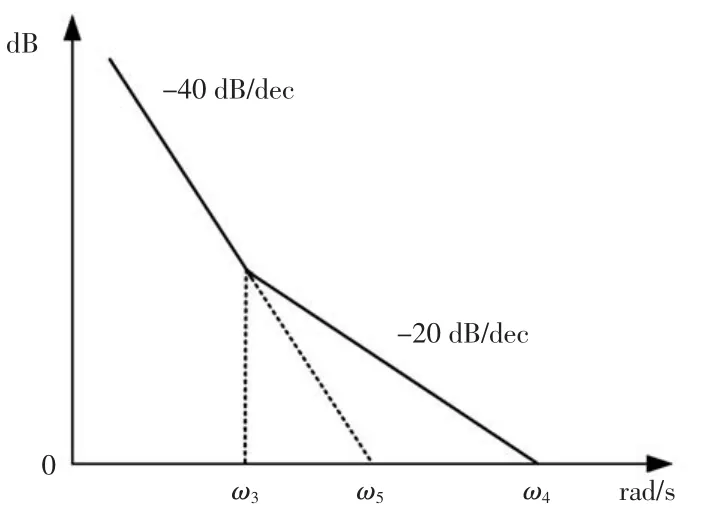
图4　速度环幅频特性示意图Fig.4 Amplitude-frequency characteristic diagram of velocity-loop

图4中：ω3为系统转折频率；ω5为-40 dB斜率线与零分贝线相交频率；ω4为系统剪切频率，其关系如式（24）所示：

在II型系统设计中，为了综合稳定性以及系统的等效噪声带宽，无量纲增益ω4/ω3常被设为2.根据式（24）、（25）可以得到要求：ω3≥573.57 rad/s.这里选定ω3= 600 rad/s，同时通过对（23）式、（24）式求解推导出式（26）：

为了跟踪所给出的正弦信号0.002 sin（10仔t）并使其跟踪误差不超过3滋m，速度环输入信号可以设计为0.02仔cos（10仔t），其跟踪误差不超过（30仔滋m/s）.并且由于速度环开环模型是一个II型系统，其跟踪误差可以近似为：

将各项参数代入（26）可以得到Kp= 129.1，Ki= 77 419.4.通过仿真可以得到速度环开环频率特性，如图5所示.

由图5可见，系统剪切频率约为206 Hz、相角裕度53.4°，满足设计要求.

跟踪信号0.02仔cos（10仔t）的稳态跟踪误差如图6所示.

通过仿真结果可以得到，所设计的控制器满足设计要求，其响应时间为4.2 ms，稳态误差不超过±86.2 滋m/s的误差带.

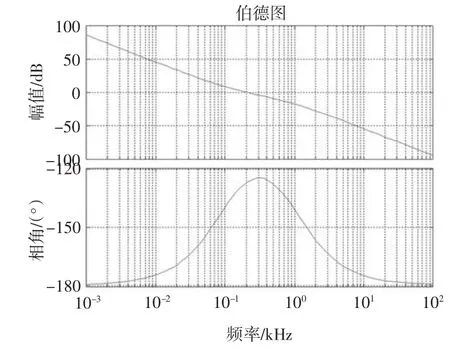
图5　速度环开环频率特性Fig.5 Open-loop frequency characteristic of velocity-loop

图6　速度环稳态跟踪误差Fig.6 Steady-state tracking error of velocity-loop

3.3位置环设计

为了提高系统控制精度、减小跟踪误差，在外环控制器上选择分数阶PID作为位置环控制器.分数阶PID相比于传统PID控制器，其增加了2个阶次参数使得控制器性能得以进一步提升，同时提高了系统的稳定裕度.

由上一节中所设计的速度环，可以得到位置环被控对象模型为：

通过之前的设计可得，分母上的三阶环节的转折频率远高于位置环工作频率，所以这个环节可以忽略.这里采用分数阶PI控制器对位置环进行控制，得到位置环的开环模型为：

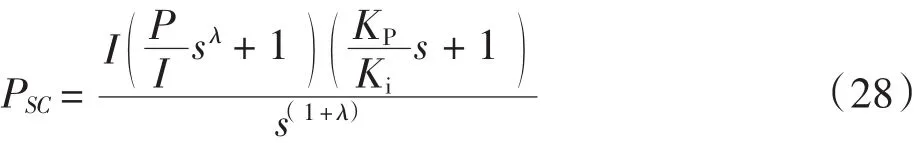
式中：P为分数阶PI控制器的比例参数；I为分数阶PI控制器的积分参数；姿为分数阶PI控制器的积分阶次参数.通过式（11）的近似以及对其中相应控制参数的调试，得到一组较为合适的参数：r=-0.5，N=4，[ωl，ωh] = [0.000，110 000（Hz），b = 10，d = 9，P = 1 000，I = 15.通过Simulink仿真得到系统跟踪信号0.002sin（10 πt）的位置跟踪误差曲线及稳态误差曲线分别如图7和图8所示.其中所提出的三环控制策略还与一组调试出来的效果较好的传统三环PID控制策略进行了对比，结果如图7所示.

图7　位置环跟踪误差Fig.7 Positioning tracking error

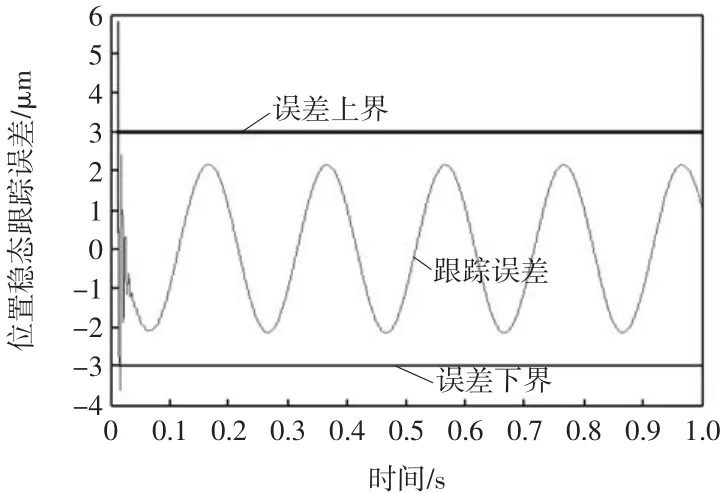
图8　分数阶PID方法位置环稳态跟踪误差Fig.8 Steady-state positioning tracking error by fractional order PID

由仿真结果可以得到，宏动系统位置跟踪稳态误差不超过±2.15滋m、调节时间为15 ms，而传统三环PID控制策略跟踪误差在±20滋m左右，相比于传统的三环PID控制策略，本文中所提出的控制策略跟踪精度显著提高，能够满足对于光刻机掩模台宏动系统的设计要求.

4　结语

本文针对长行程直线电机控制系统提出以内模控制作为电流环控制器、分数阶PID作为位置环控制器的控制策略.在实际电机系统调试中，三环PID控制策略是工程人员最为常用的控制算法.但由于在光刻机等超精密系统上安装了较多极易损坏且价格昂贵的精密光学设备，如：激光干涉仪镜组等，故使其速度环及电流环参数调试受到诸多限制.而本文所提出

的以内模控制作为电流环控制器的方法，相比于传统的三环PID控制策略，有效地降低了控制对象的阶次，使得控制器设计变得更加简便，各环参数更易于在工程实践中进行调节.在长行程直线电机控制系统的最外环——位置环的设计中，本文采用分数阶PID作为位置环控制算法，增加了2个可调的阶次参数，弥补了电流环内模控制器可调参数少、系统灵活性低的缺点，可以有效提高控制系统的定位精度.在本文的第4节中，以光刻机掩模台宏动系统为例，应用文中所提出的内模控制作为电流环控制器、分数阶PID为位置环控制器的控制策略进行了设计，并且对其进行仿真.通过仿真验证可以发现，相比于传统的三环PID控制策略，本文所提出的控制策略其设计方法、调试过程更为简单，并且跟踪精度得到了显著提升.

参考文献：

[1] OTTEN G，DE VRIES T J A，VAN AMERONGEN J. Linear motor motion control using a learning feedforward controller[J]. Mechatronics IEEE/ASME Transactions on，1997，2（3）：179-187.

[2] LEE J J，YOON H S，CHANG S K. A new cogging-free permanent-magnet linear motor [J]. Magnetics IEEE Transactions on，2008，44（7）：1785-1790.

[3] LEE T H，TAN K K，LIM S Y，et al. Iterative learning control of permanent magnet linear motor with relay automatic tuning [J]. Mechatronics，2000，10（1）：169-190.

[4] PODLUBNY I. Fractional differential equations[M]. San Diego：Academic Press，1999.

[5] PODLUBNY I. Fractional-order systems and PIλDμ-controllers [J]. IEEE Trans on Automatic Control，1999，44（1）：208-214. [6] PODLUBNY I. Fractional-order systems and fractional-order controllers[R]. Kosice：Slovak Academy of Sciences，2003.

[7] LUO Y，CHEN Y Q，AHN H S，et al. Fractional order robust control for cogging effect compensation in PMSM position servo systems：Stability analysis and experiments[J]. Control Engineering Practice，2010，18（9）：1022-1036.

[8]王伟峰.复合驱动光刻机掩模台的运动控制研究[D].哈尔滨：哈尔滨工业大学，2014. WANG W F. Research on motion control for compound driven reticle stage of lithography[D]. Harbin：Harbin Institute of Technology，2014.

[9] GARCIA C E，MORARI M. Internal model control：A unifying review and some new results [J]. Ind Eng Chem Process Des Dev，1982，21（2）：308-323.

[10] ZHAO Z C，LIU Z Y，ZHANG J G. Robust IMC-PID controller design for an opto-electronic tracking system with timedelay[J]. Opto Electronic Engineering，2010，37（1）：30-36.

[11] RIVERA D E，MORARI M，SKOGESTAD S. Internal model control：PID controller design[J]. Industrial & Engineering Chemistry Process Design & Development，1986，25（1）：252-265. [12] LANDAU I D，CONSTANTINESCU A，REY D. Adaptive narrow band disturbance rejection applied to an active suspension：An internal model principle approach[J]. Automatica，2005，41（4）：563-574.

[13] WEN T，MARQUEZ H J，CHEN T. IMC design for unstable processes with time delays [J]. Journal of Process Control，2003，13（3）：203-213.

[14]赵志诚，文新宇.内模控制及其应用[M].北京：电子工业出版社，2012：1-7. ZHAO Z C，WEN X Y. Internal Model Control and Its Application[M]. Beijin：Electronic Industry Press，2012：1-7.

[15]杨天博.铁芯式直线电机定位力扰动的模型辨识与补偿方法[D].哈尔滨：哈尔滨工业大学，2014. YANG T B. Research on model identification and compensation for cogging force of iron-core linear motor [D]. Harbin：Harbin Institute of Technology，2014.

Control system design of long-stroke linear motor based on fractional order PID and internal model control

CHEN Xing-lin，CHEN Zhen-yu
（Department of Control Science and Engineering，Harbin Institute of Technology，Harbin 150001，China）

Abstract：In order to achieve the precision control of the long-stroke linear motor，a control strategy combining the fractional order PID control and internal model control is proposed. The internal model controller and the fractional order controller are used for current loop and position loop respectively. This strategy can make the control of the longstroke stage system accurately，simplify the design of controller and reduce difficulty of debugging，ensuring the tracking precision at the same time. Finally，a simulation on the long-stroke stage system of lithography machine is made and the proposed method is proved to be effective.

Key words：fractional order PID control；internal model control；control system design；linear motor；lithography machine

通信作者：陈兴林（1963—），男，教授，主要研究方向为飞行器控制及仿真精密数字控制. E-mail：chenxl@hit.edu.cn

基金项目：国家科技重大专项基金资助项目（2009ZX02207）

收稿日期：2015-10-21

DOI：10.3969/j.issn.1671-024x.2016.01.012

中图分类号：TP391

文献标志码：A

文章编号：1671－024X（2016）01－0059－06