基于高中数学三角函数教学要点的思考

韦莉

摘 要：高中数学课堂教学的实效性是一线教师关注的重点话题，三角函数是高中数学的重点内容之一，每年高考必考内容之一，本文从四个方面阐述突破三角函数重点和难点教学的具体方法与措施，以飨读者.

关键词：高中数学；三角函数；重点与难点

三角函数是高中数学教学的重点和难点，不仅有许多概念和公式需要学生理解与记忆，如诱导公式和基本关系式等，而且数学思想和解题方法较多，如类比思想、数形结合思想和分类讨论思想等，使得学生在学习中感觉力不从心. 因此，在高中数学三角函数教学中，教师需要把握教学的要点，帮助学生构建完整的知识体系，提高学生的分析能力和解题能力.

巧妙利用口诀，帮助学生记忆三角函数公式

在高中数学三角函数中，学生需要记忆很多公式，如果单纯采用死记硬背的方式，不仅记忆效果较差，而且不利于学生理解和应用，所以高中数学教师可以巧妙利用口诀，帮助学生记忆三角函数公式，使教学效果事半功倍.

在判断三角函数在不同象限的符号时，教师可以利用口诀“一全二正三切四余”帮助学生记忆，其含义为：第一象限，正弦函数、余弦函数和正切函数的符号均为正；第二象限，只有正弦函数符号为正；第三象限，只有正切函数符号为正；第四象限，只有余弦函数符号为正，这样学生很容易就可以依据角所在象限判断其三角函数符号. 在三角函数诱导公式的记忆中，教师可以让学生将角2kπ±θ、kπ±θ、±θ、±θ和±θ等形式均写成n×±θ的形式，然后根据公式特点，将诱导公式概括为“奇变偶不变，符号看象限，把θ看成锐角”，其中“奇变偶不变”的含义为：当n为奇数时，函数名称改变，即正弦函数与余弦函数的名称互换；当n为偶数时，函数名称不变.“符号看象限，把θ看成锐角”的含义为：在实际题目中，无论角θ的度数大小，只需要将其“看成”锐角，然后根据角±θ所在象限判断函数符号.

教师利用口诀帮助学生记忆诱导公式，既不会增加学生的学习负担，又可以帮助其很快找到解题思路和方法，使学生轻松解决三角函数中的化简求值难题.

灵活借助图象，帮助学生记忆三角函数性质

三角函数是特殊函数，既有一般函数的性质，如定义域、值域、奇偶性和单调性，又有其特有性质，如对称性和周期性，涉及的知识点比较多，如果学生单纯依靠记忆背诵，很容易出现记错和记混的情况. 因此，教师可灵活借助图象，帮助学生记忆三角函数性质.

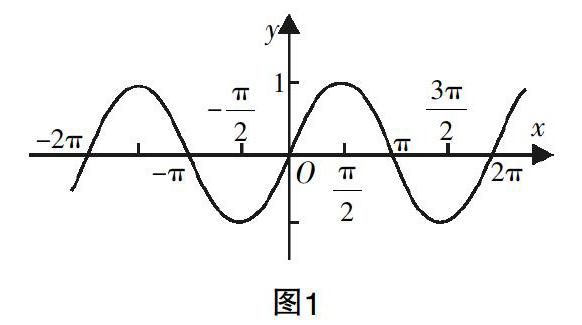
例如：学生记忆正弦函数性质时，教师可以借助正弦函数图象（如图1所示），帮助学生逐一讲解正弦函数性质，加深学生对正弦函数性质的理解.

正弦函数图象直观清晰，学生可以顺利总结归纳出正弦函数的各种性质，同样的方法可以应用于余弦函数和正切函数中，这样既有利于学生记忆和掌握三角函数性质，又可以让学生对正弦函数、余弦函数和正切函数的性质进行比较，构建完整的知识体系.

丰富教学手段，攻克三角函数变换的重难点

在三角函数中，传统教学模式主要为教师利用黑板和粉笔，进行理论知识的讲解，其教学过程枯燥单调，无法激起学生的学习热情. 因此，教师需要丰富教学手段，如利用多媒体进行教学，增加课堂教学的趣味性和生动性，让学生积极参与到教学过程中，从而提高课堂教学的质量和效率.

例如：在讲解y=Asin（ωx+θ）中振幅变换、周期变换和相位变换时，如果采取手绘图形讲解的方式，不仅耽误课堂教学时间，而且教学效果也难以尽如人意. 教师可以利用多媒体技术，将三角函数图形变换情况展示出来，这样既生动形象，又便于观察，可以有效帮助学生攻克三角函数变换的重难点.

最后，教师借助相位变换、周期变换和振幅变换，总结归纳出函数y=sinx→y=Asin（ωx+θ）的变换规律：相位变换是图象上的点向左或者向右平移θ个单位；周期变换是图象上的点横坐标变为原来的倍；振幅变换是图象上的点纵坐标变为原来的A倍.

注重一题多解，提高学生三角函数解题能力

在三角函数教学中，很多学生虽然记住了公式口诀，掌握了数形结合的思想，但是在实际应用时不能迅速找到正确的解题方法，无法真正做到学以致用.因此，教师需要有意识地让学生进行一题多解，提高学生三角函数的解题能力，避免学生陷入题海战术中.

从两种解题方法可以看出，解法一相对简单，而解法二较为烦琐，学生在求解相似题目时，可以选择解法一，以便提高解题速度. 一题多解可以有效拓宽学生的解题思路，使学生在面对三角函数题目时，可以快速找到正确的解题思路和方法，提高解题的准确性.

总之，在三角函数教学中，教师需要把握教学要点，如诱导公式、三角函数性质、图形变换和解题方法等，利用公式口诀、图象、多媒体技术和一题多解等教学方法及手段，加深学生对教学要点的理解与掌握，真正实现教学相长的目的.