面向麦弗逊悬架性能开发的柔性减振器建模及应用

陈广彦　孙晖云　赵永坡　方超　李朋

（长城汽车股份有限公司技术中心河北省汽车工程技术研究中心，保定071000）



面向麦弗逊悬架性能开发的柔性减振器建模及应用

陈广彦孙晖云赵永坡方超李朋

（长城汽车股份有限公司技术中心河北省汽车工程技术研究中心，保定071000）

【摘要】为解决乘用车常用的麦弗逊悬架在开发过程中出现的性能指标计算精度差、底盘调校效率低等问题，分析了麦弗逊悬架减振器侧向力成因及对车辆性能的影响。采用虚拟衬套法构建了柔性减振器模型，并在几款车型上进行动力学性能开发验证，结果表明该方法提升了麦弗逊悬架及整车性能的预测精度，有利于前期的性能设计和后期的底盘调校。总结了柔性减振器建模及在车型应用中的经验。

1　前言

麦弗逊悬架由减振器总成、下摆臂以及转向节总成构成，其由于结构部件少而具有质量小和价格低的优势，被广泛用于乘用车的前桥上。但这种悬架的减振器会受到比较明显的侧向力，该力是麦弗逊悬架摩擦力的主要来源之一[1]。景立新等针对麦弗逊悬架建立柔性弹簧模型并对减振器侧向力进行了优化[2]；柳江等采用有限元法对侧载弹簧进行了优化设计[3]。减振器侧向力会影响悬架性能尤其是侧向性能，最终会对整车不足转向度等指标产生影响。

在动力学性能分析中，减振器大都采用约束法进行建模，但在麦弗逊悬架性能分析中遇到了精度低的问题，对前期性能设计及后期底盘调校产生了不利影响。为解决精度低的问题，一些研究机构对约束法进行了改进，如：景立新等采用辅助刚体法描述减振器受力[2]。对减振器阻尼力进行建模的文献较多，但对减振器侧向力建模的文献较少。本文对减振器侧向力的形成机理进行了分析，以此为基础构建了侧向力计算模型应用于车型开发中，并证明这种模型能够提升麦弗逊悬架性能的预测精度。

2　减振器侧向力分析

在麦弗逊悬架中，减振器总成的下端（活塞筒）与转向节之间通过螺栓固连到一起，上端通过衬套与车身相连，活塞筒与转向节固连。可以将车轮、转向节及减振器看成一个整体进行受力分析，如图1所示。

对导向铰点G求矩可得：式中，FYE为车身连接衬套处的侧向力；FZ为轮胎垂向力；a为活塞筒上端到车身连接点的距离；b为活塞筒长度；c为FZ对导向铰G的力臂；E为减振器与车身的固定点。

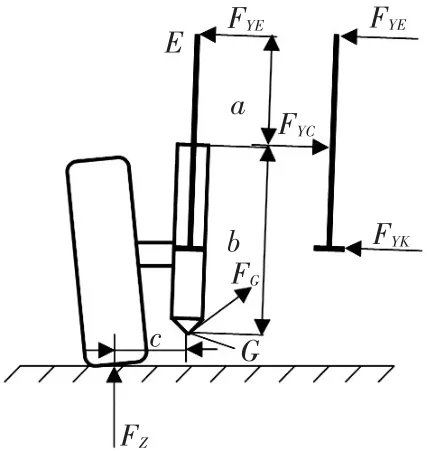
图1　麦弗逊悬架减振器受力分析

由于轮胎垂向力FZ绕导向铰G的力臂c而产生了车身连接衬套处的侧向力FYE，这个力会引起衬套变形，而由于FYE的作用，在活塞杆导向套和活塞阀上产生了侧向作用力FYC和FYK，所以有FYC=FYE+FYK。这个力越大，作用在活塞杆导向套上的摩擦力就越大，这样就会增加车辆在低速行驶时和平整道路上行驶时的振动加速度，对平顺性产生负面影响；减振器侧向力对轮胎侧向力产生一定贡献，最终使轮胎侧偏角发生改变，所以这种力也会影响车辆的操纵稳定性。

在车辆行驶过程中，悬架会产生跳动，这两处的侧向力有时变的特性，如图2所示。对于活塞筒而言，导向套处的受力，区域是不变的，而对于活塞杆而言，受力区域会随悬架跳动而不断改变；活塞阀处的受力是活塞阀与活塞筒壁之间的作用力，同理，此处活塞阀受力区域是不变的，而活塞筒壁受力区域会随悬架跳动而不断改变。

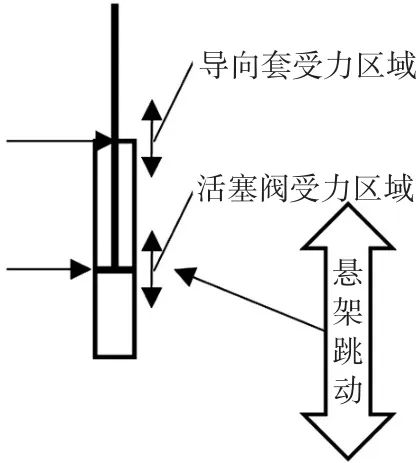
图2　减振器侧向力区域的时变性

3　约束算法及其使用效果

减振器由活塞杆、活塞筒组成，活塞杆可以相对于活塞筒转动和滑动。常规建模方法采用圆柱副描述这种运动关系，活塞杆、活塞筒为刚体。为了检验模型的精度，将仿真结果与K&C试验结果进行对比，对悬架侧向力转向特性进行考察，选择前悬架为麦弗逊型式的车型进行研究，4款车型的使用效果如图3所示。

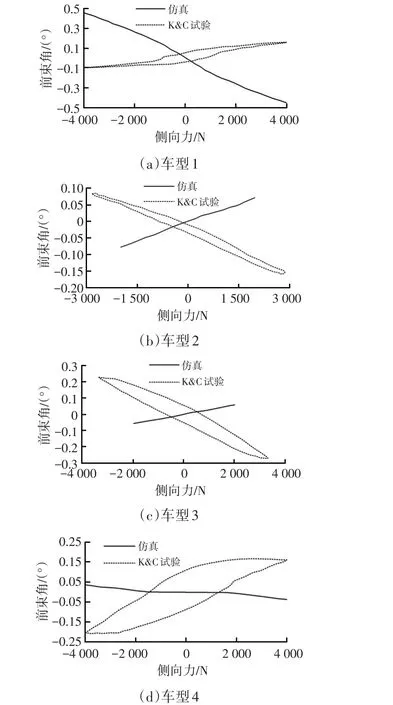
图3　侧向力转向特性对比

由以上结果可知：使用约束法的减振器模型，侧向力转向特性的计算精度很差，与试验结果的趋势刚好相反，且其他转向特性（如回正力矩等）也出现了趋势相反的情况，如此就无法准确设计悬架的K&C特性。

圆柱副约束了活塞筒与活塞杆2个点之间的运动行为，约束反力也是作用到2个点上，而且作用点相对于刚体的位置不发生改变，但实际上减振器有2个受力区域（活塞阀处和活塞筒口的导向套处），这2个区域随着轮跳而发生变化。由此可见，约束法无法准确描述减振器的侧向受力，最终导致K&C计算结果与试验结果偏差过大。

4　柔性减振器的建模原理

为了解决约束法带来的问题，按照减振器的受力特性进行建模。在跳动过程中，减振器的受力区域不断变化，为了描述这种时变效应，考虑活塞杆、活塞筒的变形，在多体分析中将其作为柔性体处理，这需要在有限元分析软件MSC.NASTRAN中计算CB模态[4]。

活塞杆与活塞筒之间的作用力为接触力。目前的多体分析软件大都支持建立柔性体之间的接触，但是受数值求解能力的影响[11]，计算速度慢且精度较低，且由于车辆动力学性能开发中包含多种工况的计算，使得这种方法严重影响了车辆性能计算效率和质量。为了解决这些问题，必须对接触力进行简化。接触问题中主要包括接触刚度和接触阻尼2种属性[5]。活塞杆与活塞筒之间的侧向力属于接触力中的法向力，忽略接触过程中的刚度、阻尼变化以及接触搜索过程，可以用下面简化的式子描述：式中，Fn为法向力；Kn为接触刚度；Cn为接触阻尼；δn为接触区域的法向变形；vn为法向变形速度。

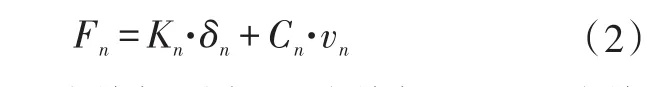
这种算法与橡胶衬套力的算法[6]很接近，不妨称之为“虚拟衬套力”，这种力在点与点之间进行定义，如此就节省了搜索时间，提高了计算效率。

减振器2个区域存在时变特性，这就需要定义一系列的衬套力，衬套力的范围按照减振器跳动行程设定。当构成力的2个点之间的距离小于某一数值时，这种衬套力不为0，当此距离大于某一数值时，力变为0。为了模拟这种时变效应，可以定义一个阶跃系数，阶跃系数s的计算方法如下：式中，a=h1-h0为阶跃系数的差值；Δ=(x-x0)/(x1-x0)为阶跃距离的差值；x0为初始阶跃距离；x1为最终阶跃距离；h0为初始阶跃距离所对应的系数；h1为最终阶跃距离所对应的系数。

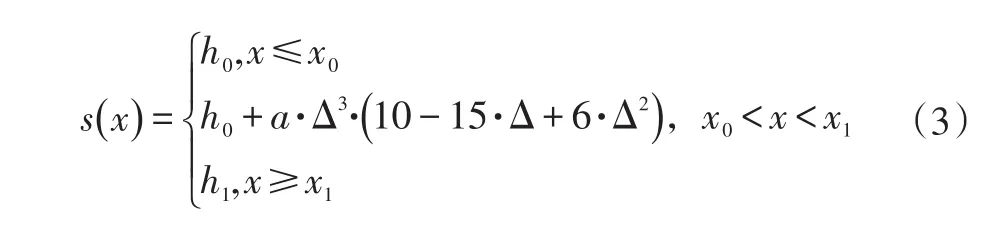
阶跃函数曲线见图4，它的1阶、2阶导数连续，3阶导数在h0和h1处连续，这样就有利于数值求解，侧向力按照公式（4）计算。

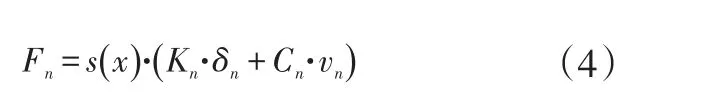
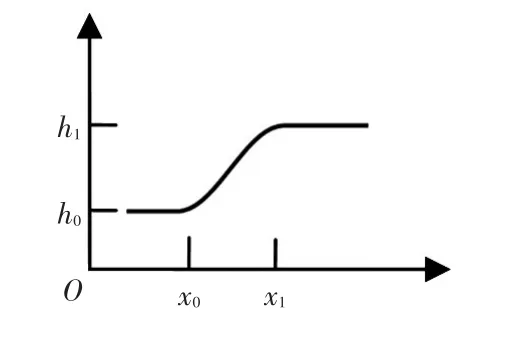
图4　阶跃函数

当受力点在垂向上的距离为0时，侧向力最大，阶跃系数设为1，0即为初始阶跃距离，当受力点的距离超过某一数值时，侧向力最小，阶跃系数设为0，所以x0=0，h0=0，x1=xc，h1=1，其中xc即为最终阶跃距离，它的数值可以参考活塞阀、油封（导向套区域）的高度，在减振器图纸上测量即可。

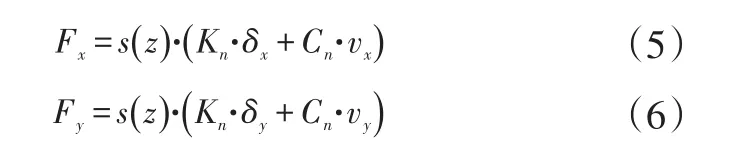
选取减振器的垂向为局部的Z向，上述侧向力Fn就可以分解到局部的X、Y向，见公式（5）、（6）。式中，s（z）为局部Z向的阶跃系数；δx、δy为局部X、Y向的的变形；vx、vy为局部X、Y向的变形速度。

以活塞阀受力为例，侧向力分布如图5所示。

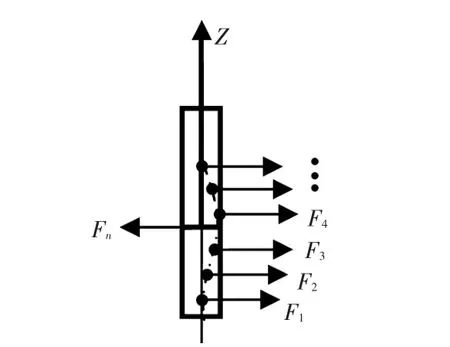
图5　活塞阀的侧向力分布

活塞筒及活塞杆的中心线上需要建立一系列多点约束，这些多点约束中的参考节点负责将受力分解到体单元或板壳单元的节点上。一般来说，活塞杆需要用体单元建模，而活塞筒需要用板壳单元建模。由于多点约束与力的分解有关，所以必须建立RBE3，RBE3不会增加结构的刚度，它的参考节点为从节点，从节点运动通过独立节点运动耦合完成。从节点为力和力矩的直接作用点，它按照加权方式将力和力矩分解到实际的体单元或板壳单元的节点上，计算过程参考图6和公式（7），一般单元上的节点只受到力。这里为注释方便，假设重心周围的4个节点为独立节点，实际数量不受限制。MSC.NASTRAN中采用静态凝聚法[7]计算局部模态，由于RBE3节点主从性与求解要求不符，在计算模态时需要转换参考节点的主从性。

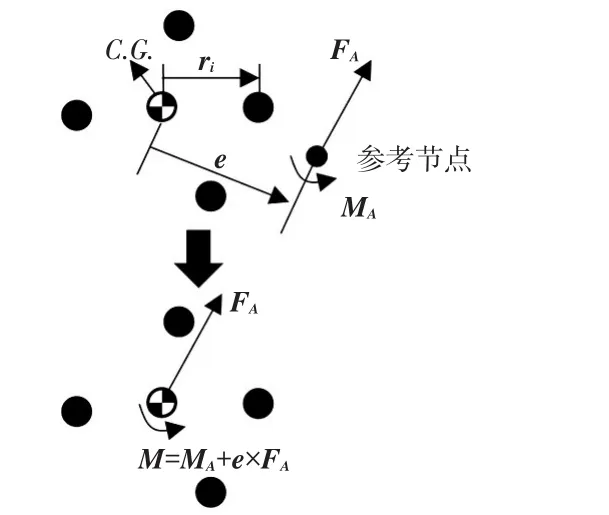
图6　RBE3受力分解

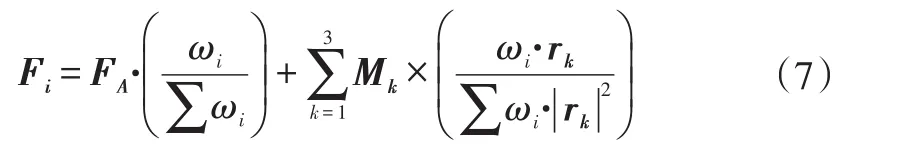
图6和式（7）中，C.G.为独立节点的加权重心（以下称重心），也就是所有独立节点的等效“中心位置”；e为参考节点与重心之间的位移向量；Fi为每个独立节点的受力；FA为参考节点所受的力；M为平移至重心之后的力矩；Mk为M在单个坐标轴上的分量；ωi为加权系数；ri为重心与每个独立节点之间的位移向量；rk为ri在单个坐标平面的分量。这里对力矩分解作出解释：共3个坐标轴X、Y、Z和3个坐标平面XOY、YOZ、ZOX，坐标平面为坐标轴的法平面，如X轴对应YOZ面。参考节点位于减振器的中心线上，相对于中心线的偏移量即为侧向变形δn，按照式（2）～式（7）将侧向力分解到了单元的节点上。

5　车型开发的验证和应用

车型1为一款SUV，在该车型上进行柔性减振器使用精度的验证，采用柔性减振器的前麦弗逊悬架模型如图7所示。

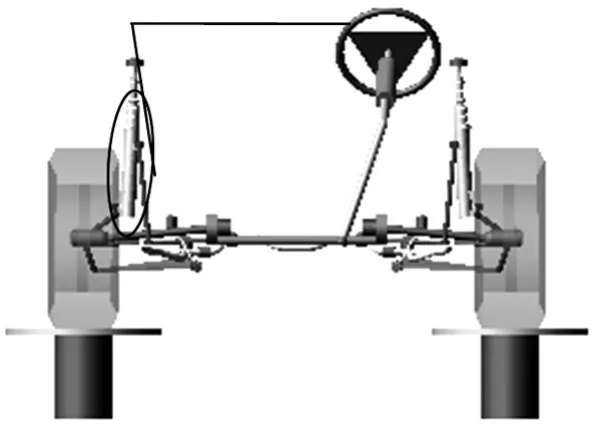
图7　某SUV车型的前麦弗逊悬架模型

使用英国ABD试验台进行K&C性能测试，如图8所示，测试的主要目的是验证K&C性能设计的合理性，同时希望找出性能改进点。

图8　某SUV车型的K&C性能测试示意

采用柔性减振器模型后，该车前悬架侧向力转向特性的对比如图9所示。

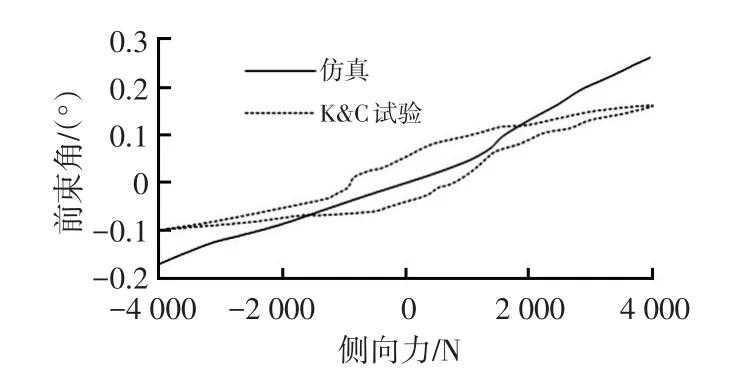
图9　某SUV车型前悬架侧向力转向特性曲线

可见，与常规减振器模型相比，采用柔性减振器的侧向力转向特性曲线与K&C试验曲线的趋势一致，同时可知车型2～车型4的侧向力转向特性曲线与试验曲线的趋势也是一致的。

为了对柔性减振器模型进行充分验证，将整车不足转向度的计算结果与客观试验结果进行对比：车型1的试验结果为0.19°/（m·s-2），常规减振器模型的计算结果为0.15°/（m·s-2），采用柔性减振器模型的计算结果为0.20°/（m·s-2），该指标的计算精度有所提升。车型2～车型4的不足转向度计算精度也均有提升。这说明在当前建模流程下，采用柔性减振器模型后，悬架性能和整车性能的计算精度都得到了一定的提升。

采用柔性减振器模型后，前期性能设计精度得到提升，底盘调校阶段也可以根据计算结果制定不同的悬架零部件匹配方案，提升效率。

采用柔性减振器模型是提升麦弗逊悬架性能分析精度的重要手段之一，但仅靠这种模型仍无法解决所有的精度问题。在悬架性能分析中，必须根据车型开发目标以及悬架结构找出影响计算精度的主次因素，找到合理的解决方案。

6　柔性减振器应用小结

a.对于整车操纵稳定性能设计和悬架K&C性能设计，减振器侧向力的贡献不可忽视，如果侧向力计算不准确，则无法得到准确的性能设计结果；

b.柔性减振器模型中存在阶跃系数，尽管该系数由3阶连续函数计算得来，但仍会影响侧向力的计算精度，为此需要结合试验改进阶跃系数的算法；

c.为了得到满足车辆性能要求的侧向力，在底盘调校阶段进行减振器侧向力测试是必要的。

参考文献

1 Mitsche M，Wallentowitz H.汽车动力学.北京：清华大学出版社，2009：321～324.

2景立新，郭孔辉，卢荡.麦弗逊悬架减震器侧向力优化.科学技术与工程，2011，11（1）：71～75.

3柳江，喻凡，楼乐明.麦弗逊悬架侧载螺旋弹簧优化设计.汽车工程，2006，28（8）：743～746.

4 Reymond M A. MSC.NASTRAN DMAP Programmer’s Guide. California：The MacNeal-Schwendler Corporation，2000：32～35.

5 Wriggers P,Laursen T A. Computational Contact Mechanics. Italy：SPIN，2007：134～135.

6周长城.车辆悬架设计及理论.北京：北京大学出版社，2011：186～192.

7张永昌.MSC.NASTRAN有限元分析理论基础与应用.北京：科学出版社，2004：257～259.

（责任编辑斛畔）

修改稿收到日期为2015年11月19日。

The Flexible Shock Absorber Modeling and Application for MacPherson Suspension Performance Development

Chen Guangyan, Sun Huiyun, Zhao Yongpo, Fang Chao, Li Peng
（R&D Center of Great Wall Motors Company, Automobile Engineering Technology Center of Hebei, Baoding 071000）

【Abstract】In order to solve the development problems of passenger car MacPherson suspension, i.e. poor accuracy of performance index calculation, low efficiency of chassis tuning, etc., the cause of shock absorber’s lateral force and its effects on vehicle performance are analyzed. The flexible shock absorber model is built through the method of virtual bushing. The model is verified in the dynamic performance development of several cars. The results show that the proposed method improves the performance prediction precision of Mcpherson suspension and vehicle. It’s conducive to performance design and chassis tuning. The experiences in flexible shock absorber modeling and application are summarized.

Key words:Mcpherson suspension, Lateral force, Virtual bushing, Flexible shock absorber, Dynamic performance

中图分类号:U463.33+5.1

文献标识码:A

文章编号:1000-3703（2016）02-0011-04

主题词:麦弗逊悬架侧向力虚拟衬套柔性减振器动力学性能