巧借数学反例,提高学生思维品质
2016-03-17江苏省苏州市吴江区松陵高级中学
江苏省苏州市吴江区松陵高级中学 唐 健
巧借数学反例,提高学生思维品质
江苏省苏州市吴江区松陵高级中学 唐 健
本文从引入反例,强化数学概念的认识与应用;巧借反例,在复习巩固中温故知新;运用反例,帮助学生快速判定命题的正确与否;借助反例,培养学生数学发散思维能力四方面出发,探讨了在高中数学教学中对反例教学的开展策略,以期能引导学生从反面去思考、解决问题,从而培养学生的逆向思维能力,提高学习效率。
高中数学 反例教学 数学思维
波利亚说:“类比和反例是获得发明的伟大源泉。”在数学发展史上,反例和证明同等重要。在高中数学中,若能充分利用反例,则会发现数学的世界原来别有洞天。利用反例论证不但运算量小,而且具有说服力强的优势,引导学生换个角度去思考和解决问题,培养学生的逆向思维能力,发展学生的数学思维。下面,笔者就结合具体的教学实例,从如下四方面对高中数学教学中反例教学的开展策略略谈浅见,以供同行参考。
一、引入反例,强化数学概念的认识与应用
精练的数学概念无疑浓缩着数学思想与方法的精华,不管是培养学生良好数学思维品质,还是发展学生的数学思维,都离不开对数学概念的认识与应用。但在教学中,如果教师将这些抽象的概念、定义、法则等强制灌输给学生,那么,失去了理解的基础,死记硬背的方式只能是短时间的记忆,更别谈将知识内化了。运用反例教学,可以加深学生对数学概念的理解,避免理解上的混淆,更好地强化对数学概念的认识与应用。
例如正切函数的一个重要性质:“在每一个区间上是增函数”,由于正切函数的定义域也是Z),因此有部分学生认为:“正切函数在整个定义域内是增函数”这个命题是正确的。为此,我们不妨引入反例,如果要想检验一句话正确与否,我们可以列举出一个满足该命题条件的反面例子来证明这句话是错误的。如图所示,x取0,与x取π时,函数的值是相等的。第一个周期里的 tan45°与另外一个周期里的tan225°是相等的,这样说明“正切函数在整个定义域内是增函数”这个命题就是错的。正切函数的单调性只能在某一个周期内讨论,在(-π/2+kπ,π/2+kπ)(k∈Z)上是单调的,但是在整个定义域R上不具有单调性。
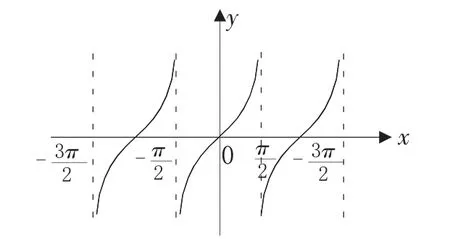
可见,在数学概念、定理、法则的运用过程中,通过运用反例,可以避免繁琐、抽象的推理论证过程,不仅大大节省了做题时间,也能给学生留下较为深刻的印象。
二、巧借反例,在复习巩固中温故知新
对命题的真假,学生往往习惯了从正面去证明,有时需要耗费大量的时间和精力去给予严密的证明,而面对假命题时,运用反例则能做到迅速鉴别,这是更正错误、否定谬误结论的有效武器。课堂时间毕竟有限,而高中数学知识面广泛,课堂安排紧密,运用反例教学则可以大大提高解题速度,又能帮助学生在反例的列举中达到温故而知新的效果。
例如有一道判断题:“方程的解即为方程的根”,很多同学都认为这句话是对的,根就是解。为了让学生认识到解与根是有区别的,我列举学生在初中时学过的一元一次方程和高中才学的多元方程,对于一元一次方程来说,解与根没有区别,方程的根也叫方程的解。而对于多元方程来说,方程的解就不能说成是方程的根,这时解与根是有区别的,根可以不成立,但解不可以。
可见,一些经典的反例教学题的运用能有效巩固学生所学的数学新知识,提高了学生对知识的全面理解度。引导学生构建反例,往往能使学生在认识上产生质的飞跃,提高学生思维的缜密性。
三、运用反例,帮助学生快速判定命题的正确与否
判断一个命题是否成立,一般的做法往往是直接从正面去证明。但有时候,如果直接从正面证明的话费时费力,还容易出错,尤其是在证明这个命题为假命题时,如果通过反例来证明,反而更快速,也更容易让学生接受,大大提高学生的解题速度。
例如,判断命题“无理数的无理数次幂仍为无理数”是否成立。
对于这道判断题,如果从正面去证明,短时间内是很难讲得明白的。但如果让学生以“挑毛病”的形式去举出一个具体的反例来,反而更具说明力。在这个命题中,以无理数为例,如果是无理数,那么(等于2是有理数,这不就是一个最好的反例证明吗?
再比如:判断“子集是由原来集合中的部分元素所组成的集合”这句话是否正确。有些同学容易把全集理解为“全体”,子集理解为“部分”,误认为此命题正确。但如果运用反例,我们只要举例空集,空集是任意集合的子集,但空集中并不含有命题中所说的“部分元素”,一下子就能判断命题是假命题。
可见,反例是否定谬论最直接的武器。学生列举反例的过程,也正是学生巩固所学内容,提高数学能力的过程。
四、借助反例,培养学生数学发散思维能力
发散思维又称求异思维,其思维特点是具有逆向性、侧向性和多向性,现为思维视野广阔。在教学中,培养学生的发散思维有利于学生多方向、多角度地去思考、分析和解决问题。而反例教学,需要学生分清条件的充分性与必要性,且造反例带有一定的技巧性,正是培养学生发散思维的一种很好的教学方式。
例如:已知f(x)是定义在R上的函数,且对于任意的a,b∈R都满足f(ab)=af(b)+bf(a),请问f(x)是否一定为常数函数?为什么?
对于此题,我们很容易想到f(x)=0是满足题意的一个函数,但如果认为f(x)一定是常数函数,我们发现证明很困难。于是我们就尝试从另一个角度来思考,即f(x)不一定必须是常数函数。为了支撑这个观点,那就必须找出能够证明这一观点存在的反例。通过观察本题中给出的式子构造,f(ab)=af(b)+bf(a),具有一定的对称性,所以我们可以尝试对本式进行变形处理。当ab≠0时,我们可以令式子两端分别除以ab,得到如下结果:我们取那么上式变为F(ab)=F(a)+F(b),这个式子恰恰就是我们学过的对数函数的模型,显然对数函数不是常数函数,我们找到了反例,从而得出结论,f(x)不是一定为常数函数。
我们还需要将F(x)的具体形式构造出来,并代入题意验证。取F(x)=logax(a>0,a≠1),从形式上看,F(x)满足题目中的条件,但是题目中的定义域是x∈R,目前我们的F(x)的定义域是x>0,我们需要作出一些改变,取1),此时,我们还有一种情况没有考虑到,即x=0时,结合题目条件,我们可以令x=0时,f(x)=0,此时我们得到:

上述f(x)就是符合题目条件的反例,事实上,我们可以发现只要满足下面式子的f(x)都是符合题目条件的反例。
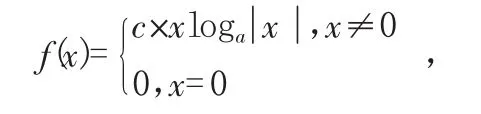
c是任意非零常数。
可见,在上述案例中,不局限于既定的理解,能够换个思考的角度去探索和解决问题,思维上的变通和开放反而让我们的解题思路别有洞天!
综上所述,反例是帮助学生强化数学概念、掌握定理、公式、提高数学思维能力的有效武器。我们教师不能简单地视“反例”仅仅为“反例”,而忽视了反例在数学中应有的积极作用,只要我们能根据教学内容的需要,引入恰当的反例,换一个角度往往别有洞天!抛砖引玉,希望大家能从这篇小文章中有所收获。
[1]林美娟.注重反例教学,培养学生的发散思维能力[J].科技信息.2008.31
[2]黄艳玲.主动发挥反例的作用[J].中小学数学.2009.7
[3]冯凌.反例在高中数学概念教学中的作用[J].中学数学研究.2014.21
[4]杨昌海.反例在数学教学中的运用[J].考试周刊.2012.17
