把握规律,促进思维
——教学“乘法分配律”后的思考
2016-03-17浙江省杭州市萧山区党湾二小萧百奇
浙江省杭州市萧山区党湾二小 萧百奇
把握规律,促进思维
——教学“乘法分配律”后的思考
浙江省杭州市萧山区党湾二小 萧百奇
“乘法分配律”是继“乘法交换律”和“乘法结合律”之后的又一新的运算定律,它不同于乘法交换律和结合律,是单一的运算,因此,它的抽象程度较高。我们应把握学生的思维规律,以促进他们的思维发展。本文从形象思维的过渡;逆向思维的应用;发散思维的提高这三个方面来进行论述。
形象思维 逆向思维 发散思维
刚上完第八册“运算定律与简便计算”这一单元,不免抱怨多多。从学生的作业情况看,真是错误百出,特别是对“乘法分配律”的运用。那段时间总是觉得现在的学生上课不够专心,思维不够灵活。可后来静下心来一想,也许是自己对教材、对学生的把握不够,“高估”了他们的能力。“乘法分配律”的教学是继“乘法交换律”和“乘法结合律”之后的又一新的运算定律,它不同于乘法交换律和结合律是单一的运算,因此,它的抽象程度较高,是学生学习中的难点。我们应以一颗平常心来反思自己的教学,把握学生的思维规律,使自己在以后的教学中得心应手。以下是我在教学“乘法分配律”后的几点思考:

一、形象思维的过渡
由于“乘法分配律”的抽象程度较高,学生做起题来总是用错乘法分配律的公式,其实这正是说明他们对其本质的不了解,所以我们在教学时应准确地把握和充分利用教材中的直观材料,对具体的事物进行观察、分析与比较,抓住知识的内部联系及其本质特征,再进行抽象概括,这样,使学生的思维由形象到抽象,掌握了本质,乘法分配律就得到了正确的运用。
在教学时,我是这么处理的:上课一开始,我就让学生口算黑板上的几道题。
(1)(6+4)×8=
6×8+4×8=
(2)(3+6)×5=
3×5+6×5=
(3)11×(7+2)=
11×7+11×2=
等学生口算好之后,我就直接让学生观察、比较,然后得出规律,最终得到乘法分配律,自认为学生都该掌握了,可事实上却是自以为是。究其原因,我正是犯了一个“过急”的错,应让学生从形象思维过渡到抽象思维。其实在我让学生口算好之后,应该利用口算题出示例题:求下列图形的面积
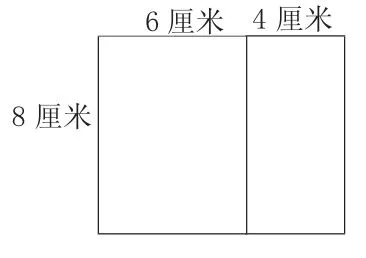
学生完成之后,不难出现口算第一题中的两种求法,然后告诉学生:两种方法求出的都是大长方形的面积。现在老师把这两个算式用等号连接起来,你知道这是为什么吗?这样让学生初步感知到两种不同的计算方法,由于大长方形面积一样,可以用等号连接起来。那么,刚才做的口算题中,都可以用等号连接起来吗?
这是形象思维阶段。学生已经感知到得数相等的两个不同算式可以用等号连接。然后从四个方面引导学生观察比较:(1)在这三个等式中,等号左边的算式有什么相同的地方?等号右边三个算式又有什么相同的地方?(2)相同的因数是等号左边的哪个数?另外两个不同的因数是等号左边的哪两个数?(3)通过这三个算式,你可以发现什么规律?(4)如果用字母a、b、c分别代表任意三个数,可以怎么表示?这样就使乘法分配律深入人心,学生了解了其本质,并从个别问题上升到了一般规律。
二、逆向思维的应用
在改作业时经常碰到这样的学生,在算(a+b)×c时能很快用上乘法分配律a×c+b×c,可在算a×c+b×c时,就往往按部就班地先算乘后算加,却不知道逆向思维用上(a+b)×c,其实这也是乘法分配律。教学中如能把握这种双向思维,在顺推之后进行逆推,而且更为注重逆推能力的训练,则思维必然灵活,所学知识必然又快又活,也容易促使学生形成良好的认知结构。
教学时,我在学生学完(a+b)×c=a×c+b×c后,没有再深入地让学生利用逆向思维进行思考,导致了部分学生思维受到限制,觉得非常可惜。其实在学生概括出乘法分配律时,我们可以适时地将(6+4)×8=6×8+4×8对调成6×8+4× 8=(6+4)×8,然后问学生:这样可以吗?
由此可以得出:两个数分别与同一个数相乘再相加,可以先求出两个不同因数的和,再与相同的那个因数相乘,即a×c+b×c=(a+b)×c。学生通过这样的思维训练,认识到了思维的可逆性,在思维上得到了提高和发展,做题目也会更加灵活。以至于在之后教学a-bc=a-(b+c)时,学生就会运用逆向思维,知道了a-(b+c)=a-b-c,就不会出现a-(b+ c)=a-b+c直接将括号去掉这种错误的情况了。
三、发散思维的提高
一次学生拿着一道题来问我:55× 101=55×100+55是用了什么运算定律?我就只知道用了简便方法。我笑着告诉他,其实这就是乘法分配律啊!将101看成100+1,再运用乘法分配律不就变成了右边的式子。在用简便方法时,学生可利用乘法分配律进行新的多向性探求问题的思维,是创造性思维的基础。在教学中,老师应告诫学生,要善于独立思考,从多方面去探索解题途径,进行一题多解,一题多问,一题多变等多向性的训练。
例如:计算65×99,可将99看成100-1,也可将99看成90+9;计算25× 44,可将44看成40+4,也可将44看成4×11。其中在计算 65×99=65×(100-1)=65×100-65×1时,教师可以设疑,请学生解释为什么差也适合用上乘法分配律。再通过对具体等式的解释到概括两个数的差与一个数相乘的运算规律。学生经历了思考、表达交流、提升认识的过程,自然拓展了对乘法分配律的认识和应用。在简便计算时,不免算法多样,但在算法多样化的同时,也要考虑到算法的优化。例如在解决125×72时,很多同学由于受到前面乘法分配律的影响,会将72看成70+2来做,虽然给解题带来一些方便,可若将72看成8×9,那不是更方便吗?对于算法优化,我们应鼓励,引导学生对算法进行分析,比较,但不要强求,应该把优化的过程作为一个引导学生主动寻找更好方法的过程,尊重每一个学生的选择。
教学是个永无止境的过程,发展学生的思维能力同样也是一个长期而艰巨的过程,我们在平时的教学中要学会反思,把握思维规律,促进学生的思维发展,使教学更有效。
[1]小学数学新课程标准
[2]小学数学教师.2007年第三期
[3]数学方法入门
