稀疏圆阵的解相干求根MUSIC算法
2016-03-13,,,
, , ,
(空军预警学院, 湖北武汉 430019)
0 引言
均匀圆阵(Uniform Circular Array, UCA)在雷达、声纳和无线通信等领域应用日益广泛,这是因为相比于常规的均匀线阵,UCA具有可以同时提供俯仰角和方位角信息、方向图在任何方位上具有基本相同的波束形状和圆阵天线更易实现共形等优势[1-2]。UCA的超分辨DOA(Direction of Arrival)估计算法主要包括阵元域直接处理和波束域处理两类。在阵元域直接处理时,由于UCA导向矢量不具备范德蒙德结构,因此无法使用root-MUSIC, ESPRIT等算法减少运算量,以及平滑处理、矩阵重构等方法解相干。文献[3]研究了两种不同放置方式的圆阵的分辨特性,文献[4-5]提出了直接利用圆阵的特殊阵列设置实现对相干源的DOA估计,不过这类算法的解相干性能和阵列设置的结构密切相关,而且没有考虑阵列稀疏的情况。
波束域处理通常采用波束变换的方法得到具有范德蒙德结构的波束域导向矢量。阵列内插变换[6]和相位模式激励方法[7]是UCA波束变换的常用方法,前者适用于较小方位区域的处理,增加处理方位的范围会导致误差增大;后者利用空间离散傅里叶变换,适用于全方位处理,在阵元数目足够多的情况下,波束域导向矢量可以看作具有共轭对称和范德蒙德结构。以相位模式激励方法为基础,文献[8]提出了UCA-RB-MUSIC,UCA-ESPRIT算法,文献[9-10]提出了Unitary root-MUSIC算法,这些算法在波束域进行处理,避免了谱搜索过程,降低了计算量;文献[11-14]提出了针对相干源的圆阵波束域DOA估计算法,这些算法利用波束域导向矢量的共轭对称和范德蒙德结构,通过矩阵重构实现了对相干源的解相干。但是,以上算法的适用范围是阵元数大于2K(K是最大模式值,与圆阵半径和信号频率的乘积成正比),当阵元数减少,即阵列稀疏时会产生很大误差,导致上述算法失效。为了解决稀疏圆阵的DOA估计问题,文献[15]定量分析了相位模式激励类算法的误差,并且提出了一种改进的波束变换方法,通过循环迭代的方式可以消除误差的主要部分,从而使波束域导向矢量更加接近理想的共轭对称和范德蒙德结构。文献[16]提出的sparse UCA root-MUSIC(SR)算法则是不改变相位模式激励的变换矩阵,而对波束域的导向矢量进行误差补偿,从而消除误差的主要部分。文献[15]中的方法复杂度较高,需要信号方位的先验信息,而且在阵元数小于K时只能消除部分误差,导致算法性能急剧下降,因此只适用于阵元数大于K的情况。SR算法理论上适用于任意阵元数的UCA,但是得到的波束域导向矢量不再具有共轭对称或者范德蒙德结构,无法使用平滑、前后向平均等解相干方法。
本文在SR算法的基础上,首先改进了波束变换矩阵,对变换矩阵进行相位校正,从而使波束域导向矢量具备了共轭对称结构,进而提出了稀疏圆阵的解相干求根MUSIC算法(Sparse UCA Decorrelation Root-MUSIC , SDR),这种算法适用于任意阵元数的UCA,而且进行了前后向平均处理,可以实现对相干信号源的DOA估计,在低信噪比和低快拍数情况下有更好的估计性能。

1 阵列模型
这里只考虑入射信号与阵列在同一个平面的情况,假设均匀圆阵由M个各向同性的阵元组成,圆阵水平放置,半径为r。以圆心为参考点,则阵列的导向矢量可以表示为
a(θ)=[e-j2πr/λ cos(θ-γ1), e-j2πr/λ cos(θ-γ2),…,e-j2πr/λ cos(θ-γM)]T
(1)
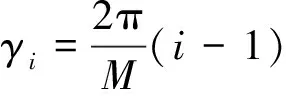
阵元的接收数据可以表示为
x(t) =As(t)+n(t)
(2)
式中,A=[a(θ1),a(θ2),…,a(θN)]为N个信号的阵列流形,s(t)为N×1维的信号矢量,n(t)为M×1维的噪声矢量,x(t)为M×1维的阵元接收数据矢量。
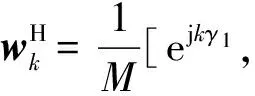
bkejkθ+Δ
(3)

b(θ)≈FaB(θ)=
[b-Ke-jKθ,b-(K-1)e-j(K-1)θ,…,bKejKθ]T
(4)
式中,F=diag([b-K,b-(K-1),…,bK]),aB(θ)=[e-jKθ,e-j(K-1)θ,…,ejKθ]T。
常规相位模式激励法以F-1W=F-1[w-K,w-(K-1),…,wK]H作为波束形成器,那么aB(θ)即为波束域导向矢量,具备共轭对称和范德蒙德结构,可以使用平滑处理及矩阵重构等方法解相干[12-15]。
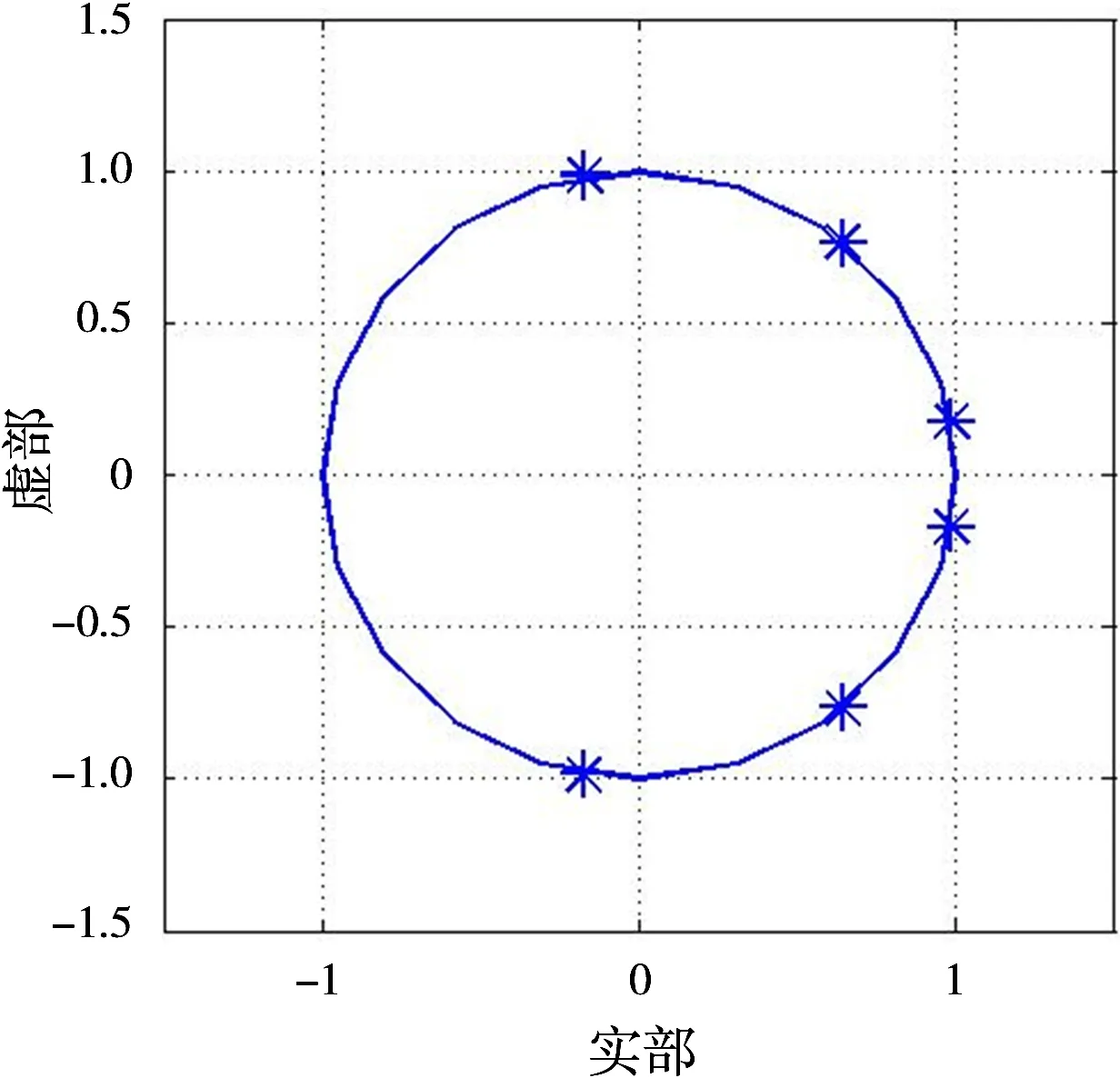
SR算法以W作为波束形成器,考虑阵元数为奇数且M<2K的阵列稀疏情况,记P=(M-1)/2,取|k|≤P,此时Δ中存在P<|k±qM| |k±qM| co(θ)=Hob(θ) (5) 式中,Ho=[I1⋮I⋮Ir],I为(2P+1)×(2P+1)维的单位矩阵,Il为I的后K-P列,Ir为I的前K-P列。显而易见,这种方法得到的波束域维数为2P+1,将P<|k±qM| 对于补偿后的导向矢量仍然可以进行root-MUSIC运算,避免了计算量较大的谱搜索过程。上面提到的补偿矩阵Ho的形式只适用于K<3P+1的情形,当阵元数继续减少时,文献[17]给出了补偿矩阵相应的形式,在3P+1 SR算法改进了传统的相位模式激励方法,适用于阵元稀疏的情况,而且可以采用root-MUSIC方法减少计算量。但是它的缺陷在于不适用于相干信号源的DOA估计,而实际应用中,由于多径等情况的存在,相干信号源是不可避免的。SR算法不能解相干的原因是它的波束域导向矢量co(θ)不再具有共轭对称或者范德蒙德结构,因此,首先考虑改进SR算法,得到具有共轭对称结构的波束域导向矢量。 这里考虑阵元数目为偶数的情况,即M=2P,同样地,P He=[0l⋮I⋮0r]+[Il⋮0⋮Ir] (6) 式中,0l和0r都为(2P+1)×(K-P)维的零矩阵,I为(2P+1)×(2P+1)维的单位矩阵,Il为I的后K-P+1列,Ir为I的前K-P+1列,0为(2P+1)×(2P-1)维的零矩阵。 可以看出,当阵元数目为偶数时,补偿矩阵有别于阵元数目为奇数的情况。下面讨论这两种情况下波束域的特征。为了直观地说明问题,这里取K=5,P=3。首先得出阵元数目M=6和M=7两种情况下的补偿矩阵。 (7) 相应的波束域导向矢量为 (8) 观察以上两种情况下的波束域导向矢量可以看出: 1)ce(θ)的首末两项是重复的,其中一个是冗余的,co(θ)则无冗余,也就是ce(θ)的有效维数为M。这是由于补偿后的波束域是2P+1维的,当阵元数为2P时,少于波束域维数。 3)ce(θ)的元素中相加项的下标同为奇数或者同为偶数,而co(θ)的元素中相加项的下标为一奇数一偶数。 在上述观察结果的基础上,为了使波束域导向矢量具有共轭对称结构,再考虑bk=jkJk T=diag([(-1)P,(-1)P-1,…,(-1)0,1,…,1]) (9) 综上所述,新的波束形成器是TW,对应的波束域导向矢量d(θ)满足共轭对称结构,表示为 d(θ)=Tce(θ)=THeFaB(θ) (10) 通过前一小节所述的改进波束变换方法,可以得到具有共轭对称结构的波束域导向矢量,从而可以利用前后向平均处理的方法,实现对相干源的DOA估计。需要说明的是,这种方法针对的是时域相位不一致的相干信号,即信号的相位差非零且非π的情况,实际中的相干源基本上都满足这一要求。 首先,介绍波束域前后向平均处理的方法,采用前一节提出的波束变换方法后,可以得到波束域数据: y(t)=TWx(t)=TWAs(t)+TWn(t)= Ds(t)+TWn(t) (11) 式中,D=[d(θ1)d(θ2)…d(θN)]。相应的波束域数据协方差矩阵可以表示为 R= E [y(t)yH(t)] (12) 然后,可以进行前后向平均处理: (13) 式中,J为(2P+1)×(2P+1)维的反对角线单位矩阵。 (14) 令z=ejθ,可得出关于z的2P阶方程,通过对方程求根即可得出相干信号源的DOA。 R=DE [s(t)s*(t)]DH+TWE [n(t)n*(t)]WHTH= (15) (16) ρ*ρT),下面对它进一步求解: (17) 式中,P=[ρρ*],P又可以表示为 (18) 很明显可以得到,在|angle(ρ(1))-angle(ρ(2))| 实验中,圆阵半径r=λ, 最大模式值为K= 图1 r=λ情况下|bk|与k的关系图 实验1:不同阵元数时的解相干性能 实验仿真比较本文算法与文献[13]中MODETOEP算法及MODEFBSS算法在不同阵元数情况下的解相干性能。实验中阵元数目分别为16,10和6,其中,阵元数16是阵列不稀疏的情况,阵元数10和6分别是阵元数目大于和小于最大模式K的阵列稀疏的情况, 3种阵元数目分别对应阵元间距为0.39λ,0.63λ和1.05λ。两个相干信号入射方位分别为-20°和20°,衰落系数分别为1,0.9ej1.3。其中,MODETOEP算法和MODEFBSS算法需要采用传统的相位模式激励法,波束域维数为15,波束域导向矢量采用aB(θ),MODEFBSS算法子阵阵元数为10;本文算法波束域维数分别为17,11和7,波束域导向矢量采用d(θ)。实验结果由200次蒙特卡洛仿真得出,快拍次数为100。图2是16元阵3种算法的解相干性能,图3是10元阵和6元阵使用本文算法的解相干性能。 当阵元数为16时,3种算法均有效,但是MODETOEP算法估计偏差始终为11°左右,估计精度较差,这是因为MODETOEP等矩阵重构类算法适用范围是ρ为实数矢量,当ρ为复数矢量时,会引起估计角度的偏移。随着信噪比增大,本文算法和MODEFBSS算法估计偏差逐渐减小。在信噪比小于0 dB时,很明显本文算法估计精度好于MODEFBSS算法,这是由于本文算法考虑了|k+qM|<11的所有误差,而MODEFBSS算法需要忽略9<|k±qM|<11的误差。 当阵元数为6或者10,即阵列稀疏时,MODETOEP算法和MODEFBSS算法失效,无法正确估计出信号源方位,因为这两种算法要求波束域导向矢量满足范德蒙德结构,然而阵列稀疏时相位模式激励有较大误差,波束域导向矢量并不满足范德蒙德结构。本文算法由于考虑了模式激励的误差,在阵列稀疏时仍有很好估计性能,当信噪比大于-5 dB时,估计偏差小于1°,估计精度好于16元阵的MODEFBSS算法。 实验2:稀疏阵列对非相关信号源估计性能 实验仿真对于阵元数为6的稀疏UCA,比较不同快拍数和不同信噪比时本文算法与SR算法对于信号的估计性能。实验中,采用两个不相关信号,入射角度分别为-10°和10°,比较信噪比的影响时快拍数为50,比较快拍数影响时,信噪比为-3 dB。当估计方位与目标真实方位相差小于0.1倍的目标方位间距时,认为估计成功。实验结果由200次蒙特卡洛仿真得出。 从图4中可以看出,在快拍数大于150或者信噪比大于0 dB时,本文算法与SR算法估计性能基本一致,但是当快拍数小于150或者信噪比小于0 dB时,本文算法成功概率和RMSE都要优于SR算法。这是因为本文算法通过改进波束变换矩阵,增加了平滑处理,具有平均的意义。 (a)成功概率与信噪比的关系 (b)估计偏差与信噪比的关系图2 16元阵3种算法解相干性能 (a)成功概率与信噪比的关系 (b)估计偏差与信噪比的关系图3 10阵和6元阵使用本文算法的解相干性能 (a)成功概率与信噪比的关系 (b)RMSE与信噪比的关系 (c)成功概率与快拍数的关系 (d)RMSE与快拍数的关系图4 稀疏阵列的估计性能 实验3:稀疏阵列的解相干能力 实验仿真阵元数为6和8的两种稀疏圆阵,其中针对6元阵仿真了1组和2组相干源的情况,针对8元阵仿真了2组和3组相干源的情况。其中各组相干源入射角度分别是(10°,-10°),(50°,-50°)和(100°,-100°)。实验快拍数为100,信噪比为0 dB。图5和图6为利用本文算法求解所得根的分布,其中横轴表示根的实部,纵轴表示根的虚部,与横轴正方向的夹角即为估计的入射信号方位角。 (a)1组相干源 (b)2组相干源图5 6元阵根分布图 (a)1组相干源 (b)2组相干源 (c)3组相干源图6 8元阵根分布图 从图5和图6可以看出,6元阵和8元阵分别可以估计出4个相干源和6个相干源的入射方位。理论上,对于M元阵,在波束域有M个有效的自由度,可以估计M-1个相干源,然而实际中由于噪声等因素的影响,在对M-1个相干源估计时会出现多个虚假方位,导致估计失败,最多只能估计出M-2个相干源。 本文首先在SR算法的基础上,对波束变换过程中的误差进行补偿,得到了波束域导向矢量的正确表达形式,相比传统的相位模式激励方法要求阵元数大于2K,该方法适用于阵元数小于2K的稀疏圆阵。然后,通过分析新的波束域导向矢量的结构特征,提出对波束域进行相位校正的方法,从而实现了波束域导向矢量的共轭对称结构。最后,利用这种共轭对称结构进行前后向平均,实现了对相干信号源的解相干。 相比其他的圆阵波束域解相干算法,该方法考虑了波束变换的误差,从而不再需要阵元数目大于2K,在阵列稀疏的情况下仍然具有较高的估计精度。与阵元域处理算法相比,本文算法可以采用root-MUSIC算法,避免了谱搜索过程,减少了计算量。 [1] JACKSON B R, RAJAN S, LIAO B J, et al. Direction of Arrival Estimation Using Directive Antennas in Uniform Circular Arrays[J]. IEEE Trans on Antennas and Propagation, 2015, 63(2):736-747. [2] WANG P, LI Y H, VUCETIC B. Millimeter Wave Communications with Symmetric Uniform Circular Antennas Arrays[J]. IEEE Communications Letters, 2014, 18(8):1307-1310. [3] 吴垚,陈辉. 两种均匀圆阵特性对比分析研究[J]. 雷达科学与技术, 2011, 9(1):62-66. WU Yao, CHEN Hui. Comparison and Analysis of Characteristics of Two Different Uniform Circular Arrays[J]. Radar Science and Technology, 2011, 9(1):62-66.(in Chinese) [4] WU Y, CHEN H, CHEN Y C. A Method of 2-D DOA Estimation of Coherent Signals Based on Uniform Circular Array via Spatial Smoothing[C]∥CIE International Radar Conference, Chengdu:IEEE, 2011:312-314. [5] CHEN H, ZHAO M. A Modified Method of the Wideband Coherent Signals DOA Estimation on the Uniform Circular Arrays[C]∥2nd International Conference on Electronics, Communications and Control, Zhoushan:IEEE, 2012:3166-3169. [6] 蒋柏峰,吕晓德. 一种基于导向矢量变换的DOA估计预处理方法[J]. 电子与信息学报, 2012, 34(7):1552-1557. [7] DAVIES D. A Transformation Between the Phasing Techniques Required for Linear and Circular Aerial Arrays[J]. IET Proceedings of the Institution Electrical Engineers, 1965, 112(11):2041-2045. [8] MATHEWS C P, ZOLTOWSKI M D. Eigenstructure Techniques for 2-D Angle Estimation with Uniform Circular Arrays[J]. IEEE Trans on Signal Processing, 1994, 42(9):2395-2407. [9] BELLONI F, KOIVUNEN V. Unitary Root-MUSIC Technique for Uniform Circular Array[C]∥IEEE International Symposium on Signal Processing and Information Technology, Darmstadt, Germany:IEEE, 2003:451-454. [10] QIAN C, HUANG L, SO H C. Improved Unitary Root-MUSIC for DOA Estimation Based on Pseudo-Noise Resampling[J]. IEEE Signal Processing Letters, 2014, 21(2):140-144. [11] HAN Yong, GAO Bingxia, DONG Wenyi, et al. An Improved Mode-MUSIC Algorithm for DOA Estimation of Coherent Sources Based on Hybrid Array[C]∥International Conference on Signal Processing, Beijing:IEEE, 2014:358-362. [12] GAO Shuyan, CHEN Hui, WANG Yongliang, et al. A Novel Algorithm for Estimating DOA of Coherent Signals on Uniform Circular Array[C]∥CIE International Conference on Radar, Shanghai:IEEE, 2006:1-4. [13] WANG Ju, GU Xiaopeng, LIU Yan. The Coherent DOA Estimation of Uniform Circular Array Based on SVD Algorithm[C]∥International Conference on Electrical and Control Engineering, Yichang:IEEE, 2010:6147-6151. [14] ZHAO Hui, WANG Hongjin. MODE-SUMWE Algorithm for Estimating DOA of Coherent Signals on Uniform Circular Array[C]∥International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan:IEEE, 2010:318-320. [15] BELLOIN F, KOIVUNNEN V. Beamspace Transform for UCA:Error Analysis and Bias Reduction[J]. IEEE Trans on Signal Processing, 2006, 54(8):3078-3089. [16] GOOSSENS R, ROGIER H, WERBROUCK S. UCA Root-MUSIC with Sparse Uniform Circular Arrays[J]. IEEE Trans on Signal Processing, 2008, 56(8):4095-4099. [17] 王永良,陈辉,彭应宁,等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004:346-349.2 改进的波束变换和平滑方法
2.1 改进的波束变换方法


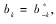
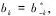
2.2 波束域前后向平滑处理

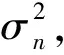


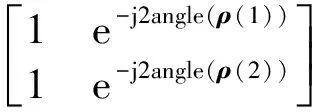
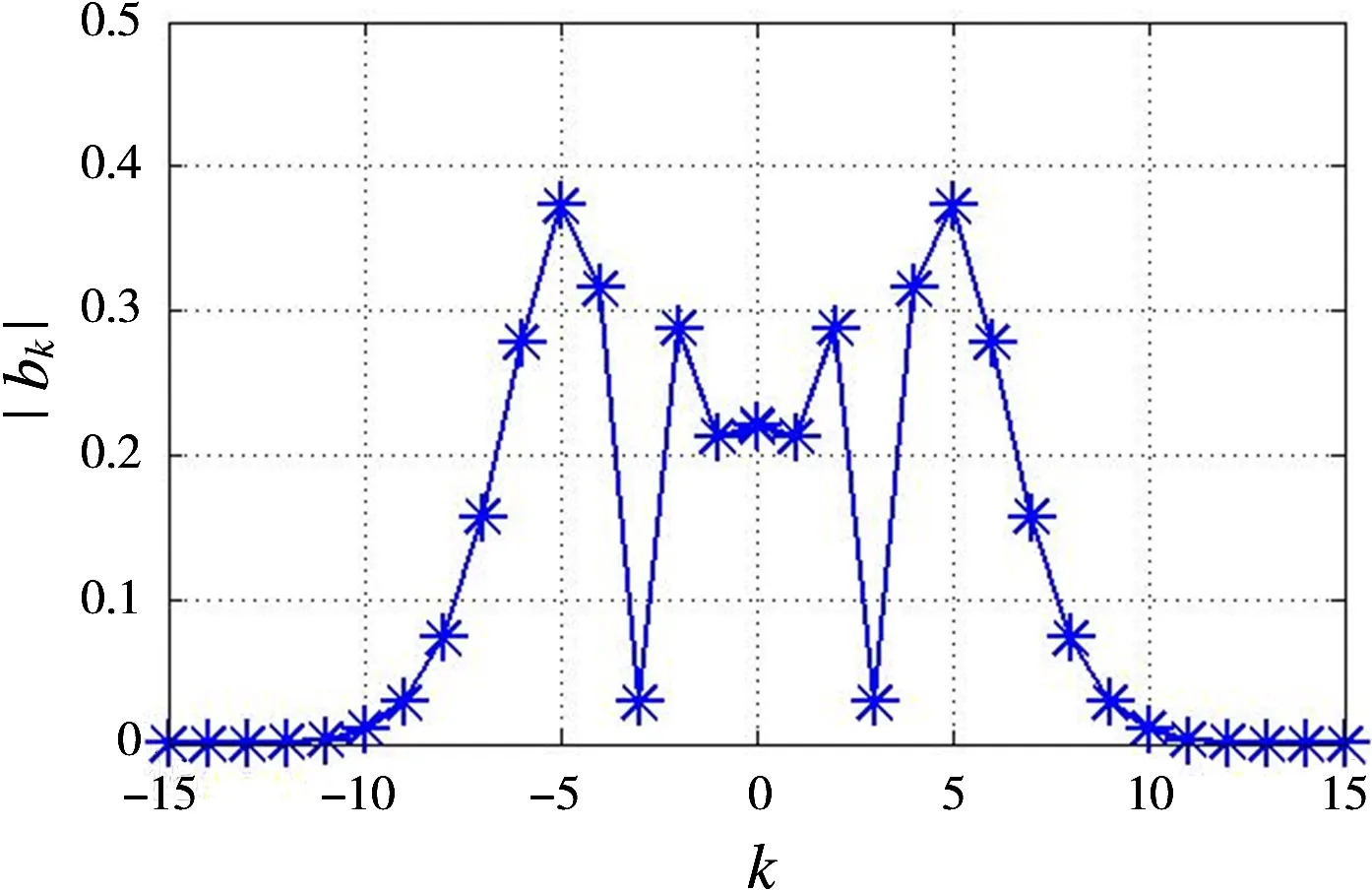
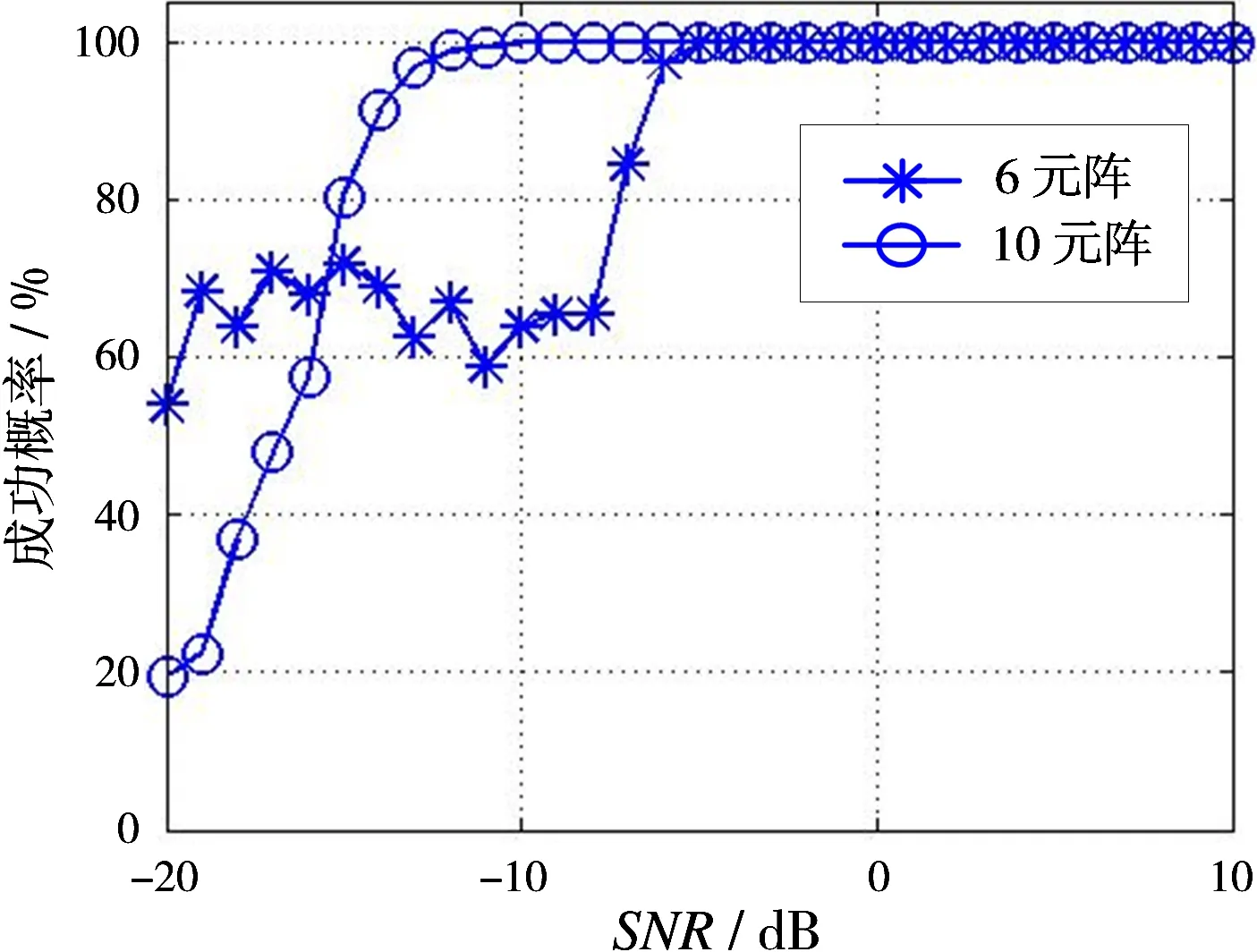
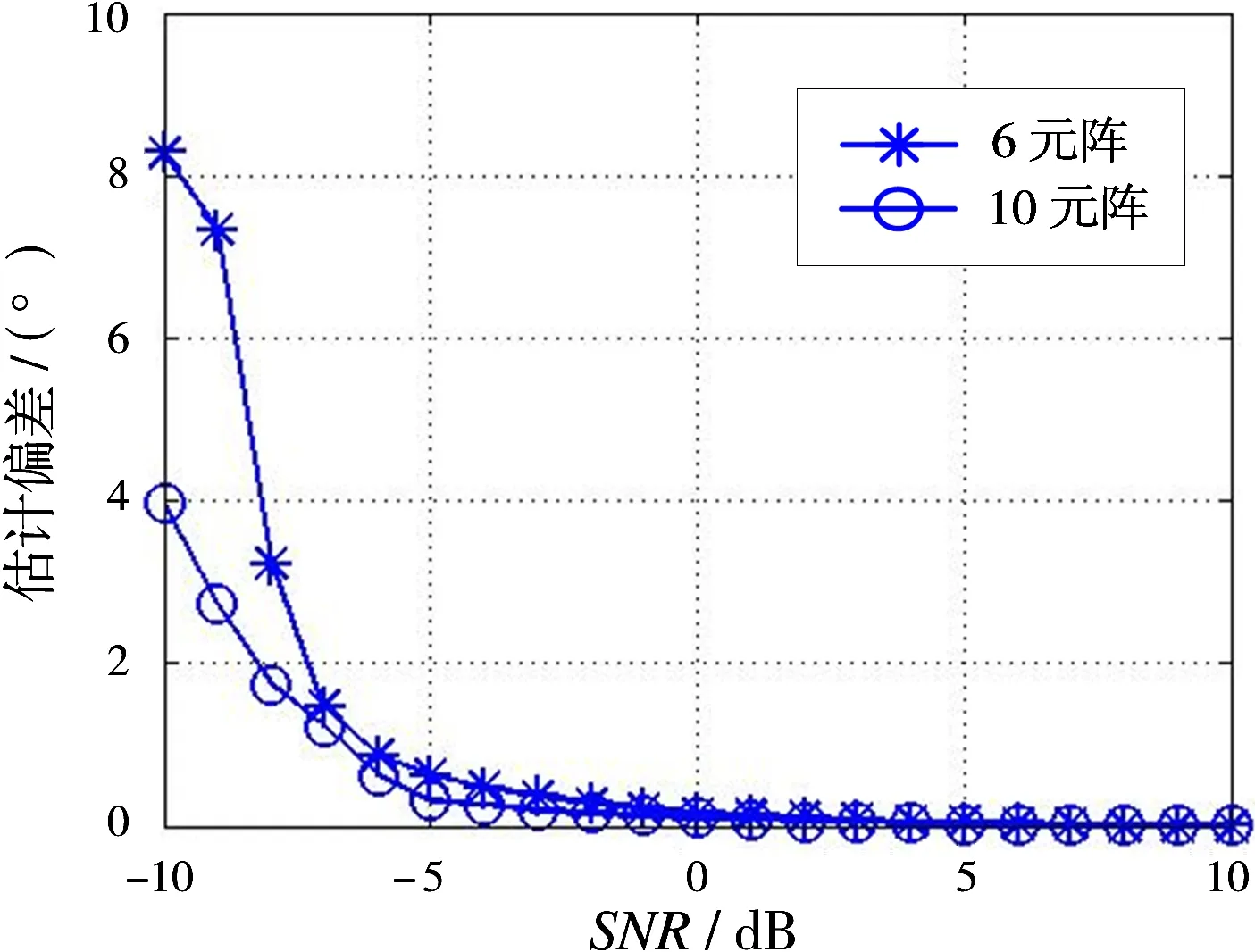
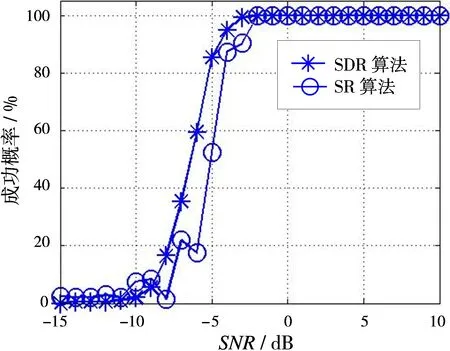
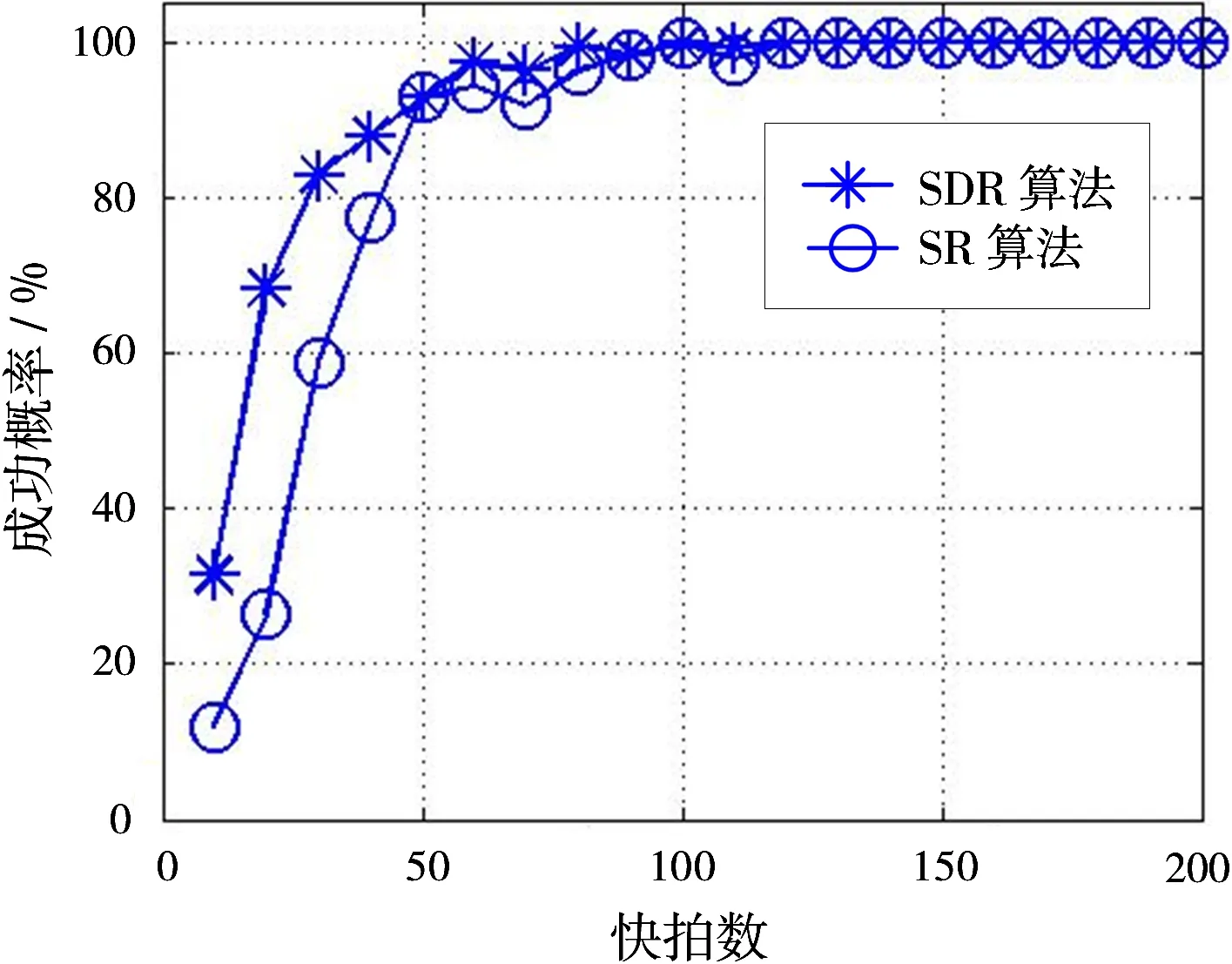
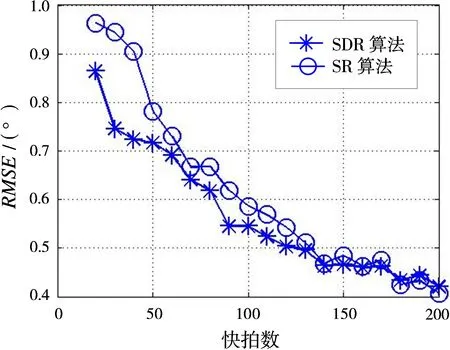
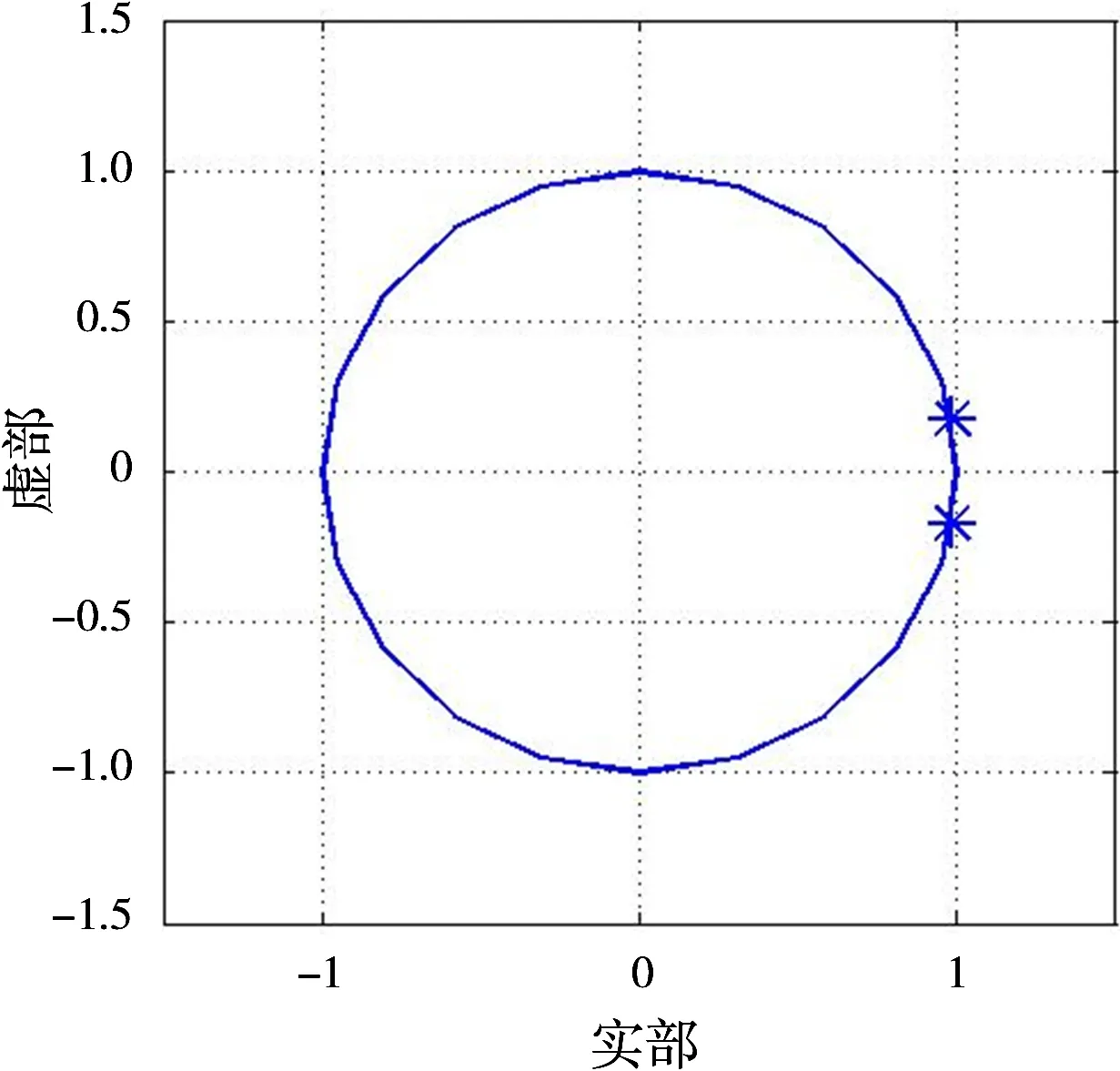
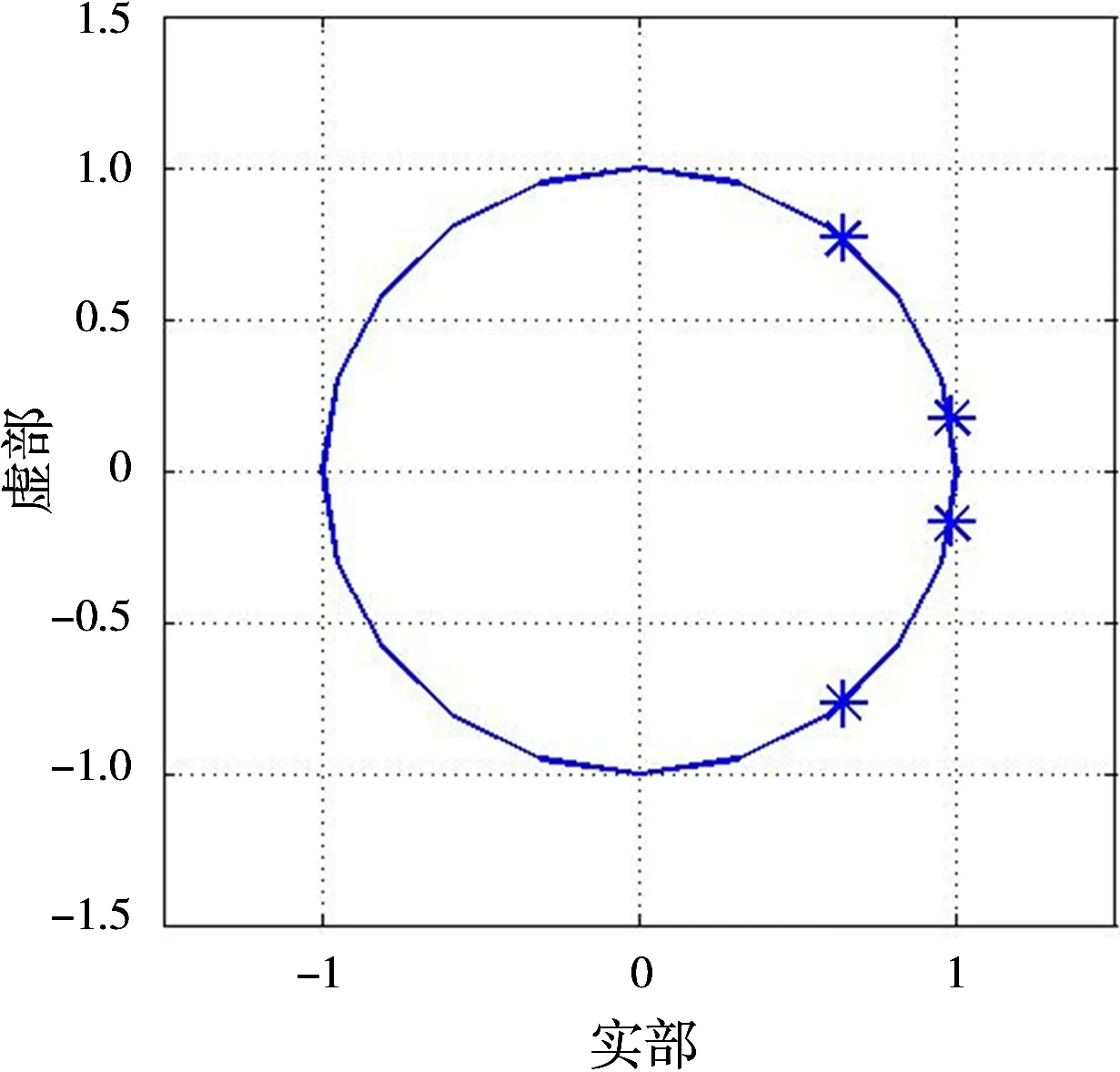
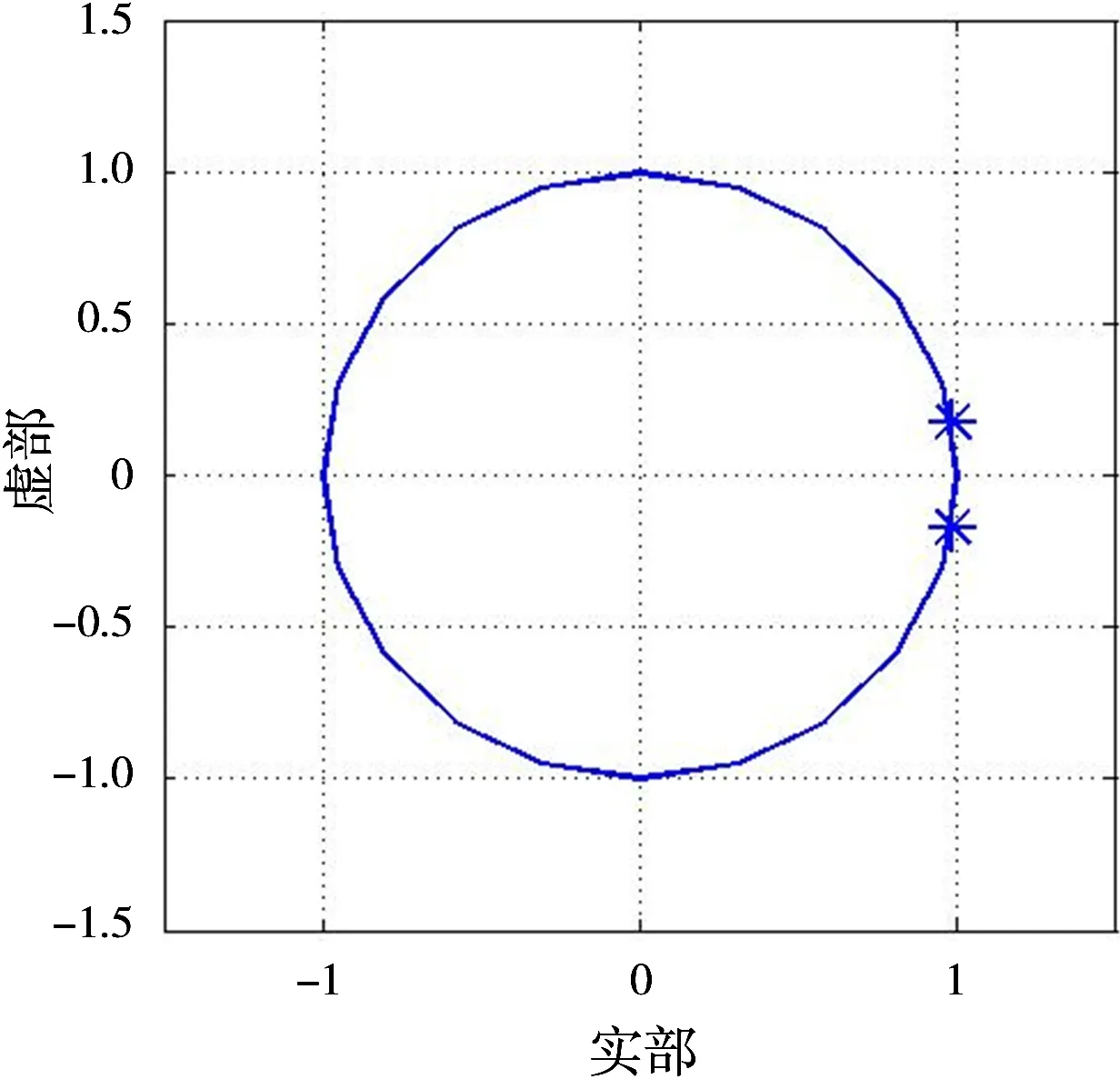
3 仿真分析


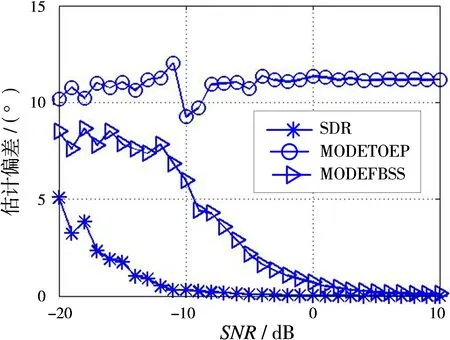


4 结束语
