数据场和K-Means算法融合的雷达信号分选

， ， ，

(中国人民解放军93199部队， 黑龙江哈尔滨 150001)

0 引言

雷达信号分选是雷达侦察系统中信号处理的核心部分之一，只有从交叠信号流中分选出各个辐射源脉冲序列之后才能进行信号参数的测量、分析、识别以及对威胁辐射源施加干扰。传统采用脉冲重复间隔(PRI)单参数分选的正确率较低，已经不能适应当前复杂的电磁环境。聚类分析作为数据挖掘中的一种重要技术，近年来成为众多学者研究的热点，有很多学者尝试着将其应用于雷达信号分选领域，取得了一些成绩。国内学者在聚类分选方法上也作了不少研究，代表性的有许丹[1]探讨了在单站无源定位条件下当测角精度不高时的信号分选问题，提出了一种二次聚类方法。2005年我国著名信号分选专家祝正威提出了一种针对未知雷达信号的加权动态聚类分选算法[2]，该方法虽然在一定程度上解决了密集复杂脉冲信号的分选问题，但是仍然无法解决长期以来一直面临的“容差”问题。另外，文献[3-6]中分别研究了基于模糊聚类、BFSN聚类、基于分段聚类和基于网格聚类在雷达信号分选中的应用。张万军使用K-Means聚类对参数相近、互相交叠的非常规雷达信号进行分选，效果较好、速度快，但是K-Means聚类算法需要先验知识，不适合未知雷达信号的分选。

针对K-Means聚类算法的缺陷，本文提出了一种融合算法，将数据场算法与其相结合，利用数据场对雷达数据流进行初分选，得到初始的聚类中心和聚类数目，然后利用K-Means聚类完成最后的分选。

1 K-Means聚类算法原理

K-Means聚类算法由MacQueen首先提出，属于聚类方法中一种基于划分的方法，它是一种较简单的迭代优化方法。该算法的数学描述如下：

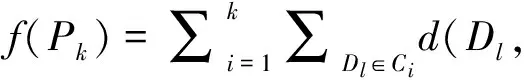
这种聚类算法的特点是：每个类都是全体数据对象的一个子集或者真子集，其中每个数据对象到定义该类的聚类中心的距离比到其他类聚类中心的距离更近，在已知聚类个数k的情况下，对样本集合进行聚类，聚类的结果由k个聚类中心来表达，基于给定的聚类目标函数或者说是聚类效果判别准则，算法采用迭代更新的方法，每一次迭代过程都是向目标函数值减小的方向进行，最终达到较好的聚类效果。

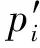
2 数据场聚类原理

李德毅院士在传统物理场的基础上，提出了基于数据对象的数据场理论。数据场能够合理、客观地展示数据对象间的相互影响和相互作用[7]。该理论[8-9]认为数域空间中每个数据点都是一个有作用域的场，即每个数据点可以作用周围其他数据点，用势函数表示这种作用力。场中数据点之间都通过势函数互相作用，其作用力的大小与两者之间距离成反比。数学描述如下：

图1 K-Means雷达信号聚类分选算法流程图

定义数据场空间Ω∈Rn，其空间Ω为包含n个对象的数据集D={x1,x2,x3,…,xn}及其产生的数据场。设数据对象的位置矢量分别为x1,x2,x3,…,xn，对于Ω中任意一个场点y，其产生的势函数为φ(y)，本文选用的是高斯函数，场强矢量值为F(y)，表示分别如下：

(1)

(2)

式中，‖y-xi‖为点y到xi的距离，本文选择的是欧几里得距离；mi≥0(i=1,2,3,…,n)为对象xi的质量，这里简化为单位质点即mi=1；δ为辐射因子，用于控制对象间的作用力程。在空间Ω中，由于数据点势函数的存在，数据点间在无外力作用下会发生相向运动，但受δ的约束，δ越大，所有数据点的影响力越大，辐射范围的影响也越大，则数据场的视图越能体现所有数据点所产生势场的总体效果；δ越小，所有数据点的影响力越小，辐射范围的影响也越小，则数据场的视图越能体现每个数据点所单独产生影响的效果。

3 融合算法

K-Means聚类算法[10-11]应用到雷达信号分选中，适合处理大量数据，聚类时间短，但是存在需要事先确定初始聚类中心和聚类数目的缺陷。选择的初始聚类中心越接近最终的聚类中心，聚类效果越好，迭代时间越短。而数据场聚类算法恰好无需数据的先验知识就能完成初始聚类，提供K-Means聚类算法所需的先验知识。针对两种算法的特点，本文将两种聚类算法相结合，首先利用数据场聚类数目作为K-Means的初始聚类数目，数据场聚类得到的势中心作为K-Means聚类算法的初始聚类中心，最后由K-Means聚类算法完成最后的聚类。

1) 雷达数据标准化

在实际的雷达信号分选中，收到的雷达信号数据流往往比较复杂，不同参数往往不在同一数量级上[12]。为了消除原始数据对分选的影响，需要对雷达信号数据流进行预处理，使其分布在[0,1]之间，以相同数量级进行分选。

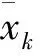
(3)

(4)

2) 雷达信号分选的流程

① 初始化算法参数；

② 读入雷达脉冲数据，提取雷达信号参数脉动到达角DOA、脉冲载频RF和脉冲宽度PW进行数据标准化处理；

③ 利用数据场聚类进行初始的聚类，得到聚类数目和势中心；

④ 利用K-Means聚类算法进行聚类，输出结果。

4 仿真实验分析

为了验证本文提出的融合算法是否有效，仿真实验模拟了3部复杂体制的雷达数据，按照到达时间进行混合，对同时到达的信号进行丢失处理，共得到230个脉冲信号。实际接收的雷达数据与接收机接收的数据有不可避免的测量误差，所以在模拟雷达数据时，给每个参数加上一个随机偏差，参数的偏差均在1%以内。模拟的雷达信号参数如表1所示。

表1 雷达仿真数据

3部雷达混合数据经过标准化处理后，分布如图2所示(图中“*”代表雷达脉冲)。

图2 雷达混合数据三维属性分布图

经过数据场聚类初分选后的效果如图3所示。

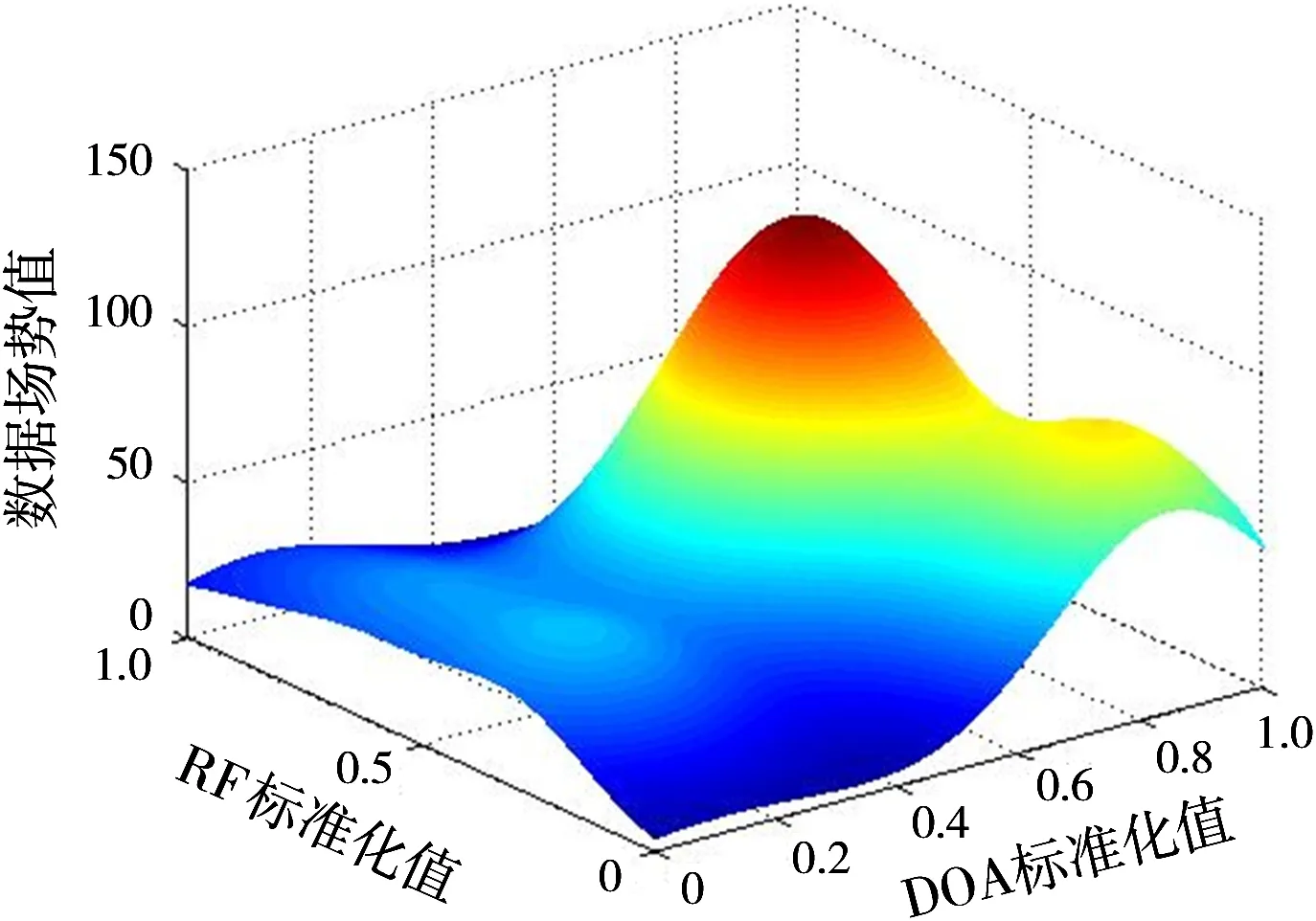
(a)RF-DOA数据场势图

(b)PRI-DOA数据场势图

(c)PRI-RF数据场势图图3 数据场聚类初分选效果图

经过K-Means最后聚类分选效果如图4所示，图中不同形状代表了聚类后的不同雷达数据。

(a)雷达混合数据分选效果分布图

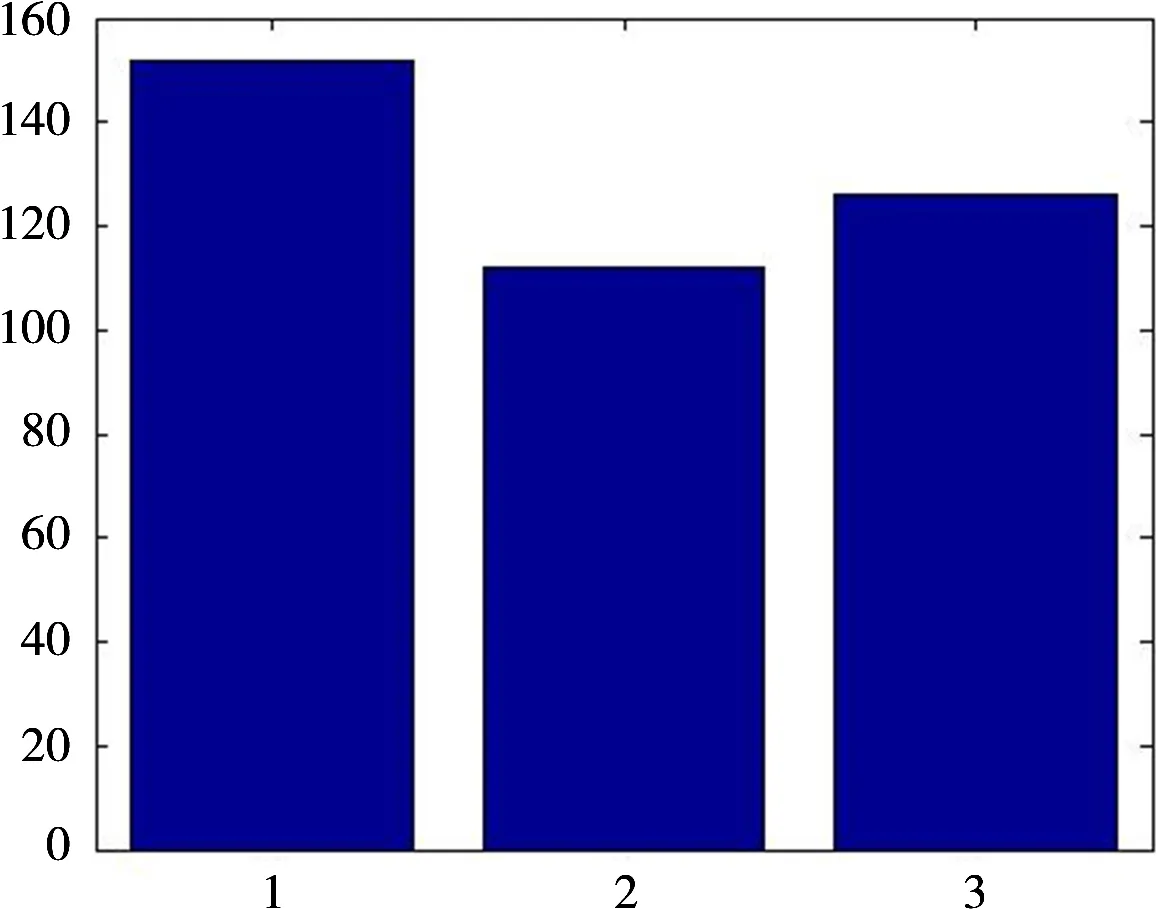
(b)分选数据统计结果图4 融合算法雷达信号分选效果图

由图4分析可以发现，本文提出的融合聚类算法将雷达B中的10个脉冲误分选为雷达A，与雷达A的脉冲一起标记为雷达A；将雷达B中的30个脉冲误分选为雷达C，其余脉冲均分选正确。统计后算得分选正确率为89.74%。

本文将同组雷达数据利用数据场聚类算法和K-Means聚类算法进行了处理，对比结果如表2所示。

表2 分选算法对比结果

由于K-Means聚类算法需要事先给定好聚类数目，而且初始值的选定对聚类结果影响很大，所以本实验对K-Means进行了100次实验得到的数据均为平均值。

由表2可以看出，K-Means聚类算法用时最短，但是其平均聚类准确率比较低；融合分选算法在3种算法中准确率最高，用时最多。

5 结束语

本文将数据场引入到雷达信号分选中，将其与K-Means聚类算法相结合，利用了数据场无需先验知识聚类的优势。经过本文的仿真实验验证，本文提出的融合算法对复杂的雷达信号具有良好的分选效果，具有一定的应用价值，缺点是分选时间较长。本文只是针对几种特殊体制雷达信号进行了仿真实验，后续还需要加强对其他复杂体制雷达信号的研究。

[1] 许丹,姜文利,周一宇. 辐射源脉冲分选的二次聚类方法[J]. 航天电子对抗, 2004(3):26-29.

[2] 祝正威. 雷达信号的聚类分选方法[J]. 电子对抗, 2005(6):6-10.

[3] 王勇刚. 基于模糊聚类的雷达信号分选方法[J]. 电子对抗, 2007(2):9-12.

[4] 叶菲,罗景青. 基于BFSN聚类的雷达信号分选与特征提取算法[J]. 舰船电子对抗, 2005, 28(3):29-34.

[5] 国强,王常虹,郭立民,等. 分段聚类在雷达信号分选中的应用[J]. 北京邮电大学学报, 2008, 31(2):132-135.

[6] 詹磊,唐爱华. 基于多维加权聚类的雷达信号分选方法[J]. 遥测遥控, 2007, 28(S1):113-117.

[7] 陈少达,夏士雄,王志晓. 基于改进谱聚类的提升机故障诊断算法[J].计算机工程与设计, 2015,

36(12):3241-3245.

[8] 刘玉华,张翼,徐翠,等. 一种基于数据场的复杂网络聚类算法[J]. 计算机科学, 2013, 40(11):70-73.

[9] 王丽红,何熊熊. 基于数据场的FCM改进算法[J]. 计算机与现代化, 2014(6):94-97.

[10] YANG Zhutian, WU Zhilu, YIN Zhendong, et al. Hybrid Radar Emitter Recognition Based on Rough K-Means Classifier and Relevance Vector Machine[J]. Sensors, 2013, 13(1):848-864.

[11] 关欣,孙祥威,曹昕莹. 改进的K-Means算法在特征关联中的应用[J]. 雷达科学与技术, 2014, 12(1):81-85.

[12] 赵贵喜,王岩,于冰,等. 基于人工鱼群聚类的雷达信号分选算法[J]. 雷达科学与技术, 2013, 11(4):375-378.