一种火箭及上面级外弹道实时滤波算法

，

(1.宇航动力学国家重点实验室， 陕西西安 710043；2.西安卫星测控中心， 陕西西安 710043)

0 引言

运载火箭上面级[1-2]具有自主导航能力强、推力大、较基础级工作时间长、可多次起动等特点，上面级的使用是提高火箭性能及任务适应能力的有效解决途径。已经在国外的航天发射任务中得到了广泛应用，在我国也受到了越来越多的重视，如某颗新一代北斗导航星的发射即采用了上面级入轨技术。

运载火箭上面级及基础级实时飞行弹道的计算是其飞行过程监视的重要内容，其本质上是一种非线性状态估计[3]问题。这方面应用较多的有扩展卡尔曼滤波[4](Extended Kalman Filter, EKF)、不敏卡尔曼滤波[4-5](Unscented Kalman Filter, UKF)、容积卡尔曼滤波[6](Cubature Kalman Filter, CKF)等。EKF产生较早，它通过非线性模型离散化处理来建立线性化的滤波模型，容易产生高阶截断误差，且常需要计算非线性函数的Jacob矩阵；UKF与CKF使用确定性采样策略来近似函数非线性分布，但UKF在用于高维状态向量估计时，存在计算效率较低、采样点设置参数复杂、数值精度以及稳定性较差的问题。由Ito和Norgaard等人提出的中心差分卡尔曼滤波(Central Difference Kalman Filter, CDKF)算法具有比UKF稍高的理论精度，而且更易于实现，充分考虑了随机变量的噪声统计特性。

为此，本文将中心差分容积卡尔曼滤波引入火箭上面级飞行弹道实时跟踪计算过程中，给出了一种适用于工程实际情况的实时状态估计算法，并通过位置速度与加速度关系对模型方差Q进行自适应调整，以实现滤波对弹道机动过程的自适应跟踪。仿真及实测数据计算结果表明，所给出的计算方法是可行的。

1 中心差分卡尔曼滤波

1.1 中心差分变换算法

中心差分变换是CDKF的基础，其核心思想是通过随机变量的非线性变换求解均值和方差等，具体就是用Sterling差值公式代替泰勒级数展开式中一阶、二阶导数，用多项式逼近非线性方程导数，从而避免了EKF滤波中雅可比矩阵的求导运算[3]，具有实现过程较为简单的特点。

(1)

采用中心差分计算来代替式(1)中一阶、二阶导数项，可得到非线性方程的近似表达式：

(2)

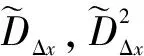
(3)

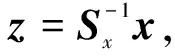
(4)

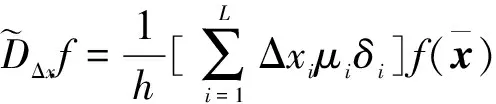
(5)

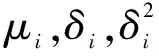
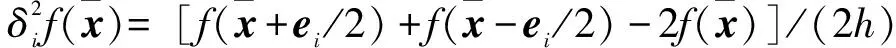
(6)

式中：ei为第i个元素为1，其余元素为0的单位向量；Sxi为Sx的第i个列向量。由式(4)可知：

式中，Sxi为状态协方差矩阵Cholesky分解后的第i列，则可得均值：

(7)

方差为

(8)

协方差为

(9)

1.2 CDKF滤波计算

CDKF实质上是利用基于先验分布构造的Simga点进行线性回归变换来表示状态后验分布的一种采样滤波方法，其基本原理与UKF类似。

设非线性系统为

(10)

式中：xk为k时刻系统状态向量，其维数为L； F为状态向量的转移函数；wk-1为状态向量的高斯过程噪声，其均值为零，协方差矩阵为Qk-1；yk为k时刻的m维观测向量； H为观测函数；vk为高斯量测噪声，协方差矩阵为Rk。则该非线性估计的CDKF滤波算法主要有以下步骤：

1) 构造时间更新所需采样点

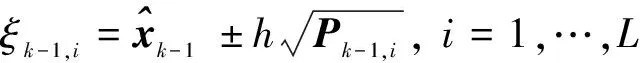
(11)

其变换权系数为

Wx,0=(h2-L)/h2

Wx,i=1/(2h2),i=1,…,2L

(12)

2) 进行时间更新

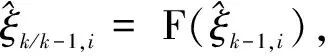
(13)

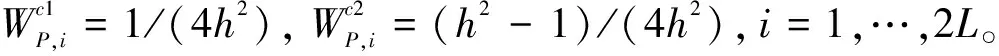
3) 构造量测更新所需的采样点集

(14)

4) 量测更新计算

(15)

量测与状态的互协方差阵：

(16)

5) 计算残差

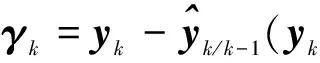
6) 进行状态更新

考虑到在上面级机动飞行中，滤波计算过程有一定的舍入误差，以及初值误差可能较大，从而可能导致滤波出现发散现象。为此，在中心差分滤波实现中，在上面的误差协方差阵递推计算中常采用平方根代替协方差矩阵进行递推计算，从而可得到平方根中心差分卡尔曼滤波(SRCDKF)。

2 火箭及上面级弹道滤波模型

2.1 观测方程及系统状态方程

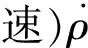
rE=(HG)r

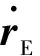
HG=(EP)(ER)(NR)(PR)

HDG=(EP)(EDR)(NR)(PR)

(17)

式中，PR为岁差矩阵，NR为章动矩阵，ER为地球自转矩阵，EP为极移矩阵，EDR为地球自转矩阵的导数矩阵。

2) 将地固系位置速度转到测站东北天坐标系下，由测站大地坐标可计算出地固系到测站东北天坐标系的转换矩阵MES，则有

ρS=MES(rE-RS)

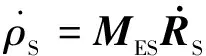
(18)

这样，即可计算出外弹道测量的4个观测量：

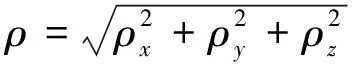
A=arctan(ρx/ρy)

(19)

滤波中对外弹道测量数据的使用，即观测方程的建立过程，主要有两种方法，一种是直接使用测距与测角转换出的位置数据；另一种是直接将观测方程建立在测站东北天坐标系中[7-8]。

考虑到上面级飞行高度较高，较小的测角误差就会产生较大的位置偏差；并且各测元之间测量精度差异较大。为此本文观测方程的建立采用后一种计算方法。

2.2 轨道机动过程弹道计算

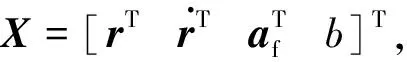
(20)

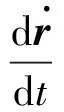
对k时刻到k+1时刻的系统状态外推预测可通过对上述动力学模型进行Runge-Kutta积分得到。

2.3 机动过程Q矩阵自适应处理

火箭及上面级飞行过程存在多次机动运动，且各次机动的加速度存在较大差异。这给弹道重建带来了较大困难。对αβ模型，若将Q矩阵设置为恒定值，则机动发生时，若未能根据当前推力情况对af进行精确建模，并使外推模型及时切换到有推力作用的状态，则滤波状态更新将与实际情况出现较大偏差。从而导致滤波计算需要很长时间进行状态调整，极大降低收敛速度。为此，需要在机动发生时及时调整滤波状态参数。一种方法是实时接收火箭遥测判定的机动特征点，在特征点处对滤波P矩阵及模型中加速度按当前推力、比冲、火箭飞行姿态等参数计算初始化值。但这种方法应用于多次机动时显得比较麻烦，特别是对姿态数据的引入。

考虑到机动发生时，火箭及上面级飞行的加速度变化趋势会发生突变。此时，若滤波状态外推未能及时反映出此变化，则原状态外推模型中的状态协方差矩阵Q将与当前系统真实状态出现较大偏差，为此可通过对Q矩阵进行实时调整的方法来使得滤波计算实现对机动过程的自适应处理。

(21)

(22)

考虑到机动发生时，滤波状态变量X中加速度迅速改变，而加速度的改变会影响速度与位置的改变。为此，可参照式(22)来调整Q矩阵中加速度分量。对αβ模型，其加速度包括机动推力加速度、三体引力加速度、大气阻力加速度等，考虑到轨道机动过程中，推力加速度占主要地位，其他加速度为小量。为此可直接使用式(22)进行加速度增量的近似计算。

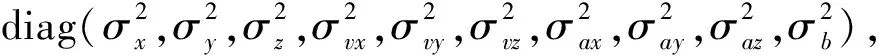
设k-1时刻到k时刻的时间增量为T，并在计算公式中引入调整系数λ，合理设置λ以增强自适应能力。从而可将Q矩阵中加速度x,y,z方向分量的方差分别自适应调整为位置与速度的函数：

(23)

式中，i=0,1,2表示x,y,z各方向分量。

实际计算中，若只对Q矩阵加速度方向进行调整，将使得震荡加剧。为此，还需对速度方向进行限制性调整。计算公式为

(24)

对位置方向，可将其方差置为固定值。对b分量，在火箭基础级飞行段，机动加速度大，可将其置为一非零固定值(如10-10)；对上面级，推力加速度稍小，可置为一更小的值或0。

3 仿真及实测数据计算

算例1：以某颗导航星发射过程中基础级及上面级飞行为例进行仿真计算。针对基础级及上面级分别作两段数据的仿真：

1) 基础级飞行段，包括了一、二、三级飞行及基础级与上面级分离等阶段；

2) 上面级后期飞行仿真，包括第二滑行段、第二主动段、末修段、调姿段、卫星分离等阶段。

基础级仿真为多站仿真，仿真时以某星发射的理论飞行弹道为依据，同一跟踪区间设置双站跟踪(跟踪值计算方法为根据测站坐标将理论弹道转换为东北天坐标系下的测量值)，并对测距、方位角、仰角、测速仿真数据分别加上20 m，0.01°，0.01°，0.1 m/s的随机噪声(1σ)。此时滤波计算的飞行速度(v)、速度与地面夹角(θ)曲线如图1所示，横轴为相对起飞时刻的时间(t)。

(a)基础级滤波速度曲线

对上面级飞行采用单站仿真，各测量量所加随机差同基础级。此时滤波计算的飞行速度(v)、速度与地面夹角(θ)曲线如图2所示。

(b)速度地面夹角曲线图2上面级滤波曲线

从图1、图2可以看出，滤波对基础级二级关机、三级关机点、上面级第二主动段点火点等均较好地实现了自适应处理。

算例2：使用某MEO卫星发射时基础级及上面级飞行过程实际跟踪测量数据进行算法有效性验证。

上面级在第二滑行段(1 600多秒至1万多秒)为慢旋飞行状态，导致地面外弹道测量设备跟踪不稳定，测量数据震荡较大，野值较多，给滤波适应能力带来较大挑战。

作为对比，同时采用3种计算方法进行计算。方法1：采用EKF算法，外推采用当前统计模型；方法2：采用UKF算法，计算时未进行方差矩阵自适应调整；为使结果曲线光滑，对基础级飞行段(1 200 s前)与上面级跟踪弧段设置不同的P矩阵初值，并给基础级滤波设定较大的遗忘因子不断放大P矩阵(未放大时此方法对基础级常常滤波发散)；方法3：采用本文算法，给定调整系数λ取值0.1。

此时几种滤波方法计算的实时飞行轨道的近地点高度(Hp，此值对精度较敏感)曲线如图3所示，横轴为相对起飞时刻的时间t。

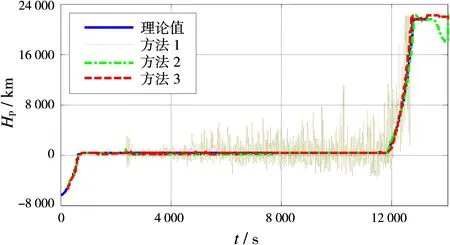
图3 某星实测数据滤波计算的Hp曲线

从图中看出，方法1对基础级较有效，但由于上面级观测数据质量太差，导致此方法计算结果质量也很差。原因在于此方法未进行动力学建模，抗野值能力较差[10]。

方法2与方法3结果质量明显好于方法1。但方法2在特征点附近适应性要差于方法3，且方法2对基础级与上面级分别设定了不同滤波参数，显得较为麻烦。

对于方法3，在上面级主发动机第二次点火点(约11 790 s)、第二主动段结束点(约12 700 s)，以及基础级三级关机等关键特征点处，滤波算法较好地实现了自适应跟踪。但由于上面级跟踪数据稳定性很差，对Hp曲线局部放大时会发现该曲线震荡仍较大，平滑性还有待进一步改进。

4 结束语

本文对中心差分卡尔曼滤波计算方法进行了阐述，给出了针对火箭机动飞行过程实时定轨计算的滤波状态外推模型和观测模型，以及一种基于位置速度计算的Q矩阵自适应处理方法。仿真及实测数据计算结果表明所给出的算法和模型是有效的。算法具有较好的稳定性、自适应能力和抗差能力。

应该看到，算法还有很多需要进一步改进或对性能影响较大的地方。如在Q矩阵自适应调整时，对调整系数等参数较为敏感，系数较大时，对机动反映及时，但结果震荡增大，故实际中需合理设置该值。下一步将重点在滤波模型及参数的进一步优化上进行研究。

[1] 林木. 运载火箭上面级功能与技术发展分析[J]. 上海航天, 2013, 30(3):33-38.

[2] 马昆,郭武,关嵩,等. 上面级发展现状及趋势分析[J]. 导弹与航天运载技术, 2013(6):24-28.

[3] NORGAARD M, POULSEN N K, RAVN O. New Developments in State Estimation for Nonlinear Systems[J]. Automatica, 2000, 36(11):1627-1638.

[4] 淡鹏,李恒年,张定波,等. 基于多元非完备信息的实时滤波定轨方法[J]. 飞行力学, 2014, 32(3):285-288.

[5] 刘伟,刘宁. 一种基于UKF交互多模型算法[J]. 雷达科学与技术, 2015, 13(3):302-304, 309.

LIU Wei, LIU Ning. A UKF Based Interactive Multi-Model Algorithm[J]. Radar Science and Technology, 2015, 13(3):302-304, 309.(in Chinese)

[6] ARASARATNAM I, HAYKIN S. Cubature Kalman Filters[J]. IEEE Trans on Automatic Control, 2009, 54(6):1254-1269.

[7] 淡鹏,李恒年,张智斌. 一种火箭外测弹道实时重建的自适应滤波算法[J]. 弹箭与制导学报, 2013, 33(6):186-188, 192.

[8] 淡鹏,李恒年,张定波. 多源观测数据融合星箭分离初轨计算[J]. 载人航天, 2015, 21(4):398-403.

[9] 李恒年,李济生,黄永宣. 有连续推力控制的卫星轨道确定算法[J]. 系统工程与电子技术, 2010, 32(9):1957-1961.

[10] 淡鹏,李恒年,李志军. 应用三向测量数据的深空探测器实时滤波定位算法[J]. 航天器工程, 2015, 24(2):21-26.

[11] 胡振涛,刘先省. 基于“当前”统计模型的一种改进机动目标跟踪算法[J]. 山东大学学报(工学版), 2005, 35(3):111-114.

[12] 隋红波,房晓颖,吴瑛. 改进的当前统计模型及自适应跟踪算法[J]. 雷达科学与技术, 2008, 6(3):202-205.

SUI Hongbo, FANG Xiaoying, WU Ying. A Modified Adaptive Tracking Algorithm Based on Current Statistic Model[J]. Radar Science and Technology, 2008, 6(3):202-205.(in Chinese)

[13] 金亮亮,刘亚云. 一种改进自适应机动目标跟踪算法[J]. 雷达科学与技术, 2014, 12(1):97-100.

JIN Liangliang, LIU Yayun. An Improved Tracking Algorithm for Maneuvering Target[J]. Radar Science and Technology, 2014, 12(1):97-100.(in Chinese)