基于GPU的RFT算法并行化

， ， ， ，

(1.空军预警学院研究生管理大队， 湖北武汉 430019；2.空军预警学院， 湖北武汉 430019)

0 引言

随着超高声速目标的涌现，给传统雷达检测带来巨大的挑战。现有的相参积累方式，如动目标检测(MTD)，是根据目标在相参积累时间内运动不超出一个距离单元来进行设计的，因此相参积累提升效果被限制在一个距离单元内。所以，在相参积累时间内“跨距离单元”和“多普勒模糊”将严重影响能量积累效果。许稼等[1-2]将Radon-Fourier变换(RFT)引入雷达信号处理当中，RFT是一种广义的MTD，通过提取目标速度-距离二维信息，利用离散傅里叶变换(DFT)，沿着提取的目标运动轨迹进行相参积累。

但是，由于RFT的巨大运算量使得很难满足实时性要求和工程化实现。为了解决这一问题，文献[3-4]提出基于Chirp-Z变换的快速RFT算法(CZT-RFT)。虽然快速RFT算法在一定程度上减少了运算复杂度，但是随着对模糊数搜索的增加运算量依然巨大[5]，难以满足实时性要求。文献[6]提出使用粒子群优化算法(PSO)对参数空间进行搜索，但是PSO对初值设置敏感，运算速度不稳定。近年来，图形处理单元(Graphic Process Unit, GPU)在并行运算方面显现出巨大优势，基于GPU的通用计算越来越受到国内外学者的关注，在雷达信号处理方面相关运用的文献也层出不穷。文献[7-8]分别讨论了软件雷达信号处理的单GPU实现和多GPU实现技术。文献[9]详细讨论了基于GPU平台的多元静态雷达(Parasitic Multistatic Radar)信号处理流程。文献[10-11]基于GPU平台加速了合成孔径雷达(SAR)成像算法。因此，针对RFT算法计算量大的问题，本文研究了基于CPU-GPU异构系统下的RFT算法并行化实现，以提高RFT的执行效率。通过对RFT算法的分析设计出RFT算法的“线程-线程块-网格”三级分配策略，通过仿真分析证明了并行化RFT可以得到可观的加速比，加速比随基积累时间的增加成线性增加，最大可达到2 200倍的加速比。同时分析了基于GPU的RFT算法(GPU-RFT)与基于CPU的MTD(CPU-MTD)的时间消耗，指出在运算速度上GPU-RFT快于CPU-MTD，但由于从设备端到主机端的传输带宽限制，使得GPU-RFT整体执行时间大于CPU-MTD。

1 RFT算法

假设雷达发射线性调频信号(LFM)，则目标回波经过脉压后为

(1)

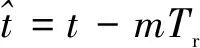
根据式(1)sinc函数的性质可知，由于目标的高速运动使得目标回波脉压后的峰值出现距离移动，同时由于速度多普勒大于脉冲重复周期，出现速度模糊。通过RFT算法可以同时解决这两个问题，标准RFT算法在时域进行，根据目标的初始位置和速度R0+vrmTr/ρs(ρs=c/2fs为采样单元)，提取目标回波脉压后的二维信息，同时利用DFT对固定频点fd=2vr/λ进行积分实现相参积累。因此， RFT算法的离散形式可写为

(2)

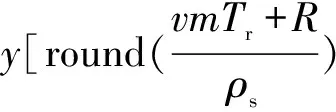
2 RFT算法并行化

为了充分利用GPU的并行性来提高执行效率，“线程-线程块-网格”三级线程并行化策略要充分根据RFT算法进行设计。RFT算法整体流程如图1所示。

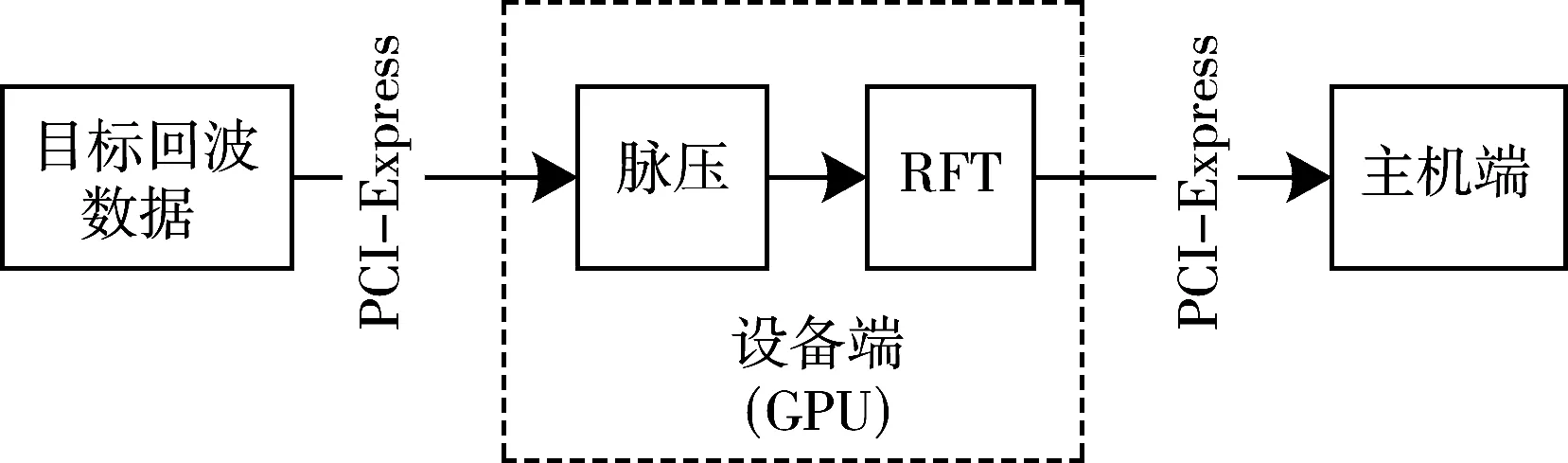
图1 RFT算法流程

目标回波数据直接由主机端送入设备端，在GPU内实现脉压和RFT算法，脉压的GPU实现文献[7-8]已作了详细的分析，本文主要关注RFT算法的GPU实现，如图2所示。假设雷达回波数据为L×M的双精度浮点复数，L为采样单元个数，M为脉冲积累数。RFT算法速度搜索数为N，速度分辨率与MTD相同为Δv=λ/(2MTr)。

根据图2，每个线程根据其所在线程块内和网格内的坐标，分配计算一组(R,v)的RFT结果，在线程内通过DFT实现相参积累。具体计算方式如下：

初始距离单元：

R=tx

(3)

式中，tx为线程块内线程x方向索引值。

搜索速度值：

v=[ty+(bx+by·Dbx)Dty]Δv

(4)

式中，ty为线程块内线程y方向索引值，bx为网格内线程块x方向索引值，by为网格内线程块y方向索引值，Dbx为设置的网格内线程块x方向最大索引值，Dty为设置的线程块内线程y方向最大索引值， Δv=λ/(2MTr)为速度搜索步进，将式(3)和式(4)代入式(2)在线程中计算RFT结果，即

(5)

图2 GPU-RFT算法并行化策略

在每一线程内，通过DFT即式(5)计算一组(R,v)的RFT结果。

由于单个Block中最大线程数[12]的限制(Max Thread Per Block, MTPB)，所以要满足：

Dty·Dtx≤MTPB

(6)

式中，Dtx为设置的线程x方向最大索引值。

因此，每个线程块内可搜索的速度个数为

Dty=MTPB/L=n

(7)

设置线程块x方向最大索引值为Dbx，使得Dty和Dbx满足：

Dty·Dbx=M

(8)

即线程块的每一行(x方向)，搜索与MTD相同的速度个数。设置需要搜索补偿的最大模糊数[3]为P，速度搜索数满足：

Dty·Dbx·Dby=M·P=N

(9)

式中，N为离散化速度搜索个数。通过上述并行化策略，可以让RFT算法在拥有与MTD相同的速度分辨率的情况下，速度的搜索范围达到MTD的P倍。

3 仿真分析

本文使用C语言和CUDA来实现RFT算法在GPU上的并行化，算法使用CPU-GPU异构平台，CPU为Intel i7-3770, GPU为Nvidia GeForce GTX 650，MTPB=1 024。雷达系统参数为：载频fc=1 GHz，带宽B=4 MHz，脉冲宽度Tp=128 μs，采样频率fs=4 MHz，脉冲重复频率fp=500 Hz。动目标参数为：初始距离R01=76 km，R02=74 km，R03=70 km，径向速度vr1=300 m/s，vr2=1 200 m/s≈3.5 Ma，vr3=-2 000 m/s≈-5.9 Ma。并行化参数为：线程块内线程x方向最大索引值Dtx=512，线程块内线程y方向最大索引值Dty=n=2，网格内线程块x方向最大索引值Dbx=M/2，网格内线程块y方向最大索引值Dby=P/M/2=MP/2。脉压结果如图3所示，MTD积累结果如图4所示，RFT积累结果如图5所示。

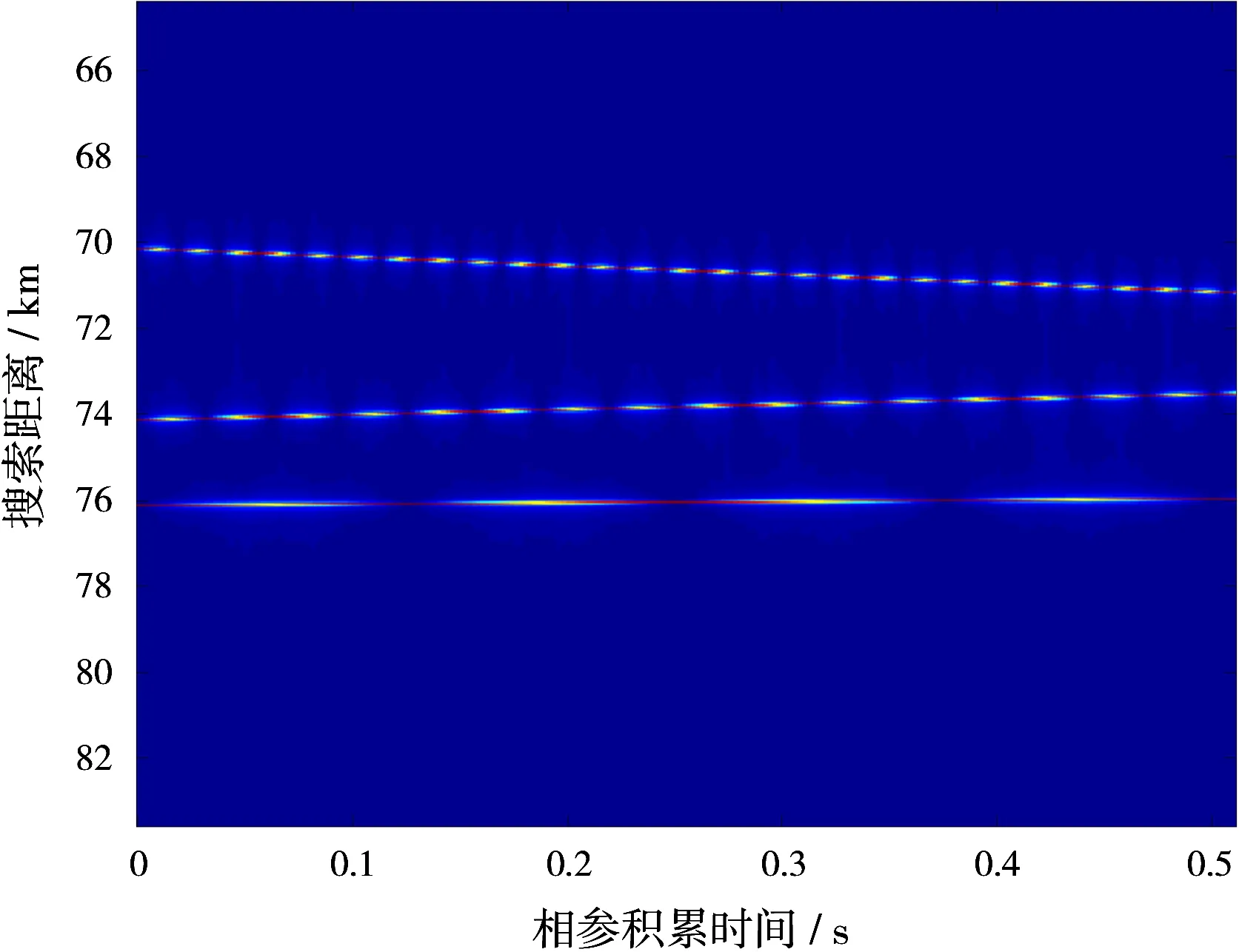
图3 脉冲压缩结果

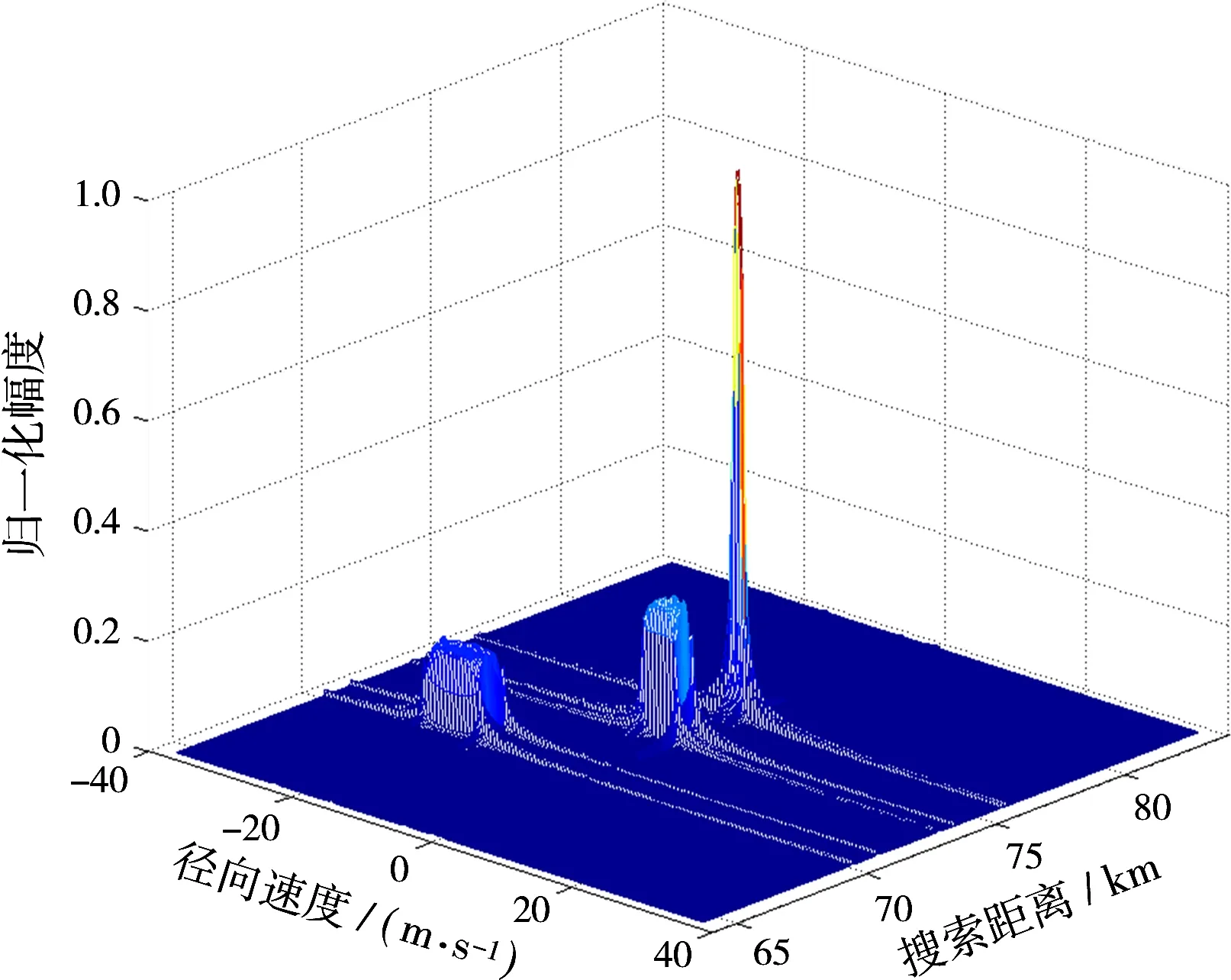
图4 MTD积累结果

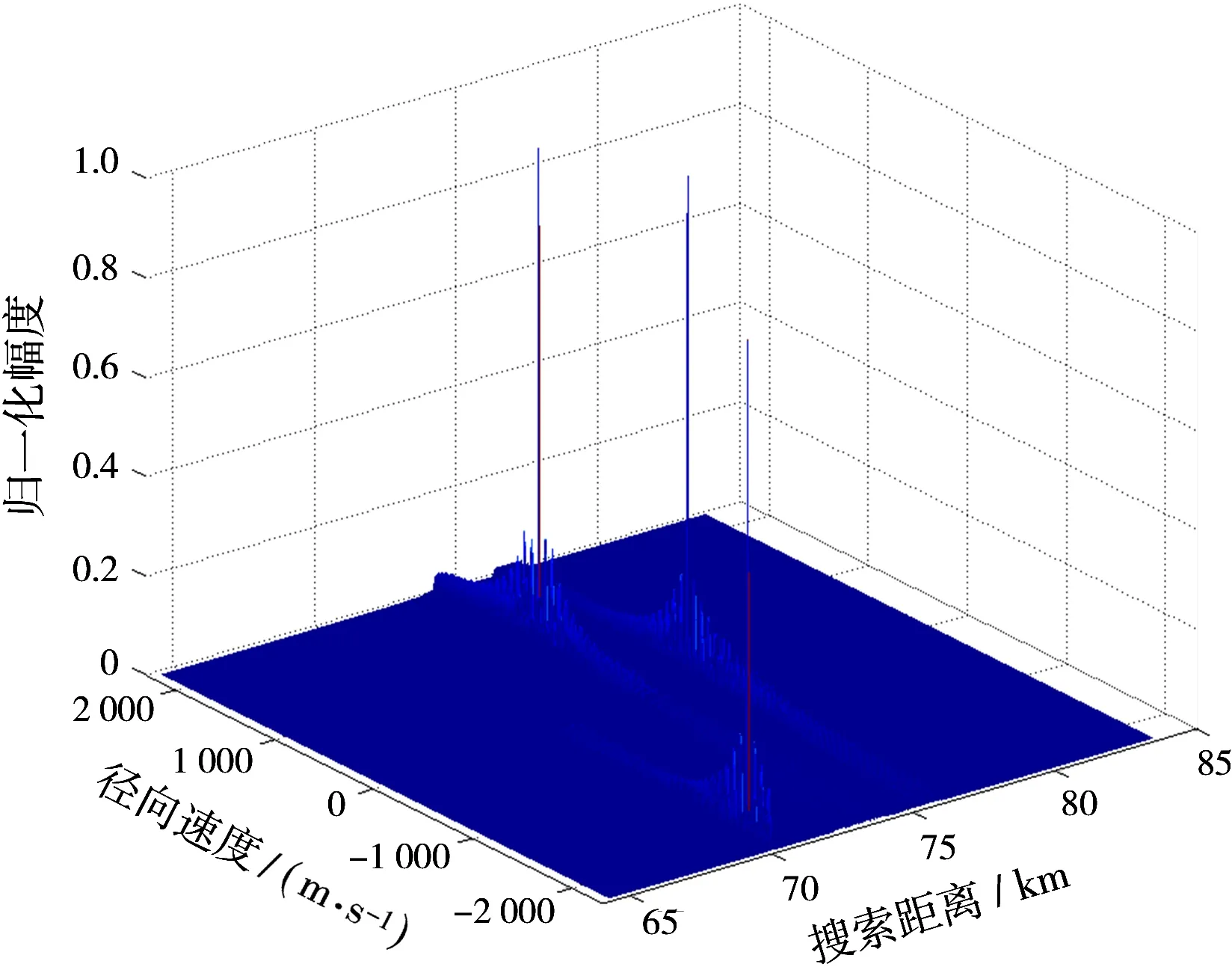
图5 RFT积累结果

脉压和RFT在GPU上的平均执行时间，以及与串行的执行时间对比如表1所示。

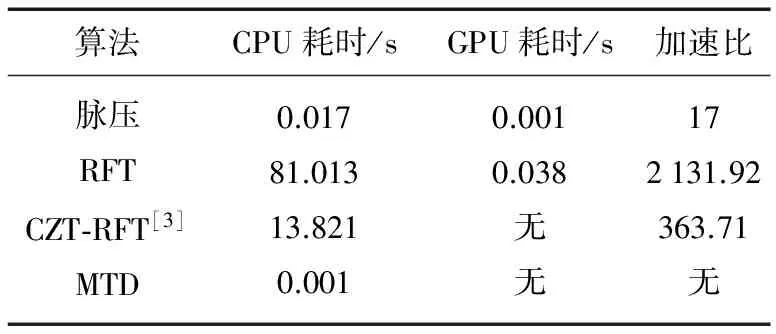
表1 算法并行和串行执行时间对比

表1中的RFT执行时间包括在GPU上的计算时间和将RFT结果数据由设备端传输到主机端的传输时间。通过表1可知，在GPU上执行RFT可以获得巨大的加速比，即使与快速RFT即CZT-RFT相比，GPU-RFT依然有巨大的速度优势。图6(a)显示了相参积累时间Tc=0.512 s时，加速比随速度搜索范围的变化规律；图6(b)显示了速度搜索范围为[-2 250 m/s， 2 250 m/s]时，随相参积累时间(脉冲积累数)加速比的变化规律。

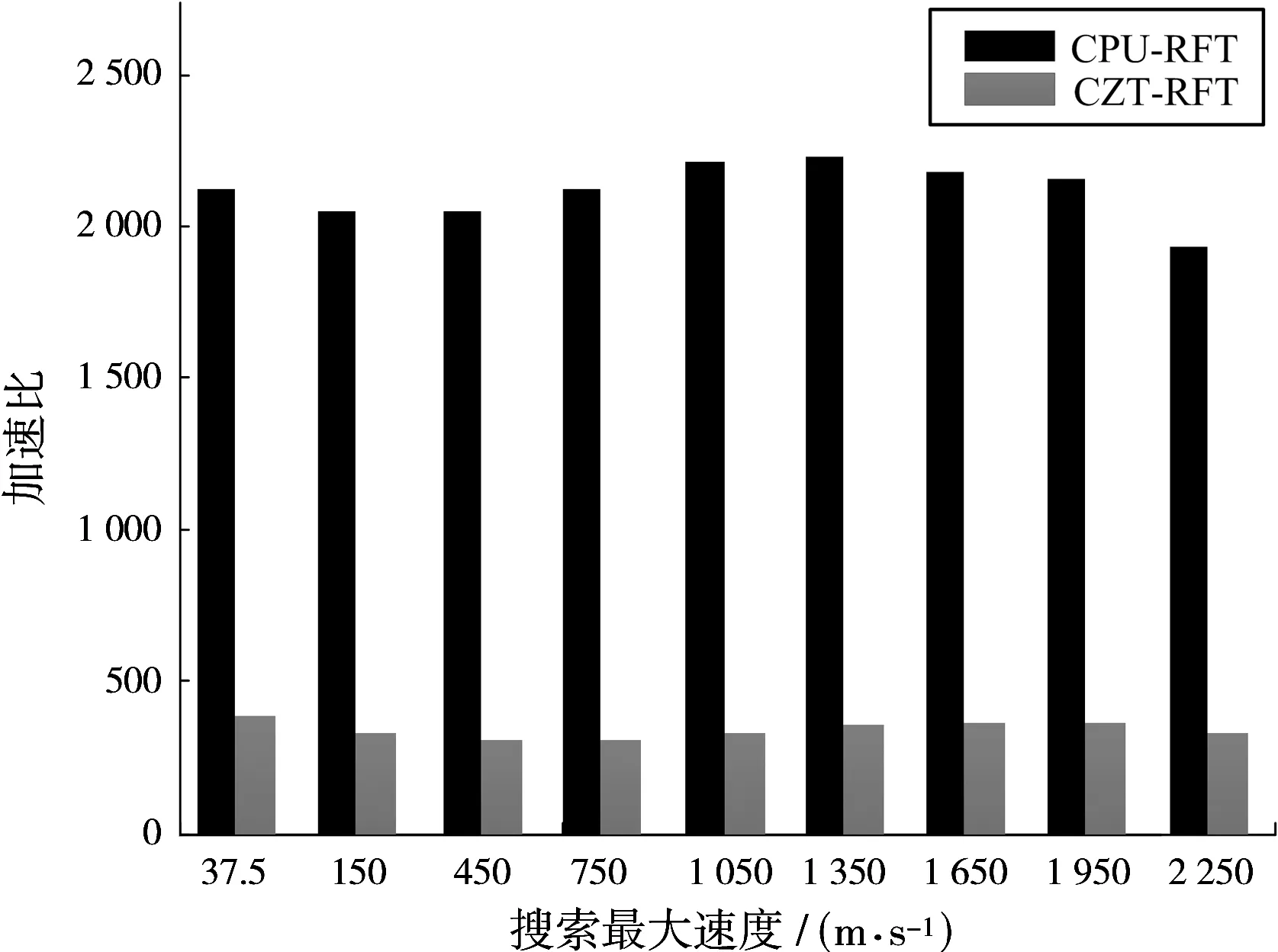
(a)加速比和速度搜索范围的关系

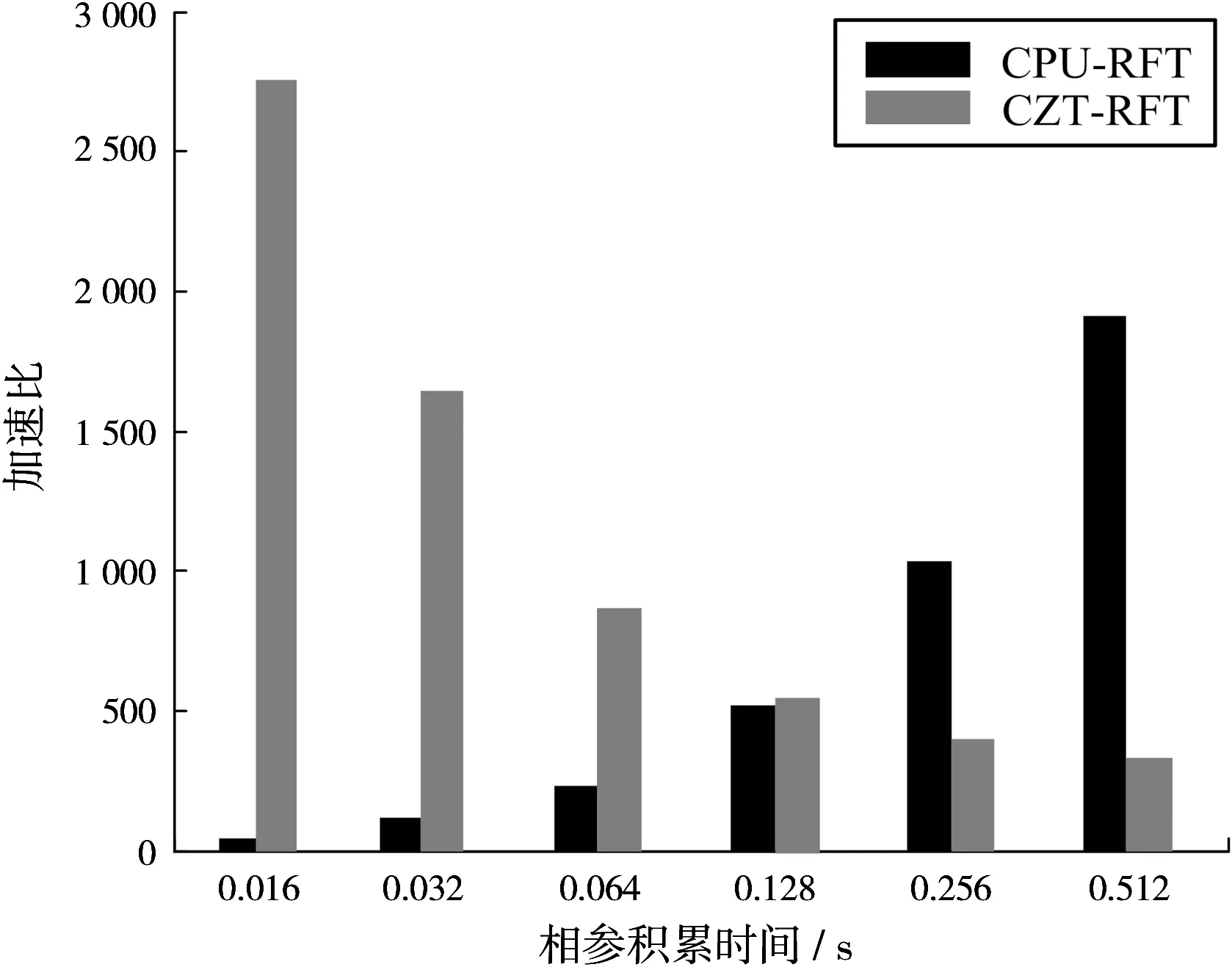
(b)加速比和相参积累时间的关系图6RFT在不同条件下的加速比

图6为基于CPU的RFT及CZT-RFT算法的执行时间与基于GPU的RFT算法执行时间之比获得的加速比，在不同条件下基于GPU的RFT算法均可获得巨大的加速比。事实上，不管是改变速度搜索范围还是改变相参积累时间，RFT在GPU上的计算耗时基本保持稳定，主要的时间消耗在数据传输上。例如，当速度搜索范围为[-2 250 m/s， 2 250 m/s]共N=15 616个速度搜索值，距离搜索范围为[64 km， 84 km]共L=512个距离单元，相参积累时间为0.512 s积累脉冲数M=256，每个搜索参数下的RFT结果为双精度复数大小为16 B，所以RFT结果产生的数据量为15 616×512×256×16/1 024/1 024=122 MB总线采用PCI-E 3.0实际传输带宽约为3.2 GB/s，传输时间约为37 ms，随着数据量的增加其耗时成线性增加。图7、图8分别为固定了速度搜索范围和距离搜索范围，随积累时间增加即处理的回波数据量的增加，GPU-RFT结果传输时间，以及GPU-RFT与CPU-MTD计算时间的变化规律。

图7 GPU-RFT结果传输时间

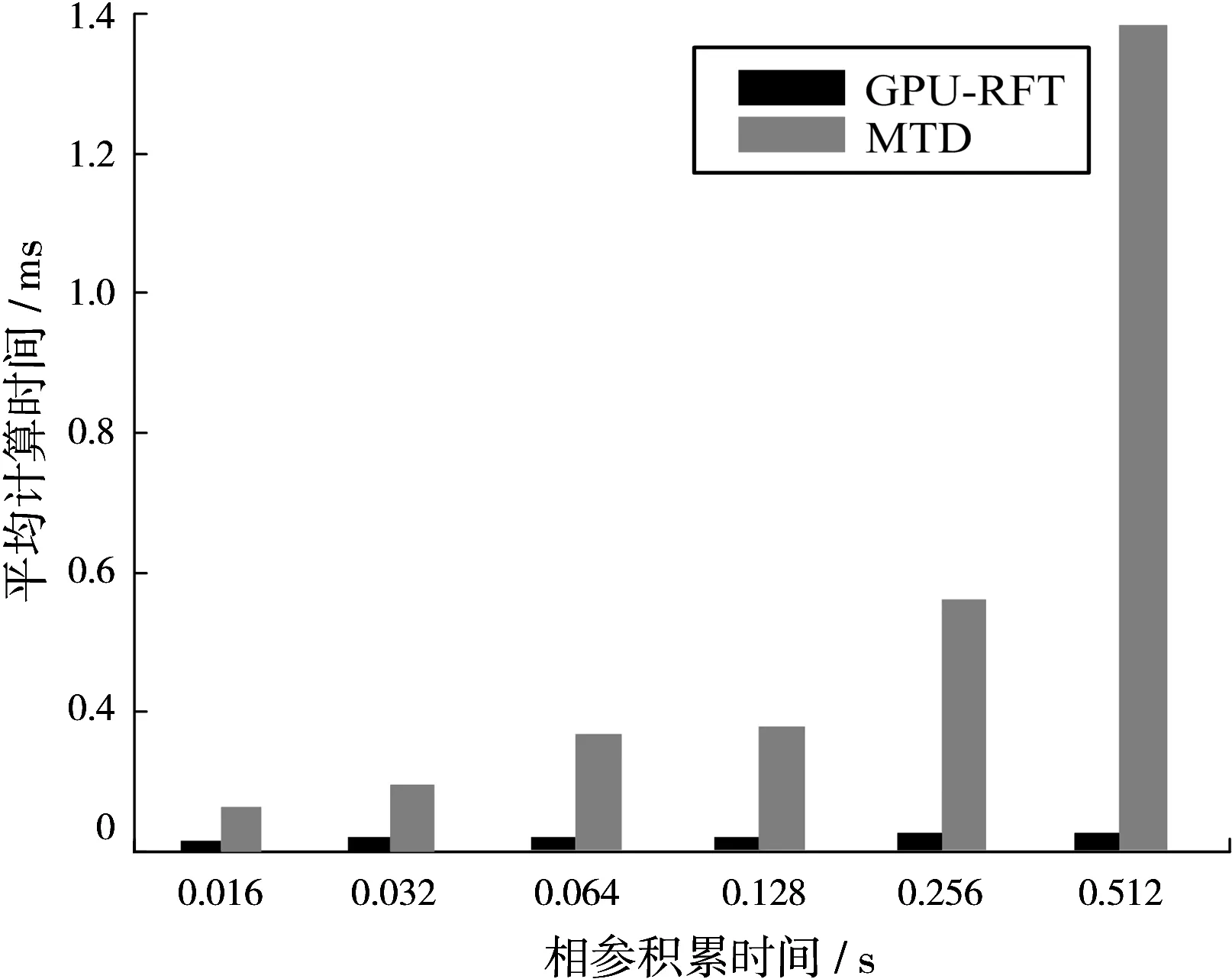
图8 RFT和MTD计算时间

综合图7和图8可知，从计算耗时上分析，GPU-RFT耗时也远远小于CPU-MTD，且由于并行执行，所以回波数据量的增加并没有对GPU计算时间带来显著的影响。但由于回波数据量的增加导致RFT结果数据量增加，传输时间增加，最终导致其执行时间大于CPU-MTD。

4 结束语

RFT算法是一种广义的MTD算法，可以沿着目标运动轨迹实现相参积累。但是由于巨大的计算压力，RFT很难进行工程化。基于GPU的RFT算法让RFT算法获得了巨大的加速比，使其工程化成为可能。通过对CPU执行的MTD与基于GPU的RFT算法比较发现，RFT在GPU上的计算时间小于CPU上计算MTD的时间，但由于带宽限制，RFT结果数据从设备端传送到主机端的时间过长，使得基于GPU的RFT算法总体执行时间长于MTD。

[1] XU Jia, YU Ji, PENG Yingning, et al. Radon-Fourier Transform for Radar Target Detection(I):Generalized Doppler Filter Bank[J]. IEEE Trans on Aerospace and Electronic Systems, 2011, 47(2):1183-1202.

[2] XU Jia, YU Ji, PENG Yingning, et al. Radon-Fourier Transform for Radar Target Detection(II):Blind Speed Sidelobe Suppression[J]. IEEE Trans on Aerospace and Electronic Systems, 2011, 47(4):2473-2489.

[3] 吴兆平,符渭波,郑纪彬,等. 基于快速Radon-Fourier变换的雷达高速目标检测[J]. 电子与信息学报, 2012, 34(8):1866-1871.

[4] YU Ji, XU Jia, PENG Yingning, et al. Radon-Fourier Transform for Radar Target Detection(III):Optimality and Fast Implementations[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(2):991-1004.

[5] 商哲然,谭贤四,曲智国,等. 基于改进的快速RFT算法的高速目标检测[J]. 雷达科学与技术, 2016, 14(2):184-188.

[6] QIAN Lichang, XU Jia, SUN Wenfeng, et al. Efficient Approach of Generalized RFT Based on PSO[C]∥IEEE 12th International Conference on

Computer and Information Technology, Chengdu:IEEE, 2013:511-516.

[7] 秦华,周沫,察豪,等. 基于GPU加速的雷达信号处理并行技术[J]. 舰船科学技术, 2013, 35(7):77-82.

[8] 秦华,周沫,察豪,等. 软件雷达信号处理的多GPU并行技术[J]. 西安电子科技大学学报(自然科学版), 2013, 40(3):145-151.

[9] JOHN M. Acceleration of Parasitic Multistatic Radar System Using GPGPU[D]. Cape Town:University of Cape Town, 2011.

[10] 孟大地,胡玉新,丁赤飚. 一种基于GPU的SAR高效成像处理算法[J]. 雷达学报, 2013,2(2):210-217.

[11] 姜晓龙,王建,宋千,等. 基于GPU的后向投影SAR成像算法[J]. 雷达科学与技术, 2014, 12(4):350-357.

[12] COOK S. CUDA C Programming Guide[M]. San Francisco, CA:Morgan Kaufmann, 2013.