基于多延迟相关参数的信号处理算法
2016-03-13,,2,,
, ,2, ,
(1.解放军理工大学气象海洋学院, 江苏南京 211101;2.南京气象雷达开放实验室, 江苏南京 210008)
0 引言
天气雷达是大气探测的重要工具之一,其回波数据是进行灾害性天气预警和短时天气预报的重要参考资料[1]。但是雷达回波信号中总是掺杂有部分噪声干扰信号,有时在回波信噪比较低的情况下,噪声信号甚至会“淹没”有用的降水回波信号。这严重制约回波信号的谱矩估计质量,影响雷达输出回波数据的应用潜力[2]。因此,对天气雷达信号处理算法进行改进,以期消除噪声信号对估计得到的回波数据质量的影响,是天气雷达研究领域非常有意义的一件工作。
天气雷达信号处理发展过程中,曾出现过多种信号处理算法[3],包括快速傅里叶变换(FFT)算法、矢量相位变换(VPC)算法、标量相位变换(SPC)算法、脉冲对处理(PPP)算法等。但在天气雷达实际信号处理中,不仅要考虑处理得到的回波数据质量,另外为了保证天气雷达能够实时处理,还要兼顾所选信号处理算法的运算速度。因此,目前天气雷达信号处理器中脉冲对处理算法应用最为广泛。在实际应用过程中,在弱回波区域,脉冲对处理算法得到的速度谱宽数据经常会存在一些异常数据,这严重影响回波数据的正常使用[4]。因此,为提高天气雷达数据质量,本文对传统信号处理算法进行改进,引入多阶延迟自相关参数。
1 传统信号处理算法介绍
文中信号处理主要是指时域I/Q(即同相/正交)数据处理得到谱矩参数的过程,其中时域I/Q数据是目标回波信号中一组相关的时域采样脉冲序列,如式(1)所示:
sn=In+jQn,n= 1,2,3,…,N
(1)
式中,In和Qn分别表示I路和Q路信号,N表示采样脉冲的数量。
目前天气雷达信号处理器主要使用脉冲对处理(Pulse Pair Processing, PPP)算法,其主要是根据回波信号的自相关参数进行计算[5-6]。主要处理过程为:首先,对时域I/Q数据进行滤波,消除地物杂波信号;然后,根据滤波后的时域I/Q数据计算各自相关参数,如式(2)所示;最后,根据自相关参数计算回波谱矩参数,如式(3)所示:
(2)
(3)
式中,R(mTs)表示m阶自相关参数,Ts表示脉冲重复周期,N表示平均噪声功率, *表示复数的共轭。
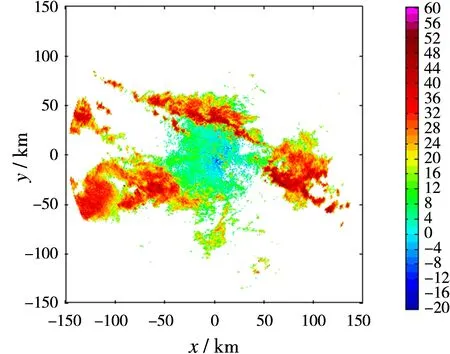
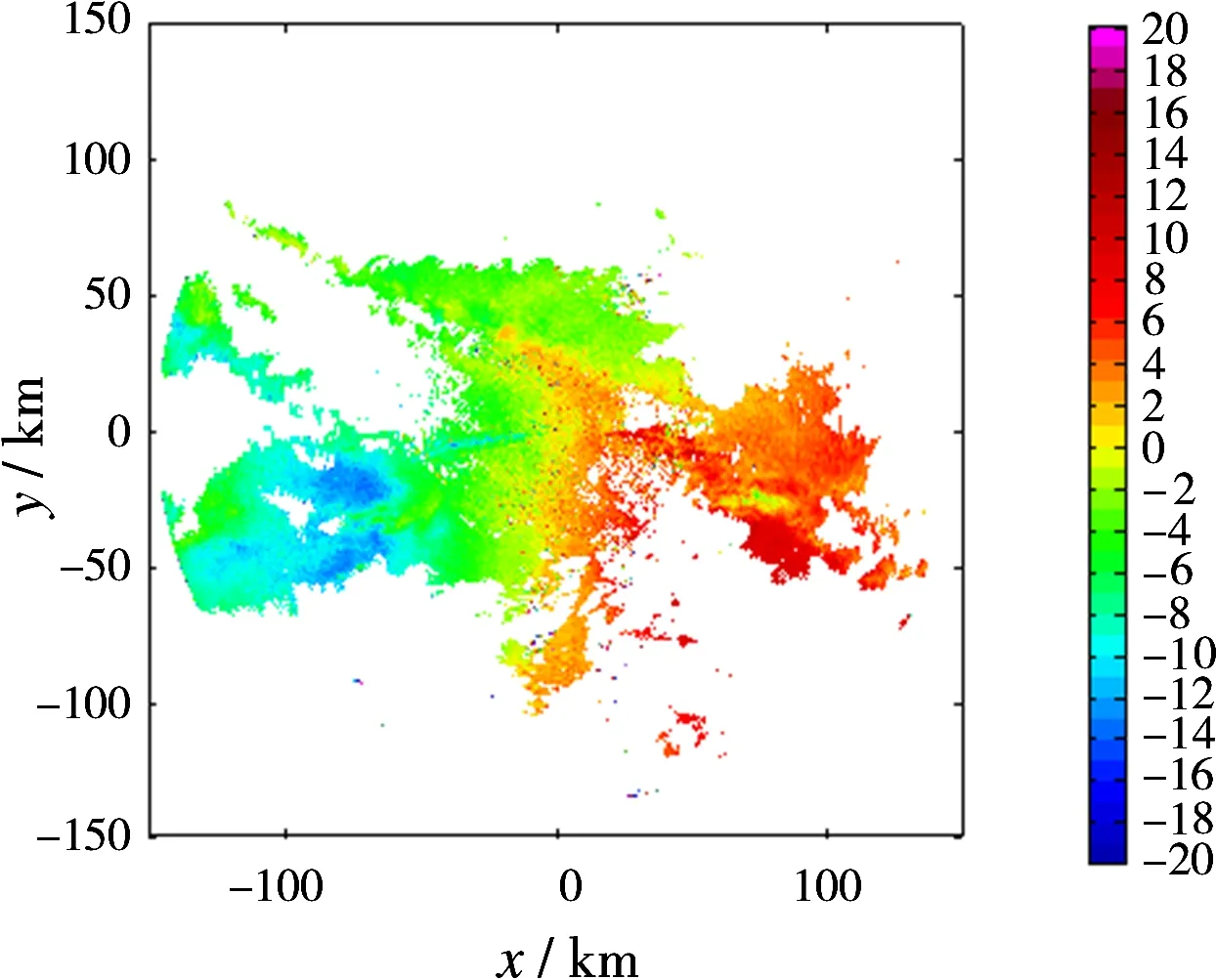
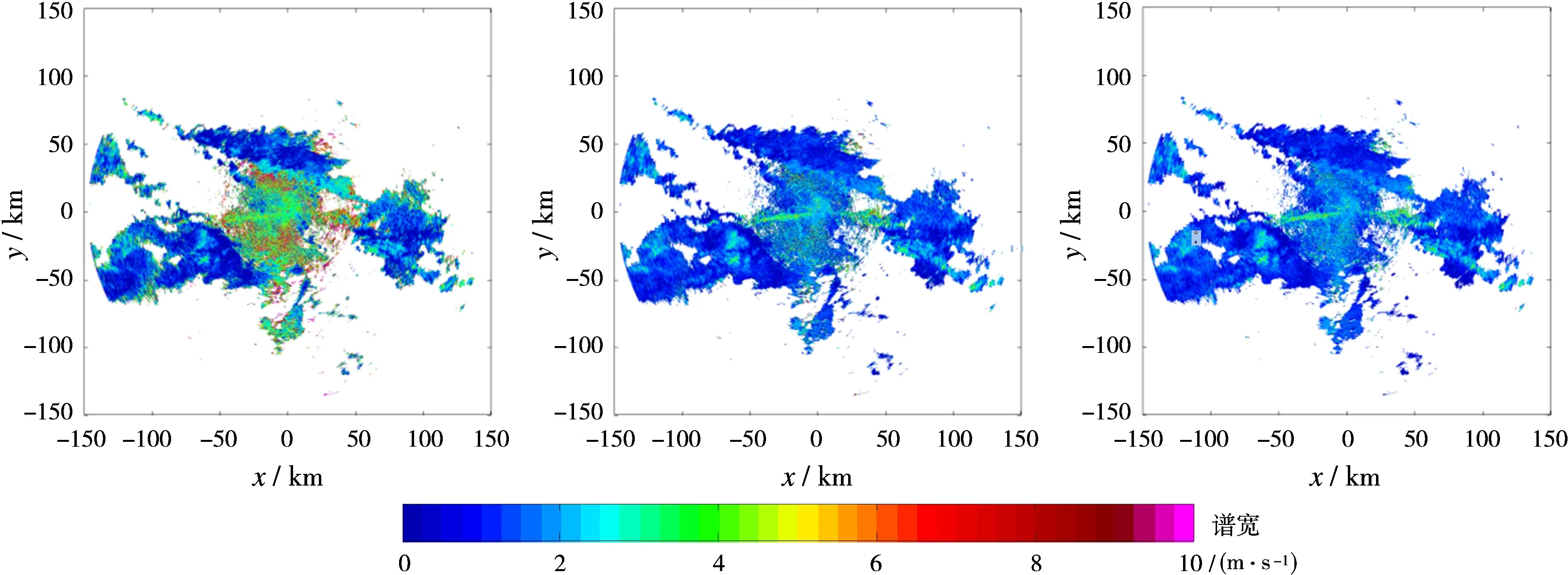
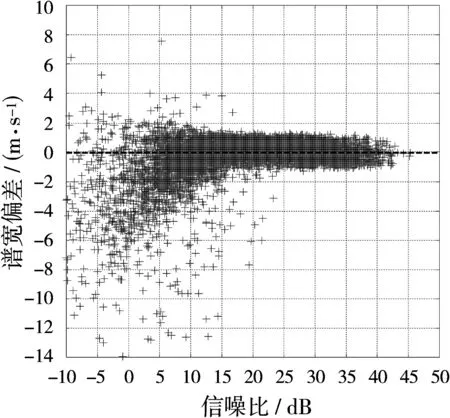
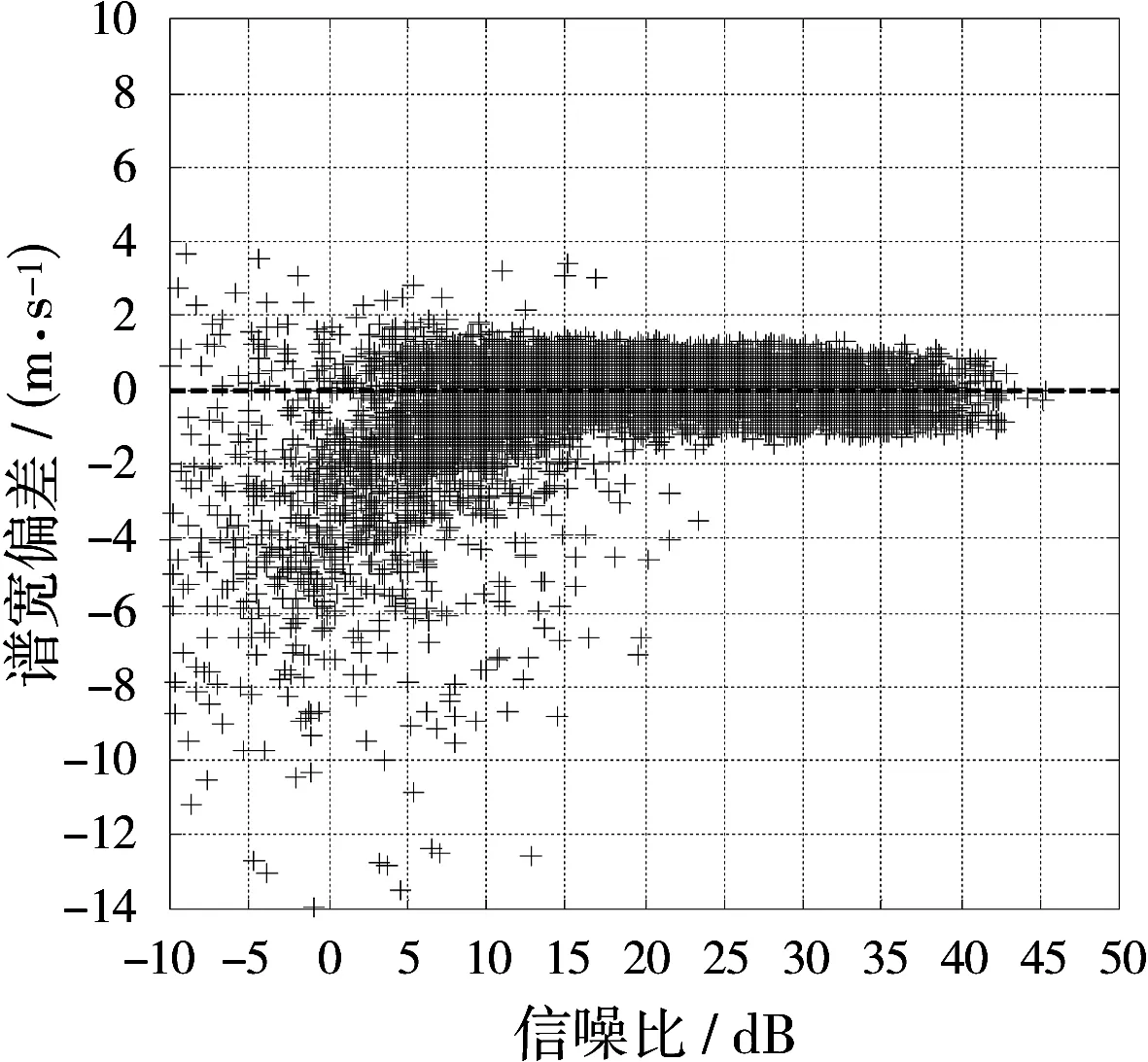
2013年,Ivic和Torres等对美国新一代天气雷达网中WSR-88D多普勒天气雷达平均噪声功率作了系统研究,结果表明,同一部雷达在正常工作情况下,不同时间、不同方位、不同仰角以及不同径向距离,其平均噪声功率通常存在较大差异,有时甚至超过2 dB[7-8]。然而,目前应用在业务观测中的天气雷达都是以较高仰角时晴空回波功率作为雷达平均噪声功率,应用该平均噪声功率输出的回波数据质量必将受到影响,尤其是回波信噪比较低的区域。当设置的平均噪声功率低于实际值时,速度谱宽估值偏大;反之,速度谱宽估值偏小,甚至会使得回波谱宽数据区域缩小(当R(0) Janssen和Spek采用5.56 GHz相控阵雷达对气象目标进行了长期观测,并对大量回波信号进行分析,研究结果表明:超过75%的回波信号功率谱都具有高斯形状[9]。因此,实际应用中通常将雷达接收的天气回波信号频谱近似为高斯分布,并用高斯函数表示天气回波信号功率谱S(v)[10]: (4) 由于功率谱S(f)与自相关函数R(l)互为傅里叶变换,因此,根据离散傅里叶变换(DFT)可以计算回波信号延迟mTs时相应的自相关参数R(mTs): (5) (6) 式中,Ts表示脉冲重复周期,mTs表示自相关函数延迟时间,δm表示冲击函数,当且仅当m为零时,自相关参数R(mTs)包含噪声分量。 根据式(6)可知,在脉冲重复周期Ts和雷达波长λ已知的前提下,只需要两个不同自相关参数就可以推导出速度谱宽σv的估计值。另外,为了消除传统信号处理算法中平均噪声功率对回波数据的影响,避免使用R(0)计算速度谱宽。又考虑到天气雷达回波脉冲样本较少,且脉冲相关性容易受延迟时间影响,因此,通常严格控制自相关函数的延迟时间,通常m≤3。本文提出Lag1&2算法(即使用一阶延迟自相关参数R(Ts)和二阶延迟自相关参数R(2Ts))和Lag1&3算法(即使用一阶延迟自相关参数R(Ts)和三阶延迟自相关参数R(3Ts))两种速度谱宽估计算法: (7) (8) 式中,σv2和σv3分别表示采用Lag1&2算法和Lag1&3算法得到的速度谱宽估计值,R(Ts),R(2Ts),R(3Ts)分别表示一阶、二阶、三阶延迟自相关参数。 本文将选取一次强降水过程的回波数据进行分析,比较传统信号处理算法与Lag1&2算法、Lag1&3算法得到的速度谱宽数据差异。由于是进行信号处理算法研究,实验中所有处理过程都是对时域I/Q数据进行处理。 图1(a)、(b)分别显示的是一次强降水过程回波反射率因子图像和回波平均径向速度图像。其中横纵坐标分别表示距离雷达站的径向距离,(0,0)位置表示雷达站所在位置。为滤除噪声回波,本文对参数估计得到的回波数据设置信噪比门限,即当回波信噪比(SNR)大于-10 dB时,输出该距离库回波数据。 图2(a)、(b)和(c)分别显示的是采用传统信号处理算法(如式(3)所示)、Lag1&2算法(如式(7)所示)、Lag1&3算法(如式(8)所示)处理得到的速度谱宽数据图像。比较上述图像,可以得出以下结论: 1) 在弱回波区域,采用传统信号处理算法得 到的速度谱宽数据更容易受噪声干扰,如图2(a)所示,在近雷达站区域以及降水回波边缘区域(由图1(a)可知,主要是回波强度较弱区域),其速度谱宽估计值明显大于图2(b)、(c),而且速度谱宽数据连续性较差; 2) 采用Lag1&2算法和Lag1&3算法得到的速度谱宽数据较为接近,但是在回波强度较弱的区域,Lag1&3算法得到的速度谱宽数据更加平滑,如图2(b)、(c)中近雷达站区域。 (a)反射率因子数据PPI图像 (b)径向速度数据PPI图像图1回波强度和速度数据图像 (a)传统算法 (b)Lag1&2算法(c)Lag1&3算法图2速度谱宽数据图像 为定量分析传统信号处理算法、Lag1&2算法、Lag1&3算法速度谱宽数据的差异,选取图2所示PPI图像中部分区域距离库数据进行分析。数据区间如下(共包含9 576个距离库的回波数据): 区域一,方位角240°~270°,径向距离60~90 km区间内速度谱宽数据; 区域二,方位角330°~360°,径向距离30~60 km区间内速度谱宽数据。 图3(a)、(b)和(c)分别显示的是Lag1&2算法与传统信号处理算法、Lag1&3算法与传统信号处理算法、Lag1&3算法与Lag1&2算法速度谱宽偏差随信噪比的分布图像。分析上述图像,可以得出以下结论: 1) 当回波信噪比小于5 dB时,与Lag1&2算法、Lag1&3算法相比,传统信号处理算法得到的速度谱宽数据普遍偏大,部分数据偏差甚至超过-10 dB; 2) 当回波信噪比大于10 dB时,Lag1&2算法、Lag1&3算法与传统算法速度谱宽偏差均匀分布在-1.5~+1.5 m/s区间内; 3) 当回波信噪比大于10 dB时,Lag1&2算法与Lag1&3算法得到速度谱宽数据基本一致,其偏差大都不超过±0.5 m/s; 4) 当回波信噪比小于5 dB时,Lag1&2算法与Lag1&3算法速度谱宽偏差分布范围变大。 (a)Lag1&2算法与传统算法 (b)Lag1&3算法与传统算法 当回波信噪比大于10 dB时,回波信号功率要远大于噪声功率,此时应用传统信号处理算法计算速度谱宽(即式(3)),噪声功率对计算结果的影响可以忽略不计。当回波信噪比小于5 dB时,回波信号功率接近甚至小于噪声功率,此时噪声功率对传统信号算法速度谱宽数据影响较大,由于设置的平均噪声功率偏低,导致传统信号处理算法速度谱宽数据偏大,而且随信噪比降低,噪声功率的影响愈加严重。另外,天气回波信号功率谱形状可能受回波信噪比影响,当回波信噪比小于5 dB时,回波信号功率谱与高斯函数偏差较大,导致Lag1&2算法与Lag1&3算法计算得到的速度谱宽数据存在一定误差,因此出现图3(c)中回波信噪比小于5 dB时谱宽偏差波动较大的现象。 (c)Lag1&3与Lag1&2算法图3速度谱宽偏差随信噪比分布图像(图中速度谱宽偏差分别指σv2 -σv、σv3-σv、σv3-σv2) 对传统信号处理算法计算速度谱宽式(3)进行分析,发现平均噪声功率是影响输出谱宽数据质量的一个不稳定因素,为了消除噪声功率的影响,就要避免使用零阶延迟自相关参数。因此,本文提出采用多阶延迟自相关参数进行计算,如采用一阶、二阶、三阶延迟自相关参数。由于该信号处理算法不涉及平均噪声功率,因此其可以提高低信噪比区域的回波数据质量。通过对传统信号处理算法、Lag1&2算法、Lag1&3算法输出的速度谱宽数据进行比较,发现:当信噪比小于5 dB时,传统信号处理算法输出的谱宽数据中掺杂有大量变化异常大的数值,而Lag1&2算法和Lag1&3算法输出的谱宽数据与真实情况更接近;另外,信噪比小于5 dB时,Lag1&2算法和Lag1&3算法输出的谱宽数据偏差波动较大,作者认为可能是由于低信噪比回波信号功率谱与高斯分布差异较大的原因。 天气雷达实际信号处理过程中需要考虑各种因素的影响,如回波信噪比、谱宽等因素,不同信号处理算法在不同条件下处理性能也是有差异的,接下来需要系统论证 Lag1&2算法和Lag1&3算法在不同条件下的处理性能。另外,后面将开展研究应用多阶延迟自相关参数算法改善偏振回波数据质量。 [1] 赵畅. 多普勒雷达及多源资料在局地短临预报中的应用[D]. 南京:南京信息工程大学, 2014. [2] FANG M, DOVIAK R J, MELNIKOV V. Spectrum Width Measured by WSR-88D:Error Sources and Statistics of Various Weather Phenomena[J]. Journal of Atmospheric and Oceanic Technology, 2004, 21(6):888-904. [3] SIRMANS D, BUMGARNER B. Numerical Comparison of Five Mean Frequency Estimators[J]. Journal of Applied Meteorology, 1975, 14(6):991-1003. [4] MONAKOV A, MONAKOV Y. Error Analysis of Pulse-Pair Estimates[J]. IEEE Trans on Aerospace and Electronic Systems, 2011, 47(3):2222-2230. [5] SKOLNIK M I. 雷达手册[M].3版. 南京电子技术研究所,译. 北京:电子工业出版社, 2010:781-784. [6] 卢小佳. 多普勒天气雷达信号处理的研究[D]. 合肥:安徽大学, 2014. [7] IVIC I R, CURTIS C, TORRES S M. Radial-Based Noise Power Estimation for Weather Radars[J]. Journal of Atmospheric and Oceanic Technology, 2013, 30(12):2737-2757. [8] IVIC I R. On the Use of a Radial-Based Noise Power Estimation Technique to Improve Estimates of the Correlation Coefficient on Dual-Polarization Weather Radars[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(9):1867-1880. [9] JASSEN L H, VAN DER SPEK G A. The Shape of Doppler Spectra from Precipitation[J]. IEEE Trans on Aerospace and Electronic Systems, 1985, 21(2):208-219. [10] TORRES S M. Estimation of Doppler and Polarimetric Variables for Weather Radars[D]. Norman, OK:University of Oklahoma, 2001. [11] 郗蕴天,陈春. 一种补偿低中频接收机I/Q不平衡的方法[J]. 雷达科学与技术, 2015, 13(6):604-608. XI Yuntian, CHEN Chun. A Compensation Method for I/Q Imbalance of Low-IF Receiver[J]. Radar Science and Technology, 2015, 13(6):604-608.(in Chinese)2 信号处理算法改进
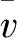
3 实测回波数据分析
3.1 回波数据选取
3.2 谱宽数据图像比较
3.3 谱宽散点数据分析
3.4 讨论

4 结束语
