异地配置的雷达与电子支援措施航迹关联

，

(海军航空工程学院电子信息工程系， 山东烟台 264001)

0 引言

雷达与ESM航迹关联是雷达与ESM数据融合的前提，是对目标进行更有效定位、跟踪和识别的必要条件。由于ESM属于被动传感器，仅有角度信息而没有距离信息[1-3]，且主被动传感器的数据率往往不一致，因而在雷达与ESM航迹关联中存在很多的困难与不确定性。根据传感器的相对位置不同，雷达与ESM航迹关联问题可以分为同地配置与异地配置两种情况[4]。同地配置的雷达与ESM航迹关联问题研究得较早且成果丰硕[5-12]。通常是在极坐标下利用角度量测构造统计量，然后根据相应的门限进行关联决策[5-7]。由于可利用的信息较少，所以需要较长的观测时间和观测样本才能达到较好的关联性能；或者对两传感器的量测进行滤波处理，根据不同的滤波方法，可用的关联向量也不同。通常运用滤波后的状态向量来进行航迹关联的性能比仅利用角度的方法好[7-12]，但是为了避免滤波器发散，要求被动传感器根据目标的运动情况进行一定的机动。

但是在实际应用中，会经常面临雷达与ESM异地配置的情况[13-16]。文献[15]提出了基于角度统计量和基于距离统计量的两种方法，仿真表明基于距离统计量的关联算法有相对较低的错误关联概率，但正确关联概率仍有待提高。本文首先利用雷达量测定义了ESM虚定位点；然后利用交叉定位点与ESM虚定位点来构造距离统计量，根据相应的门限进行关联判别；最后与文献[15]的基于距离统计量的方法进行了仿真对比，本文提出的方法取得了较好的关联效果。

1 ESM虚定位点

如图1所示，假设二维情况下两部异地配置的雷达和ESM在公共笛卡尔坐标系下同时对目标进行共同探测，其中雷达位于坐标(xa,ya)处， ESM位于(xb,yb)处。雷达在k时刻量测由距离和方位角共同组成，且该量测受到随机量测噪声影响，则

(1)

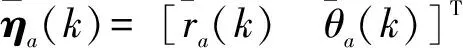
(2)

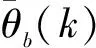
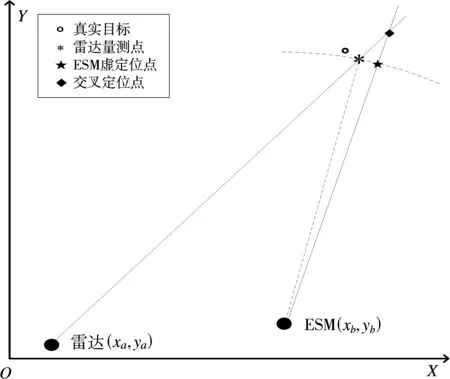
图1基于ESM虚定位点的雷达与ESM航迹关联示意图

图1中交叉定位点是由k时刻两个传感器测得角度交叉定位得到，其直角坐标为(x1(k),y1(k))：

(3)

定义ESM虚定位点，从几何图形直观描述为：以ESM为圆心，各雷达量测到ESM的距离为半径画圆，与ESM角度方向的交点为ESM虚定位点，其直角坐标为(x2(k),y2(k))，因此ESM关于目标的虚距离为

(4)

所以

(5)

式中，(xr(k),yr(k))是雷达关于目标的转换直角坐标：

(6)

2 基于ESM虚定位点的雷达与ESM航迹关联算法

2.1 构造关联统计量

k时刻交叉定位点到ESM虚定位点的距离为

d(k)=sgn(y1(k)-y2(k))·d12(k)

(7)

式中，

所以

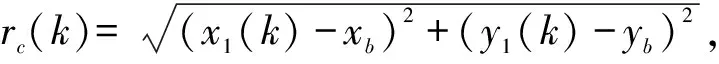
d(k)=rc(k)-rb(k)

(8)

从上式可以看出，d(k)是由ra(k),θa(k)和θb(k)确定，由于雷达的测距、测角和ESM的测角误差相互独立，服从高斯分布，所以式(8)可近似认为服从零均值的高斯分布，其方差为

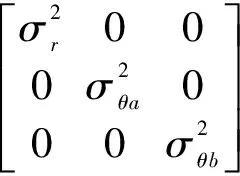
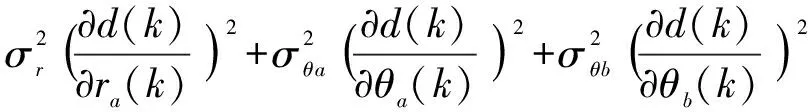
式中，

(10)

式中，各式中的偏导数如下:

(11)

(12)

(13)

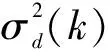
(14)

2.2 关联判决

得到基于距离统计量判别函数后，选择适当的关联决策门限η，雷达与ESM的航迹关联问题可以转化为如下假设检验问题：

H0：若Δ(n)>η，则判断雷达与ESM航迹不关联；

H1：若Δ(n)≤η，则判断雷达与ESM航迹关联。

当给定允许的漏关联概率为β时，决策门限η的选取应使得雷达和ESM在实际关联的情况下被错误判决为不关联的概率小于β，即Pr{H0|H1}≤α。当雷达和ESM航迹关联时，由式构造的距离统计量服从自由度为n的2分布。即

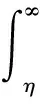
(15)

(16)

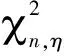
3 仿真分析

为了验证本文算法的有效性，用本文方法与文献[15]的基于距离统计量的方法关联性能进行仿真对比实验。仿真中， 正确关联概率为Ec=Nc/ (Nc+Ne+Ns)， 错误关联概率为Ee=Ne/ (Nc+Ne+Ns)，漏关联概率为Es=Ns/(Nc+Ne+Ns)，其中Nc,Ne和Ns分别为实验中正确关联、错误关联和漏关联点迹对的数目，且有Ec+Ee+Es=1。

实验1：不同雷达测角误差对算法的影响。假设雷达与ESM分别位于(0 km,0 km)和(100 km,0 km)， ESM的测角误差为0.6°，雷达测距和测角误差分别为1 000 m和0.1°～1.2°，允许的漏关联概率为0.1。以(40 km,70 km)与(60 km,90 km)为对角的矩形作为公共观测区域，随机产生10个直线运动目标，目标的初始速度和初始航向分别在50～70 m/s和0～2π内均匀分布。在上述条件下进行各100次蒙特卡洛仿真，图2和图3分别给出了不同雷达测角误差时雷达与ESM航迹正确和错误关联概率。

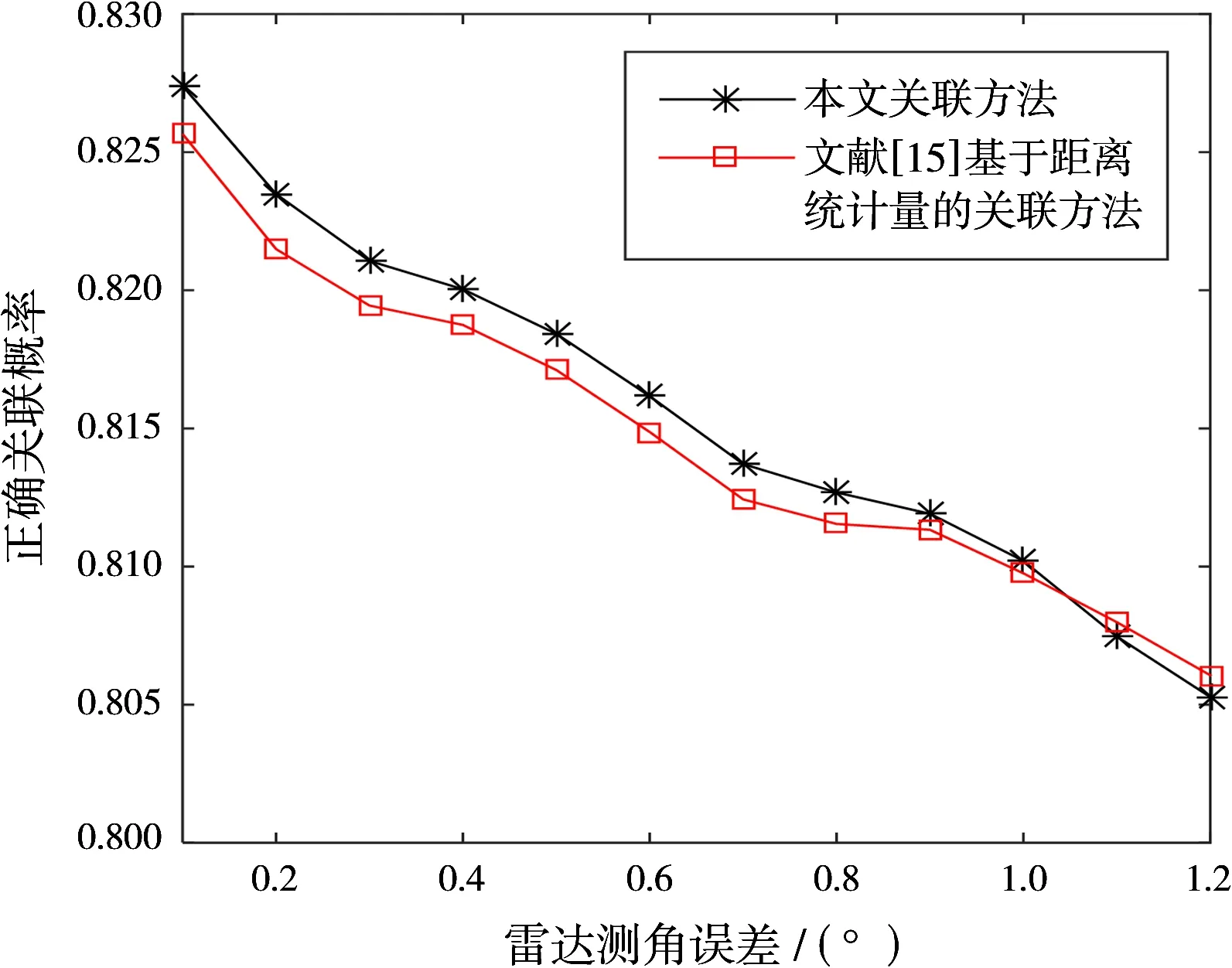
图2 不同雷达测角误差时雷达与ESM航迹正确关联概率

图3 不同雷达测角误差时雷达与ESM航迹错误关联概率

从图2可以看出，随着雷达测角误差的增大，两种方法的正确关联概率呈逐渐减小趋势，当雷达测角误差小于1.1°时，本文方法的正确关联概率优于文献[15]的关联算法。从图3可以看出，随着雷达测角误差的增大，两种方法的错误关联概率呈逐渐增大趋势，当雷达测角误差大于0.7°、小于1.1°时，由于文献[15]的关联算法具有较大的漏关联概率，导致其正确关联和错误关联概率均小于本文方法。

实验2：不同雷达测距误差对算法的影响。在其他条件同实验1完全相同的条件下，假设雷达测距误差为200～2 000 m，雷达测角误差为0.5°，分别进行100次蒙特卡洛仿真，图4和图5分别给出了不同雷达测距误差时雷达与ESM航迹正确和错误关联概率。

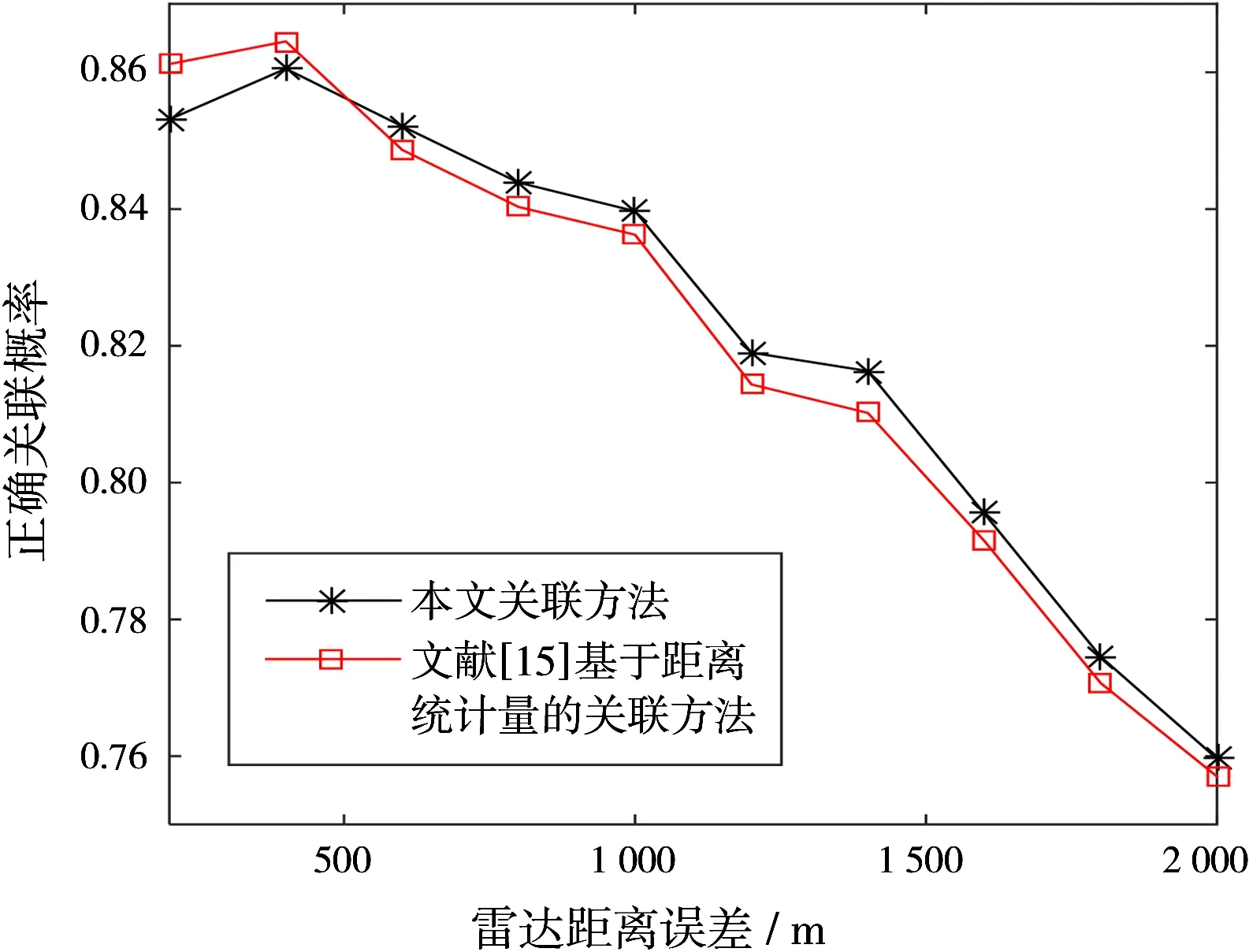
图4 不同雷达测距误差时雷达与ESM航迹正确关联概率

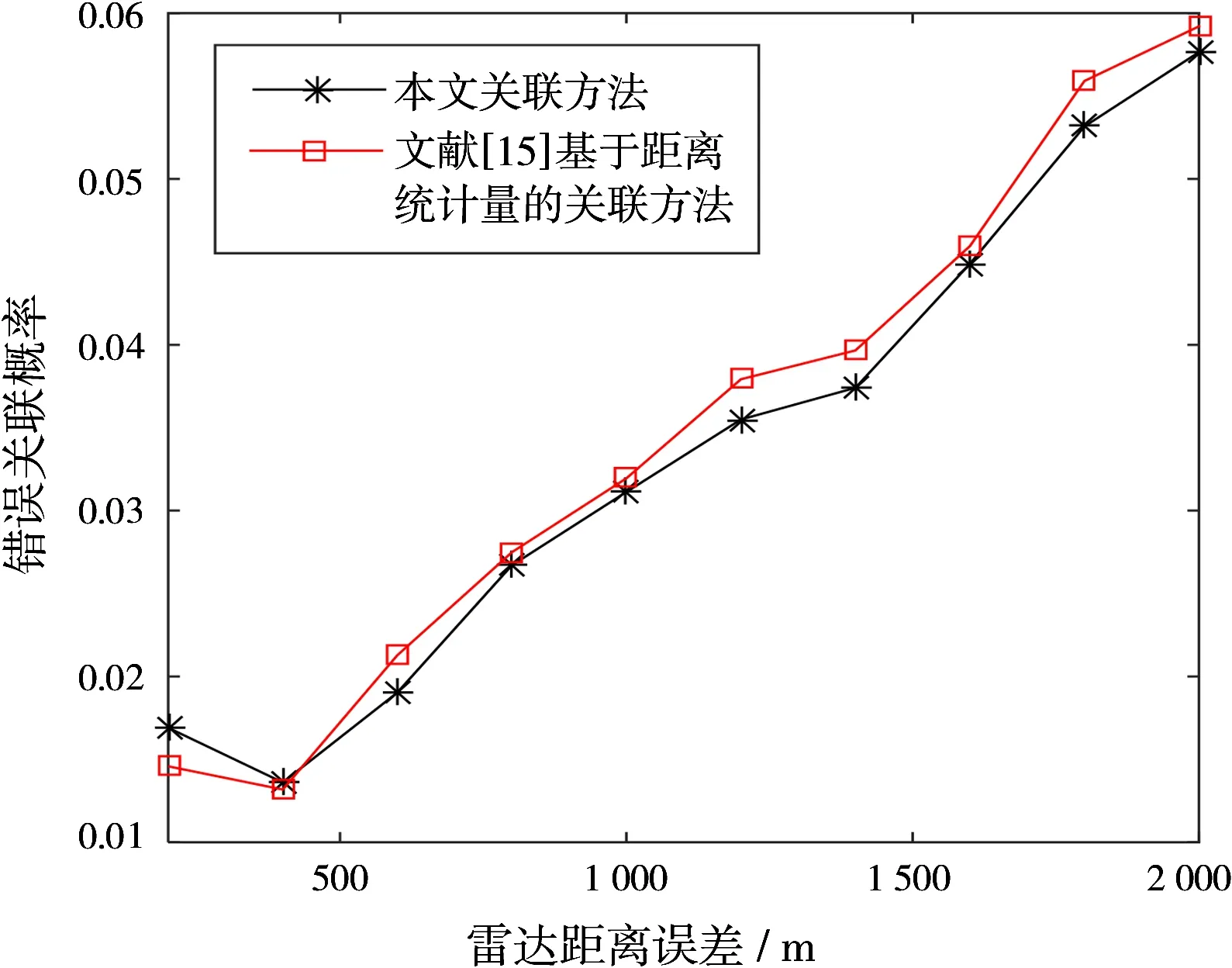
图5 不同雷达测距误差时雷达与ESM航迹错误关联概率

从图4可以看出，随着雷达测距误差的增大，两种方法的正确关联概率呈逐渐减小趋势，当雷达测距误差较小时，现有方法的正确关联概率大于本文的关联方法，但是当其大于600 m时，本文的关联方法关联效果更好。从图5可以看出，随着雷达测距误差的增大，两种方法的错误关联概率呈逐渐增大趋势，当雷达测距误差较大时，本文的关联方法具有更低的错误关联概率。

实验3：不同ESM测角误差对算法的影响，在其他条件同实验1完全相同的条件下，假设ESM测角误差为0.1°～1.2°，雷达测角误差为0.5°，分别进行100次蒙特卡洛仿真，图6和图7分别给出了不同ESM测角误差时雷达与ESM航迹正确和错误关联概率。

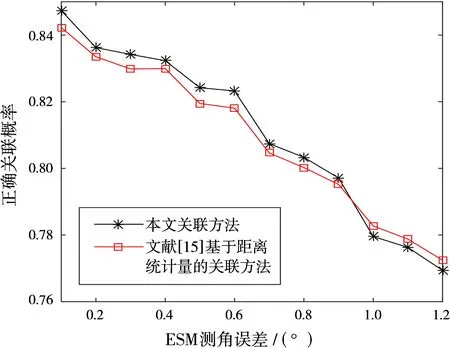
图6 不同ESM测角误差时雷达与ESM航迹正确关联概率

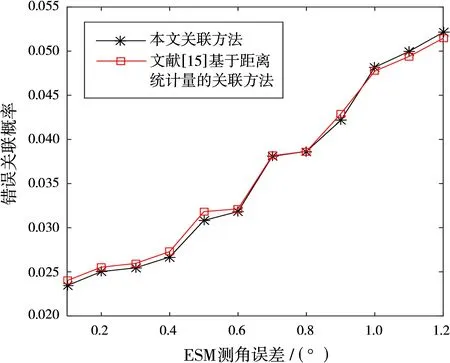
图7 不同ESM测角误差时雷达与ESM航迹错误关联概率

从图6可以看出，随着ESM测角误差的增大，两种方法的正确关联概率呈逐渐减小趋势，当ESM测角误差小于1°时，本文的关联方法的正确关联概率大于现有方法。从图7可以看出，随着ESM测角误差的增大，两种方法的错误关联概率性能相当，均呈逐渐增大趋势。

实验4：不同目标密集度对算法的影响，假设公共观测区域的目标数目为1～30，雷达测角误差为0.5°，在其他条件同实验1完全相同的条件下分别进行100次蒙特卡洛仿真，图8和图9分别给出了不同目标数目时雷达与ESM航迹正确和错误关联概率。

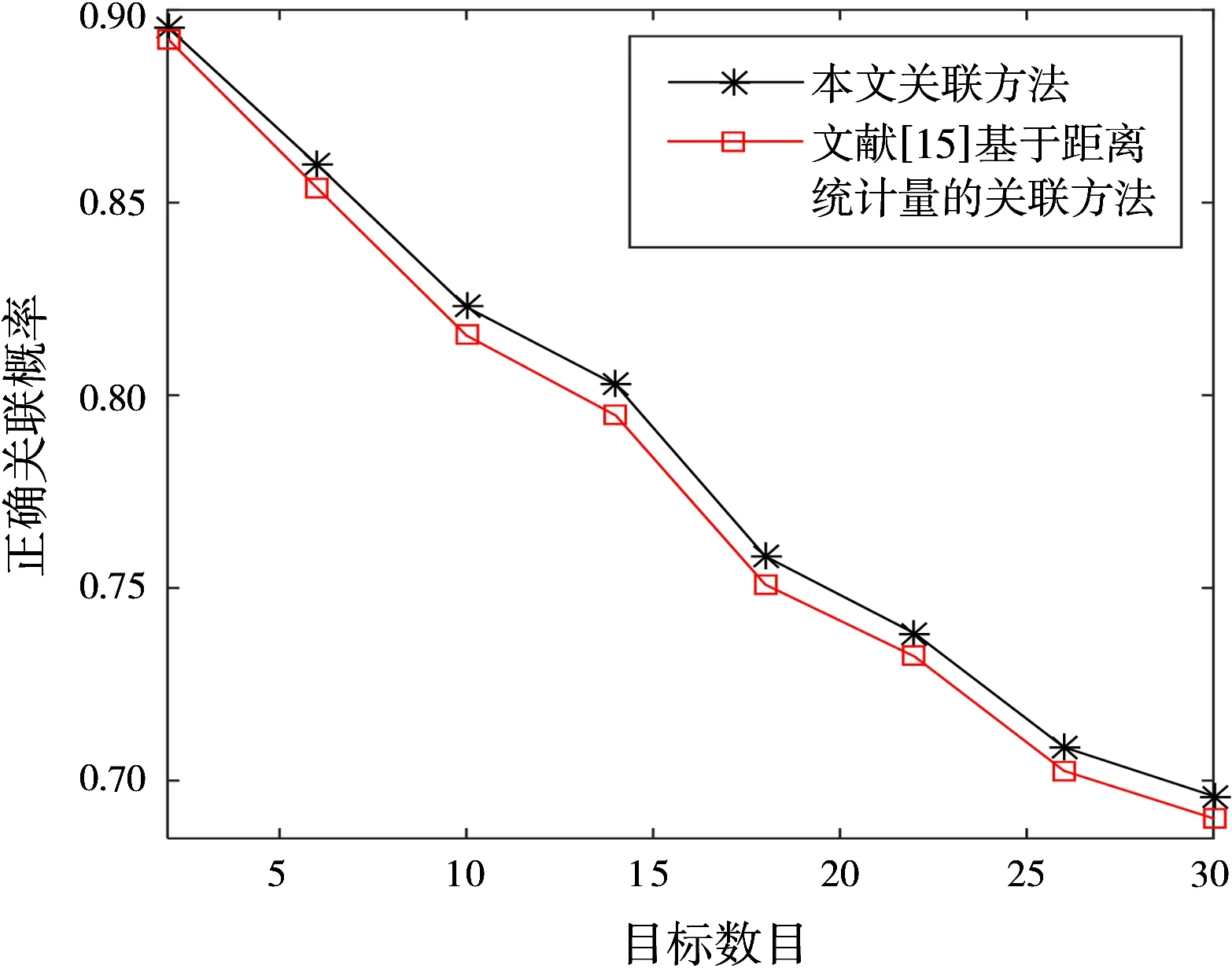
图8 不同目标数目时雷达与ESM航迹正确关联概率

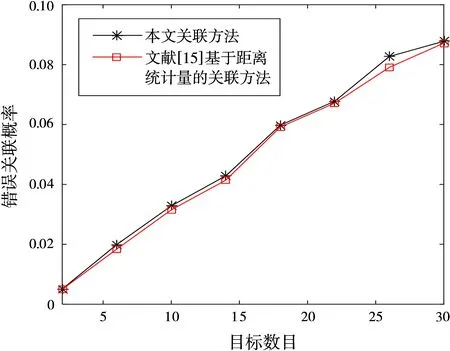
图9 不同目标数目时雷达与ESM航迹错误关联概率

从图8可以看出，随着目标数目的增大，两种基于统计理论方法的正确关联概率呈逐渐减小趋势，本文的关联方法的正确关联概率始终大于现有方法。从图9可以看出，随着目标数目的增大而增大，两种方法具有类似的错误关联概率。

4 结束语

本文研究了异地配置下的雷达与ESM航迹关联问题，提出了利用ESM虚定位点与交叉定位点来构造距离统计量的关联算法，并与文献[15]中基于距离统计量的关联算法进行了仿真对比。仿真结果表明，当目标数目相同时，本文提出的关联方法在雷达测角误差较小、雷达测距误差较大或ESM测角误差较小时具有更好的关联性能；当量测误差相同，本文方法在不同的目标密集程度时均有较好的关联性能。

[1] 韩崇昭,朱洪艳,段战胜,等. 多源信息融合[M]. 2版. 北京：清华大学出版社, 2010.

[2] 何友,王国宏,关欣,等. 信息融合理论及应用[M]. 北京：电子工业出版社, 2010.

[3] 杨万海. 多传感器数据融合及其应用[M]. 西安：西安电子科技大学出版社, 2004.

[4] 王国宏. 利用角度、角度变化率和ITG信息的主被动传感器数据关联[J]. 雷达科学与技术, 2003, 1(1):39-45.

[5] WANG G H, MAO S Y, HE Y. Analytical Performance Evaluation of Association of Active and Passive Tracks for Airborne Sensors[J]. Signal Processing, 2003, 83(5):973-981.

[6] WANG G H, MAO S Y, HE Y, et al. Triple-Threshold Radar-to-ESM Correlation Algorithm When Each Radar Track is Specified by Different Number of Measurements[J]. IEE Proceedings:Radar, Sonar and Navigation, 2000, 147(4):177-181.

[7] 刘德浩,王国宏,陈中华. 基于EM-EKF的异类传感器系统误差配准算法[J]. 雷达科学与技术, 2011, 9(5):453-456.

LIU Dehao, WANG Guohong, CHEN Zhonghua. A Registration Algorithm of Different Sensors Based on EM-EKF[J]. Radar Science and Technology, 2011, 9(5):453-456.(in Chinese)

[8] 黄友澎,曹万华,张志云,等. 基于灰色关联分析的异类传感器航迹相关算法[J]. 华中科技大学学报(自然科学版), 2011, 39(10):83-86.

[9] WANG G H, ZHANG X Y, TAN S C. Effect of Biased Estimation on Radar-to-ESM Track Association[J]. Journal of Systems Engineering and Electronic, 2012, 23(2):188-194.

[10] ZHOU Y F, MICKEAL J. A Sequential ESM Track Association Algorithm Based on the Use of Information Theoretic Criteria[C]∥10th International Conference on Information Fusion, Quebec:IEEE, 2007:1-7.

[11] 龙海鹰,任清安. 空管异类传感器数据融合算法研究[J]. 雷达科学与技术, 2010, 8(6):526-531.

[12] GUAN X, HE Y, YI X. Gray Track-to-Track Correlation Algorithm for Distributed Multitarget Tracking System[J]. Signal Processing, 2006, 86(11):3448-3455.

[13] 李彬彬,冯新喜,王朝英,等. 异类传感器三维空间数据关联算法研究[J]. 宇航学报, 2011, 32(7):1632-1638.

[14] 王妍妍. 基于GAM模型雷达与ESM数据关联实现方法[J]. 指挥信息系统与技术, 2012, 3(3):40-43.

[15] 王国宏,邵锡军,潘哲. 主被动传感器异地配置下的数据关联[J]. 现代雷达, 2003, 25(4):26-29.

[16] 宋振宇,张翔宇,张光轶. 系统误差对异地配置的雷达和ESM航迹关联的影响[J]. 电光与控制, 2014, 21(3):42-46.