LFMCW车载防撞雷达信号处理模块研究
2016-03-13,,,
, ,,
(东南大学信息科学与工程学院, 江苏南京 211189)
0 引言
随着经济的发展,公路交通运输量日益增大, 汽车作为主要运输手段,已成为当今社会生活中不可缺少的工具。随着汽车数量的快速增加,交通事故频繁发生,由此导致的生命财产损失数目惊人。车载雷达对于减少司机的负担和错误判断、提高交通安全以及降低恶性交通事故发生率将起到重要的作用。
调频连续波(FMCW)雷达具有结构简单、无测距盲区等优点,特别适用于汽车防撞雷达[1]。目前,调频连续波雷达一般采用三角波或锯齿波作为发射波形。三角波体制雷达计算复杂度低,但存在多目标配对困难的问题,可通过改变三角波扫频周期去除虚假目标[2]。锯齿波体制雷达通过二维FFT对速度和距离解耦合,计算复杂度较高[3]。车载防撞雷达应用场景比较复杂,雷达接收信号中除了目标回波,还有雷达接收机噪声信号、路旁护栏杂波信号和大型建筑物回波信号等,这些杂波干扰信号都会影响雷达对目标的检测,如何抑制这些杂波信号是保证车载防撞雷达检测性能的一个关键问题。数字波束形成技术可以形成窄波束以抑制感兴趣范围外的杂波干扰目标回波信号,提高检测概率[4]。实际应用中,由于雷达体积和成本限制,一般接收天线阵列较小,影响波束形成杂波抑制性能。
本文设计了一种低复杂度的信号处理模块。在预处理阶段,对频域信号进行相位校准,合成一个具有更大孔径的等效虚拟阵列接收信号,并利用加窗波束形成抑制杂波干扰信号,提高检测概率。在恒虚警检测中,本文提出一种改进CFAR算法,通过自适应改变噪声电平估计样本,减小目标峰值对后续频谱单元干扰噪声电平估计的影响。针对三角波的多目标配对,本文提出一种多步匹配算法,利用先验信息压缩匹配空间,降低配对复杂度,并有效去除虚假目标。
1 系统特点及波形选择
该车载防撞雷达系统主要用于侦测前向及相邻两车道内的车辆,并获取前向物体的距离、速度和方位角信息,信息更新频率为20 Hz,作用有效距离为2~70 m,应用环境中存在的路旁金属护栏、指示牌和高楼等杂波干扰信号严重影响雷达的性能。
综合考虑雷达尺寸、成本和方位角估计精度等因素,系统采用2×3的天线阵列。由于系统硬件限制,两个发射天线不能同时或者通过频率分集发射信号,因此本系统通过时间分集方式,两根天线轮流发射相同的宽波束调频连续波,通过相位校准可将接收的不同发射天线的目标回波信号合成一个具有更大孔径的虚拟接收阵列信号,并对虚拟阵列接收信号采用数字波束形成窄波束抑制杂波干扰信号,根据目标中频信号进行多目标检测和距离、速度及方位角估计。
目前,连续波雷达一般采用三角波或锯齿波作为发射信号波形,为降低成本,本系统选用存储空间需求小、计算复杂度较低的三角波作为发射信号波形。
2 三角波雷达测距、测速原理
雷达通过天线向前方发射调频连续波,并接收目标的反射信号。考虑目标前方存在一个距离为r、相对速度为v(以靠近雷达为正)的目标,变周期三角波发射信号与目标反射信号时频关系如图1所示。

图1 变周期三角波体制雷达信号时频关系图
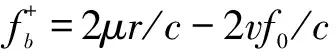
当存在多个目标时,采用单一扫频周期的三角波信号存在多目标配对问题,一些文献提出了MTD频域配对法[5],根据相同目标回波的中频信号具有相似的频谱峰值、频谱宽度等进行配对。这些方法会存在相似目标配对紊乱、计算复杂等缺点。在实际雷达系统中一般采用变周期三角波进行多目标的配对[6]。
假定存在n个目标,则在第i(i=1,2)个扫频周期的上扫频段目标j(j∈{1,…,n})的中频信号频率与下扫频段目标k(k∈{1,…,n})的中频信号频率配对的结果为
(1)
(2)
式中,μi=B/Ti,Ti为第i个扫频周期。
由式(1)和式(2)可以看出,真实目标距离和速度与μi是无关的,即在两个扫频周期内进行配对得到的距离和速度结果是相同的,而虚假目标的速度和距离结果不同。如果两个不同扫频周期内的两组距离和速度值相同,则认为该组值为某一个目标的距离速度参数值。
3 算法模块设计
3.1 信号预处理
3.1.1 相位校准
在连续波雷达系统中,最简单的数字波束形成系统可以由一个发射天线和多个接收天线组成,发射天线发射一个宽波束覆盖指定的区域,对中频采样数据进行快速傅里叶变换(FFT),然后对频域信号进行波束形成,抑制杂波干扰信号。
本系统采用2×3的天线阵列,采用时间分集的方式通过两个发射天线轮流发射相同的信号,3个接收天线接收目标回波信号。由于系统要求的角度测量精度需达到1°,为获得更高的测角精度,通过将接收的不同发射天线的目标回波信号合成,使2×3的天线阵列变为1×6的虚拟天线阵列,获得更高的测角精度和波束形成增益[7],如图2所示。

图2 虚拟阵列
如图2所示,两个发射天线间距为3d,接收天线间距为d,d=λ/2,λ为波长。虚拟阵列接收信号由接收天线阵列分别接收发射天线1和2的发射信号所对应的目标回波信号组成。由于系统采用时间分集发射信号,发射间隔内目标运动引起的相位差异使得虚拟阵列天线3和4之间的相位差Δφ3,4=φ4-φ3≠φd(φd为天线间距引起的相位差),在高信噪比条件下,可以利用虚拟接收天线3,4和5进行校准。接收天线3和4之间的相位差Δφ3,4=φd+φv,φv为发射间隔内目标运动对应的相位变化, Δφ4,5=φd,则需补偿的相位差Δφ=Δφ4,5-Δφ3,4。
3.1.2 数字波束形成
雷达接收信号中的杂波干扰信号会影响雷达对目标的检测,通过对阵列接收信号采用加窗数字波束形成技术形成窄波束接收,获得阵列增益的同时抑制感兴趣范围以外的杂波干扰信号,提高目标检测概率。对进行相位校准后的频域信号进行波束形成,如图3所示。

图3 数字波束形成
图3中,h=[h1,…,h6]T=(w⊙as(θ))H为复权矢量,窗函数w提供旁瓣控制的数据加权;导向矢量as(θ)提供对来自θ方向的信号的最大相干积累,z为波束形成输出矢量。
考虑一个单目标信号,对目标所在频谱通道的复矢量进行相位校准和波束形成,仿真结果如图4所示。

图4 波束形成增益对比
如图4所示,由于FFT(FFT点数:256)后能够得到较高的信噪比,与均匀线性阵列相比,虚拟阵列相位校准对波束形成增益影响很小。
3.2 恒虚警检测
3.2.1 CFAR检测算法
准确设定检测门限的前提条件是精确已知干扰功率,但是对一般雷达系统而言,干扰功率是未知的。为使雷达系统具有恒定的虚警概率,实际干扰噪声功率电平可以实时地从数据中进行估计,从而相应地调整雷达检测门限[8]。恒虚警检测的原理如图5所示。
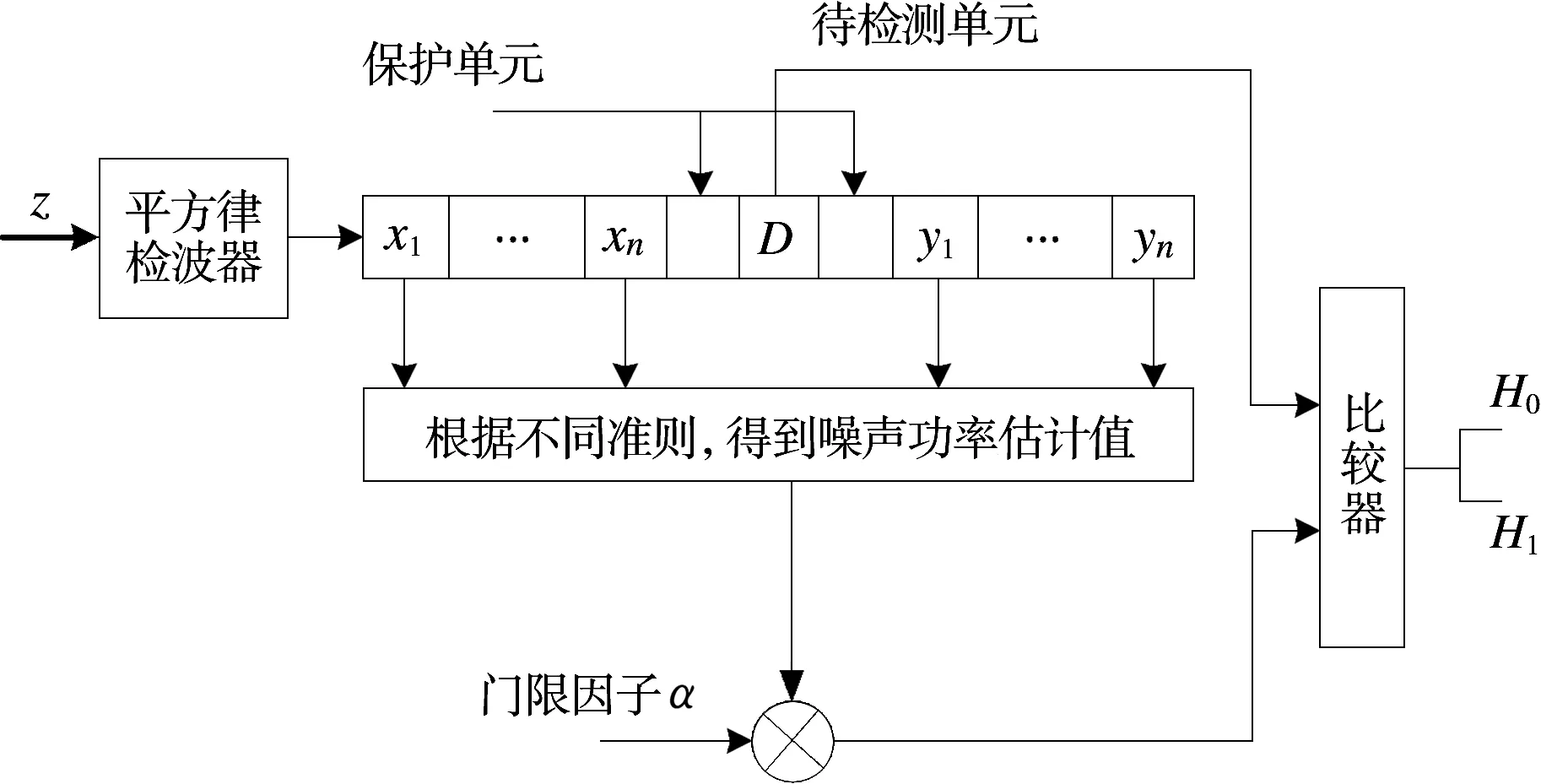
图5 CFAR检测
针对多目标应用场景,如果干扰目标存在于两个参考窗内,采用单元平均(CA)CFAR将会使噪声功率估计值变大,增大漏警率。单元平均选小(SOCA)CFAR算法对两个参考窗分别求均值,选取两个估计值中更小的值,该值更可能接近噪声功率,但在杂波边缘处会产生虚警。单元平均选大(GOCA)CFAR算法与SOCA CFAR算法相反,选取两个估计值中较大的,能够避免杂波边缘处的虚警,但对多目标的遮蔽效应较敏感。有序统计(OS)CFAR算法对参考单元内的数据进行升序排序,选择其中第kOS个元素作为干扰功率电平的估计,对于由紧邻目标引起的遮蔽效应极不敏感,但是复杂度较高[9]。
3.2.2 CFAR检测算法改进
车载雷达应用场景比较复杂,多目标遮蔽效应会导致漏检率增大,本文提出一种自适应改变噪声电平估计样本的改进CFAR算法。在CFAR检测过程中加入一个反馈操作,当该频谱单元存在目标时,用估计得到的干扰噪声功率电平代替该频谱单元值,减小对后续频谱单元干扰噪声功率电平估计的影响,从而减小目标遮蔽效应。改进CFAR算法的步骤为:
待检测矢量z=[z1,z2,…,zM];
fori=1∶M

该频谱单元存在目标;

end
end
综合考虑性能与复杂度,本系统采用单元平均选小准则的改进CFAR算法,与SOCA CFAR算法的检测性能对比如图6所示。
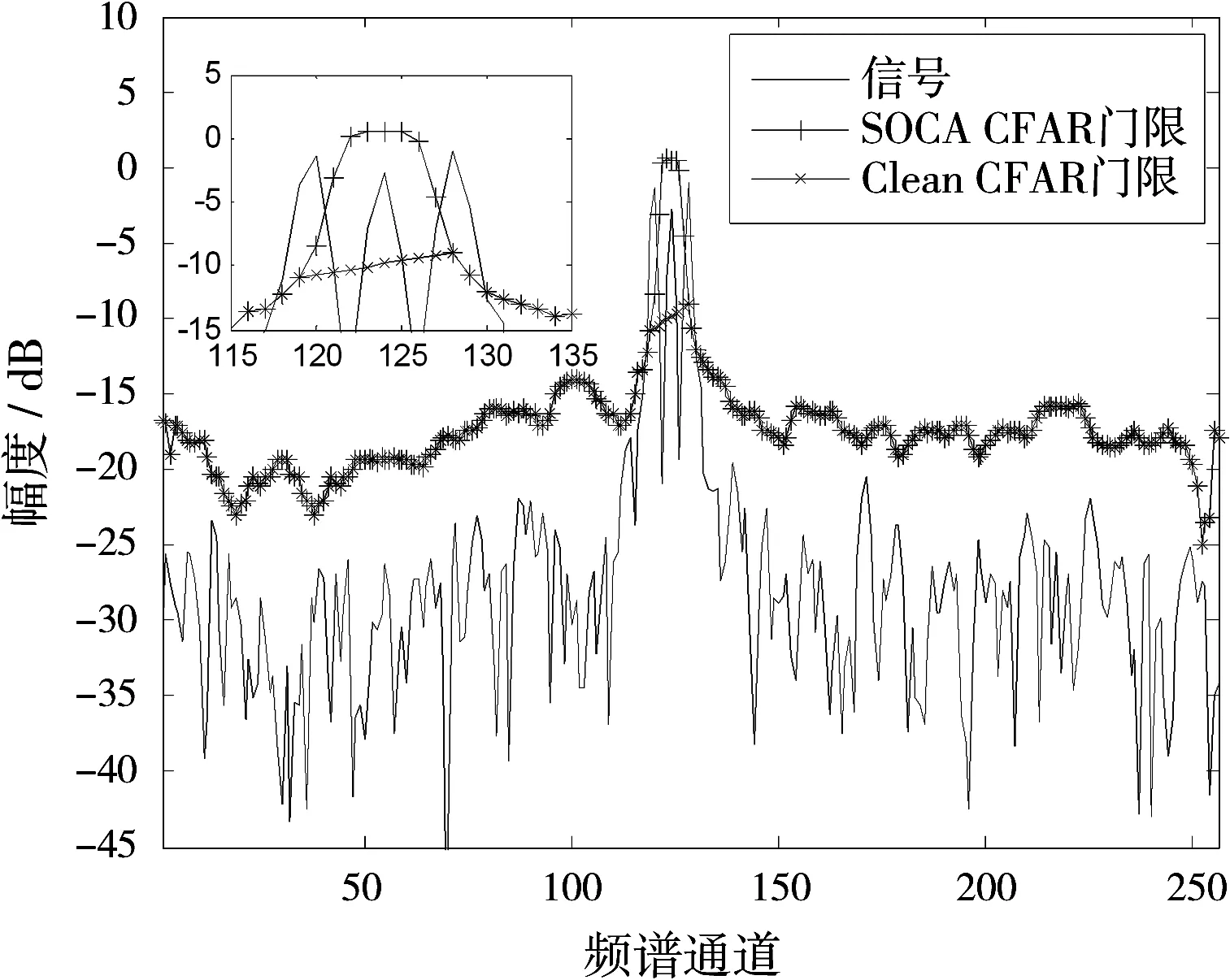
图6 CFAR算法对比
如图6所示,存在3个频谱位置相近的目标,采用改进的CFAR算法能够正确检测到全部目标。在检测到目标后,用估计的噪声功率电平替代目标峰值,避免目标频谱峰值对邻近频谱单元干扰噪声功率电平估计的影响,有效减小目标遮蔽效应。
3.3 变周期多目标配对
3.3.1 容差函数配对算法
由于实际中频信号频率计算不可避免地存在误差,在判断两个速度距离信息组合是否相等时需要建立容差函数,如果两者的误差在容差内,则判断是相等的[10]。
假设中频信号采样频率为fs, FFT点数为NFFT,则得到的信号频谱观察细度为Δf=fs/NFFT,由此可根据式(1)计算FMCW雷达的测距精度为Δr=cTfs/2BNFFT,建立目标的距离容差函数:
(3)
如果在两个周期内测得的距离差小于此容差值,则认为相等。
同理,可以建立速度容差函数:
(4)
但在实际工程中,由于采用的FFT点数较少等原因,会导致距离和速度容差函数值较大,只利用容差函数值,结果中仍存在较多虚假目标。针对这个问题,本文提出一种利用先验信息压缩匹配空间的多步配对算法,能够在频率配对过程中有效去除虚假目标,并降低计算复杂度。
3.3.2 多目标配对算法改进
在三角波体制雷达中,虽然仅根据一个扫频段的中频信号频率值无法得到目标的距离和速度信息,但可以利用先验信息,根据同一目标在不同扫频段的中频信号频率间的内在联系压缩频率配对空间,去除虚假目标。
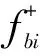
(5)
式中,vmax为系统感兴趣范围内的最大相对速度。

(6)
(7)
变周期多目标配对算法具体步骤为:
1) 相同扫频周期上下扫频段配对:
fori=1∶N1
计算能够配对的范围:
forj=1∶N2

度矩阵中对应的距离和速度值;
end
end
end
同理,进行第二个扫频周期的配对。
2) 不同扫频周期相同扫频段配对:
fori=1∶N1
计算能够配对的范围:

forj=1∶N3
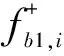
end
end
同理,进行下扫频的配对。
3) 容差函数配对:计算步骤1)和2)中均配对成功的组合对应的距离和速度差值,若均小于对应的距离和速度容差函数值,则认为是同一目标。
4) 若某一检测结果在另一扫频周期中存在多个配对结果,则计算速度-距离平面的欧氏距离,取最短距离对应的配对结果。

3.4 方位角估计及点迹凝聚
3.4.1 波达方向估计算法的选择
针对配对得到的目标,利用目标所在阵列频谱通道的复矢量对其方位角进行估计。目前,工程上常用的方位角估计算法有比相法、和差波束法、Music法、Esprit法和Capon法等。由于车载防撞雷达系统应用场景比较复杂,一个频谱通道内可能存在多个目标的回波信号,采用比相法或和差波束法会有较大误差,Music法需要对源目标个数进行估计,Esprit法稳健性较差。综合考虑,选择稳健性较高的Capon法进行方位角估计。
3.4.2 波达方向估计的稳健性修正
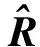
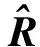
(8)

3.4.3 点迹凝聚
系统信息更新频率为20 Hz,即一帧时长为50 ms。一帧时间内会进行多次检测,同一目标可能会检测出多个相距较近的点,采用质心法对点迹进行凝聚,点迹凝聚算法步骤为:
1) 找出(剩余)点迹中幅度最大的点;
2) 搜索以该点为中心,角度差小于2°、距离差小于1 m的点迹,采用质心法对距离、速度及角度信息进行凝聚;
3) 重复步骤1)和2),直到遍历所有点。
一帧内进行K次检测,目标被正确检测次数大于(等于)K0次,则进行点迹凝聚,否则作为虚假目标舍去,K0大小根据漏警率和虚警率决定。
4 算法仿真结果
雷达系统部分参数如表1所示。

表1 雷达系统参数表
设置3个车道,本车雷达处于中间车道(图7中原点位置),在雷达前方设置多个目标以及指示牌,道路两旁存在护栏,目标车辆RCS=20 dBm2,接收信号信噪比根据雷达方程计算得到,目标相对位置如图7所示。
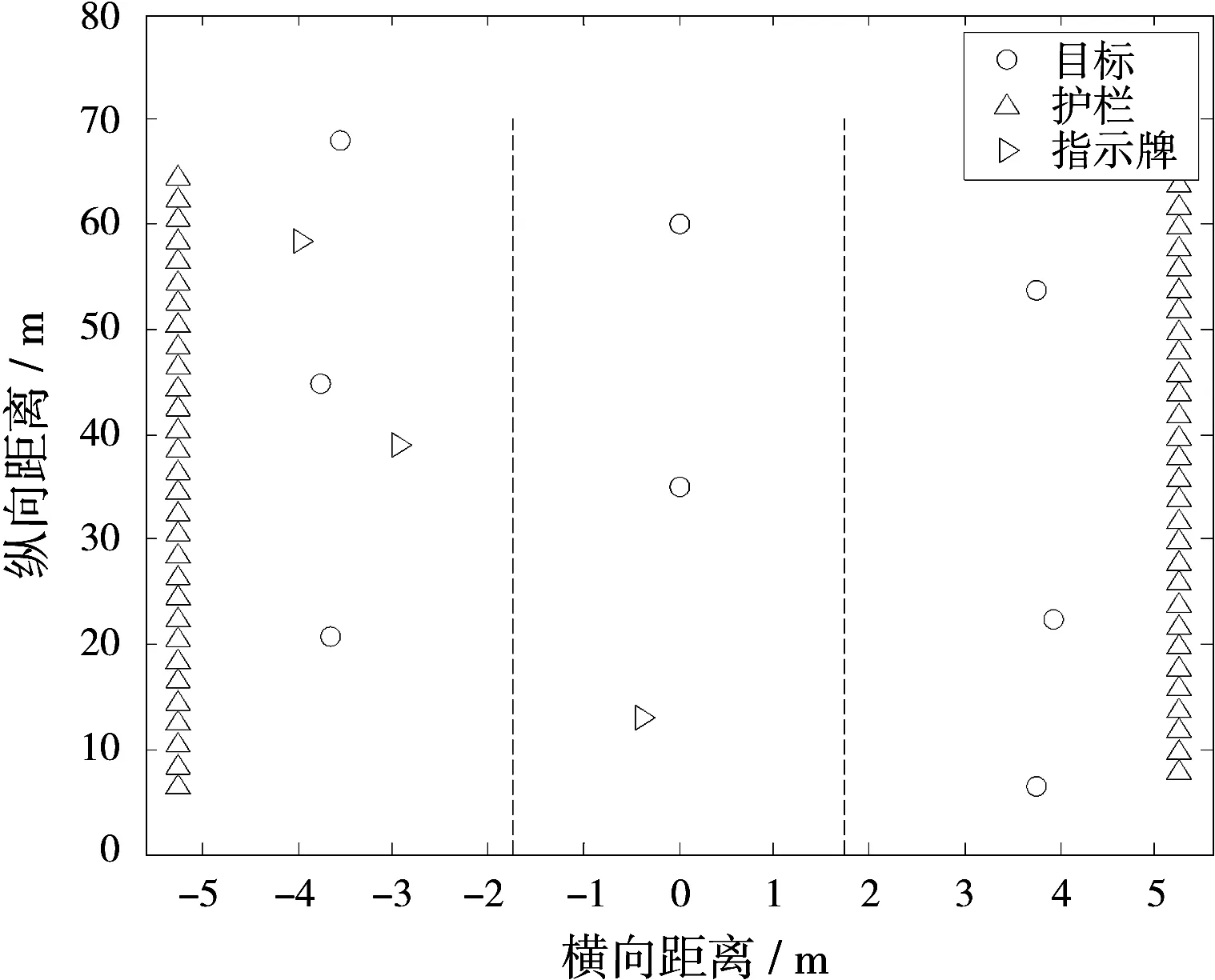
图7 仿真场景示意图
采用本文设计算法进行多周期目标检测,检测结果如图8所示。

图8 仿真结果
如图8所示,所有目标均被正确检测,没有产生虚假目标,部分路旁护栏杂波也被检测。将仿真结果与实际值比较,目标测距误差均值为0.48 m,测速误差均值为0.16 m/s,测角误差均值为0.12°,均在系统误差允许范围内。
5 结束语
本文设计了一种LFMCW车载防撞雷达系统信号处理模块,该模块通过合成虚拟阵列获得更大的接收天线孔径,采用数字波束形成窄波束对感兴趣范围内目标进行检测,采用自适应改变噪声电平估计样本的改进恒虚警检测算法有效减小了目标遮蔽效应,同时利用基于先验信息的多目标配对算法压缩配对空间,在频率配对阶段能够有效去除虚假目标并降低计算复杂度。仿真结果显示,该算法能正确检测出雷达前方目标,误差均在系统允许范围内。
[1] 简森林,何宗锐. 基于步进频连续波雷达的射频对消[J]. 雷达科学与技术, 2016, 14(2):189-193.
[2] LIN J J, LI Y P, HSU W C, et al. Design of an FMCW Radar Baseband Signal Processing System for Automotive Application[J]. Springerplus, 2016, 5(1):1-16.
[3] SONG M, LIM J, SHIN D J. The Velocity and Range Detection Using the 2D-FFT Scheme for Automotive Radars[C]∥IEEE International Conference on Network Infrastructure and Digital Content, Beijing:IEEE, 2014:507-510.
[4] WANG W,WANG R, DENG Y, et al. Improved Digital Beam-Forming Approach with Scaling Function for Range Multi-Channel Synthetic Aperture Radar System[J]. IET Radar, Sonar and Navigation, 2016, 10(2):379-385.
[5] 杨建宇,凌太兵,贺峻. LFMCW雷达运动目标检测与距离速度去耦合[J].电子与信息学报, 2004, 26(2):169-173.
[6] ISSAKOV V. Microwave Circuits for 24 GHz Automotive Radar in Silicon-Based Technologies[M]. Berlin:Springer, 2010:9-11.
[7] FISCHER C, ANDRES M, BLOECHER H, et al. Adaptive Super-Resolution with a Synthetic Aperture Antenna[C]∥9th European Radar Conference, Amsterdam:IEEE, 2012:250-253.
[8] RICHARDS M A. Fundamentals of Radar Signal Processing[M]. New York:McGraw-Hill, 2005:260-263.
[9] TAO D, ANFINSEN S N, BREKKE C. Robust CFAR Detector Based on Truncated Statistics in Mul-tiple-Target Situations[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 54(1):1-18.
[10] 宋洋. 一种改进的车载雷达多目标检测方法[J]. 电子科技, 2014, 27(11):135-138.
