数学教学中如何拓展学生的思维能力

☉江苏省苏州市吴县中学 韦莉

数学教学中如何拓展学生的思维能力

☉江苏省苏州市吴县中学 韦莉

对高中数学进行过一段时间的学习之后便会深切地感受到，与初中数学学习相比，高中数学的内容明显复杂了许多.无论是从知识方法的数量来讲，还是从具体问题的思维难度来讲，均呈现出了显著提升的趋势.也正是如此，越来越多的学生对数学学习感到困惑，甚至信心不足，失去兴趣.面对这一现状，教师作为教学活动的主导者与维护者，有必要从旁引导和帮助学生，为学生们提供一些全新的问题思考途径，不断拓展思维，推动高中数学学习走向高效.

一、巧用平移，整合零散已知条件

平移是立体几何中十分常用的一种问题分析方式，就是将图形中的某个部分进行平行移动，以便进行新图形的构造或是对当前部分进行比较，完成问题解答.平移的思维，关键在于对运动状态的把握.从前面的介绍中不难发现，对图形进行平移，实际上就是一个等价转换的运动过程.只要能够让学生们明确了“该动哪里”和“该动到哪里”这两个问题，平移的思维就成功建立起来了.

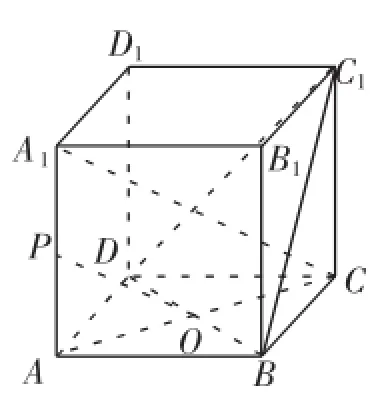
图1

例如，在学习过直线与平面所成角的内容后，我为学生们设计了这样一道习题：如图1所示，在正方体ABCD-A1B1C1D1中，点P是棱AA1的中点，点O是底面ABCD的中心，那么，OP与平面BDC1所成的角是多少？在这个问题中，如果想要直接确定OP与平面BDC1所成的角，

并不十分容易.然而，A1C与这个截面之间的关系却是比较好找的，又不难发现，A1C与OP是平行的，自然可以通过平移进行代换，求出A1C与平面BDC1所成的角，同时也就是题目所求了.这个平移的过程并不复杂，却让待求问题的分析思路一下子明朗了许多.

平移方法的运用并不困难，且只要将之运用得恰如其分，往往能够使得复杂的问题迎刃而解.巧用平移，最重要的一点在于学生们是否具备了运动的眼光.如果几何图形在学生们的眼中始终是固化的，那么，再明显的平移条件也难以被学生所发现.只有大家让眼前的图形动起来，明确自己想要的图形状态，找到合理的移动方式，才能将平移思维运用自如.

二、巧用等积，寻找数学推导中介

当学生们面对一些条件繁杂的数学问题时，常常不知道如何将之进行串连与处理，使得思维愈发混乱，无法顺利解题.这时，如果能够将这些看似毫无关联的已知条件向着同一个分析目标进行“翻译”，便能够拨云见日，发现题目条件中的共同指向，由此找到解答问题的正确途径.那么，如何才能有效完成“翻译”的工作呢？我们往往需要找到一个适当的中介，协助我们完成推导过程中的等价转化.

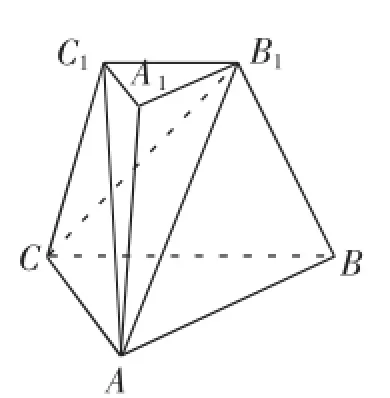
图2

例如，在对棱锥与棱台的内容进行学习时，学生们遇到了这样一个问题：如图2所示，三棱台ABCA1B1C1的上、下底面面积分别是a2，b2，底边BC与截面AB1C1之间的距离等于此三棱台的高.那么，该截面AB1C1的面积是多少？在这个问题中，既有长度，又有面积，还有体积，学生们一下子不知道应当如何找思路.我启发学生：既然这些元素都在同一个棱台中，且共用一个高，何不从体积的角度来进行分析呢？于是，学生们连结B1C，并将三棱台分解为A-A1B1C1、B1-ABC和C-AB1C1三个三棱锥，通过三者体积之和等于棱台体积的关系，顺利求得答案.

等积思想在高中数学的几何问题中运用得十分广泛.当然，笔者只想把等积思想作为一个代表，以之向广大师生们传递一种寻找适当中介，进行转换转化的思维意识.在高中数学问题中，不可能每个条件都表述得很直接.想要将已知条件充分运用，就要学会借力转化.

三、巧用分割，问题有效化繁为简

很多学生在解答数学问题时总会感到思维上十分混沌，面对数量庞大的条件内容交织在一起，不知道应当如何将之区分开来.这样一来，原本复杂的问题，在学生们的眼中不免变得更加复杂了.如果这种情况经常性地出现，必将对学生们的解题心理造成极大障碍，于高中数学有效教学来讲更是非常不利的.其实，数学中的复杂问题并不可怕，如果感到其中的条件元素过于集中，只要将它们分割开来就可以了.

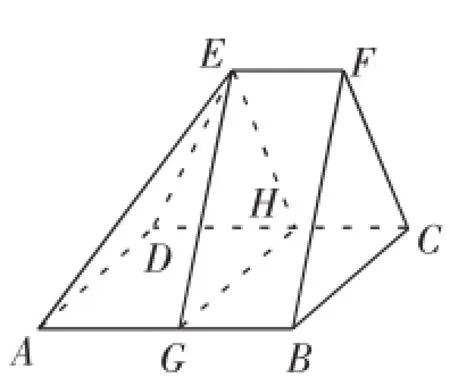
图3

例如，学生们在一次测验中曾经遇到过这样一个多面体的问题，解答起来感到比较困难：如图3所示，在多面体ABCDEF中，ABCD是边长为3的正方形，且AB与EF平行，EF长为1.5，EF与平面ABCC之间的距离为2，那么，此多面体的体积是多少？对于不规则的多面体，学生们从来没有学过如何计算其体积.于是，便需要从既有知识出发，对该多面体进行改造.不难发现，若构造出一个截面EHG，使之将多面体截为一个三棱柱与一个四棱锥，问题瞬间迎刃而解了.这就是分割思维的巧妙运用.

在高中数学中，分割是一种具体方法，更是一种思维方式.恰如前文所列举的，在立体几何中，若是出现了较为复杂的几何体，或是伴随着十分杂乱的相关条件时，往往可以采取分割的方法，将其剥离成为几个相对独立的简单目标，各个击破，难度顿时降低不少.

四、巧用补形，实现新旧知识迁移

如果说上述的分割是一种“拆”的思维方式的话，那么，与之相对应，就存在着“补”的思想.学生们所面临的数学问题，除了条件太多，难以剥离的状况，还有条件太少，无从下手的情形.这种情况的出现，往往更容易让学生们感到束手无策.为此，笔者在向学生们传授过分割的思想之后，又马上提出了补形的理念.

例如，在学习过二面角的知识内容后，我请学生们试着解答如下习题：如图4所示，AA1与正方形ABCD所在平面垂直，且BC=AA1，那么，平面A1CD与平面AA1B所成的二面角（锐角）是多少？在这样的图形状态下求两个平面所成的二面角，虽然不是不可以，但思维过程却十分复杂，且容易出错.于是，我抓住这个几何体的特点，带领学生们将之补形成为了一个正方体（如图5）.正方体是学生们再熟悉不过的几何体了，在正方体中求二面角，难度也降低了许多.

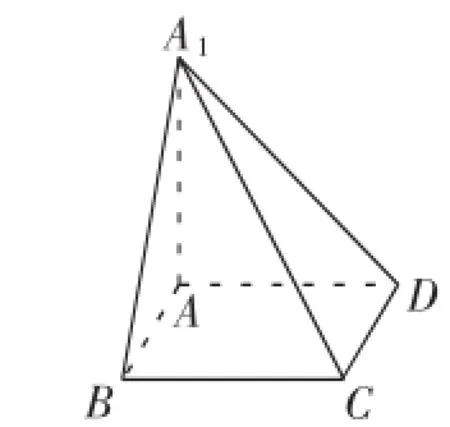
图4

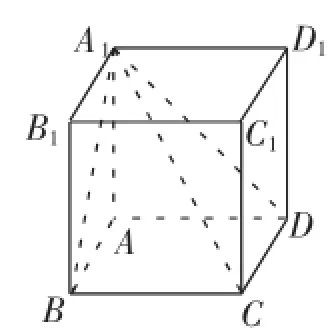
图5

一拆一补，数学问题的解答思维瞬间拓展完善了许多.对于条件充裕的问题，适当拆分，化整为零；对于条件不足的问题，巧妙补充，搭建平台.在这样的思维过程中，学生们的思路始终是灵动的.高中数学就是这样，对于学生们的思维灵活性要求非常之高.对于任何一个问题，学生们都需要以运动变化的眼光来看待和分析，才能够找到解题捷径，在快捷高效的动作中完成题目解答.

五、巧用展开，立体平面快速过渡

本文最后所强调的展开思维，主要针对的是几何问题的解答.想要准确解答几何问题，学生们的空间想象能力必须过关.然而，再完备的空间想象能力，不一定能够保证每一个问题的高效解决.有些问题，并不是仅从立体的角度就能顺利分析的，而有些问题，如果能够以平面的眼光来加以看待，反而可以更加快捷地得出答案.

例如，在三棱锥内容的教学过程中，曾经出现过一道很有意思的题目：如图6，正三棱锥S-ABC的底面边长为a，侧棱长为2a，点E和点H分别为BS和CS上的动点，那么，EA+EH+AH的最小值是多少？怎样才能让三者之和最小？是将每条线段的长度都取得最小吗？同时满足最小值的条件，似乎是不现实的.在我的启发之下，学生们发现，三条线段正好围成了一圈.那么，如果三者构成一条直线，距离自然是最短的.于是，便产生了将三棱锥展开（如图7）的思路.在展开图上使得A，E，H，A′四点共线时，三者之和取得最小，具体数值计算起来也就容易多了.

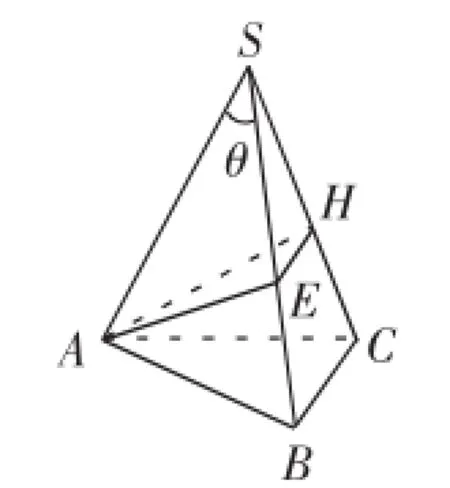
图6

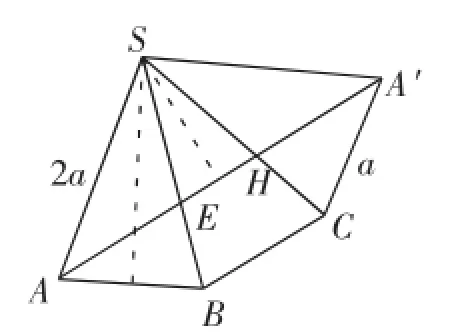
图7

可以看出，高中数学中的立体几何内容，并不是在三维空间中独立存在的.在很多情况下，立体几何问题的解答过程需要依赖平面几何的帮助.在立体与平面之间的过渡转化中，代数的方式也得以更为顺利地融入进来.在多个思维角度的整合之下，学生们必然能够将立体几何问题准确快速地予以解决.

从以上分析中不难发现，虽然都是同一个部分的知识内容，却也存在着不同种类的思维方法.随着具体问题的不同，需要进行分析的入手点也不同.学生们只有将每一种思维方式都熟练知晓，并结合实际问题进行特点分析，方能实现最终的准确匹配，对特定的问题采取相应的方法予以解答.在这样的思想指导下，整个高中数学领域中的问题解答都将实现思维创新与实效提升.Z