基于VSM-GA的建筑施工流程优化

仲珺怡，　苏振民，　佘小颉

(1. 南京工业大学　土木工程学院， 江苏　南京　211816； 2. 江苏顺通建设集团有限公司， 江苏　南通　226400)



基于VSM-GA的建筑施工流程优化

仲珺怡1，苏振民1，佘小颉2

(1. 南京工业大学土木工程学院， 江苏南京211816； 2. 江苏顺通建设集团有限公司， 江苏南通226400)

摘要：当前建筑施工过程中存在着生产效率低下、过程稳定性差、资源浪费严重等问题，导致建筑行业生产效益低下，阻碍建筑行业的可持续发展，因此对建筑施工流程优化有着重要意义。本文构建了价值流程图(VSM)与遗传算法(GA)的整合框架，利用遗传算法的数据化择优功能弥补了价值流程图技术在方案选择时存在主观随意性的缺陷，从而更科学有效地对建筑施工流程进行优化。在整合框架的基础上提出VSM-GA的目标优化模型，模型建立了流程优化目标函数和精益工具效用系数矩阵并设置了多参数离散型的遗传算法运算规则，经运算得到了施工流程优化的最优组合方案。最后通过案例研究进一步阐述了基于VSM-GA的施工流程优化的具体实施过程，并验证了模型的可行性与有效性。

关键词：流程优化；价值流；遗传算法；精益建造

在建筑产业现代化潮流的时代背景下，迫切要求改变当前施工流程效率低下、稳定性差和资源浪费严重的现状，为此，许多研究学者致力于寻求能够有效提高效率和减少浪费的方法，其中绘制价值流程图(Value Stream Mapping，VSM)作为一种重要的精益方法得到了众多学者的关注[1]。

VSM在制造业中的成功应用表明其能够显著缩短生产周期、提高生产效率和减少生产过程中的浪费。因此，许多学者尝试将VSM运用于建筑业，以期改善建筑施工的生产过程。Yu等[2]以基础工程为研究对象，绘制基础工程施工的价值流程图并利用先入先出原则(First Input First Output，FIFO)、调整生产节拍时间等方法对施工流程进行优化，使生产周期缩减41.2%。Rosenbaum等[3]以混凝土墙施工为研究对象绘制其价值流程图，将可持续理念融入其中，识别出墙体施工过程中的生产资源和环境资源两方面的浪费，同时运用精益工具对价值流程图进行改进。其他学者则认为，VSM具有一定的局限性如VSM的静态属性和价值流未来图的实现率不高等问题，为此，Gurumurthy 等[4]和Erikshammar等[5]提出了VSM与DES(Discrete Event System)的整合模型，将其运用于建造业门窗商品的制造过程，利用DES的动态仿真性能将价值流程图中的改进措施进行可修改化和可视化。还有的学者将可持续理论融入VSM，Faulkner[6]等在前人的基础上构建Sus-VSM(Sustainable Value Stream Mapping)，用以评估生产可持续性、环境可持续性和社会可持续性。

然而，这些对VSM的改进虽使得VSM更加适用于建筑业，但仍然存在着以下几点不足：一是没有解决VSM内在的主观随意性即管理者仅根据经验和主观判断来实施VSM改进，难以达到理想的效果，精益工具的选择也往往是通过管理者的定性分析，缺乏数据支撑；二是没有考虑经济制约、资源均衡等外部客观因素，仅考虑工期的缩短难以满足现实需求；三是没有明确表达优化后实施精益计划的步骤，仅仅提供价值流现状图到价值流未来图的笼统的改进方向，难以实施精益计划。

因此，本文提出将遗传算法(Genetic Algorithm，GA)与VSM进行整合，利用GA的数据化择优功能弥补VSM的缺陷，实现定性与定量相结合、主观与客观相统一。通过设定多参数离散型的GA运算规则，使得VSM中涉及到的参数均被纳为GA优选的考虑因素，为实现流程优化的最优组合方案提供数据支持。

1VSM-GA的整合框架及模型构建

1.1VSM-GA的整合框架与实施步骤

为了解决传统VSM所存在的方案选择随意性、考虑因素单一性、改进计划笼统性等问题，在VSM改进过程中引入GA算法，从而优化VSM技术。

在数据收集阶段，除了收集绘制价值流现状图所需的数据外，还需收集该流程中有关工序的其他施工方案和数据，用于GA以便择优选取。在识别问题阶段，除了识别价值流现状图所需解决的问题外，还需识别该问题所涉及到的约束条件，用于形成GA的目标函数和约束函数。在选择精益工具阶段，除了对精益工具进行初步评估外，还需对各拟定的精益工具进行专家打分评估其具体的效用系数，用于GA以便客观、合理地选择精益工具。在实施精益计划之前，对输出的GA优化结果进行二次优化，从而指导精益计划的实施。具体的VSM-GA整合框架如图1所示。

图1　VSM与GA的整合框架

(1)数据收集

为了使VSM更好地运用于建筑业，一方面要对传统VSM所使用的关键概念如生产周期、库存等进行改进使其更好地适应建筑业。另一方面，由于建筑施工的不稳定性和一次性的特点，针对研究工序搜集类似项目的实际数据，并利用数据统计分析软件对收集到的数据进行处理，得到各指标的取值范围。

(2)绘制价值流现状图与施工方案表

价值流现状图是识别问题的基础，其质量好坏关系到能否清晰展现存在的浪费、能否正确识别待解决的问题、能否提出符合实际的改进方案及措施。因此，价值流现状图的绘制必须注重客观性、着重性、准确性和精确性。

(3)识别问题并确定基本目标函数

价值流现状图绘制完成后，通过观察和仔细分析识别出存在的问题如施工生产时间过长、有效工作时间百分比较低、准时开工率较低等，根据识别出的问题设定相应合理的目标函数。

(4)选择精益工具并构建效用系数矩阵

在价值流程图改进过程中，从精益建造理论出发，以顾客需求最大化为中心，运用精益工具可以显著减少施工流程中的浪费[7]。因此，针对价值流现状图中分析出的各种问题，初步拟定精益工具并采用专家评分法量化精益工具的效用，形成精益工具的效用系数矩阵，从而用于GA运算来获取最优的精益工具使用方案。

(5)运行GA算法并二次优化模型结果

在运行GA算法时，通过设定多参数离散型的GA运算规则，充分考虑VSM中涉及到的参数并快速优化。在获取优化结果后，通过综合系数、函数求导等方法进行二次优化，从而指导精益计划的实施。

(6)绘制价值流未来图并实施精益计划

经过两阶段优化得到目标函数优化值、采用的精益工具、各精益工具的优先顺序以及使用过程中的注意要点。此外，客观条件的改变会对施工流程产生影响，因此施工流程的优化应持续进行。

1.2VSM-GA的目标优化模型构建

(1)基本模型描述

首先，根据特定施工任务的实际情况和现实需求设定不同的改进目标，共设定K个改进目标函数：

O={f1,f2,…,fk,…,fK}

(1)

式中：O表示改进目标函数集；fk表示第k个改进目标函数。

其次，将施工中的某一特定工作任务分为M道工序，Xkm为第m道工序不使用精益工具时为求解第k个改进目标函数的实测数据集，则所有实测数据集A为：

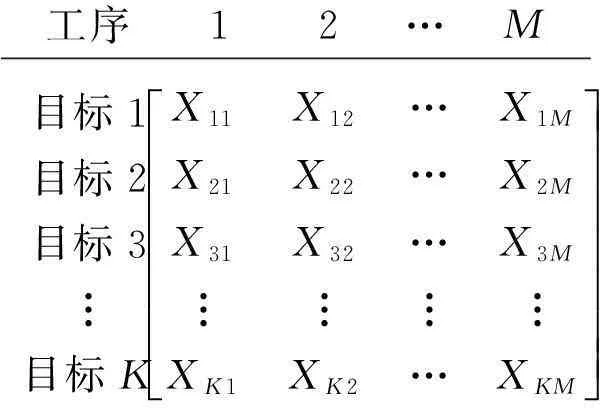
工序1 2 … M目标1目标2目标3︙目标KX11X12…X1MX21X22…X2MX31X32…X3M︙︙︙︙XK1XK2…XKMéëêêêêêêêùûúúúúúúú

(2)

再次，针对每一个改进目标下的每一道工序，统计计算n种不同的精益工具对各计算参数的作用效果系数，即Yim为第m道工序使用第i种精益工具时对各计算参数产生的作用效果，Ak为在第k个改进目标下由Yim组成的矩阵：

(3)

最后，在基本目标函数fk的基础上，考虑采用精益工具时对各目标函数的影响，从而拟定精益目标函数fk。

在价值流程图的改进过程中，通常会涉及工期、有效率、一次通过率、准时开工率等，这些目标函数的基本形式设置如下：

(4)

式中：CT表示整个施工任务所需的总工作时间；Di表示各道工序所持续的工作时间；Δi表示第i道工序的施工时间与第i+1道工序之间的库存时间。

maxf2(VTP)=(1-set/D-pt/D)×100%

(5)

式中：VIP表示每道工序中增值工作占该工序工作时间的百分比；set表示准备工作时长；pt表示施工过程中累计达到的工作中断时长。

maxf3(FPP)=θ×100%

(6)

式中：FPP表示一次通过率；θ为质量合格率。

maxf4(SSPm)=f4(SSP(m-1))×

(7)

式中：SSP表示每道工序的准时开工率；Rh表示第h种风险源所导致的工序无法按时开工的风险大小。

将矩阵(2)和(3)带入以上4个基本目标函数得到精益目标函数为：

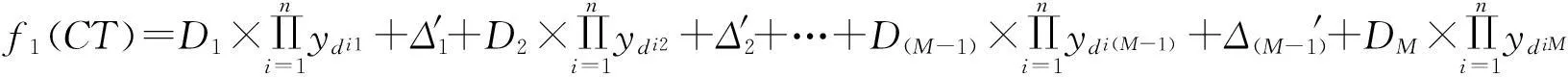
(8)

式中：ydim为第i个精益工具对第m道工序的“工期”产生的效用系数；Δm′为精益工具产生效用后第m道工序的库存时间。

(9)

式中：ysim和ypim分别为第i个精益工具对第m道工序的“准备时间”和“暂停时间”产生的效用系数。

(10)

式中：yθim为第i个精益工具对第m道工序的“一次合格率”产生的效用系数。

(11)

式中：f4(SSP(m-1))为第m-1道工序的准时开工率，当m=1时，f4(SSP(m-1))=f3(SSP(m-1))=1；yrim为第i个精益工具对第m道工序的延迟开工因素的风险产生的效用系数。

最终根据现场负责人和项目管理人员对各目标的需求程度，设置各目标权重ωk，形成GA综合目标函数，并根据需要设置GA约束函数：

式中：ωk为各目标函数的权重，φ为修正指数，ci表示各道工序及使用各精益工具所花费的成本，C表示可接受的成本上限。

(2)模型的求解

GA依据优胜劣汰的进化规则能够在众多可行域中查找问题解并快速优化[8]，因此它能够较好地处理上述模型中的大量数据，最终求得最优组合方案。

1)确定GA目标函数及染色体组成。

根据公式(12)设置目标函数，同时设置参数使程序将自动随机生成由S个染色体组成的初始种群，染色体Chrom长度为L。前M个基因座为工序基因Chrom1，其上的数字代表着不考虑精益工具时的方案序号；后L-M个基因座为精益基因Chrom2，其上的数字为0或1，0表示不使用该精益工具，1表示使用该精益工具。

2)设置适应度函数。将Chrom2转置为列向量，复制并扩展为n×M的矩阵B，根据公式(13)进行Ak与B的元素群幂次运算得Ak′。其中Ak为在第k个改进目标下由Yim组成的矩阵(见公式(3))。

Ak′=Ak·^B

(13)

将A与Ak′代入下列公式，得到各个染色体的适应度函数值Fit(fk(A,Ak′))。

(14)

3)选择、交叉和变异操作。采用轮盘赌法进行选择操作，即适应度越高的个体遗传到下一代的概率越大；采用单点法进行交叉操作，即在个体编码串中随机设置一个交叉点，在该点处相互交换两个配对个体的部分染色体；采用基本位法进行变异操作，即对个体编码串中以变异概率、随机指定的某一位或几位基因座上的值做变异运算。

4)输出最优组合方案及各子目标函数值f1(CT)、f2(VTP)、f3(FPP)、f4(SSP)。

(3)模型结果的二次优化

为了明确表达优化后实施精益计划的步骤及控制要点，采用综合系数和函数求导的方式对模型结果进行分析，根据二次优化结果指导精益计划的实施。

当Wi的值越大时，应当越优先使用第i个精益工具。

2)采用求导法使目标函数f对各参数进行求导，可量化对应的精益工具的影响力大小，为项目管理人员的科学管理提供依据。根据下列公式求得同一改进目标同一工序下各精益工具的影响力大小：

(16)

当Vi的值越大，说明相对于其他精益工具而言，该精益工具的潜力越大，越能影响目标函数值。在项目实施过程中，应当更加注重这些具有较大潜力的精益工具的实施。

2案例研究

2.1工程概况

新麓花园是一个较大的住宅建设项目，位于苏州新区，占地面积为130459.6 m2，共分为四期开发。其中三期四标段共计14幢楼，11幢为6层低层住宅，3幢为17层高层住宅，建筑结构形式为剪力墙结构，建筑结构安全等级为二级。

本文将该标段中29号住宅楼作为案例进行研究，29号住宅楼为17层高层住宅，其中地上16层均为普通住宅楼，17层为跃层式住宅，建筑高度为54.90 m。单位工程建筑面积为12033.57 m2，基底面积为716.49 m2。

2.2基于VSM-GA的流程优化实施

图2　价值流现状图

(1) 收集数据并绘制价值流现状图与施工方案表

表1　施工工序方案表

通过对施工现场的实地考察，决定将研究重点集中在梁板柱的浇筑这一施工任务中，并实施了为期1个月的现场跟踪记录，并在此期间对项目经理、技术负责人以及施工班组成员进行了采访，获取了足够的相关数据并绘制了价值流现状图和施工工序方案表，如图2和表1所示。

(2)识别问题并确定基本目标函数

通过对价值流现状图的初步分析，将缩短施工时间、提高增值时间百分比、一次通过率与准时开工率作为需要改进的目标，设置的目标函数和约束函数如公式(12)所示，其权重系数ωk依次为1.2、1.15、1.08和1，修正系数φ为2.0。

(3)选择精益工具并构建效用系数矩阵

首先组建精益专家工作组，通过定性和定量分别筛选出拟采用的精益工具并构建效用系数矩阵如表2所示，而为了简化GA算法，可直接确定部分必须采用的精益工具。

在本案例中，拟采用的精益工具为标准化、KanBan管理、KanBIM管理、全面质量管理、并行工程、团队合作、持续改进、最后计划者体系、工作重组和先入先出原则。其中根据实际需求，将工作重组和先入先出(FIFO)设定为必须采用的精益工具。

表2　精益工具效用系数(以工序时长D为例)

(4)运行GA算法并输出最优组合方案

图3　每代进化过程中的最优目标函数值

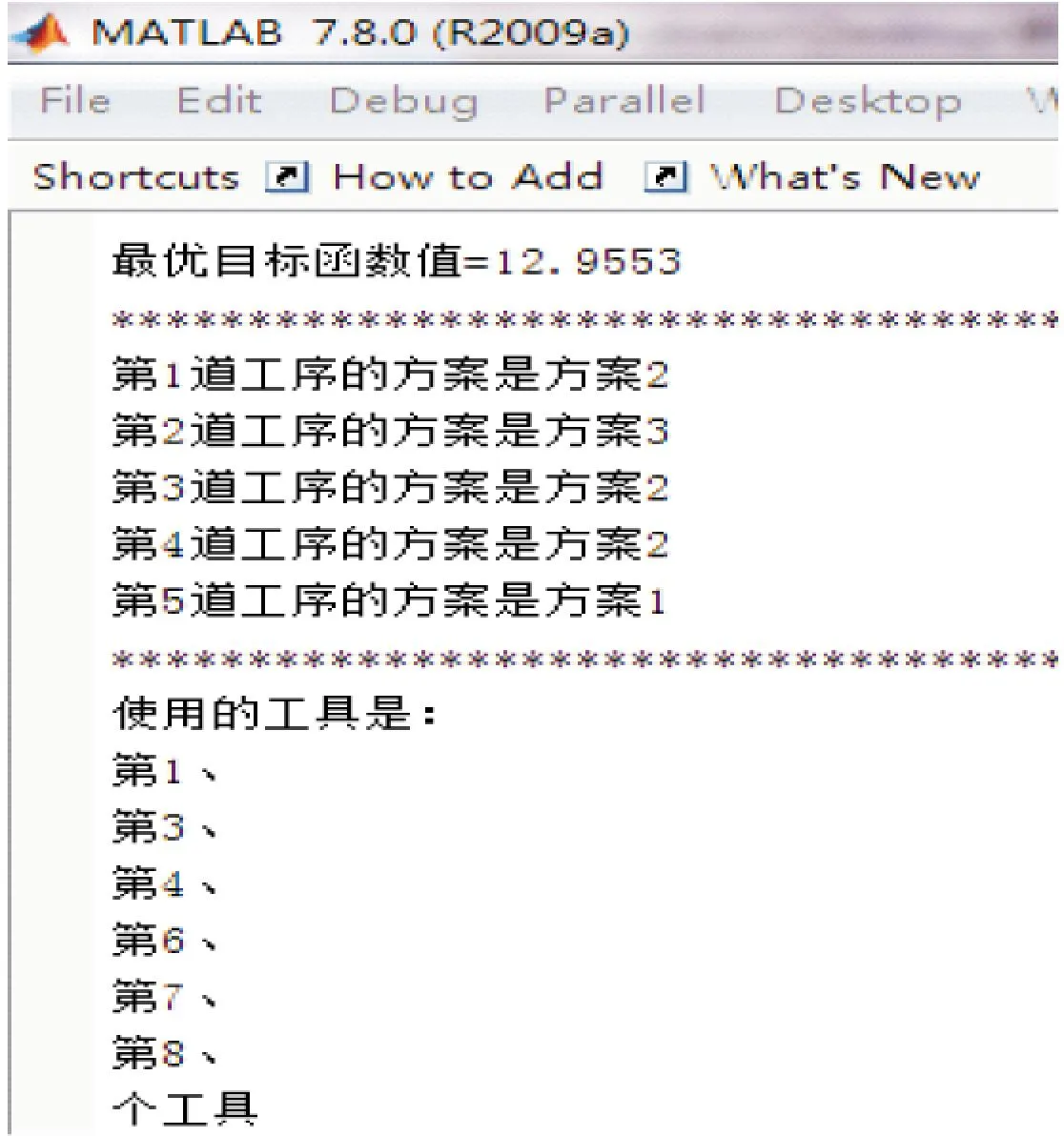
图4　最优方案组合

(5)最优组合方案的二次优化

根据GA算法输出的染色体可知，5道工序分别采用方案2、3、2、2、1且使用标准化、KanBIM管理、全面质量管理、团队合作、持续改进、最后计划者共6种精益工具。根据公式(15)和(16)可得各Wi和Vi，如表3所示。

表3　效用数值分析表

(6)绘制价值流未来图并实施精益计划

图5　价值流未来图

经过遗传算法优化后得到工序施工方案与精益工具的最优组合，根据优化结果绘制价值流未来图，如图5所示。其中，施工周期时间缩短了26%，各工序有效工作时间百分比均提高了约25%，各工序一次通过率达到了100%，各工序准时通过率也得到了不同程度的提升，特别是模板拆除工序的准时开工率提高了58%。通过二次优化结果可得，在使用精益工具对现浇梁板柱的工作价值流改进时，可以按照工作重组、先入先出原则、全面质量管理、KanBIM、标准化、最后计划者体系、持续改进、团队合作的顺序来实施改进计划；而在现浇梁板柱施工过程的各道工序中，应当加强管理Vi最大时所对应的工具，见表3。

3结语

在建筑产业现代化的时代背景下，提高施工效率、减少施工浪费必然是整个行业的追求，优化施工流程必然是达成目标的重要途径。价值流程图技术与遗传算法的有机整合使得施工流程优化实现了定性与定量的结合、主观与客观的统一，通过两阶段优化不但确定了最优方案组合，而且为精益改进计划的实施提供了指导，保证了价值流现状图向价值流未来图的转变。随着物联网与BIM技术的发展与成熟，提高了项目信息传输的准确性与实时性，将进一步实现基于VSM-GA的施工流程优化的动态与持续改进，促进建筑产业的现代化发展。

参考文献

[1]杨青, 王蕊. 基于价值流图析技术的研发项目绩效评价研究[J].管理学报, 2010, 7(4)： 619-623．

[2]Yu H, Tweed T, Al-Hussein M, et al. Development of lean model for house construction using value stream mapping[J]. Journal of Construction Engineering and Management, 2009, 135(8)：782-790

[3]Rosenbaum S, Toledo M, González V. Improving environmental and production performance in construction projects using value-stream mapping: case study[J]. Journal of Construction Engineering and Management, 2014, 140(2): 04013045.

[4]Gurumurthy A, Kodali R. Design of lean manufacturing systems using value stream mapping with simulation: a case study[J]. Journal of Manufacturing Technology Management, 2011, 22(4)： 444-473.

[5]Erikshammar J, Lu W, Stehn L, et al. Discrete event simulation enhanced value stream mapping: an industrialized construction case study[J]. Lean Construction Journal, 2013, 47-65.

[6]Faulkner W, Badurdeen F. Sustainable value stream mapping (Sus-VSM): methodology to visualize and assess manufacturing sustainability performance[J]. Journal of Cleaner Production, 2014, 85： 8-18.

[7]蒋书鸿, 苏振民.精益建造——一种先进的建造体系[J].基建优化, 2004, 25(3)： 11-16.

[8]雷英杰, 张善文.遗传算法工具箱及应用[M].西安：西安电子科技大学出版社, 2014.

[9]曹真, 苏振民.基于案例分析的精益建造应用实践研究[J].建筑经济, 2008, (10)：78-80.

[10]章蓓蓓, 苏振民, 金少军. 精益建造体系下项目流程管理研究[J].工业技术经济, 2008, 27(3)： 77-79.

Building Construction Process Optimization Based on VSM-GA

ZHONGJun-yi1,SUZhen-min1,SHEXiao-jie2

(1. School of Civil Engineering，Nanjing Technology University， Nanjing 211816， China；

2. Jiangsu Shuntong Construction Group Co Ltd， Nantong 226400， China)

Abstract:The issues about inefficient production, unstable process and serious waste of resources which existed in the progress of construction results in the poor benefit of construction and hinder the sustainable development of construction industry. Therefore, the optimization of the construction process is of great significance. This paper proposed an integrated framework of value stream mapping(VSM) and genetic algorithm (GA) where the digitization in merit function of GA makes up for the subjective arbitrariness of VSM in the program selection to optimize the construction process more effectively. Upon this basis, this paper built the objective optimization model of VSM-GA to achieve the optimum combination program of process optimization by setting up the objective function of process optimization, utility coefficient matrices of lean tools and multi-parameter and discrete-type operational rules of genetic algorithm. Finally, this paper further elaborated the VSM-GA-based construction process optimization implementation process and verified the feasibility and effectiveness of the model by case study.

Key words：process optimization； value stream； genetic algorithm； lean construction

中图分类号：TU721+.2

文献标识码：A

文章编号：2095-0985(2016)01-0103-07

作者简介：仲珺怡(1990-)，女，江苏苏州人，硕士研究生，研究方向为项目管理(Email：zjy1990sd@sina.com)

收稿日期：2015-08-31修回日期： 2015-10-21