DEA/TOPSIS模型在建筑材料供应商选择中的应用

袁永博，　刘丽霞，　张明媛

(大连理工大学　建设工程学部， 辽宁　大连　116024)



DEA/TOPSIS模型在建筑材料供应商选择中的应用

袁永博，刘丽霞，张明媛

(大连理工大学建设工程学部， 辽宁大连116024)

摘要：为了使建设项目中建筑材料供应商的选择更加合理，针对逼近理想解排序法(TOPSIS)逆序和数据包络分析(DEA)不能全排序等问题，本文将广义DEA与TOPSIS相结合，在建立建筑材料供应商评价指标体系的基础上，首先运用广义DEA中的G-C2R模型，从备选供应商中筛选出相对样本供应商有效的供应商，然后运用TOPSIS对有效的供应商进行排序，进而为决策提供依据。应用G-C2R/TOPSIS联合模型对供应商进行优劣排序，兼并了G-C2R的样本集选择任意性和TOPSIS方法的灵活性以及计算简单等特点。本文还用案例证明了TOPSIS逆序问题的存在，以及DEA/TOPSIS联合模型能够通过筛选和排除相对无效供应商来减少TOPSIS逆序问题对决策产生的影响，因此联合模型可以为建筑材料供应商的选择提供可借鉴的科学依据。

关键词：建筑材料；供应商选择；数据包络分析；逼近理想解排序法

供应商选择问题一直是供应链研究中的热点，对供应商的评价与选择是供应链中的一个重要环节，也是供应链管理的重要内容。在建设工程项目中，建筑材料成本约占建筑施工总成本的50%～70%[1]，而且供应材料的质量以及供应是否准时也将直接影响整个工程的质量和工期。因此，采用科学合理的方法来进行建筑材料供应商的选择与评价，评选出最合理、最有竞争力的供应商是非常必要的。

目前，越来越多的评价模型应用到建筑材料供应商选择中，其中TOPSIS模型在建筑材料供应商的选择中应用比较广泛，这是因为其具有应用灵活，数学计算简单，结果量化客观等优点。并且研究者们对其做了不少的改进，主要集中在对TOPSIS模型权重计算的优化上，包括熵权与TOPSIS结合[2,3]，ANP与TOPSIS结合[4]，AHP与TOPSIS结合，粗糙集与TOPSIS集合[5]，模糊集与TOPSIS结合[6]等。但是在这些研究中，并没有考虑到TOPSIS的逆序问题。与此同时，用于生产效率评价的DEA模型也开始运用到供应商的选择中，实现了计算权重[7]，方案筛选[8]，方案全排序[9]等功能。

文献调查过程中发现，DEA模型虽然在方案全排序方面没有比TOPSIS更有优势，但是其筛选功能可以用于减小决策环境变化对决策的影响。本文将DEA模型与TOPSIS相结合，采用DEA模型对决策方案(即决策单元，供应商的选择中体现为候选供应商)进行筛选，然后用TOPSIS进行排序，形成了一套新的建筑材料供应商评价的方法。

1建筑材料供应商评价指标体系

影响供应商选择的因素很多，包括产品价格、质量、交货、企业环境等。在现有的研究文献[1,3,9～14]中，建筑材料供应商的评价指标通常包括质量、成本、交货等，详见表1。在构建建筑材料供应商综合评价指标体系时，需要遵循目的性、科学可比性、灵活使用性、系统全面简洁、定性与定量相结合、可拓展性等原则[13]，同时还需结合建筑施工企业材料管理的实际情况。根据这些原则，本文选择易于度量、数据采集方便、符合我国建筑业实际的供应商评价指标，即产品质量和成本、交货、生产能力、财务状况、服务水平，依次用产品合格率(C1)、产品综合成本(C2)、准时交货率(C3)、产量(C4)、资产负债率(C5)、投诉响应率(投诉响应率C6=获得解决的投诉事件数/投诉总数)来描述。其中，产品合格率、准时交货率、产量、投诉响应率属于效益型指标，产品综合成本、资产负债率属于成本型指标。

表1　供应商评价指标与描述统计

2G-DEA和TOPSIS方法

2.1G-DEA方法

DEA模型的经济解释主要基于经济学的生产函数理论，用有效生产前沿面来模拟生产函数。因此，它给出的效率值反映的是被评价单元相对于优秀单元的信息。但是在现实中，许多问题的评价参考集并不仅限于此。马占新[15]提出了一种更具广泛含义的DEA方法，不仅具有传统DEA方法的全部性质，而且还能依据任意参考集进行评价(如图1所示，DMU为决策单元)，将这种方法称为广义DEA方法，简称G-DEA。

图1　广义DEA可评价问题的范围

G-DEA方法在样本集上的突破，使得该方法适用范围更广。G-DEA可以通过自主选择参考集合来提供决策者希望获得的信息，而且可以依据不同的参考集进行评价。

G-DEA综合模型为Sam-C2WY，根据其中参数δ1、δ2、δ3取0，1可以得到G-C2R、G-BC2等模型[15]。综合各模型的优缺点，并结合建设材料供应商的特点，这里选择G-C2R模型。其中，成本型指标产品综合成本、资产负债率作为输入变量，效益型指标产品合格率、准时交货率、产量、服务水平作为输出变量。

G-C2R可表述为：

(1)

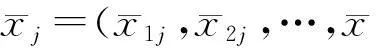
有效判断条件：存在ω0﹥0，μ0﹥0使得V(d)=1，或者V(d)﹥1。当d=1时，记G-C2R(1)弱有效为G-DEA弱有效，G-C2R(1)有效为G-C2R有效。

利用G-C2R模型可以对多个供应商多指标进行评价，从中选出相对样本有效的供应商，淘汰相对样本无效的供应商，从而为决策者提供客观的决策依据。但是G-C2R只能给出决策单元的相对有效性，并不能对各个决策单元进行全排序。有时会同时出现多个相对有效的决策单元，因此要想对决策单元进行完全的排序，就需要借助于其他的科学工具[16]。

2.2TOPSIS排序

TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution )方法是C L Hwang和K Yoon于1981年首次提出的一种多属性决策方法，其根据待评价方案与理想化目标的相对接近度进行排序，对方案的相对优劣进行评价。TOPSIS方法是多属性决策分析中一种常用的有效方法，又称为优劣解距离法[2]。

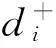
TOPSIS的一般步骤为：

(1)建立评价指标集合，指标标准化

当有n个指标，m个方案时，评价矩阵为：

(2)

(2)建立加权评价矩阵V，权重向量W=(w1，w2，…，wm)

V=R×W=

(3)确定理想最优解和最劣解

(4)计算综合距离，按相对接近度进行排序

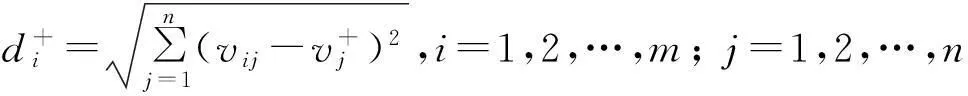
TOPSIS具有应用灵活，数学计算比较简单，结果量化客观等优点，但是TOPSIS等理想点决策方法会产生逆序，其原因是决策时选用了相对理想点。虽然引用绝对理想点可以实现强保序[17]，但要选择科学合理的绝对理想点是十分困难的，要实现强保序也并不容易。因此，选择一种筛选模型与TOPSIS相结合，通过筛选来降低逆序对决策的影响很有意义。

2.3GDEA/TOPSIS联合模型

运用TOPSIS模型求解多属性决策问题时，由于决策方案的增加或减少引起了决策环境的变化，有可能导致决策结果出现逆序现象。因此，通过对决策方案进行筛选，将排名靠后、指标值差的方案先排除，可以让决策环境更合理，避免一些排名靠后、指标值差的方案对最后的决策产生影响。

TOPSIS能进行全排序，但是在排序之前需要方案进行筛选；G-C2R能进行筛选，但是在全排序方面没有TOPSIS好。因此将G-C2R与TOPSIS相结合，减少TOPSIS中的逆序问题对决策产生的影响，同时实现优选方案的全排序，为决策提供依据。将此方法记为GDEA/TOPSIS联合模型，其原理为先采用G-C2R模型对决策方案(即G-C2R中的决策单元，在供应商的选择中体现为候选供应商)进行筛选，然后用TOPSIS进行排序。

GDEA/TOPSIS模型可分为五个阶段：

(1)确定建筑材料供应商评价指标体系；

(2)确定获准供应商，对获准供应商各指标进行评分；

(3)确定筛选样本，样本可以是待选供应商里较好的供应商，也可以是承包商给定各项指标值的理想供应商。通过G-C2R用优先供应商样本对获准供应商进行筛选得到优先供应商，运用模型G-C2R计算；

(4)TOPSIS对优先供应商进行排序，运用模型TOPSIS计算；

(5)根据项目情况选择供应商，从最优供应商开始选择。

3算例分析

3.1案例背景

某建筑企业需要在10个原材料供应商中选择一个合作伙伴，确定的评价指标为产品质量和成本、交货、生产能力、财务状况、服务水平，依次用产品合格率C1、产品综合单位成本C2、准时交货率C3、产量C4、资产负债率C5、投诉响应率C6来描述。

通过测定和估算，收集各供应商的指标评价值，如表2所示。

表2　原材料供应商的评价指标值

3.2G-C2R模型筛选

案例中输入变量产品综合成本、资产负率，分别对应x1，x2，输出变量产品合格率、准时交货率、产量、服务水平，分别对应y1，y2，y3，y4。

以供应商A1、A3为样本，供应商A1、A2、A3、A4、A5、A6、A7、A8、A9、A10为决策单元，运用G-C2R模型进行运算，以存在ω0﹥0，μ0﹥0使得V(d)=1，或者V(d)﹥1为有效判定条件，将无效的供应商淘汰。当A1为决策变量时，G-C2R模型为：

MaxV(d)=97μ1+96μ2+439μ3+97μ4

s.t.3650ω1+62ω2-97μ1-96μ2-439μ3-97μ4≥0

3620ω1+61ω2-98μ1-94μ2-450μ3-94μ4≥0

3650ω1+62ω2=1

ω≥0,μ≥0

解得ω1=0.000272，ω2=0，μ1=0，μ2=0，μ3=0.002252，V(d)=1，符合有效判定条件因而供应商A1有效。将决策变量A1、A2、A3、A4、A5、A6、A7、A8、A9、A10分别代入模型，得到各供应商相对样本A1、A3的效率值，如表3所示。从表3中可以判断出A2、A5、A7和A10为相对无效的供应商。

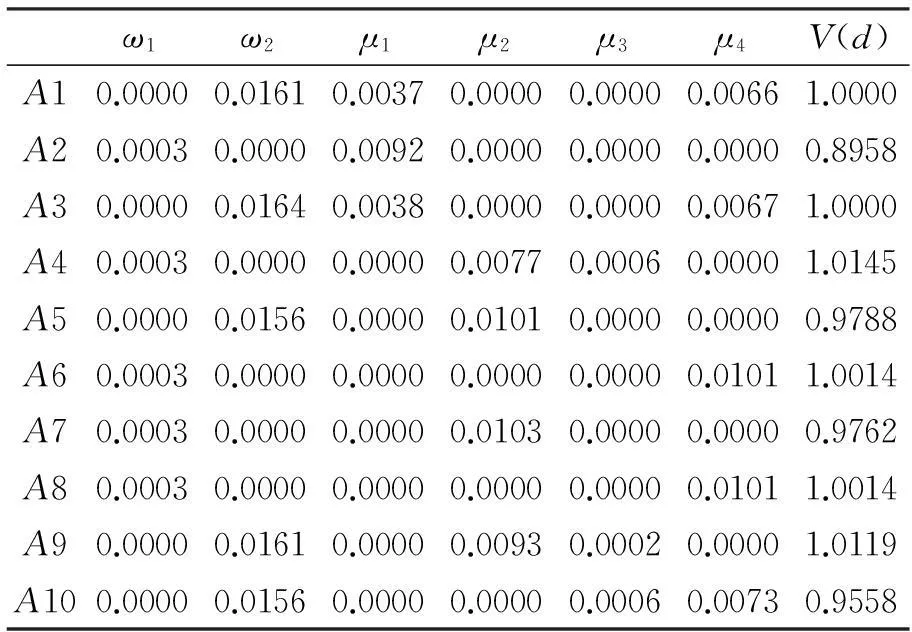
表3　效率值统计表

3.3TOPSIS排序

将输入输出变量数据标准化之后得到标准化数据矩阵。利用熵权法计算各指标的权重W=(0.014945，0.145116，0.096072，0.188266，0.275394，0.219388)T，计算得到加权数据矩阵如表4所示。根据各供应商的评价值与理想最优解和最劣想解的距离d+和d-，计算得到各供应商与理想最优解和最劣想解的相对接近度C，如表5～7所示。

根据表5排序为排序1：A8、A1、A6、A9、A3、A4、A10、A5、A7、A2。排除相对无效供应A2、A7和A10得到改进计算结果1，如表6所示。根据表6新的排序为排序2：A9、A1、A3、A8、A6、A4、A5。在表6的基础上排除相对无效的供应商A5，得到改进计算结果2，如表7所示。根据表7的排序为排序3：A1、A9、A3、A8、A6、A4。将排序1、排序2和排序3汇总，如图2所示，图2中用箭头分别标出了A1、A8和A9的排名变化，虚线框内为筛选出来的相对无效供应商。

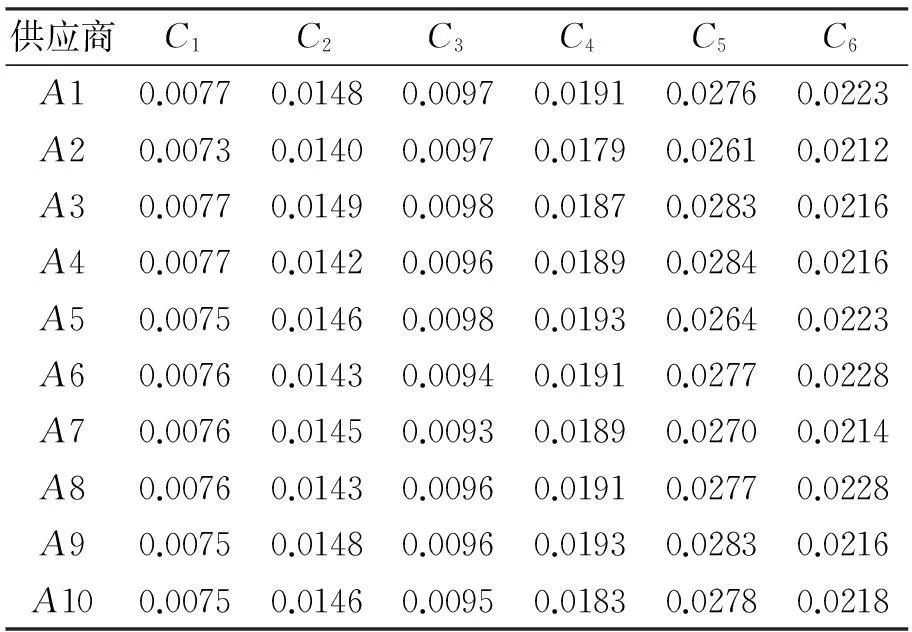
表4　加权数据矩阵

表5　原始计算结果

表6　改进计算结果1

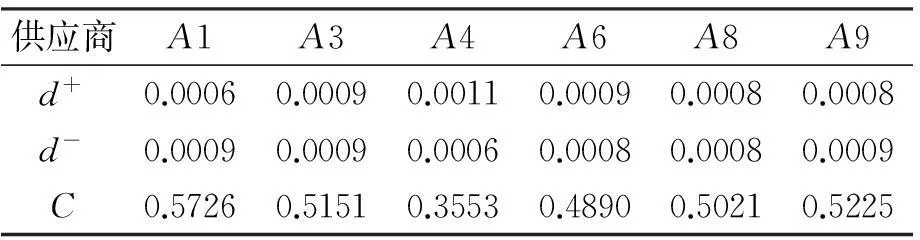
表7　改进计算结果2

图2　排序汇总

3.4计算结果分析

观察图2发现箭头有交叉，这表明有在不同排序中，A1、A8和A9排名前后发生了变化，并且排在第一位的供应商从A8变成A9，最后变成A1。此现象证明TOPSIS确实存在逆序问题，而且逆序会影响最后的决策。G-C2R模型筛选出来的相对无效的供应商A2、A5、A7和A10在原始排序(表5和图2所示)中的后4位，且A2、A5、A7和A10的相对接近度分别为0.1079、0.4886、0.4180、0.5585，比其他的供应商差很多。比较排序1、2、3(如图2所示)发现A2、A5、A7和A10是否参与排序会对最后的相对接近度排序产生影响，进而影响决策。所以在运用TOPSIS模型进行优选排序时，先对样本进行筛选是有必要的，G-C2R筛选出来的相对无效供应商在原排序中靠后，将其删除进行重排序的结果更具有参考价值。

改进后的G-C2R/TOPSIS联合模型通过筛选淘汰掉相对无效的供应商，可以在一定程度上优化决策环境，进而减少决策环境对决策造成的不利影响。

4结语

科学合理地选择建设项目建筑材料供应商是实现项目管理三大目标十分重要的一个环节。本文在构建建筑企业供应商选择指标体系的基础上，应用G-C2R/TOPSIS联合模型对供应商进行优劣排序，兼并了G-C2R的样本集选择任意性和TOPSIS方法的灵活性以及计算简单等特点，减少了TOPSIS模型逆序问题对决策产生的影响，提高了选择评价过程的科学性和合理性，具有一定的实际意义。

参考文献

[1]张燕超. 基于改进TOPSIS法的材料供应商选择评价研究[J]. 物流科技, 2014, 37(2): 98-101.

[2]陈雷, 王延章. 基于熵权系数与TOPSIS集成评价决策方法的研究[J]. 控制与决策, 2003, 18(4): 456-459.

[3]彭频, 李静. 基于熵权TOPSIS的建筑供应商选择问题研究[J]. 江西理工大学学报, 2010, 31(2): 67-69.

[4]陈威威. 基于ANP/TOPSIS的战略伙伴型建材供应商选择[J]. 土木工程与管理学报, 2013, 30(2): 90-94.

[5]陈红梅. 基于粗糙集的TOPSIS供应链合作伙伴选择[J]. 统计与决策, 2011, (22): 178-180.

[6]Liao C N, Kao H P. An integrated fuzzy TOPSIS and MCGP approach to supplier selection in supply chain management[J]. Expert Systems with Applications, 2011, 38(9): 10803-10811.

[7]郑斌, 刘凤国. 重视熵权的供应商选择DEA/TOPSIS联合方法[J]. 工业工程, 2011, 14(6): 55-59.

[8]Chen Y J. Structured methodology for supplier selection and evaluation in a supply chain[J]. Information Sciences, 2011, 181(9): 1651-1670.

[9]颜波, 石平. 基于超效率DEA模型的绿色供应链环境下供应商评价与选择[J]. 统计与决策, 2013, (13): 37-40.

[10]祝博. 工程材料供应商选择研究[D]. 大连: 大连海事大学, 2008.

[11]谢玖琪, 林涛, 王杰. 基于熵权和TOPSIS法对工程材料供应商选择的评价研究[J]. 价值工程, 2010, 29(12): 49-50.

[12]黄洁, 刘发全. 基于粗糙集的建筑材料供应商选择方法[J]. 物流技术, 2005, (1): 48-50.

[13]王军武, 呙淑文. 基于灰色关联度的建筑供应商选择方法研究[J]. 武汉理工大学学报, 2007, 29(3): 153-156.

[14]马玉国, 舒欢. 工程项目物资供应商选择研究[J]. 工程管理学报, 2014, 28(1): 93-97.

[15]马占新. 一种基于样本前沿面的综合评价方法[J]. 内蒙古大学学报(自然科学版), 2002, 33(6): 606-610.

[16]于泽, 王林秀. 供应链环境下建筑材料供应商选择问题研究[J]. 现代贸易工业, 2010, (4): 3-5.

[17]黄德才, 郑河荣. 理想点决策方法的逆序问题与逆序的消除[J]. 系统工程与电子技术, 2001, 23(12): 80-83.

Material Supplier Selection in Construction Based on DEA and TOPSIS

YUANYong-bo,LIULi-xia,ZHANGMing-yuan

(Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract:In order to select a material supplier in construction project scientifically, and considering the rank reversal of order preference by similarity to ideal solution (TOPSIS) model and data envelopment analysis model (DEA) is unable to order totally，this paper combined generalized DEA and TOPSIS, based on establishing supplier evaluation index system, selected G-C2R model of generalized DEA to screen effective suppliers from alternative suppliers, then order them by TOPSIS. It has the merits of two methods to order the suppliers by the DEA/TOPSIS model, including the G-C2R’s randomness of selecting sample set and the flexibility of TOPSIS. A case demonstrated the existence of the rank reversal of TOPSIS, and proved that the combined model (DEA/TOPSIS) can decrease the effect of the rank reversal of TOPSIS through eliminating relative ineffective suppliers. Therefore, the combined model can provide a scientific basis for material supplier selection in construction project.

Key words：building material; supplier selection; DEA; TOPSIS

中图分类号：F274; F224

文献标识码：A

文章编号：2095-0985(2016)01-0007-05

作者简介：袁永博(1957-)，男，辽宁大连人，教授，博士，研究方向为现代信息技术在工程项目管理中的应用及建设项目全寿命周期评估(Email：yongbo@dlut.edu.cn)

收稿日期：2015-09-08修回日期： 2015-09-28