基于PCA—C-OWA算子赋权的钢筋混凝土施工质量灰色聚类评价

陈为公，　张胜昔，　王会会

(青岛理工大学　管理学院， 山东　青岛　266520)



基于PCA—C-OWA算子赋权的钢筋混凝土施工质量灰色聚类评价

陈为公，张胜昔，王会会

(青岛理工大学管理学院， 山东青岛266520)

摘要：钢筋混凝土结构凭借其整体性强、稳定性高、耐久性好等优势，已逐渐成为建设工程项目中普遍采用的结构形式。而钢筋混凝土的施工质量是影响建筑物耐久性和安全性的主要因素，其优劣程度直接关系到建设工程项目整体质量水平。针对钢筋混凝土施工质量所受影响因素众多，具有模糊、灰性等不确定性特征，基于科学、真实、可操作等原则，提出影响钢筋混凝土质量的要素集，并对集合的26个要素进行PCA降维，对得到的10个主成分结合工程实践经验进行归纳分析，构建了钢筋混凝土施工质量评价指标体系。利用C-OWA算子对指标进行客观赋权，并结合灰色聚类评价模型进行评价，由此得到针对模糊性和灰性的客观质量水平。最终，通过实证研究验证了该评价方法的有效性。

关键词：钢筋混凝土；施工质量；主成分分析；C-OWA算子；灰色聚类评价

自1813年法国Vicant I J发明混凝土以来，该技术便在全球范围内迅速传播。截至目前，钢筋混凝土已成为我国结构施工中主要的应用材料，因此其质量是影响结构安全性、适用性、耐久性的关键问题。随着建设工程逐渐趋于大型化、复杂化，钢筋混凝土施工作为与工程整体质量相关的重要环节，其施工质量的要求越来越高，质量的模糊、灰色等不确定性问题却始终没有得到解决。因此对钢筋混凝土进行系统、综合的评价具有非常重要的现实意义。针对混凝土的施工质量问题，国家已经制定了大量相关施工质量管理规范和标准。在此基础上，众多学者对于钢筋混凝土施工质量进行了更为深入的研究。李亚平，陈勇等[1,2]建立了基于混凝土缺陷评价的模糊综合评判模型。郑少瑛等[3]利用神经网络方法建立混凝土施工质量评价的模拟模型；徐莉丽等[4]确定了影响钢筋混凝土构件质量14个影响因素，基于质量问题的模糊性，建立了基于F-AHP的钢筋混凝土质量的综合评价模型。孟令星等[5]将层次分析法(AHP)与熵值法相结合共同确定指标权重，并对钢筋混凝土工程的施工质量进行了可行的评价。经大量研究发现，虽然混凝土质量研究涉及的范围广泛，方法众多，然而如何将质量科学进行科学量化，始终是质量评价研究难以彻底解决的难题。在质量评价方面针对于质量的模糊不确定性研究相对集中，然而很少考虑到施工质量的灰性存在，由此进行的质量评价研究，也缺乏一定的客观合理性。鉴于此，本文在考虑混凝土施工质量模糊性的同时引入灰色系统理论，科学实现了质量的定量化研究，辨证的对施工质量进行更加客观有效的评价。

1施工质量评价指标体系构建

1.1评价指标的确定

根据钢筋混凝土施工的工程实际经验，采用德尔菲法进行调研，得到钢筋混凝土施工质量评价要素指标，如表1。

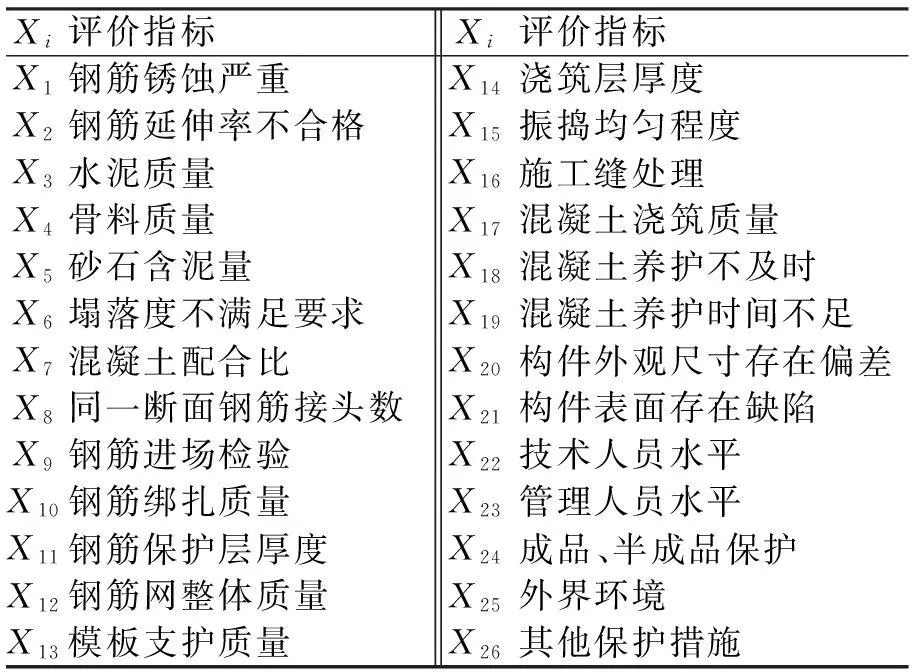
表1　钢筋混凝土施工质量评价要素集

1.2数据的采集与处理

将各因素对目标的影响程度划分为较低、一般、严重、很严重4个等级，满分10分。具体评分表如表2所示。

表2　要素等级评分表

选择15位相关专家与20位同行从业人员进行调研，根据回收情况筛选出30份有效样本。整理得评价矩阵Xij，其中i为评价因素个数，此处i=26；j为样本数，此处j=30。运用SPSS 20.0进行处理数据，得到方差贡献率、累计方差贡献率和主成分荷载，并计算得到主成分特征向量。具体见表 3。

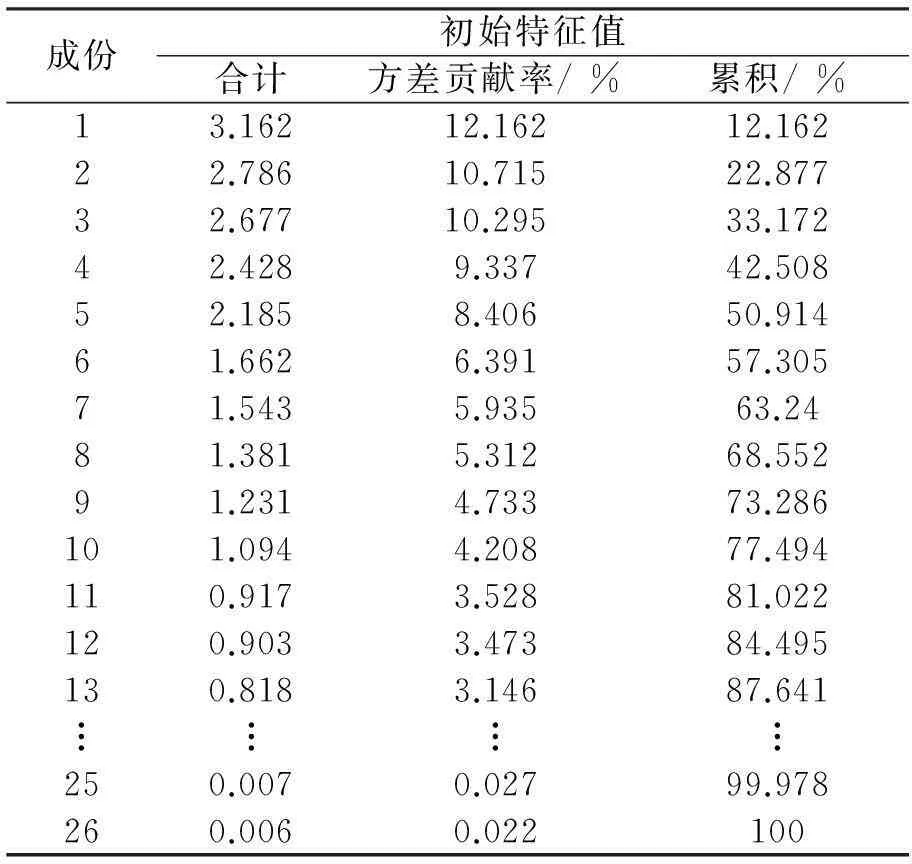
表3　解释的总方差

1.3提取主成分

根据特征值大于1原则得到主成分个数g=10，由此时方差累计贡献率77.494%可以看出，这10个主成分在所有成分中代表性强、含有信息量大。选取主成分Y1,Y2,…,Yg，则主成表达式为：Yg=ug1zg1+ug2zg2+…+ugpzgp；其中p=26，u为主成分特征向量；z用以表达主成份的评价要素。

由SPSS 20.0可以得到主成分特征向量，具体数据见表4。

1.4主成分数据分析

表4中的主成分系数，数值越大说明对主成分影响度越大，因此应选择对应系数值较大指标作为反映主成分主要指标。根据要素的对目标的影响程度，对主成分进行归纳：

表示主成分Y1线性关系的系数u1中X2,X4,X8的系数的绝对值分别为0.314、0.375、0.375，相对于其他指标的系数较大，因此X2,X4,X8为表示Y1的主要成分，而这三个指标分别对应“钢筋延伸率不合格”、“骨料质量”和“同一断面钢筋接头数”，反映的是原材料质量和钢筋制作安装。与Y1原理相同，可得到反映其他主成分的主要因素，并归纳该主成分主要反映的内容：Y2主要用X6,X11,X16,X20表示，反映的是原材料质量和施工技术；Y3主要被X3,X7,X12,X22表示，反映的是原材料质量和施工技术人员水平；Y4主要被X9表示，反映钢筋质量；Y5主要被X6,X13,X17,X19,X26表示，反映原材料质量、混凝土施工及养护；Y6主要被X9,X16,X25表示，反映钢筋质量和施工工艺；Y7主要被X13,X15,X25表示，记为混凝土浇筑和受环境影响；Y8主要被X21,X23,X24表示，记为模板支护和混凝土养护；Y9主要被X20,X24表示，记为混凝土表面质量；Y10主要被X2,X5,X20表示，记为原材料质量及施工工艺。

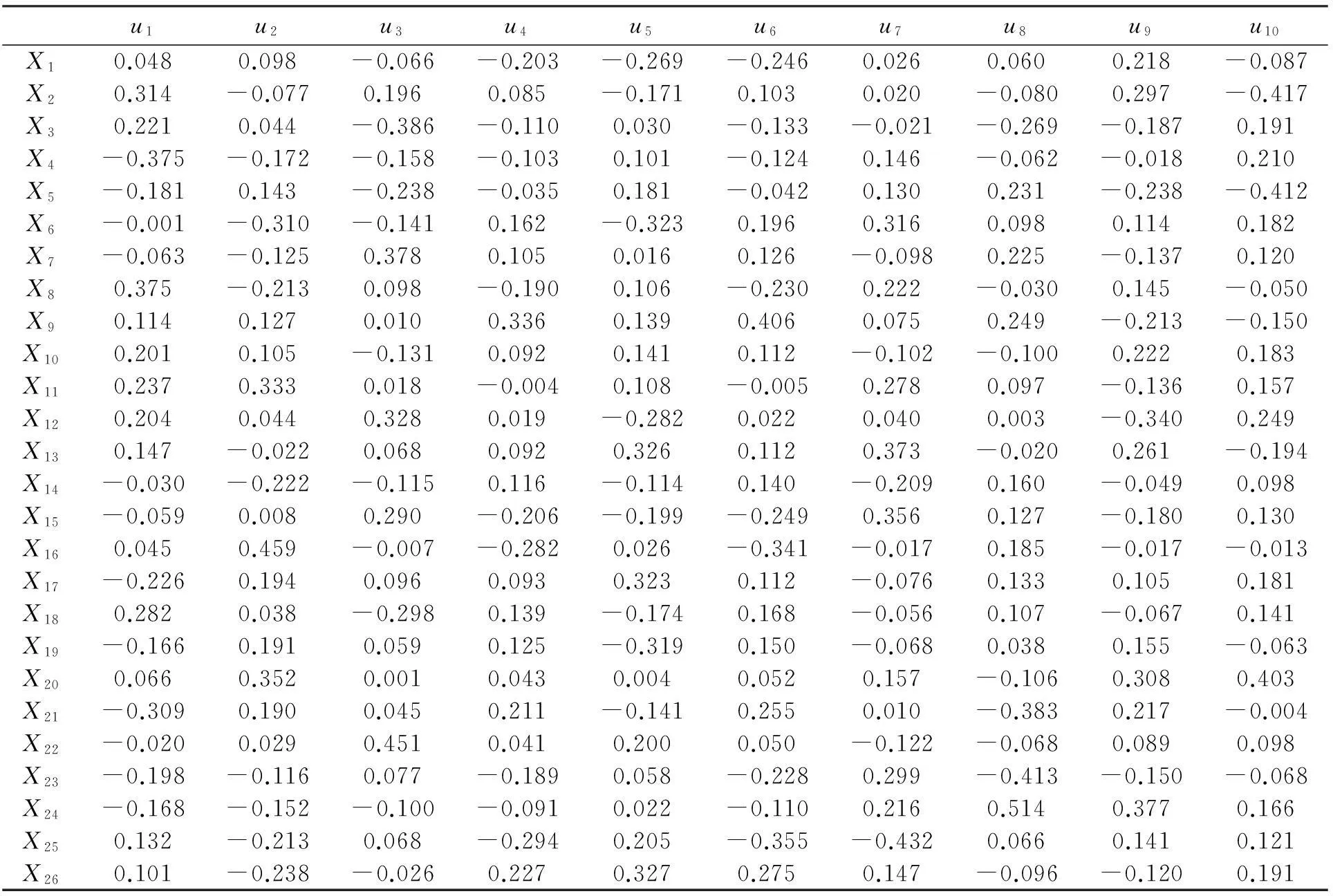
表4　主成分特征向量

1.5指标体系构建

上文对主成分进行了归纳分析，分析各要素在主成分中的作用，再结合工程实际，并参考钢筋混凝土施工质量评价相关文献[1～6]，对主成分进行系统分类重组：其中Y1,Y2,Y3,Y5均反映出了原材料质量，故将原材料质量作为评价指标1，记为A1；Y1,Y2,Y3,Y6,Y7,Y8,Y10所反映的指标均与施工工艺有很强的关联性，故将施工过程工艺作为评价指标2，记为A2；Y5,Y8,Y9均反映出混凝土养护的重要性，故将混凝土养护质量作为指标3，记为A3；各主成分均受到管理水平与环境影响，且环境影响在Y7中有重要反映，故将管理水平与受环境影响作为指标4，记为A4。

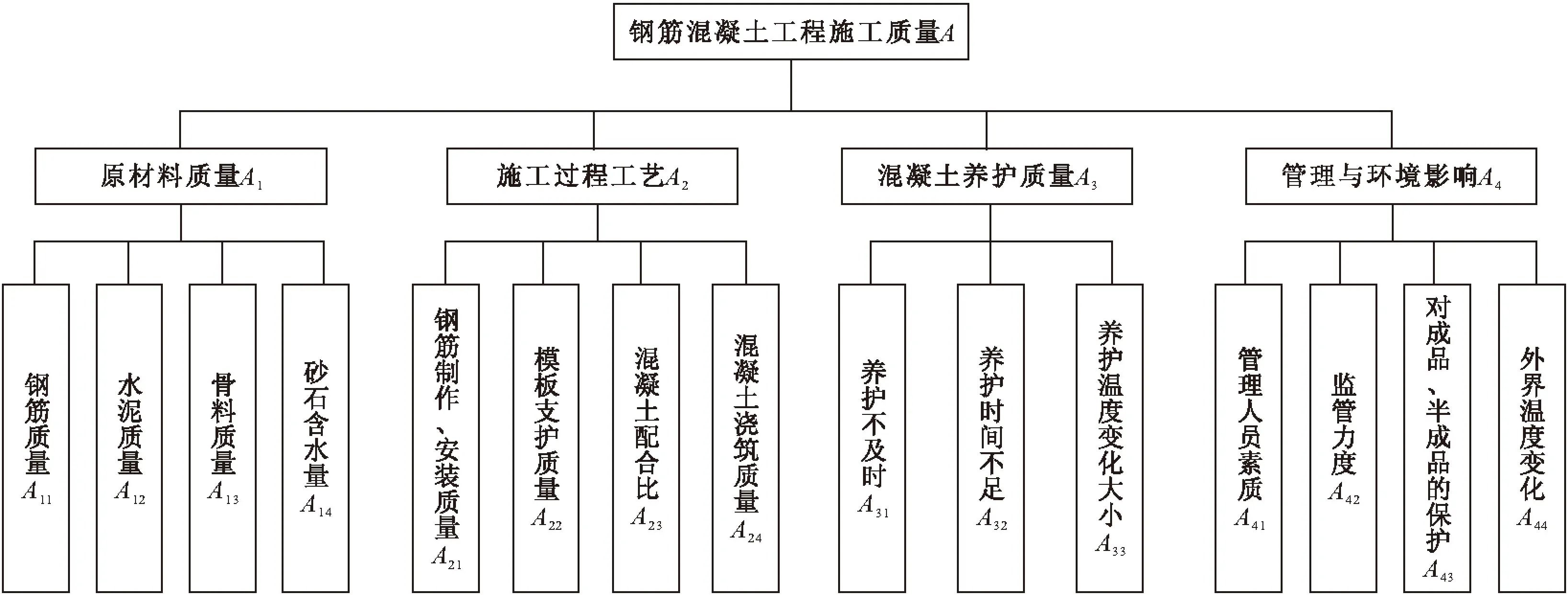
图1　钢筋混凝土施工质量评价指标体系

继续对确定的指标进行质量域的划分与分层，构建了层次分明的指标体系，如图1。

2基于C-OWA算子赋权法确定指标权重

OWA[6,7]算子作为最重要的累计算子，其本质在于元素的递增排列及权重只与位置有关，自1988年由Yager教授提出以来得到了广泛的研究。我国学者从改进数据集结形式的角度，提出了众多变化的OWA算子[8,9]，本文运用的是一种基于组合数改进加权向量以实现科学加权计算的组合数有序加权算子(Combination ordered weighted averaging，C-OWA)[10]。

赋权步骤如下：

(1)指标A的决策数据集结为(a1,a2,…,ai,…,an)，将数据重新从大到小排列并从0开始编号，得重新集结的数列b0≥b1≥b2≥…bj≥…bn-1即(b1,b2,…,bi,…,bn)；

(2)用组合数设计数据的权重，得加权向量：

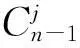
(2)

(4)计算指标Ai的相对权重值ωi：

(3)

通过上述运算，即可完成对指标体系的赋权。

3钢筋混凝土质量灰色聚类评价

3.1钢筋混凝土质量的测度界定

混凝土施工过程中影响因素多、产生的信息量庞大，与之相随的信息沟通模式却并没有得到有效改进，造成了信息传播过程中的失真，甚至丢失现象。而对其进行的质量评价是评价质量目标是否在到合格或良好范围之内，而这个范围本身就是一个灰概念，其外延是很清楚的，但如果要问到底达到合格或良好内的哪一个具体数值，却很不明确。

为将质量定量化，根据工程实践经验对钢筋混凝土质量进行测度界定，从统计学的角度来讲，对质量进行评价之前，得到的质量评价结果在概率理论上是等同的，故将界定的测度均等划分。同时从提高质量管理水平的角度出发，应将最高级别的界定测度尽量提高，扩大测度取值范围，以减小最低级别质量测度界定难度，从而提高质量评价的科学性。

设定质量测度取值范围为[0,10]，分为：优、良好、合格、差、极差共5个等级，具体界定如表5所示。

表5　钢筋混凝土质量测度

3.2基于三角白化权函数的灰色聚类评价模型

灰色系统理论方法[11]，是对系统论、信息论、控制论的观点和方法的延伸，模型简单明了、概念清晰、宜于应用且结论可靠的特点。灰色聚类评估模型作为其中经典的评价方法，通过数理模型将灰色系统转换为白色系统，从而得到可供分析的评价结果。

3.2.1灰类的确定及对应白化权函数的建立

灰色系统理论研究学者刘思峰提出了中心点三角白化权函数模型，对数据灰类的所属情况进行描述[12]。确定“优、良好、合格、差、极差”五个灰类，中心点向量为U=(9,7,5,3,1)，根据混凝土质量评价内涵建立各灰类对应的白化权函数[13]，具体见表6。

表6　各灰类及对应的白化权函数

注：dijk为第k个专家对第i个指标下的第j个分指标所赋的值，k=1,2,…,p。

3.2.2灰色聚类评估步骤

(1)建立评价矩阵。按界定的质量测度，请p个专家对指标Aij进行赋值，建立评价矩阵Di=[dijk]s×p，其中s为矩阵的评价指标的数量。

(4)

(3)合成聚类评价矩阵。对各初级指标聚类评价：

Zi=ωi·Ri

(5)

构造上级指标的综合评价矩阵Z0=[Z1,Z2,…,Zn]T，再进行上层指标的综合聚类评价：

M=ω0·Z0=[M1,M2,…,Mn]

(6)

(4)计算各级指标评价值。为避免根据传统最大权原则确定灰类时导致信息丢失，将综合评价向量与测度阀值进行合成，做单值化处理W=M·U(其中U为测度阀值)，获得钢筋混凝土质量综合评价值。

4实证分析

采用C-OWA算子与灰色聚类评价相结合的方法对钢筋混凝土施工质量进行定量评价，为进行科学的质量管理与决策提供依据。现以某工程项目为例进行实证研究。

4.1基于C-OWA算子确定权重

以二级指标为例，邀请专家进行赋权评分，如表3所示：

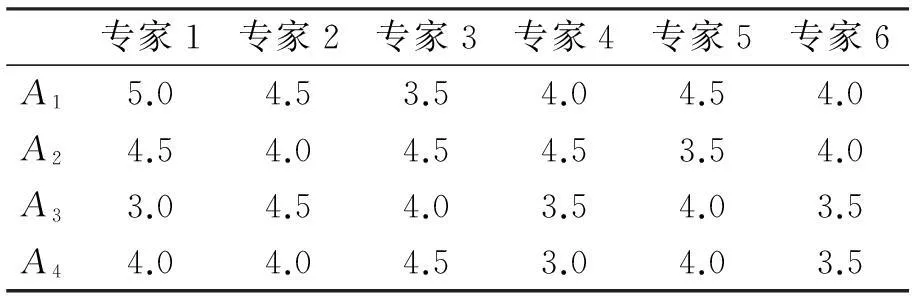
表7　指标权重评分决策数据

将决策数据按由大到小顺序进行排列得bi=(5.0,4.5,4.5,4.0,4.0,3.5)；因n=6，可根据(1)计算赋权向量：

wj=(0.03125,0.15625,0.3125,0.3125,0.15625,0.03125)

则根据式(2)计算A1的绝对权重：

同理可得：

根据式(3)计算二级指标权重向量为：

ω0=(0.263,0.262,0.232,0.242)

各三级评价指标权重向量的确定同上，分别为：

ω1=(0.273,0.269,0.230,0.228)

ω2=(0.260,0.212,0.216,0.312)

ω3=(0.291,0.354,0.355)

ω4=(0.252,0.254,0.264,0.230)

4.2灰色聚类评价

邀请专家对A1～A4进行赋值，根据各类灰数及对应灰类，构造评价矩阵Di=[dijk]s×p如下：

根据表6和式(4)得到灰色聚类权矩阵Ri：

根据式(5)，将权重向量与灰色聚类权矩阵合成，得综合灰色聚类评价矩阵Z：

Zi=ωi·Ri

根据式(6)得综合评价向量M：

M=ω0·Z0=[0.377,0.390,0.234,0.012,0.000]

将综合评价向量M与测度阀值U=(9,7,5,3,1)合成，计算钢筋混凝土质量评价值W，W=M·U=7.329，由质量测度表可知，综合质量评价值为良好，未达到优秀等级。

同理即可计算二级指标的质量综合评价值：W1=7.343，W2=7.461，W3=7.269，W4=7.227对指标质量值从小到大排序W4

5结论

(1)通过PCA多元回归方法构建钢筋混凝土施工质量评价指标体系，避免了根据主观经验直接确定指标的主观弊端，使得构建的指标体系更加科学合理。

(2)基于C-OWA算子赋权具有削弱评价数据极端值带来的不利影响，使得指标赋权更加合理。结合灰色聚类评价模型，不仅可以将所有评价数据反应到评价结果中，而且充分应对了钢筋混凝土质量的灰色性。

(3)通过本文的模型对算例进行评价可知，该项目各钢筋混凝土的施工质量指标值由小到大排列依次为管理与环境、混凝土养护、混凝土施工和原材料质量，其中前两者，通过权重计算发现对总体质量的影响较低，但是质量最终评价结果相对较差，应引起管理者重视。

参考文献

[1]李亚平. 采用模糊综合评判法评定混凝土缺陷的研究[J]. 工业安全与防尘, 1998, (1): 38-41.

[2]陈勇, 何飞. 基桩混凝土质量模糊综合评价研究[J]. 中外公路, 2009, 29(3): 36-39.

[3]郑少瑛, 周东明, 许婷华, 等. 人工神经网络在混凝土施工质量评价中的应用研究[J]. 混凝土, 2008, 35(4): 120-122.

[4]徐莉丽, 肖正学, 苏有文. 钢筋混凝土构件质量综合评价的F-AHP模型[J]. 福建建设科技, 2010, (6): 17-18.

[5]孟令星, 谢广采, 付建明. 基于AHP与熵权的钢筋混凝土工程施工质量评价[J]. 工程建设, 2012, 44 (5): 69-73.

[6]Yager R R. Families of OWA operators[J]. Fuzzy Sets and System, 1993, 59(2): 125-148.

[7]Yager R R. On ordered weighted averaging aggregation operators in multicriteria decision making[J]. IEEE Transactions on Systems, Man and Cybernetics, 1988, 18(1): 183-190.

[8]徐泽水. 拓展的C-OWA算子及其在不确定多属性决策中的应用[J]. 系统工程理论与实践, 2005, 7(11): 7-13.

[9]王煜, 徐泽水. OWA算子赋权新方法[J]. 数学的实践与认识, 2008, 38(3): 52-61.

[10]赵金先, 李龙, 刘敏. 基于OWA算子赋权的地铁工程项目管理绩效灰色评价[J]. 建筑经济, 2014, 35(9): 125-129.

[11]邓聚龙. 灰色控制系统[M]. 武汉: 华中工学院出版社, 1985.

[12]刘思峰, 谢乃明. 基于改进三角白化权函数的灰评估新方法[J]. 系统工程学报, 2011, 26(2): 244-250.

[13]李龙. 钻爆法地铁隧道工程风险集成管理研究[D].青岛: 青岛理工大学, 2014.

Grey Clustering Evaluation of Reinforced Concrete Construction Quality

Based on PCA and C-OWA Operator

CHENWei-gong,ZHANGSheng-xi,WANGHui-hui

(School of Management, Qingdao Technological University, Qingdao 266520, China)

Abstract:Reinforced concrete structure with its integrity, stability, durability, has gradually become a common form of structure in a construction. The construction quality of reinforced concrete is the main factor that affects the durability and safety of buildings, and its quality is directly related to the overall quality of construction projects. Because there are many factors affecting the quality of reinforced concrete construction with strong fuzzy, grey and uncertainty characteristics, elements set that affects the quality of the reinforced concrete in the evaluation set is proposed based on the principle of scientific, real, and can be operated, and the set of 26 elements in PCA dimensionality reduction, the obtained 10 main components of the combination of engineering practice experience are summarized and analyzed to construct quality evaluation on the index system of reinforced concrete construction based on the principal component analysis method. Using the C-OWA operator to evaluate the objective weight, and combining the grey clustering evaluation model to evaluate the model, the objective quality level of fuzzy and gray is obtained. Eventually, the validity of the method is verified by empirical research.

Key words：reinforced concrete; construction quality; principal component analysis; C-OWA operator; gray clustering evaluation

中图分类号：TU712+.3

文献标识码：A

文章编号：2095-0985(2016)01-0001-06

基金项目：国家自然科学基金(71471094)

作者简介：陈为公(1971-)，男，辽宁沈阳人，教授，硕士，研究方向为建设项目管理、地质环境评价(Email: ch.ylh@163.com)

收稿日期：2015-09-12修回日期： 2015-10-27