试论高中数学“一题多解”的学习心得

⌾ 柳世杰

试论高中数学“一题多解”的学习心得

⌾ 柳世杰

问题是学习数学的核心部分，学好数学的最终目的就是灵活的使用数学知识去解决数学问题。但是，在不断的解题过程中我们发现，不管我们已经解决了多少问题，依然有很多问题等着我们。由此可见，掌握数学不在于你解决了多少问题，而在于你是否掌握了正确的解题思路。很多高中生在解决数学问题的时候会发现，同一道数学题能够用多种方式进行解答，并且都能够得到准确的答案。因此，高中生在学习数学的时候，应该从多个角度进行思考，积极的尝试不同的解题方式，对于拓宽高中生的解题思路有很大的帮助。

高中数学；“一题多解”；学习心得

前言：解决数学问题一直是高中数学教育的重点，也是培养高中生数学能力非常重要的一个环节。数学学习最重要的是练习，在解题的过程中能够了解自己在某一知识点上的不足，起到查缺补漏的作用。现阶段高中生在解决数学习题的时候一般都使用“题海战术”的方式，机械性的重复进行解题，无法充分理解题干中含义，对于数学知识的利用率非常低，对数学问题的思考模式还比较单一，没有从多个角度进行分析。

一、高中生解决数学习题时存在的问题

1.数学基础知识点掌握不扎实 解决数学问题能够对数学知识点进行巩固，帮助高中生发现自身存在的问题，并且针对问题进行查缺补漏，更好的将各种数学知识灵活的运用在数学习题中。也就是说，要想彻底的解决数学问题，就必须要对数学基础知识点进行熟练的掌握。在数学学习的过程中，需要不断的接收新知识，而在积累新知识的同时，难免会遗忘旧知识，造成了高中生对数学基础知识点掌握不扎实，无法充分发挥出数学知识在解题中的重要作用。另外，数学基础知识点的掌握不扎实还会影响到解题速度和效果，无法确保解决问题的准确性，给高中学习数学时增加了很大的难度[1]。

2.无法灵活的运用各种数学知识 数学相关知识点之间都存在着一种特殊的联系，可能相同的知识点在不同类型的数学习题中都发挥着关键的作用。像是在解决代数问题和几何运算的时候，经常会遇到各种各样的数学知识点，只有能够对这些数学知识点进行数量的掌握，并且灵活的使用在解决数学问题的过程中，才能够有效提升高中生学习数学的质量。高中数学知识点之间具有衔接性差、分离性大的基本特征，教师在授课的过程中都采用单独学习的教学模式，没有将各种数学知识点进行统一的整合，学生无法了解到各个数学知识点之间的关联。很多时候，学生掌握了丰富的数学知识点，并且对知识点的记忆也非常的牢固，但是在解决问题的时候，却不知道应该使用哪一种知识点来解决问题，给高中生数学的学习造成了很大的制约[2]。

二、高中数学“一题多解”的例题分析

以高中数学中的圆锥曲线方程类问题为例，在解决这一类问题的时候，就可以利用多种解题方式。

例1共有两种解决方式，一种是常用的代数法，另一种是数形结合法。下面笔者将针对这两种解题方法进行比较分析。

解法1：

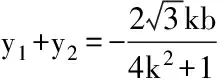
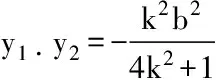
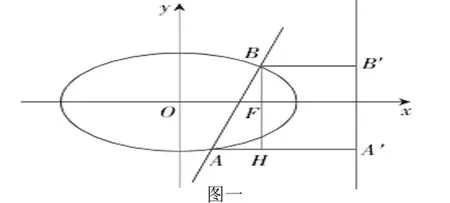
使用代数法来解决高中数学圆锥曲线方程类问题的过程非常复杂，最后一步的消元过程还伴随着一定量的计算，如果是一道选择题就会浪费高中生很多不必要的时间。用于平时练习运算量、运算能力还可以，如果在考试中也使用代数法去解决高中数学圆锥曲线方程类问题，就会影响到学生的解题速度。所以，我们要找到其他方式去解决高中高中数学圆锥曲线方程类问题，灵活运用圆锥曲线的定义，使用数形结合的方法化繁为简，大大的提升了高中生的解题速度。我们要灵活的运用圆锥曲线的相关知识，如图一所示，过点A、B做一条垂线，构造直角梯形ABB/A/、直角三角形ABH，将题中的数量关系转化到直角梯形上面，在分析、解题方面都更加的清晰、简单[3]。

解法2：

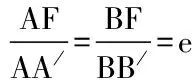
解法2就要比解法1简单的多，利用圆锥曲线的定义把椭圆上A点和B点到焦点的距离转化成相应准线的距离，利用图形的几何特征和数量关系进行分析，更好的解决了圆锥曲线方程类问题，最重要的是在实际解题过程中，不会涉及到很多的计算量，大大的提升了高中生的解题速度，降低了我们出现解题错误的概率[4]。

三、高中数学“一题多解”的应用

1.举一反三 高中数学中的“一题多解”能够起到举一反三的作用，帮助学生熟练的掌握相关的数学知识点和定理，了解不同类型数学习题中的解题规律，并且在笔记、错题本上记录学习心得，通过这种方式来对数学解题过程中进行经验总结。“一题多解”的方式就是告诉高中生在解题的过程中，应该从多个角度去进行思考，打破传统的单一思考模式，运用自己所学的数学基础知识灵活的应用于数学习题当中，找到最佳的解决方式来解决实际问题，为学生的解题过程节省更多的实践，全面提升了高中生的解题效率，对于提高解题结果的准确性也有一定的帮助[5]。

2.系统化解题 “一题多解”的解题模式能够锻炼高中生的思维分析能力，对于拓宽高中生知识视野的深度和广度有着积极的意义，帮助高中生更加系统化的进行解题。在“一题多解”的实践环节中，我们发现其最终目的并不是解决问题，而是从众多的解题方法中找到最简单的方法。从某种角度来看，“一题多解”也是总结数学问题最佳解题途径的有效方式[6]。

结论：综上分析可知，“一题多解”的解题模式打破了高中生惯用的思维模式，是对高中生解题方式的创新与升级。平常的练习中通过“一题多解”的方式可以提升高中生的发散性思维，对于拓宽高中生知识视野的深度与广度有着积极的意义。学习在利用“一题多解”方式进行数学学习的过程中，能够做到融会贯通、举一反三，在遇到不同类型习题的时候，也能够熟练的利用自己掌握的数学基础知识构建知识网络，找到最佳的解决方案，从而提高解题效率。

[1]宁继淦.高中数学“一题多解”的学习心得[J].新课程

[2]伍俊溢,廖俊淇.高中数学“一题多解”的学习心得[J].考试周刊

[3]邓海棠.沪澳高中毕业生数学开放题解题能力比较.华东师范大学

[4]张嘉玲.上海高中数学试卷评讲课的有效性研究.上海师范大学

[5]李健.“一题多解”与“多题一解”在高中数学教学中的价值研究与实践[D].苏州大学,2012.

[6]刘金利.提高高中数学学困生解题能力的策略研究——以贵州师大附中高二年级为例[D].贵州师范大学,2015.

湖南省长沙市明德中学K358班 410000)