高中物理中的“微元法”

⌾ 聂宇旋

高中物理中的“微元法”

⌾ 聂宇旋

升入高三研习近年高考物理试题，发现涉及微元法的题目近年多有出现，而自己和周围的同学对此类题目也都比较陌生，按照老师回归课本的要求，发现中学课本中对微元法多次涉及。

一、课本中的微元法

1、瞬时速度的定义：必修1课本中对瞬时速度的定义是 ,当Δt极小时，就认为是物体的瞬时速度。

2、匀变速直线运动的位移：必修1课本采用先微分再求和的方法从匀速直线运动位移得到匀变速直线运动位移关系。将物体运动过程分为很多小段，每一小段的位移Δx=ΔV*Δt，所有小段位移之和就是整个过程的总位移，用v-t图表示出来就是与横轴围成的“面积”。

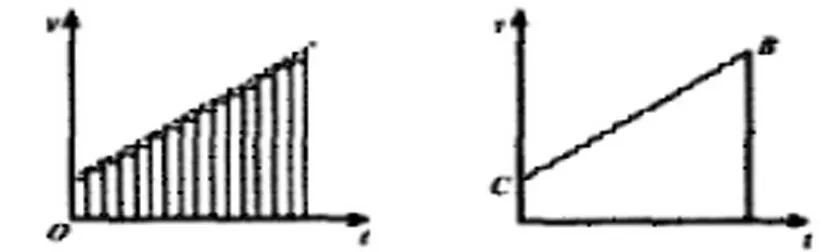
3、圆周运动向心加速度公式：在必修2课本中，提供了向心加速度表达式的推导过程，“当中ΔV很小的时候就表示加速度”。

……

二、微元法总结：

将物理量分割成无数个小块，每一块称为一个微元，再对这些微元求和(积分)就得到了物理量的变化ΣΔt=t，ΣΔx=x，ΣΔv=v，微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

三、微元法应用举例：

例题1.(2013全国课标卷I)如图，两条平行导轨所在平面与水平地面的夹角为θ，间距为L。导轨上端接有一平行板电容器，电容为C。导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面。在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑，求：

⑴电容器极板上积累的电荷量与金属棒速度大小的关系；

⑵金属棒的速度大小随时间变化的关系。

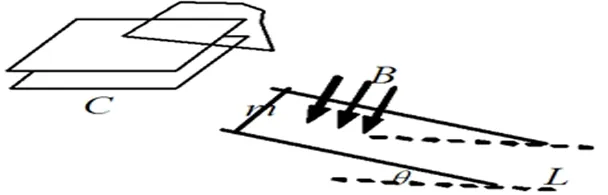
【解析】(1)设金属棒下滑的速度大小为v，则感应电动势为

E=BLv①

平行板电容器两极板之间的电势差为

U=E②

设此时电容器极板上积累的电荷量为Q，按定义有

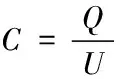
联立①②③式得

Q=CBLv④

(2)设金属棒的速度大小为v时经历的时间为t，通过金属棒的电流为i，金属棒受到的磁场的作用力方向沿导轨向上，大小为

f1=BLi⑤

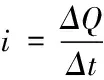
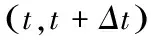
ΔQ=CBLΔv⑦

式中，Δv为金属棒的速度变化量，按定义有

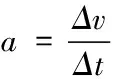
金属棒所受的摩擦力方向斜向上，大小为

f2=μN⑨

式中，N是金属棒对于导轨的正压力的大小，有

N=mgcosθ⑩

金属棒在时刻t的加速度方向沿斜面向下，设其大小为a，根据牛顿第二定律有

mgsinθ-f1-f2=ma⑾

联立⑤至⑾式得

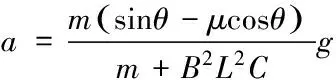
由⑿式及题设可知，金属棒做初速度为零的匀加速运动。T时刻金属棒的速度大小为

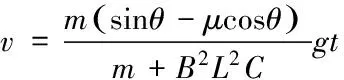
例2.(1999上海)如图所示，长电阻r=0.3Ω、m=0.1kg的金属棒CD垂直跨搁在位于水平面上的两条平行光滑金属导轨上，两导轨间距也是L，棒与导轨间接触良好，导轨电阻不计，导轨左端接有R=0.5Ω的电阻，量程为0～3.0A的电流表串接在一条导轨上，量程为0～1.0V的电压表接在电阻R的两端，垂直导轨平面的匀强磁场向下穿过平面。现以向右恒定外力F使金属棒右移。当金属棒以v=2m/s的速度在导轨平面上匀速滑动时，观察到电路中的一个电表正好满偏，而另一个电表未满偏。问：⑴此满偏的电表是哪个表？说明理由。⑵拉动金属棒的外力F多大？(3)此时撤去外力F，金属棒将逐渐慢下来，最终停止在导轨上。求从撤去外力到金属棒停止运动的过程中通过电阻R的电量。

解析(1)U=I(R+r)，当U=1V时，I=1.25A，所以电压表先满偏。

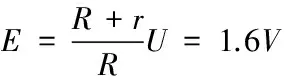
总结：高考物理重视重点知识和能力考查，本文所述微元法和近似法等都是课本中重要的思想方法，高三冲刺阶段应该加以重视。

河北省唐山市丰南区第一中学 063300)