浅谈数学模型在物理问题中的应用

⌾ 于小帆

浅谈数学模型在物理问题中的应用

⌾ 于小帆

数学是解决物理问题的重要工具，应用数学知识解决物理问题，是中学物理《考试大纲》要求学生必须具备的五种能力之一，借助数学知识和数学方法可以优化、拓宽解决物理问题的思路，达到事半功倍的效果。对此，笔者试着借助实例简单谈一谈数学模型在物理问题中的具体应用。

应用 ；思维 ；元法； 模型

一、微元法

微元法指的是将研究对象或过程分隔成无限多个无限小的部分(即微元)加以研究，再将结果推广到整体的思维方法。这种方法在人教版中最为突出，例如瞬时速度、瞬时加速度、感应电动势等等，都是用这种方法定义的。

微元法解题的思维过如下：

1.取元。选取的微元可以是一小段线段、圆弧或一小块面积，也可以是一个小体积、小质量或一小段时间等，但必须具有整体对象的基本特征。

2.微元模型化。(可视为质点、恒力、点电荷、匀速直线运动等)，并运用相关知识建立这个微元与所求量之间的关联。

3.求和。将这个微元的解答结果推广到其他微元，并利用各微元间的对称关系、矢量关系、近似极限关系等，对各微元的求解结果进行叠加，以求得整体量的合理解答。

例1[2014·江苏卷·4题] 如1图所示，一圆环上均匀分布着正电荷，x轴垂直于环面且过圆心O.下列关于x轴上的电场强度和电势的说法中正确的是( )

A．O点的电场强度为零，电势最低

B．O点的电场强度为零，电势最高

C．从O点沿x轴正方向，电场强度减小，电势升高

D．从O点沿x轴正方向，电场强度增大，电势降低

[解析]本题将带电圆环分割成无限个无限小的圆弧，将每一小段圆弧视为点电荷，则任意两个关于圆心对称的点电荷在圆心O处产生的电场的合场强为零，将这一结果推广到其他微元，根据圆的对称性可知，整个圆环在圆心O处产生电场的合场强为零。同理可知，从O 点沿x 轴正方向，电场强度先变大后变小，方向沿x轴正方向；从O 点沿x 轴负方向，电场强度先变大后变小，方向沿x轴负方向。综上所述，只有选项B正确。

二、图像法

图像法是历年高考热点，学生通过对物理问题的分析，建立物理量间的联系从而作出图像，利用图像的斜率、截距、交点及面积等解题，使问题形象化、简单化。

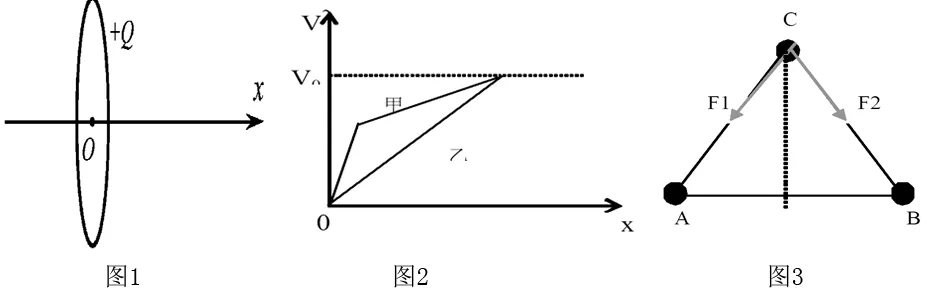
例2.甲、乙同时从A处由静止出发，沿直线AB运动，甲先以加速度a1做匀加速运动，经一段时间后，改以加速度a2做匀加速运动，到达B点的速度为v0，乙一直以加速度a做匀加速运动，到达B的速度也为v0.已知a1>a2，则( )

A.a2=a B.a2>aC.经过AB间任一点时甲的速度一定大于乙的速度

D.经过AB间某一点时，甲的速度可能小于乙的速度

[解析]由匀变速直线运动的公式v2=2ax知，v2-x图线是一过原点的直线，其斜率的数值为加速度大小的两倍。做出v2-x图像如2图所示，由图可知，a2

三、均值不等式的应用

(1)如果a、b为正数，那么有，当且仅当a=b时，上式取“=”号。

若两个正数的积一定，则两数相等时和最小；

若两个正数的和一定，则两数相等时积最大。

(2)如果a，b，c为正数，则有，当且仅当a=b=c时，上式取“=”号。

若三个正数的积一定，则三数相等时和最小；

若三个正数的和一定，则三数相等时积最大。

例3.如3图两个电量均为+Q的小球A、B固定，将另一个电量为-q的小球C由A、B两球连线的中点沿中垂线移至无穷远处，则此过程中小球C受A、B两球静电力的合力大小如何变化？

[解析]设AB=2l，∠CAB=∠ɑ，AC=r

令y=cos2αsinα

物理离不开数学，数学作为工具学科，其模型、方法贯穿于整个高中物理的学习过程,因此学生在物理学习中要重视数学模型和数学方法的应用。

辽宁省葫芦岛市绥中县第一高级中学 125200)