基于主动特征选择的非合作航天器鲁棒视觉导航方法研究

宁明峰,张世杰, 张翰墨

(1.哈尔滨工业大学 卫星技术研究所,黑龙江 哈尔滨 150080; 2.上海航天控制技术研究所，上海 201109)

基于主动特征选择的非合作航天器鲁棒视觉导航方法研究

宁明峰1,张世杰1, 张翰墨2

(1.哈尔滨工业大学 卫星技术研究所,黑龙江 哈尔滨 150080; 2.上海航天控制技术研究所，上海 201109)

面向非合作目标航天器近距离操作任务，针对采用自然特征的单目视觉相对位姿参数确定过程中特征提取与匹配导致的粗大误差增加导致结果不准确甚至错误，以及特征数量多增大计算量等问题，提出一种融合随机采样一致性(RANSAC)算法和主动特征选择的鲁棒视觉导航方法。用RANSAC算法剔除有粗大误差的特征点，给出了基于RANSAC的特征点选择步骤；根据不同特征点组合所计算的克拉美罗(CRLB)不同，用参数化CRLB下限选择对位姿确定精度有显著影响的点以减少参与计算的特征数量，给出了基于CRLB的特征点选择流程。仿真结果表明：综合RANSAC和CRLB的特征点选择方法可显著减少特征点数量，提高了位姿解算精度。

非合作目标； 视觉导航； 特征点选择； RANSAC； CRLB； 特征点数； 鲁棒性； 位姿精度

0 引言

目前，航天器在轨维修等非合作航天器接近任务是航天器相对导航的主要应用之一。与合作航天器目标不同，非合作目标航天器未安装目标标识器，追踪航天器不能直接获得固定的标识器特征信息。这增大了目标航天器特征点提取与匹配的难度，降低了位姿解算的精度。因此，选择非合作目标表面特征点以提高解算精度，是目前亟需解决的问题之一。航天器有明显的边缘点和角点，可作为目标特征点，结合航天器自身结构信息，将航天器模型简化为特征点模型，进而可基于这些特征点解算相对状态信息。用这种方法，可充分利用航天器表面特征，在不安装目标标识器条件下能计算相对状态，适于非合作目标的相对状态测量[1-2]。文献[3]针对模型尺寸已知的非合作目标，在目标三维特征点和图像二维特征点坐标已知但匹配关系未知的条件下，对基于SoftPOSIT算法的非合作目标航天器间相对位姿估计方法进行了研究，所得结果精度较高。但因空间光照及航天器表面特征不明显，导致特征点提取难度大且易造成个别特征点的提取和匹配误差大[4]。若将这些特征直接用于相对状态解算，则会导致计算结果偏差过大甚至出现计算结果错误。另外，考虑不同特征点对解算精度的影响各异，需用一种新方法从提取的特征点中选取一定数量的特征点，以提高目标航天器与追踪航天器的相对状态信息解算精度。为此，本文对基于主动特征选择的非合作航天器鲁棒视觉导航方法进行了研究，采用RANSAC算法剔除特征点中有粗大误差的点，利用参数化CRLB的特征有效模型，从RANSAC计算的内点中选取使CRLB最小的特征点集合用于求解相对状态参数。由于RANSAC消除了误差大的点，用CRLB模型从已有点中选取最优解算的最小集合，提出的鲁棒性特征点选择算法有较高的精度。

1 坐标系定义及相机模型

图像坐标系：原点位于图像平面的左上角；μ，ν分别为像素的水平与垂直坐标。图像的像素坐标为(μ，ν)。

相机坐标系：以投影中心为坐标原点；Oczc轴与光轴重合；Ocxc、Ocyc轴分别与图像像素坐标系中的μ、ν轴平行且方向一致，Ocxc、Ocyc、Oczc轴构成右手坐标系。

目标航天器体坐标系OI-XIYIZI：为固连坐标系，原点为目标航天器质心；三轴分别沿三个惯性主轴，构成右手坐标系。

各坐标系如图1所示。

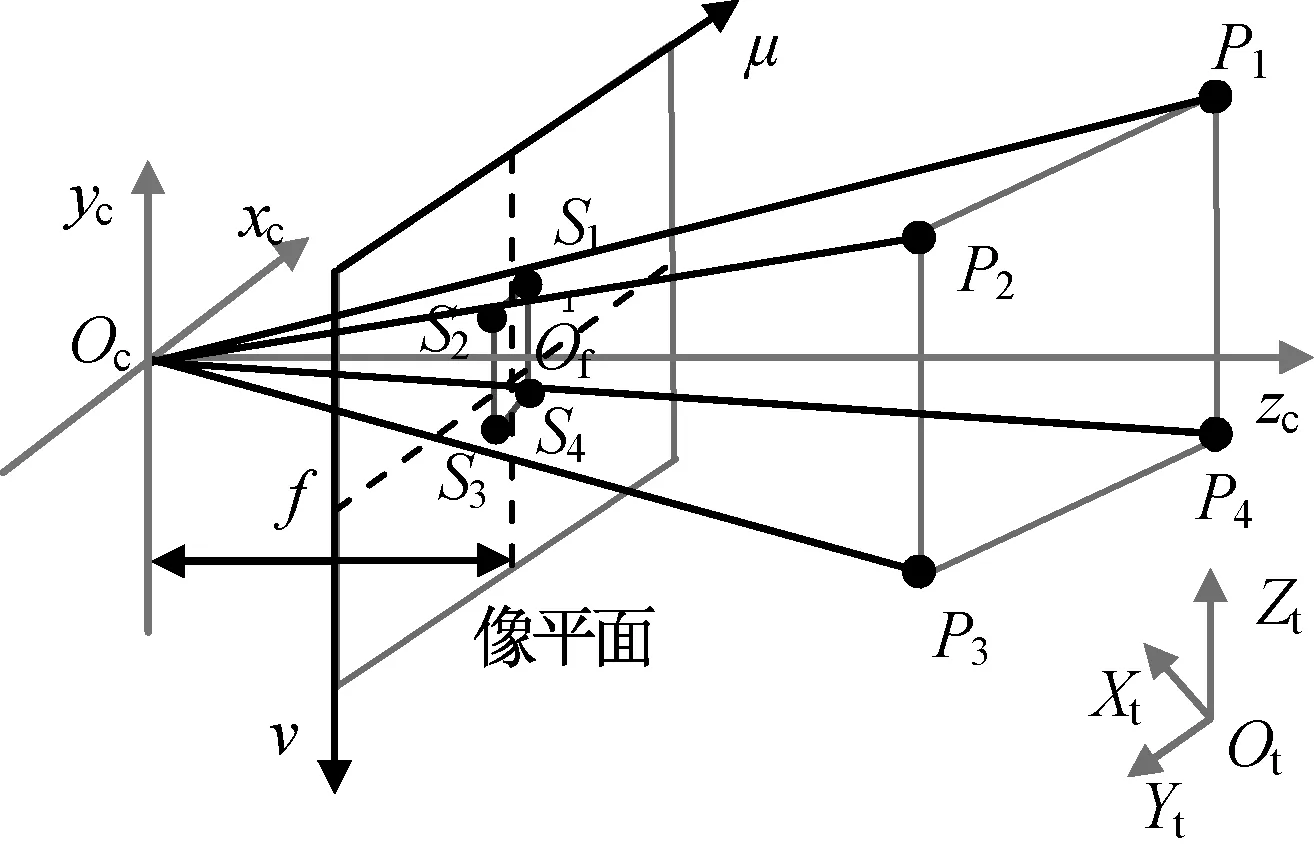
图1 相机模型及坐标系定义Fig.1 Camera model and coordinate system definitions

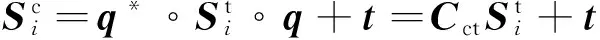
(1)

式中：q为姿态四元数；符号“*”表示共轭；Cct为目标航天器坐标系至追踪航天器体坐标系的转换矩阵；t为目标航天器坐标系质心在相机坐标中的坐标[5-6]。另在图像坐标系中，有

(2)

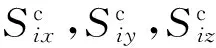
2 鲁棒性特征点选择方法

2.1 总体方案

在视觉导航过程中，获取的目标图像包含各种特征，可能有背景特征、航天器尖锐的角点特征、太阳帆板等有明显几何形状的特征。航天器视觉导航特征选择的基本任务是从航天器众多的特征点中剔除图像处理产生的粗大误差及虚假无效特征，从而获得最优表决集。在此基础上，用CRLB减少冗余特征并选择空间构型优异的特征，减少计算量并提高视觉导航算法的鲁棒性。总体方案如图2所示。

图2 鲁棒性特征点选择方法总体方案Fig.2 Robust feature point selection method overall scheme

假设目标航天器模型已知，追踪航天器中有目标航天器的表面特征信息。当获取目标航天器图像后，处理得到目标航天器表面特征特征点信息。获得图像后，将其与追踪航天器中保存的图像或上一幅图进行特征对比并匹配，获取其对应特征点先验信息。这些特征点作为待选特征点，经由RANSAC，CRLB选点后，获得所需的特征点，将最后得到的特征点用于相对位姿计算。

2.2 RANSAC算法

传统的视觉导航相对状态估计算法，如最小二乘法等，利用提供的所有测量值最优化拟合目标函数。这些算法未采取任何措施判断和剔除粗大误差，均建立在平滑假设基础上，因此无论测量集的大小，总存在足够多的数据平滑任何粗大误差[7-8]。但实际的相对状态解算过程并不能保证平滑假设成立，即测量结果中包含不可平滑的粗大误差。为处理这种情况，常先用所有数据计算模型参数，再确定偏离该模型最远的数据，假设其为粗大误差予以剔除，重复上述过程直至最大数据偏差小于某预先设定的阈值或没有足够的数据进行上述过程。当一组有效数据中混入一个粗大误差时上述探索性方法易失效。因此，平均法不是处理含粗大误差数据的合适算法，使用特征点前必须降低这些粗大误差的影响。

RANSAC算法可有效解决此问题。其要点是首先根据具体问题设计某种目标函数，然后通过反复提取最小点集估计该函数中的初值，利用这些初始参数值根据一定的判断准则将所有的数据分为“内点”(满足估计参数的点)和“外点”(不满足估计的参数点)，由所有内点组成的点集称为最小点集的表决集，利用满足一定条件的有效表决集内的所有“内点”重新计算和估计函数的参数。本文基于RANSAC的特征点选择方法过程如下。

步骤1：从所有特征点中随机选择6个，建立估计模型，恢复相对状态信息。

步骤2：用步骤1建立的模型测试其它特征点数据，若某个特征点适于估计模型，则将其作为“内点”；否则，认为该点为“外点”。

步骤3：若有足够多的“内点”满足某一估计模型，则认为该模型足够合理，满足该模型的所有“内点”即为RANSAC所筛选的特征点，结束筛选。

步骤4：若测试完所有特征点仍没有足够多的“内点”满足某一模型，则认为该模型不合理，重新从步骤1开始。

步骤5：若以上过程被执行预先设定次数后，每次都因无足够多“内点”形成模型被舍弃，则使用RANSAC选择特征点失败。这表明此图像不适于解算相对状态信息，舍弃该图像。

RANSAC是一种简单但具有高鲁棒性的算法，用其可基本剔除粗大误差的特征点，满足平滑假设。

2.3 基于CRLB的特征点自适应选择方法

CRLB表示了一个确定参数估计的协方差的下界，是最简单的形式——边界状态。如一个无偏估计达到此下界，可以称为全效率。此结果在所有无偏估计方法中达到了一个最小的均方误差，因此也可称作是最小协方差(MVU)估计[9-11]。

CRLB可表示为

(3)

(4)

式中：p(x;θ)为待估计变量θ与观测值x的极大似然函数。

相对位姿视觉测量的CRLB模型建立如下。假设特征点x、y轴均受到高斯白噪声(0,σ2)影响，特征点数为N，估计所求变量

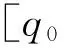
的最低方差，其极大似然函数

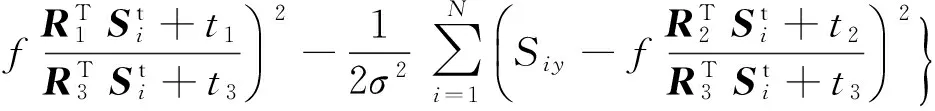
(5)

式中：q0，q1，q2，q3为q的四个分量。

式(5)取对数，有

(6)

(7)

式中：d=1，2，3；i=1，2，3,…，N。可得对各估计量求二阶偏导表达式如下。

a)期望Et1t1

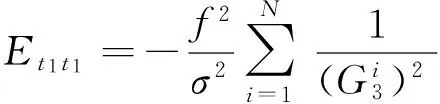
(8)

b)dt1t2的期望Et1t2

Et1t2=dt1t2=0.

(9)

c)dt1t3的期望Et1t3

(10)

d)dt1q的期望Et1q

(11)

e)dt2t2的期望Et2t2

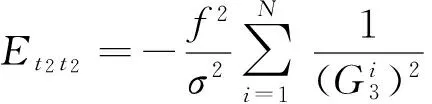
(12)

f)dt2t3的期望Et2t3

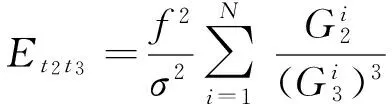
(13)

g)dt2q的期望Et2q

(14)

h)dt3t3的期望Et3t3

(15)

i)dt3q的期望Et3q

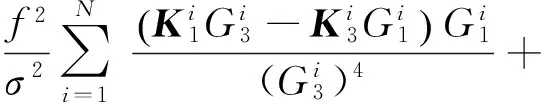
(16)

j)dqq的期望Eqq

Eqq=

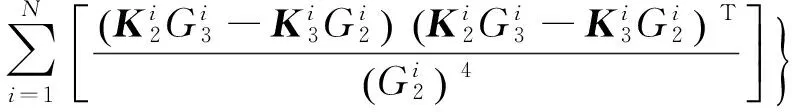
(17)

可得基于特征点的位姿参数估计的方差满足

(18)

式中：Mθ为位姿参数估计的参数；

(19)

2.4 基于CRLB特征点选择

RANSAC剔除了提取匹配特征点中具有粗大误差的特征点，由于各“内点”误差及位置不同，其对解算结果的影响亦不相同，必然会导致不同“内点”解算的相对状态精度影响各异。

在所有“内点”中，如采用误差小且具有较好相对位置的部分“内点”组合解算相对状态，其解算精度必高于将所有“内点”作为特征点解算。为能从所有“内点”中搜索满足高精度要求的“内点”组合，需要一个精度评价标准以评判所搜索的“内点”组合能有效提高精度。

相对位姿视觉测量的CRLB表示的含义是，对不同给定特征点其所解算的相对状态方差最小不同。因此，可将该模型作为这个精度评价标准，当选择“内点”组合后，将该组合解算的CRLB下限与其它组合解算的CRLB下限进行比较，以选定能解算出更高精度的特征点组合。

因相对位姿的CRLB模型对姿态四元数与位移进行参数化，计算所得的CRLB下限由相应的7个CRLB构成。为能对特征点进行比较，本文将各变量的CRLB计算结果加权相加。借鉴RANSAC算法，CRLB下限特征点选择开始时依然选择6个特征点计算其CRLB下限的加权值，并将其与所有RANSAC选择的“内点”CRLB加权值比较，若所选的6个特征点CRLB加权值大于所有“内点”CRLB加权值，则表明，所选择的点组合不合理，重新选择6个计算；若每次所选择初始特征点的CRLB加权值均大于所有“内点”组合的CRLB加权值，且选择次数超过阈值，则认为经过RANSAC所选的“内点”较合理，之后用所有“内点”进行相对状态计算。

若选择的初始特征点CRLB加权值小于所有“内点”CRLB下限加权值，则将剩余“内点”逐个加入特征点组合并将新组合与之前组合CRLB加权值比较，若使CRLB加权值变小，则保留该点在特征点组合直至测试完所有“内点”。最终的特征点组合即为选择的特征点，用这组特征点组合计算相对状态信息。

本文基于CRLB下限的特征点选择借鉴RANSAC剔除流程如图3所示。

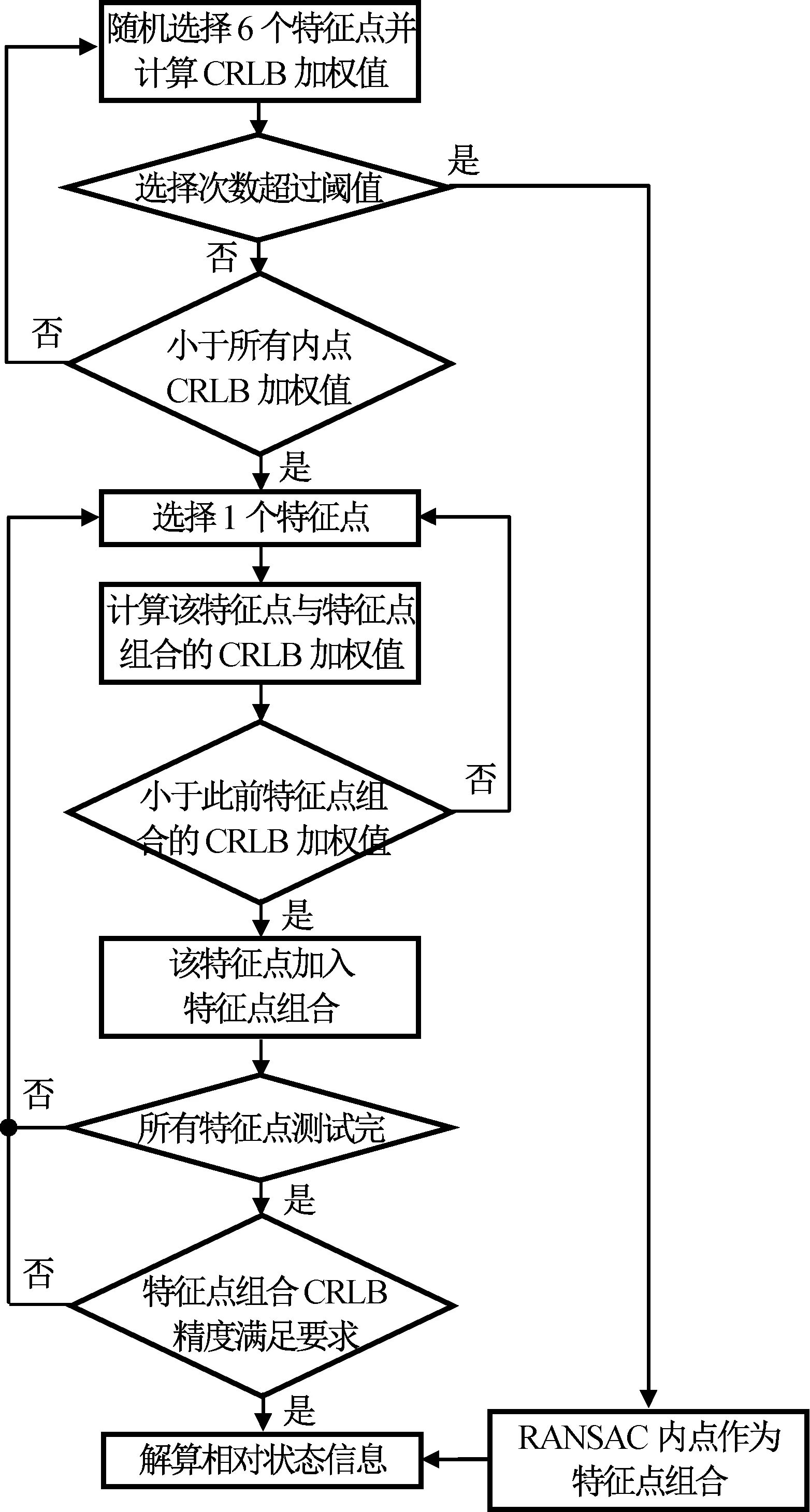
图3 基于CRLB特征点选择流程Fig.3 CRLB-based feature point selection process

3 仿真验证

非合作目标航天器表面无特定标识，只能利用其表面特征。在空间环境中，特征点提取与匹配的难度大于合作目标特征点，同时其误差亦较大。以在轨服务非合作目标相对位姿测量为背景，用仿真验证本文的鲁棒特征点选择方法。

假设目标航天器表面特征已知，实际相对位姿参数为相对位置矢量[1 1.2 10] m；相对姿态角[15° 20° 10°]；相机焦距0.01 m。仿真产生的数据在22 m2平面上，平面在目标航天器1 m处随机生成。每次仿真初始特征点介于160～180个不等，90%特征点误差随机采用方差0.02，0.1 mm2中的一种；10%特征点的方差3 mm2。

连续仿真300次，所得单独RANSAC计算与采用CRLB及RANSAC组合后的位置与姿态角误差分别如图4、5所示。

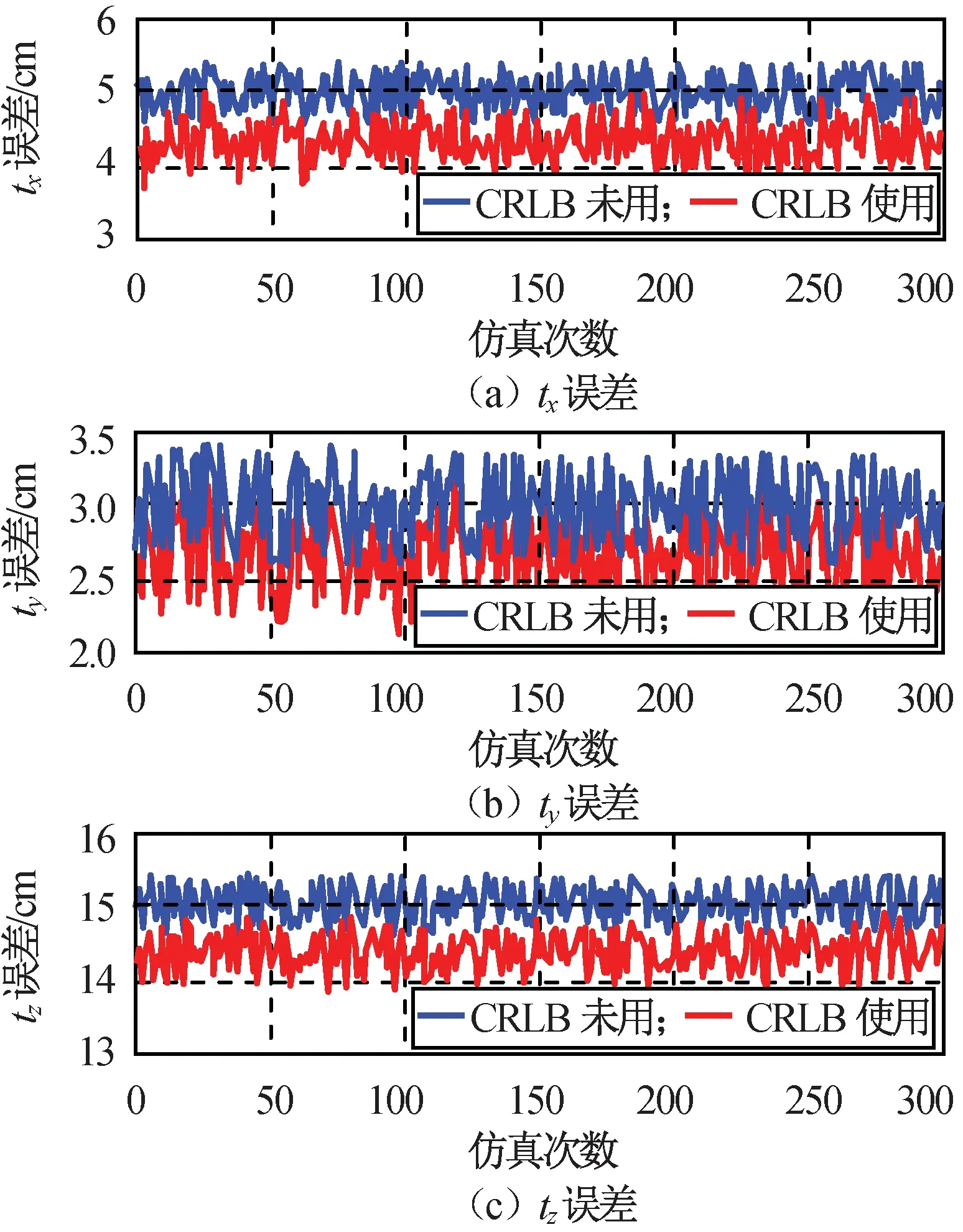
图4 CRLB选择后位置误差Fig.4 Position error comparison

图5 CRLB选择后姿态误差Fig.5 Attitude error comparison

由图4、5可知：经CRLB选点后的特征点解算的相对位置状态信息精度高于只采用RANSAC方法，其解算精度有明显提高。

为验证使用该算法后特征点数变化，连续仿真80次，所得特征点数分布结果如图6所示。

图6 仿真80次特征点选择数分布Fig.6 Number of feature points distribution aftersimulation 80 times

由图6可知：经CRLB筛选后的特征点数仅为只用RANSAC方法选点数的约三分之二，这将显著提高后续解算速度；仿真时出现采用CRLB选点前后数一样多，表明此次仿真没有符合CRLB选点的特征点组合，直接采用RANSAC选择的特征点解算相对位姿。

4 结束语

本文针对在轨维修等非合作目标航天器空间视觉导航过程中，特征点提取与匹配过程中出现的粗大误差，影响解算精度的问题，在RANSAC算法的基础上，提出了一种有高鲁棒性的RANSAC与CRLB结合的选点方法。该法显著减少了有效特征点数量，同时提高了位姿解算精度。对本文的算法进行了数值仿真，验证了其在对特征点数量减少与解算精度提高的有效性。

[1] MATTHIES L, BROCKERS R, KUWATAY, et al. Stereo vision-based obstacle avoidance for micro air vehicles using disparity space[C]∥ 2014 IEEE

International Conference on Robotics and Automation (ICRA). IEEE, 2014: 3242-3249.

[2] WEEDEN B C, CHOW T, LUKASZCZYK A, et al. International perspectives on on-orbit satellite servicing and active debris removal and recommendations for a sustainable path forward[C]// 64thInternational Astronautical Congress. Beijing: [s. n.], 2013: IAC-13, E34, 7, X16786.

[3] 张鑫, 张雅声, 程文华, 等. 基于SoftPOSIT算法的单目视觉非合作目标相对位姿估计[J]. 上海航天, 2016, 33(3): 124-129.

[4] WU Y H, GAO Y, LIN J W, et al. Low-cost, high-performance monocular vision system for air bearing table attitude determination[J]. Journal of Spacecraft and Rockets, 2013, 51(1): 66-75.

[5] TWEDDLE B E, SAENZ-OTERO A. Relative computer vision-based navigation for small inspection spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(5): 969-978.

[6] TWEDDLE B E, SAENZ-OTERO A. Relative computer vision-based navigation for small inspection spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(5): 969-978.

[7] ZHANG K, ZHANG L, YANG M H, et al. Robust object tracking via active feature selection[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2013, 23(11): 1957-1967.

[8] 张世杰, 谭校纳, 曹喜滨. 非合作航天器相对位姿的鲁棒视觉确定方法[J]. 哈尔滨工业大学学报, 2009, 41(7): 6-10.

[9] ZUO L, NIU R, VARSHNEY P K. Posterior CRLB based sensor selection for target tracking in sensor networks[C]// 2007 IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP'07. [S. l.]: IEEE, 2007, 2: Ⅱ-1041-Ⅱ-1044.

[10] GRISHINV A. A Cramer-Rao bound for the measurement accuracy of motion parameters and the accuracy of reconstruction of a surface profile observed by a binocular vision system[J]. Pattern Recognition and Image Analysis, 2008, 18(3): 507-513.

[11] LENG M, TAY W P, SEE C M S, et al. Modified CRLB for cooperative geolocation of two devices using signals of opportunity[J]. IEEE Transactions on Wireless Communications, 2014, 13(7): 3636-3649.

Robust Method Study of Active Feature Selection for Non-Cooperative Spacecraft Vision-Based Navigation

NING Ming-feng1, ZHANG Shi-jie1， ZHANG Han-mo2

(1. Research center of Satellite Technology, Harbin Institute of Technology, Harbin 150080, Heilongjiang, China; 2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

To solve the problem that the error of feature points extracting or matching and the number of feature points would lead to inaccurate results or the wrong results and huge amount of calculation on the relative position and attitude parameter determination during non-cooperative target spacecraft proximity operations, a robust method for vision navigation fusing the random sample consensus (RANSAC) algorithm and an active feature selection method was put forward in this paper. First the gross error was eliminated by RANSAC algorithm. The selection steps for feature points were given based on RANSAC algorithm. Then the different points, which had significant impact on determining precision based on Cramér-Rao lower bound (CRLB), were selected to reduce the number of feature involved in the calculation according to the different CRLB calculated from various feature points sets. The features selection flowchart was given based on CRLB. The simulation results showed the selected points by combining of RANSAC and CRLB could be reduced and the precision of position and attitude had been improved.

Non-cooperative spacecraft; Visual navigation; Feature point selection; Random sample consensus (RANSAC); Cramér-Rao lower bound (CRLB); Feature point number; Robust; Precision of position and attitude

1006-1630(2016)06-0136-06

2016-07-05；

2016-11-10

上海航天科技创新基金资助(SAST201444)

宁明峰(1989-)，男，博士生， 主要研究方向为航天器视觉导航与控制。

V448.2

A

10.19328/j.cnki.1006-1630.2016.06.020