一种遥感卫星宽幅无盲区拼接成像路径自主规划方法研究

唐文国,张国云,朱庆华,许贤峰

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109;3.西安卫星测控中心，陕西 西安 710043)

一种遥感卫星宽幅无盲区拼接成像路径自主规划方法研究

唐文国1、2,张国云3,朱庆华1、2,许贤峰1、2

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109;3.西安卫星测控中心，陕西 西安 710043)

为解决低幅宽卫星载荷因幅宽小而导致成像覆盖物面窄、效率低、使用复杂的缺陷，提出了一种多条带拼接成像路径自主规划方法。先完成单次侧摆成像规划：通过卫星、目标相对位置关系判断成像时机，规划包括姿态机动开始时刻、成像开始时刻、成像结束时刻、滚动目标姿态角，以及可成像总时长的成像时域确定。再进行多条带拼接成像规划：由成像开始时刻及姿态偏置要求确定条带拼接方向，计算图像拼接点位置参数；根据满足载荷成像最大允许俯仰姿态机动角和姿态机动速度，确定相邻次成像开始时刻卫星位置与姿态机动开始时间；由成像时刻的轨道位置、前后摆俯仰姿态角、图像拼接点位置及侧摆成像偏流角计算相邻次成像滚动目标姿态；根据确定的滚动、俯仰目标姿态角和成像位置迭代计算偏流角，确定偏航目标姿态。给出了相应的单次侧摆成像路径和最大面积多条带拼接成像路径的自主规划计算流程。仿真结果表明：该方法能根据卫星姿态机动能力、轨道参数及载荷视场角自主完成成像条件分析及路径规划，实现载荷对目标区域无盲区最大幅宽成像，提高成像效率及卫星在轨任务自主规划执行能力。

光学遥感卫星； 宽幅成像； 路径自主规划； 多条带拼接； 侧摆成像； 目标姿态； 成像开始时刻； 成像结束时刻

0 引言

遥感载荷在提高图像分辨率后，成像幅宽一般会相应减小，采用多条带拼接成像的方式可增大成像物面覆盖率，弥补因幅宽减小导致成像覆盖面积变小的缺陷，提高卫星对特定目标区域的侦测能力。实现成像条带无缝拼接需要根据卫星的轨道位置、姿态机动能力(最大姿态机动角、机动速度)，以及目标区域位置规划计算卫星短时间内多次姿态机动的路径。传统采用地面计算再遥控上注的方式耗费大量人力物力，由于在轨卫星数量的增加和任务需求的变化，现有条件已不能满足要求。同时，因地面遥控站分布有限，在某些时段会出现不满足将卫星控制参数及时遥控上注的条件。实现对给定目标区域的多条带拼接成像路径自主规划计算，可显著减少地面处理工作量，同时保证满足成像条件的工作弧段不被遗漏。国内外对此进行了相关研究。美国2009年10月6日发射的WorldView-2卫星和法国2011年12月17日发射的Pleiades 1卫星均已利用姿态机动实现多条带拼接成像，大幅提高了遥感图像采集效率，但未知其成像路径自主规划的状况[1-2]。国内关于条带拼接成像多针对载荷技术进行研究，对卫星成像控制路径计算主要在地面进行，且鲜有关注针对给定区域无盲区且成像覆盖率最大化的目标[3]。

条带拼接成像路径自主规划任务，就是根据卫星的姿态机动能力、准确的轨道参数，以及目标区域中心位置，自主完成载荷成像前的卫星状态设定，包括卫星目标姿态、姿态机动开始时刻、成像开始时刻及成像时长等相关要素确定[4]。最大限度提高多次成像后的地面目标区域覆盖率或实现对特定目标区域的重复成像，实现对指定区域宽幅成像及区域内无盲点探测的目标，解决成像幅宽与图像分辨率间的矛盾。条带拼接成像任务自主规划的要点在于根据相关约束模型找到任务可执行时空域，确定拼接点位置。其难点在于如何基于有限的星载资源建立合适的递推模型及方案效益评估模型，保证任务规划的时效性，拼幅间无盲区及成像效益最优[5]。本文采用任务执行条件时空广域粗搜索和临近执行阶段二次精确规划计算结合的方法，解决复杂计算与星载资源约束间的矛盾，有利于星上自主执行。

1 目标任务可执行时空域搜索及确定

成像路径自主规划首先需通过位置关系递推计算判断成像时机，确保任务规划的时效性。其过程为递推计算目标与卫星在指定弧段内的距离及相应的时间点，然后结合载荷成像幅宽，姿态机动能力判断该时刻是否满足对目标成像的条件，确定任务可执行时空区间及目标姿态等任务执行相关技术参数[6]。

1.1 变量定义

设卫星距星下点轨道高度为H；卫星与地心间的距离为H0；地球平均半径为Re；卫星轨道角速度为ωo；卫星本体相对轨道坐标系的欧拉姿态角为φ，θ，ψ；垂直于载荷成像方向的等效视场半角为α0；载荷光轴与卫星地心连线矢量的夹角为α；满足载荷成像要求的最大滚动、俯仰姿态角分别为φmax，θmax；垂直于载荷成像方向的等效视场半角母线为l1，l2，两者与载荷光轴的夹角均为α0。

1.2 卫星对目标点成像时空关系条件

成像时卫星与目标点位置关系如图1所示。

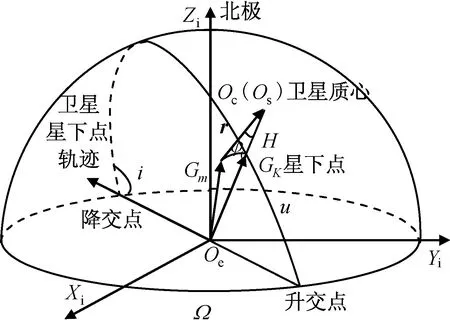
图1 成像时卫星与目标点位置关系

令卫星星下点至目标点方向矢量为rkm，载荷成像推扫方向矢量在地心惯性坐标系中可表示为rcx，则在仅有滚动姿态偏置条件下，载荷成像推扫到目标点时，目标点与星下点位置满足关系

(1)

反之，根据成像时刻目标点与卫星星下点的位置关系，不考虑偏流角需求，成像时刻滚动姿态φ0需满足关系

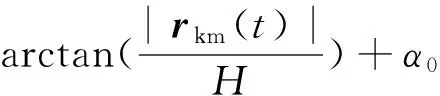
(2)

(3)

1.3 侧摆成像路径自主规划计算流程

若当前时刻地心惯性坐标系中目标中心点D的位置矢量rGm(t0)、卫星位置矢量rp(t0)、星下点位置矢量rGk(t0)已知，则根据载荷视场α0、姿态机动能力，对目标成像路径规划计算流程如下[4、7]。

a)计算卫星星下点至目标点方向矢量

(4)

b)计算地心惯性坐标系中卫星星下点轨迹沿卫星飞行方向的矢量

rcx(t0)=Rz(u(t0)+π/2)Rx(i(t0))×

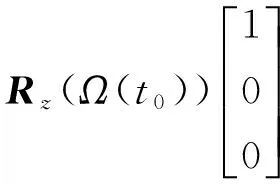
(5)

c)计算卫星星下点与目标点位置关系

(6)

d)判断位置关系是否满足成像条件

(7)

式中：βmax为卫星最大允许侧摆角；αmax为可容忍的位置关系确定误差阈值；u为轨道幅角；i为轨道倾角；Ω为升交点赤经；Rx，Rz分别为绕x、z向的方向余弦矩阵。

当条件d)不满足时，递推1个时间步长之后的卫星轨道及目标点位置矢量，重复步骤a)～d)直至在本圈一定弧段内找到满足式(7)的时间t。相应βkm(t)即为本圈对目标侧摆成像的滚动目标姿态角绝对值。成像路径规划结果为

a)姿态机动开始时刻：tj=tkT-Tj-ΔT1。

b)成像开始时刻：tc=tkT-ΔT1。

c)成像结束时刻：tm=tkT+ΔT2。

d)滚动目标姿态角

式中：Tj为完成姿态机动所需时长；tkT为卫星在轨位置满足式(7)的开始时刻；ΔT1，ΔT2分别为任务要求相对目标中心点之前和之后的成像时间长度，两者之和为单条带总成像时长。在多条带拼接成像过程中，ΔT1，ΔT2取决于成像目标区域长度要求和载荷成像最大允许偏置角，而单条带无拼接成像时长则与姿态机动能力无关。假定成像需要覆盖区域长度为L，则单条带成像总时长可表示为

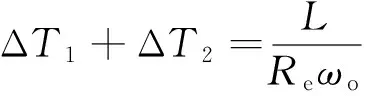
(8)

偏航姿态角ψ0由载荷偏流角控制精度需求决定，滚动侧摆成像时俯仰目标姿态角θ0为0。若在一定弧段内找不到满足条件d)的位置点，则停止本圈搜索，在卫星下一圈某弧段择机再次开始计算[8]。

2 多条带拼接成像路径自主规划

载荷对目标区域多条带拼接成像路径自主规划在单次侧摆成像路径自主规划的基础上完成。根据侧摆成像路径自主规划计算流程完成单次侧摆成像规划后，由成像开始时刻tc及姿态配置情况确定条带拼接方向，计算图像拼接点位置参数。然后根据满足载荷成像最大允许俯仰姿态机动角θmax、姿态机动速度，确定相邻次成像开始时刻卫星的轨道位置和姿态机动开始时间。再根据成像时刻的轨道位置、前后摆俯仰姿态角、图像拼接点位置及侧摆成像偏流角，计算相邻次成像滚动目标姿态。最后根据确定的滚动、俯仰目标姿态角及成像位置计算偏流角，确定偏航目标姿态。

2.1 条带拼接点位置确定

根据已知的侧摆成像路径计算条带拼接点，在条带边缘处实现拼接，可保证拼接物面幅宽最大化。令载荷成像光路矢量l1，l2与卫星地心连线的夹角分别为α1，α2；D1，D2为图像物面面拼接点，如图2所示。则α1，α2与卫星当前位置及姿态满足关系

cosα=cosφcosθ；

(9)

cosα1=sinα0(sinψsinθcosφ+

cosψsinφ)+cosα0cosθcosφ；

(10)

cosα2=-sinα0(sinψsinθcosφ+

cosψsinφ)+cosα0cosθcosφ.

(11)

因此，物面拼接点D1，D2与卫星的距离分别为

|rD1p|=H0cosα1-

(12)

|rD2p|=H0cosα2-

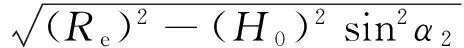
(13)

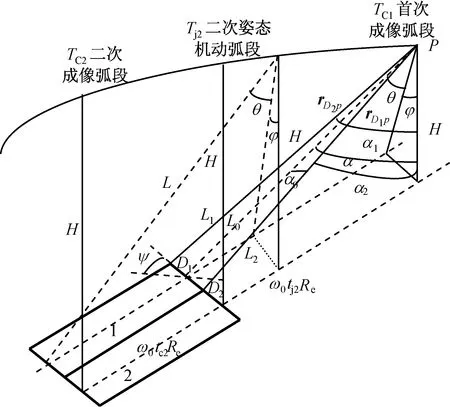
图2 成像时卫星位置姿态与地面物点位置关系Fig.2 Relation of satellite’s position andattitude with image area

根据卫星位置和姿态角可求出惯性系中成像光路矢量l1，l2分别为

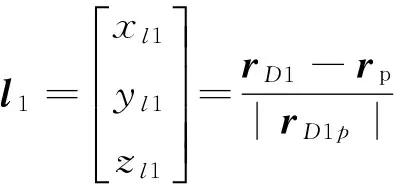
(14)

(15)

因此，成像时条带拼接点在地心惯性坐标系中的位置矢量rD1，rD2分别为

rD1=|rD1p|l1+rp；

(16)

rD2=|rD2p|l2+rp.

(17)

式中：rp为卫星在地心直角惯性坐标系中的位置参数，由轨道参数求得。

在图2所示的图像拼接顺序中，两次成像条带在地固坐标系中实现无盲区最大面积拼接，则第一次成像时光路l2对应的物点为第二次成像时光路l1对应的物点。

2.2 基于拼接点的目标姿态确定

目标姿态确定是在俯仰目标姿态已知，并假定条带间偏航目标姿态变化量小的条件下按式(18)～(21)求解滚动姿态，然后根据滚动、俯仰姿态及目标位置重新计算偏航姿态[9-10]。若偏航姿态较侧摆成像偏航姿态变化大，则需代入新求出的偏航姿态，重复式(18)～(21)求解滚动目标姿态[11]。

对拼接点成像时刻卫星至图像拼接点的方向矢量

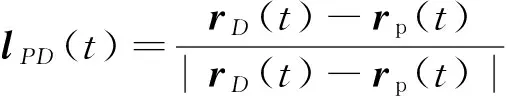
(18)

根据图像拼接顺序可确定载荷光路矢量。当第二次成像条带在第一次成像条带的右侧时，即滚动目标姿态需要增大，由图2可知：光路l1对应卫星至拼接D2的光路矢量，即lPD2(t)，否则，光路l2对应卫星至拼接点D1的光路矢量，即lPD1(t)，可同时计算出卫星至两可能拼接点的方向矢量后，再根据拼接方向选择。成像光路矢量在轨道坐标系中可表示为

Rz(u(t))Rx(i)Rz(Ω)lPD(t)；

(19)

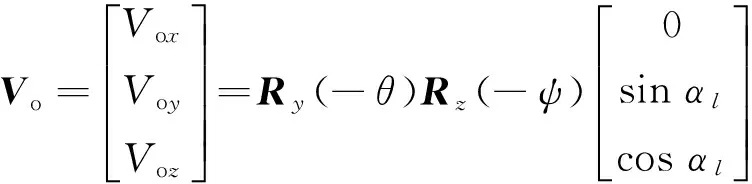
(20)

式(20)中：若l1为对拼接点的成像光路，则αl为α0；若l2为对拼接点的成像光路，则αl为-α0。首次迭代计算时，ψ为相邻条带成像时的偏航姿态角。

则待拼接条带的滚动目标姿态角(1-2-3转序)为

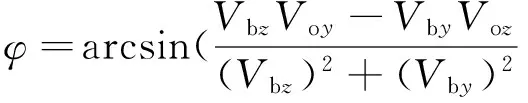
(21)

2.3 条带拼接成像开始时刻及时长确定

显然，在多条带拼接成像过程中，如各成像条带长度保持一致，像面条带长度就与卫星姿态机动速度及俯仰机动角θmax有关。根据图2所示姿态位置关系，成像时长ΔT与卫星轨道及姿态角关系可表示为

(22)

侧摆角φ0由目标位置和载荷有效视场决定。显然，前后摆角度越大，可成像时间就越长。

2.4 最大面积多条带拼接成像路径自主规划流程

多条带拼接成像路径规划是基于侧摆成像路径规划的，即先完成侧摆成像的路径规划，再根据侧摆成像路径参数规划前侧摆(一定的滚动姿态和正的俯仰姿态偏置)成像和侧回摆(一定的滚动姿态和负的俯仰姿态偏置)成像路径参数。自主规划计算流程如下。

a)根据侧摆成像路径自主规划计算流程完成侧摆成像路径规划，确定侧摆成像姿态机动开始时刻tj0，成像开始时刻tc0，成像结束时刻tm0，姿态偏置角φ0，ψ0，而θ0取0。

b)单条带成像时长确定

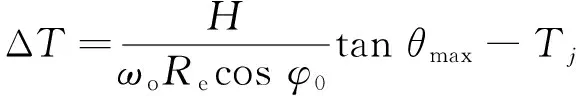
c)各拼接条带成像时间确定

(a)前侧摆成像条带：姿态机动开始时刻tj1=tc0-2Tj-ΔT；成像开始时刻tc1=tc0-ΔT-Tj；成像结束时刻tm1=tc0-Tj。

(b)侧回摆成像条带：姿态机动开始时刻tj2=tc0+ΔT；成像开始时刻tc2=tc0+ΔT+Tj；成像结束时刻tm2=tc0-2ΔT-Tj。

d)拼接条带目标姿态确定

(a)根据条带拼接点位置确定计算侧摆成像给出的拼接点rD1(tc0)，rD2(tc0)位置。

(b)计算对拼接点成像时拼接点位置rD1(tc1)，rD2(tc1)，rD1(tc2)，rD2(tc2)。

(c)根据条带拼接方向确定拼接点，按式(19)～(21)计算公式确定拼接成像滚动目标姿态φ1，φ2。

由此确定前侧摆成像目标姿态角(φ1，θmax)，侧回摆成像目标姿态角(φ1，-θmax)。

(d)根据偏流角要求计算偏航目标姿态ψk[12]。

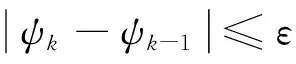
3 仿真

以3条带拼接成像路径规划为例。假定载荷光轴沿卫星偏航轴对地安装，3次成像姿态路径依次为前侧摆、侧摆和侧回摆的方式。设仿真条件为：卫星轨道参数，北京时间2014年3月7日10：27：9，半长轴7 500km，轨道倾角100°，偏心率0，升交点赤经187°，轨道幅角145°；姿态机动能力，滚动、俯仰姿态机动角度最大±40°，姿态机动速度40 (°)/50s；载荷，星下点成像幅宽200km；目标点中心位置，经度121°，纬度28°。不考虑偏流角姿态需求，设定偏航姿态-3.7°，自主规划计算结果如下。

a)第一种路径规划方案

首次成像开始时间10：27：49，目标姿态角为滚动-13.349°，俯仰40°；第二次成像开始时间10：30：37，滚动、俯仰目标姿态均为0°；第三次开始成像时间10：33：25，滚动姿态角13.326°，俯仰姿态-40°。

b)第二种路径规划方案

首次开始成像时间为13：27：49，目标姿态角滚动7.421°，俯仰40°；第二次开始成像时间13：30：37，滚动、俯仰目标姿态为0°；第三次开始成像时间13：33：25，滚动目标姿态为-7.412°，俯仰-40°。

根据以上路径规划结果，拼接成像效果分别如图3、4所示。图中：红色实线为载荷光轴景物点地面轨迹；蓝色阴影区域为成像物面。

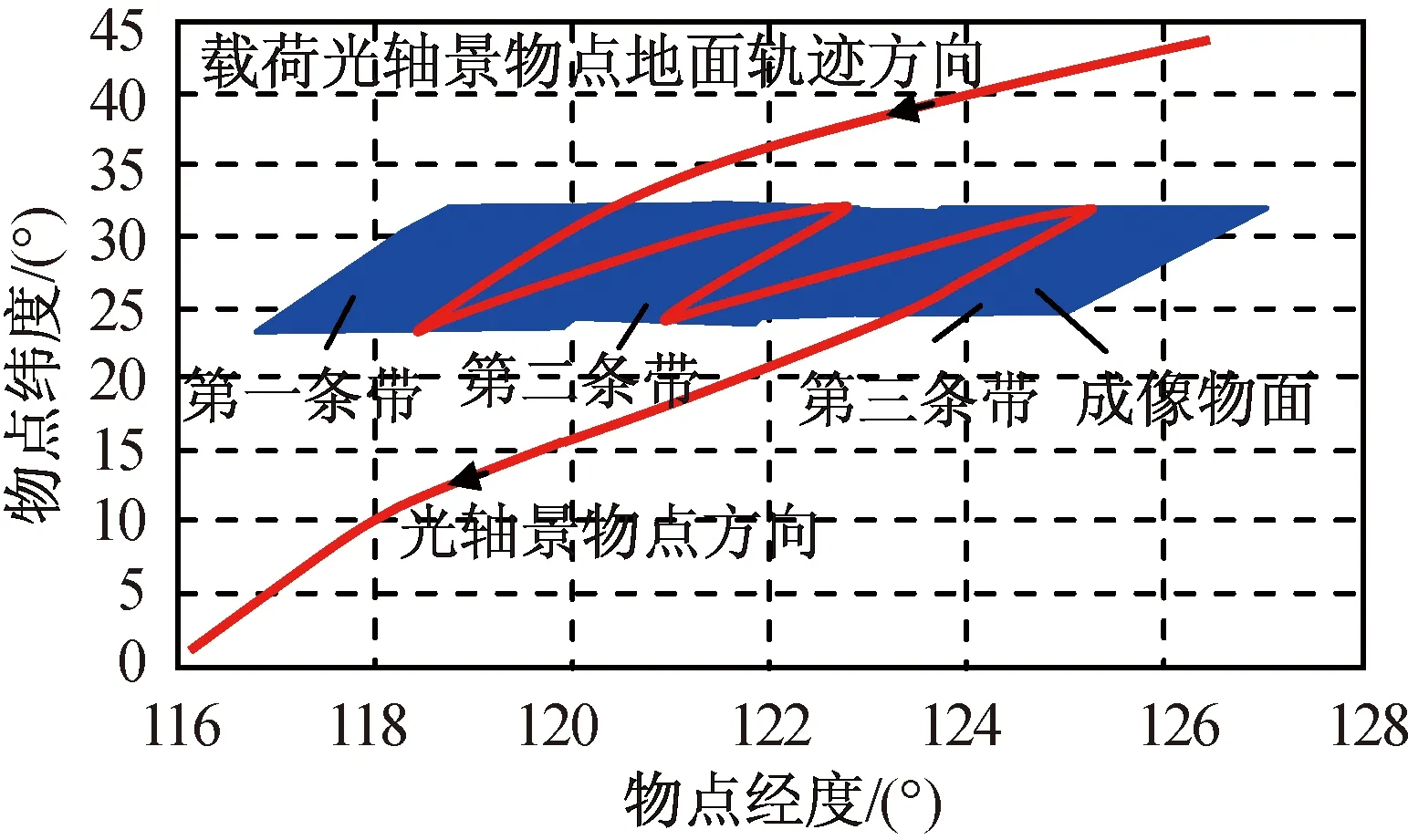
图3 第一种路径规划拼接成像效果图Fig.3 The first kind of image mosaic method’s effect

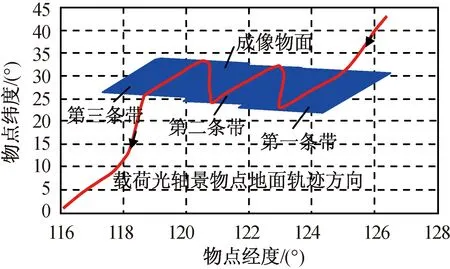
图4 第二种路径拼接成像效果图Fig.4 The second kind of image mosaic method’s effect

仿真结果表明：成像路径自主规划计算方案能实现拼接点附近的最大幅宽无盲区覆盖。因目标点与卫星相对关系为时变，故条带拼接顺序不同，则相应的姿态偏置角各异。在远离拼接点时，第一种仿真结果出现了狭小重叠区域，第二种仿真结果出现了狭小盲区。因此，在成像姿态路径规划过程中，需要根据目标区域位置及成像方向适当调整滚动目标姿态，并根据调整后的滚动、俯仰目标姿态计算偏航目标姿态，保证载荷清晰成像对偏流角控制精度要求。

4 结束语

本文对一种遥感卫星宽幅无盲区拼接成像路径的自主规划方法进行了研究。采用多条带拼接成像路径规划算法能根据载荷视场范围、卫星轨道参数及姿态机动能力自主完成对给定目标区域实施成像的指令编排，包括给出各成像条带对应的目标姿态角、姿态机动开始时间、成像开始时间等要素。仿真结果表明：该算法能实现遥感载荷对目标区域无缝隙宽幅拼接成像，弥补高分辨率载荷幅宽减小导致像面横向覆盖宽度减小的缺陷，提高卫星对指定目标区域的侦测能力。该算法同样可完成对目标区域的单圈多次重复成像路径自主规划，为实现区域内目标动态特性识别提供条件。规划计算过程仅需用户输入目标中心区域的经纬度位置及拼接要求即可，无需用户获知轨道位置、姿态机动能力等卫星相关参数，显著降低了地面操作的复杂程度。本文的多条带拼接成像路径规划基于拼接点位置预估，对

于动态推扫成像，即载荷成像时卫星绕俯仰轴以多倍轨道角速度进行姿态机动的成像路径规划，还需引入物面推扫速度变量。显然，推扫速度不一样，成像时间区间和偏航轴目标姿态均不一致。本文主要阐述单星多条带拼接成像任务自主规划问题，后续将展开对多星协同多条带拼接成像任务规划，动态多任务规划等方面的问题研究。

[1] RYE G D, COX S M. OrbWiew2, 3 and 4[J]. SPIE, 2003, 4881: 660-668.

[2] JONSSON F J, MORRIS A. Planning and scheduling for fleets of Earth observing satellites[C]// Proceeding of the International Symposium on Artificial Intelligence, Robotics and Automation in Space. Ottawa: [s. n.], 2001: 1-8.

[3] 张新伟. 敏捷遥感卫星工作模式研究[J]. 航天器工程, 2011, 20(4): 32-38.

[4] FUKUNAGA A. ASPEN: a framework for automated planning and scheduling of spacecraft control and operations: Proceedings of the International Symposium on AI, Robotics and Automation in Space[C]// Tokyo: 1997.

[5] 朱战霞, 杨博, 袁建平. 人工智能在卫星任务规划中的应用[J]. 飞行力学, 2008, 26(2): 79-81.

[6] 张正强, 陈英武, 谭跃进. 航天器自主规划问题的建模研究[J]. 计算机仿真, 2007, 24(4): 15-18.

[7] 徐瑞, 徐晓飞, 崔平远. 基于时间约束网络的动态规划调度算法[J]. 计算机集成制造系统—CIMS, 2004(2): 1-4.

[8] CHIEN S, SMITH B, RABIDEAU G, et al. Automated planning and scheduling for goal-based autonomous spacecraft[J]. Intelligent System, 1998, 13(5): 50-55.

[9] 袁孝康. 星载TDI-CCD推扫相机的偏流角计算与补偿[J]. 上海航天, 2006, 23(6): 10-13.

[10] 闫得杰. 飞行器姿态对空间相机像移补偿影响[J]. 光学精密工程, 2008, 16(11): 2199-2203.

[11] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.

[12] 景泉. 敏捷卫星偏流角计算模型研究[J]. 航天器工程, 2012, 21(4): 16-20.

An Auto Route Programming Method Research for Satellite’s Multi-Bar Image Mosaic Technology with Biggest Breadth and No Blind Area to Target

TANG Wen-guo1, 2, ZHANG Guo-yun3, ZHU Qing-hua1, 2, XU Xian-feng1, 2

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China;3. Xi’an Satellite Control Center, Xi’an 710043, Shannxi, China)

To solve the low size of detected area, low work efficiency and complicacy in operation of space camera with narrow field of view, an auto route programming method for satellite’s multi-bar image mosaic technology was studied in this paper. The first step was auto route programming a single side-sway imaging. The imaging route which included maneuvering start time, imaging start time, imaging end time, roll angle and single bar imaging time was programmed through judging position relationship of target area and satellite. The second step was multi-bar image mosaic programming. The mosaic direction was decided by imaging start time and attitude. The position parameters of image mosaic point were calculated. The satellite position and maneuvering start time of the next imaging were determined by the maximum allowable pitch angle and attitude maneuvering velocity. The roll angle of the next imaging was computed through orbit position, pitch angle of front and back sway, position of image mosaic point and side-sway drift angle. The drift angle was calculated according to the roll angle, pitch angle and imaging position. The yaw angle was set. The relative auto programming flowcharts of the single side-sway imaging route and multi-bar image mosaic imaging route with the biggest breadth and no blind area to target were given. The simulation results show that the multi-bar image mosaic technology proposed can accomplish the analysis of image condition and route programming by spin and maintenance of satellite attitude at the right point in right time. The arithmetic achieves programming automatically for imaging route having the biggest breadth with no blind area based on evaluation of the relative position of the satellite and target when the load’s field of view and the satellite’s slew ability are considered.

Optical remote satellite; Wide regional imaging; Auto route programming; Multi-bar image mosaic; Side-sway imaging; Target attitude; Imaging start time; Imaging end time

1006-1630(2016)06-0061-06

2016-04-30：

2016-06-10

唐文国(1979—)，男，高级工程师，主要研究方向为航天器导航、制导与控制。

V448.21

A

10.19328/j.cnki.1006-1630.2016.06.008