基于四元数的偏流角跟踪与条带拼接成像研究

杜 宁,王世耀,孟其琛

(上海航天控制技术研究所,上海201109)

基于四元数的偏流角跟踪与条带拼接成像研究

杜 宁,王世耀,孟其琛

(上海航天控制技术研究所,上海201109)

根据小卫星星载相机存在后视角或安装相机摆镜导致相机实际光轴无法与星体主轴平行的状况，为避免用欧拉角时的姿态解算与转序问题，提出了一种基于四元数的卫星偏流角跟踪与条带拼接成像姿态控制方法。用四元数描述卫星姿态，根据相对轨道系目标四元数，绕相机光轴转动偏流角，以此作为成像模式目标四元数，实现绕空间轴的偏流角跟踪控制。给出了姿态规划算法：固定偏置姿态确定偏流角跟踪后的目标姿态和目标角速度，用迭代法提高偏流角控制精度，并在姿态机动过程开始即进行偏流角跟踪，保证姿态机动到位和高精度偏流角跟踪的同时实现。基于内干扰力矩前馈方法设计了姿态机动控制律。以同轨双条带拼接成像为例，给出了成像控制方法：在对日或对地定向基础上，计算偏置目标姿态和目标角速度，并调用姿态机动控制算法；姿态机动到位后，若需当轨完成多目标姿态机动，则用姿态机动控制算法保持姿态偏置飞行和偏流角跟踪控制。数学仿真结果验证了该算法的有效性和高精度。

时间延迟积分电荷耦合器件(TDI-CCD)相机； 后视角； 偏流角跟踪； 条带拼接成像； 立体成像； 姿态规划； 四元数； 姿态机动

0 引言

星载相机系统在实现高分辨率的同时，为降低难度其视场角较小，导致地面覆盖宽度往往也较小。因此，利用卫星高速的姿态机动能力，快速改变相机的对地指向，快速高效地获取所需的非星下点目标遥感数据，成为当今世界商业遥感卫星的一个发展方向。通过卫星平台大角度快速姿态机动，能使星载相机实现同一轨道弧段内对多个目标的成像观测，因此可显著提升相机载荷的使用效率。利用卫星平台绕俯仰轴、滚动轴的快速姿态机动能力，配合相机推扫成像，可实现同轨内成像幅宽拼接功能，一定程度避免相机幅宽对成像幅宽的限制。同样，卫星在姿态控制稳定度具备了相应能力后，可采用姿态机动过程中的扫描成像方式，大幅提高图像覆盖能力。随着遥感数据应用的快速发展，获取地面目标的三维信息成为一种新的市场需求。通过控制星体俯仰轴的快速姿态机动，单台相机也可实现对同一地物的短时间内不同角度观测，以满足立体观测需求，避免安装多台相机，能降低卫星的经济成本和研制难度。综上所述，利用敏捷技术实现姿态的灵活指向，可实现四种典型工作模式，主要包括同轨多目标成像模式、同轨多条带拼接成像模式、同轨立体成像模式和动态扫描成像模式等[1-3]。文献[1]仅对提高相机使用效率的成像模式进行了初步分析；文献[2-4]仅对商业遥感卫星成像模式和技术指标进行了介绍，上述文献均未涉及具体的卫星姿态控制算法。文献[5]对相机光轴沿星体Z轴的理想情况，推导了摆动成像过程的粗略欧拉角姿态；文献[6-7]介绍了单目标姿态成像过程的偏流角计算和补偿方法，上述文献基于欧拉角描述姿态，偏流角补偿精度不高，且不适于复杂成像模式。文献[8]单纯介绍了偏流角计算方法，未设计偏流角补偿；文献[9-10]介绍了敏捷卫星姿态机动算法，但未涉及偏流角跟踪问题。综上对具体的条带拼接等成像模式，相关文献并未给出具体姿态规划与姿态控制方法。

对同轨多目标成像、同轨多条带拼接成像或立体成像，就卫星姿轨控分系统而言，都需解决相机光轴任意指向时的偏流角计算与姿态规划、姿态快速机动、姿态偏置后的快速偏流角跟踪等共性问题。其中同轨双条带拼接成像最具代表性，在该控制模式基础上，修改目标偏置姿态和机动起止时间，即可实现同轨多目标成像和立体成像模式。因此，本文以双条带拼接成像为例，对偏流角跟踪和姿态控制方法进行了研究，先用四元数描述偏流角跟踪问题，并基于迭代方法推导了姿态规划算法，基于内干扰力矩前馈方法设计了姿态机动控制律。

1 偏流角控制的四元数描述

偏流角的定义是目标在像平面投影的像移速度矢量与推扫阵列的列向夹角。对TDI-CCD相机等以推扫方式工作的有效载荷，为保证其成像清晰，要求卫星姿轨控分系统通过姿态控制实时调整载荷的视轴，使成像目标在像平面的移动速度矢量方向垂直于推扫阵列。此即为卫星姿轨控分系统偏流角跟踪控制(偏航导引)要求。

相机偏流角与卫星轨道、姿态、角速度，相机焦距和后视角等参数相关。卫星在轨飞行过程中，根据标称姿态规划出偏流角后，跟踪该偏流角到位时，新的姿态和角速度又将对应新的偏流角。因此，高精度偏流角计算与控制必须根据星体轨道和姿态参数实时计算，具体计算方法可参考文献[8]。

相机成像坐标系如图1所示。图中：C系为相机坐标系；P系为像面坐标系。偏流角计算原理如图2所示。图2中：Ret为从地心指向目标T的矢量；Res为从地心指向卫星质心Os的矢量；Rst为从卫星质心Os指向目标T的矢量；Rct为从C系原点指向目标T的矢量；Rpi为像平面系中像点位置。

图1 相机成像坐标系Fig.1 Imaging coordinate system of camera

图2 偏流角计算原理Fig.2 Calculation of drift angle

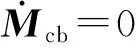
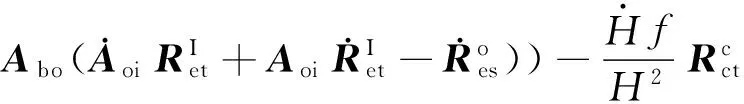
(1)

式中：H为相机至地面成像点的距离；Abo为卫星轨道系至本体系转换矩阵；Aoi为惯性系至轨道系转换矩阵。偏流角

(2)

以往常见的卫星相机光轴沿本体系Z轴，且不含摆镜，姿轨控修正偏流角，仅需绕本体系Z轴姿态偏置一定角度，该角度同偏流角即可，如图3所示。因此，相关领域的研究常用依次旋转三轴欧拉角的方式描述偏流角控制问题[4-5]。适于小卫星的相机，因尺寸与重量受约束，多采用离轴多次反射方法增大相机焦距，常见星载相机多存在一个后视角，即实际光轴不再沿相机和星体主轴，而是与星体+Z轴存在一固定夹角。此外，部分星载相机配置了相机摆镜，随着摆镜的运动，相当于2倍相机光轴角度变化。因此，星载相机的通用状况是实际光轴无法与星体主轴平行。姿轨控系统修正偏流角时，应绕瞬时的相机视场光轴方向偏置一定角度，此角度同偏流角。此时，卫星相当于绕空间轴姿态偏置，三轴姿态可能都有分量，如图3所示。此外，条带拼接等工作模式需要卫星平台通过任意目标的姿态机动调整相机光轴指向，在此基础上的偏流角跟踪控制将更为复杂。此时，若继续采用三轴欧拉角依次旋转的方式描述姿态控制问题，将带来姿态解算及转序问题，且姿态控制流程复杂。

图3 离轴相机后视角Fig.3 Rear-view angle of off-axis camera

针对上述情况，本文不再使用欧拉角，而是采用四元数描述偏流角跟踪控制问题。根据偏流角计算对应的基准姿态、相机偏流角和相机后视角，用四元数描述卫星目标姿态。具体为：在相对轨道系目标四元数qor0基础上，绕相机光轴转动偏流角β，以此作为成像模式目标四元数qor，有

(3)

式中：e为相机光轴单位矢量在卫星本体的分量，对后视角为θ，不含摆镜的相机

(4)

用四元数描述偏流角跟踪控制，避免了导引过程中目标姿态的任意性产生的控制转序问题，可在平台以任意姿态机动控制的基础上，进一步实现绕空间轴的偏流角跟踪控制。

2 条带拼接成像的姿态基准

以相机光轴接近星体+Z轴、1-2-3姿态转序为例，由于卫星前向飞行，典型的双条带拼接成像应由左前视(正滚动、正俯仰姿态)推扫成像+右后视(负滚动、负俯仰姿态)推扫成像实现，如图4所示。因卫星滚动或俯仰姿态偏置能增加成像幅宽，故双条带拼接成像宽度将明显大于相机星下点幅宽的2倍。

图4 双条带拼接成像Fig.4 Dual stripmap stitching imaging

以卫星轨道高度500 km、相机视场角34°为例，在星体三轴对地定向控制模式下，相机视场对应星下点成像幅宽约300 km。由于卫星滚动或俯仰姿态偏置能增加成像幅宽，为实现幅宽900 km拼接成像，可采用前视成像+后视成像模式。以前视姿态和后视姿态分别为[20.2° 37° 0°]，[-20.2° -37° 0°]为例，为保证推扫成像距离，要求控制星体在60 s内由前视姿态机动至后视姿态并稳定。

在卫星对地或对日稳定控制的基础上，均可直接通过姿态机动转至对地左前视推扫成像模式，在该模式下跟踪偏流角；左前视成像完成后，自主姿态机动至右后视推扫成像模式，并在成像完成后，自主返回稳定对地或对日定向控制模式。

基于四元数的姿态机动控制算法，可用于对日定向转成像目标姿态的机动，也可用于左前视姿态与右后视姿态间的姿态机动。调用姿态机动控制算法，只需在测量星体当前的相对轨道系姿态qob和角速度ωob基础上，明确目标姿态qor和目标角速度ωor即可。

以左前视成像为例，对应滚动姿态φA和俯仰姿态θA满足

(5)

结合实时的轨道信息，该标称姿态qorA0将对应标称偏流角βA0。根据偏流角跟踪控制原理，应在目标姿态基础上，绕相机光轴转过偏流角，以此作为成像模式目标姿态qorA，有

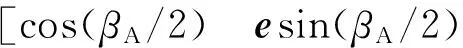
(6)

式中：e为相机光轴单位矢量在卫星本体的分量。

需注意：在转过标称偏流角后，星体新的姿态将对应新的偏流角，虽然此时偏流角实时计算结果已为小量，但对高精度偏流角控制，该误差不可忽略。

为进一步提高偏流角控制精度，采用迭代方法，每个控制周期重新计算目标姿态和目标姿态对应的偏流角，并在下一控制周期的目标姿态中转过该偏流角，直至最终目标姿态和角速度对应的偏流角接近0，即实现高精度偏流角控制。

目标姿态

(7)

对目标姿态微分可得目标角速度

(8)

式中：T为计算机控制周期；k为当前控制周期，k-1为前一控制周期。

右后视目标姿态的计算方法与左前视目标姿态计算一致。

至此，给出了固定偏置姿态考虑偏流角跟踪后的目标姿态和目标角速度。因在目标姿态的计算过程中始终考虑了偏流角跟踪，故在姿态机动过程开始即已进行偏流角跟踪，保证了姿态机动到位的同时，高精度偏流角跟踪也已实现。

3 姿态机动控制算法

为提高滚动姿态机动过程中的动态特性，可引入陀螺角速度信息；为实现任意姿态最短路径机动，以星体当前姿态与目标姿态偏差四元数作为姿态控制基准；进而以飞轮作为姿态控制执行机构，设计PD控制规律，机动过程对内干扰力矩进行前馈。

qrb=(qor)-1⊗qob；

(9)

(10)

卫星姿态动力学方程

(11)

式中：I为星体转动惯量；h为飞轮角动量；Mc，Md分别为控制力矩和环境干扰力矩。式(11)可变为

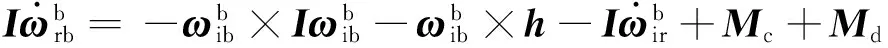
(12)

(13)

式中：qe为偏差四元数qrb的矢量部分；Kp为比例系数；Kd微分系数。

根据Lyapunov稳定性原理，设计的控制器对误差四元数和误差角速度来说是渐近稳定的[9-10]。具体控制过程为：在对日或对地定向基础上，计算偏置目标姿态和目标角速度，以此调用姿态机动控制算法；在姿态机动到位后，若需当轨完成多目标姿态机动(如双条带成像模式)，则保持姿态机动控制算法进行姿态偏置飞行和偏流角跟踪控制。

4 数学仿真

对相机载荷双条带拼接成像模式进行仿真，该模式包含了姿态机动和偏置成像控制。设卫星轨道高度483 km，轨道倾角30.5°；相机视场角34°，后视角8°，CCD尺寸3.510-6m；前后视目标姿态分别为[20.2° 37° 0°]，[-20.2° -37° 0°]；星敏三轴测量噪声[24″ 24″ 24″](3σ)；陀螺零偏3 (°)/h，陀螺随机游走系数0.005 (°)/h0.5；星体惯量[I1I2…I9](此处：I1=154 kg·m2，I2=1.6 kg·m2，I3=-2.7 kg·m2，I4=1.6 kg·m2，I5=153 kg·m2，I6=0.16 kg·m2，I7=-2.7 kg·m2，I8=0.16 kg·m2，I9=123 kg·m2)；飞轮最大角动量11 N·m·s，最大力矩1 N·m；机动过程限制星体最大角速度3 (°)/s。仿真中取初始姿态和角速度均为零，仿真开始即进行左前视姿态机动并跟踪偏流角，100 s时开始由左前视转至右后视姿态机动，机动到位后跟踪偏流角，仿真所得相对轨道系三轴姿态角、三轴姿态控制误差、相对轨道系三轴角速度、三轴角速度控制误差、偏流角规划误差、相机中心点实际偏流角，以及地面成像点经纬度分别如图5～11所示。

图5 相对轨道系三轴姿态角Fig.5 Three-axis attitude angle relative toorbit reference frame

图6 三轴姿态控制误差Fig.6 Control error of three-axis attitude angle

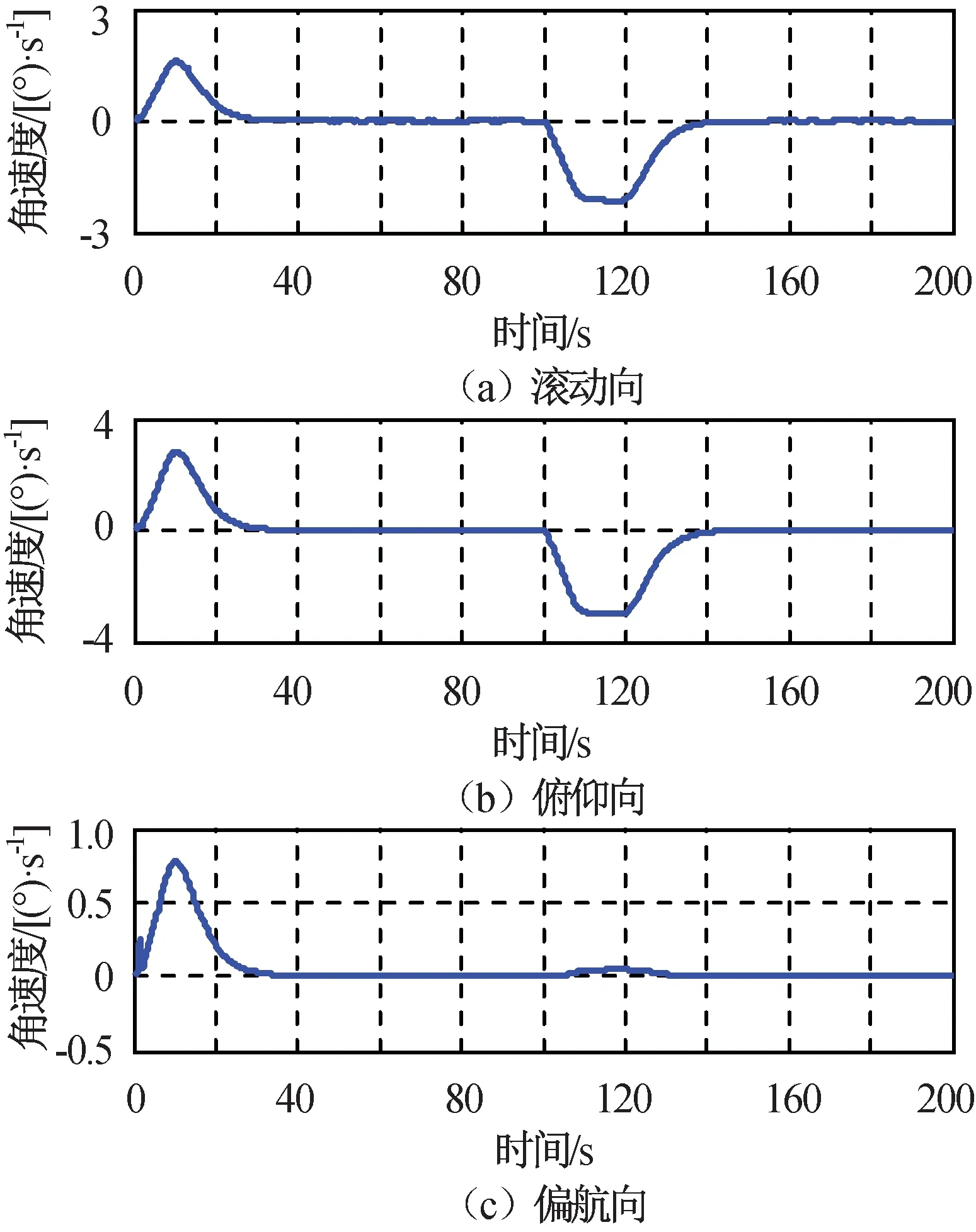
图7 相对轨道系三轴角速度Fig.7 Three-axial angular relative to orbit reference frame

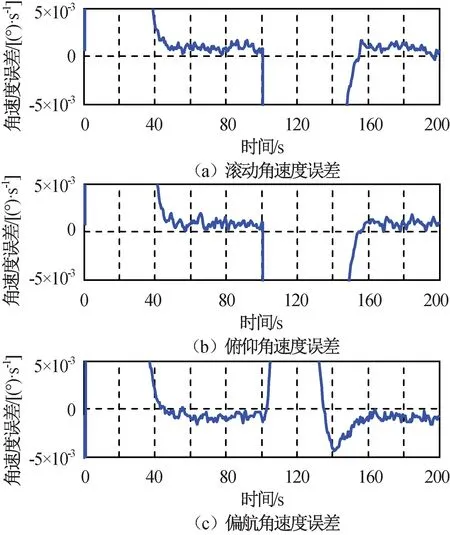
图8 三轴角速度控制误差Fig.8 Control error of three-axial angular

图9 偏流角规划误差Fig.9 Error of drift angle planning

图10 相机中心点实际偏流角Fig.10 Real drift angle at core point of camera

图11 地面成像点经纬度Fig.11 Latitude and longitude at earth imaging point

由仿真结果可知：通过姿态机动和偏置成像控制能当轨实现双条带成像，拼接后成像宽度大于900 km，公共成像距离大于300 km；由左前视转至右后视姿态机动时间小于60 s；推扫成像过程姿态控制误差峰峰值小于0.03°，角速度控制误差峰峰值小于0.002 (°)/s；前视和后视推扫成像过程中，相机中心点偏流角规划精度优于0.001°；由于姿态测量噪声引起了星体角速度误差，造成以动力学轨道和姿态参数解算的实际偏流角误差明显大于规划误差，在本文仿真条件下该误差峰峰值小于0.1°。

5 结束语

本文用四元数描述星载相机偏流角控制问题，设计了大角度快速机动和机动到位后快速跟踪偏流角控制算法，给出了姿态基准描述方法和姿态控制算法，实现了高精度双条带拼接成像控制。该方法能适应相机含后视角或含摆镜等通用载荷，并只需通过目标姿态设定，同样适于同轨多目标成像、立体成像等工作模式。该法通过多拍连续迭代算法提高了偏流角控制精度和软件运行效率。数学仿真结果验证了算法的有效性和高精度。与欧拉角描述偏流角跟踪方法相比，本文算法简单、精度高。后续将对卫星摆动过程成像控制进行研究。

[1] 张新伟, 戴君, 刘付强. 敏捷遥感卫星工作模式研究[J]. 航天器工程, 2011, 20(4): 32-38.

[2] LONGBOTHAM N, BLEILER C, CHAAPEL C, et al. Spectral classification of Worldview-2 multi-angle sequence[C]// IEEE GRSS and ISPRS Joint Urban Remote Sensing Event. Munich: IEEE Computer Society, 2011: 109-112.

[3] PERRET L, BOUSSARIE E, LACHIVER J M, et al. The Pléiades system high resolution optical satellite and its performance: Proceedings of the 53rdInternational Astronautical Congress[C]// Paris: Mario-Nikis, 2002.

[4] GIROUART B, SEBBAG I, LACHIVER J M. Performances of the Pleiades-HR agile attitude control system[C]∥ 5thESA International Conference on Spacecraft Guidance, Navigation and Control Systems. Frascati: ESA, 2003: 497-500.

[5] 黄群东, 杨芳, 赵键. 敏捷卫星宽幅动态成像姿态调整技术研究[J]. 航天器工程, 2013, 22(4): 17-22.

[6] 袁孝康. 星载TDI-CCD推扫相机的偏流角计算与补偿[J]. 上海航天, 2006, 23(6): 10-13.

[7] 谢少波, 丁丕满, 何赟晟, 等. TDI CCD遥感卫星对其他卫星成像的可行性分析[J]. 上海航天, 2015, 32(2): 28-31+53.

[8] 仲惟超. 航天器轨道和姿态参数对光学成像的影响分析[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[9] WIE B, WEISS H, ARAPOSTATHIS A. Quaternion feedback regulator for spacecraft eigenaxis rotations[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(3): 375-380.

[10] THIEUW A. Pleiades-HR CMGs-based attitude control system design, development status and performances[C]// 17thIFAC Symposium on Automatic Control in Aerospace, ACA′ 2007. Toulouse: [s. n.], 2007: 834-839.

Study on Drift Angle Tracking and Multistrip Mapping Stitching Imaging Based on Quaternion

DU Ning, WANG Shi-yao, MENG Qi-chen

(Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

According to optical axis of camera deviating from the body axis of satellite caused by the rear-view angle of spaceborne camera or tilt mirror setting for small satellite, a method of drift angle tracking and multistrip stitching imaging attitude control based on quaternion was proposed in this paper, which could avoid the attitude computation and rotation sequence problems using Euler angle. The satellite attitude was described by quaternion. According to the target quaternion of relative orbit coordinate system, it rotated the drift angle around optical axis of camera which was served as the target quaternion for imaging. The drift angle tracking around space axis was implemented. The attitude planning algorithm was given. The target attitude and angular velocity after the drift angle tracked were determined when the offset attitude was fixed. The control accuracy of the drift angle was improved by iteration method. The attitude maneuvering and high precision drift tracking were implemented at the same time by tracking the drift angle while maneuvering. The attitude maneuver control algorithm was designed based on inner disturbance moment forward feedback. The imaging control method was given for the example of same orbit dual stripmap imaging. The offset target attitude and angular velocity were calculated based on orientation to the sun or the earth. The attitude maneuver control algorithm was used. After maneuvering finished, the attitude maneuver control algorithm would be used for keeping offset flying and drift angle tracking if it need multitarget maneuver in one orbit. The numerical simulation results proved effectiveness and high precision of the algorithm proposed.

Time delay and integration charge-coupled device (TDI-CCD) camera; Rear-view angle; Drift angle control; Multistrip mapping stitching imaging; Stereo imaging; Attitude planning; Quaternion; Attitude maneuver

1006-1630(2016)06-0031-07

2016-06-16；

2016-07-22

杜 宁(1985—)，男，硕士，主要研究方向为卫星GNC分系统设计。

V448.21

A

10.19328/j.cnki.1006-1630.2016.06.004