基于伪谱同伦算法的编队飞行任务设计研究

岳晓奎,段 逊

(1.西北工业大学 航天学院,陕西 西安 710072; 2.西北工业大学 国家飞行动力学重点实验室,陕西 西安 710072)

基于伪谱同伦算法的编队飞行任务设计研究

岳晓奎1、2,段 逊1、2

(1.西北工业大学 航天学院,陕西 西安 710072; 2.西北工业大学 国家飞行动力学重点实验室,陕西 西安 710072)

针对编队飞行中多个从星飞行任务设计问题，研究了用伪谱同伦算法对其进行优化的方法，以获得小推力时的最省燃料转移轨道。将无推力的转移轨道作为初始轨道，用伪谱法对其进行优化，使其转移轨道能量最优，所得轨道可作为初值，解决了同伦算法对初值敏感的问题。再用同伦算法进行优化，降低了间接法求解最优控制问题的难度，得到最省燃料轨道，解决了求解Bang-Bang控制产生的不光滑性。对运行于高度400 km近地圆轨道上3颗完全相同的从星算例进行了求解，构建轨道跟飞/领飞构型的最省燃料轨道。结果表明：伪谱同伦算法能较大幅度节省燃料，对求解编队飞行从星转移轨道设计可行且有效。

编队飞行； 轨道转移； 伪谱同伦算法； Bang-Bang控制； 伪谱法； 同伦法； 最省燃料； 小推力

0 引言

卫星编队是指由物理上分离但彼此相互合作从而共同实现同一空间任务的一系列卫星(特别是小卫星)所组成的空间系统[1]。编队飞行中的每颗卫星在共同保持一个特定的队形时，还受到引力场(如太阳、各大行星、月球等)的影响。在编队飞行过程中，每颗卫星相互联系、协同工作，共同完成任务。与单颗卫星相比，多颗卫星组成的编队具可提高系统性能和降低成本等优势。卫星编队飞行是现代小卫星一种新的应用模式，小卫星的重大缺陷是能携带的燃料较少，因此规划燃料最优轨道成为编队飞行中亟待解决的问题。当空间任务发生变更，卫星编队构型需相应变化，在原构型的基础上建立新的相对运动形式是卫星编队飞行的重大问题。轨迹优化在空间飞行探索中不断发展，其理论是求解编队飞行构型重构的基础。当前，推进方式主要有大小推力两种形式。小卫星因携带燃料的较少，采取小推力方式居多，因此研究者在不断研究小推力的优化方法。在已报道的研究中，求解优化轨迹的数值方法主要有间接法、直接法和混合法三类[2-3]。直接法的要点是将控制变量或状态变量离散化，将原问题转换成一个非线性规划问题，其典型算法有伪谱法，其不足主要是未引入一阶最优必要性条件，不能保证得到的解是最优解。间接法是基于变分法或庞特里亚金极大值原理等最优控制理论，将小推力轨迹优化问题转化为最优控制问题的方法，如同伦算法，其最大缺点是初值很难猜测，且对初值及其敏感。因同伦法与伪谱法有很强的互补特性，组合应用既可解决初值敏感问题又能化解燃料最优问题中Bang-Bang控制引起的不光滑性困难，从而获得编队飞行中从星的燃料最优轨迹。为此，本文对一种基于伪谱同伦算法的编队飞行构型重构任务设计方法进行了研究。先基于大推力下的C-W方程，以获得一条大推力转移初始轨道，再用伪谱法，以性能最优为优化指标进行优化(因其无法解决Bang-Bang控制的不光滑性，故无法得到最省燃料轨道)，以获得一条平滑的控制曲线和小推力转移轨道。最后，以基于伪谱法得到的小推力转移轨道为初值再进行同伦算法优化，以获得最省燃料的小推力轨道和控制曲线。

1 问题描述

本文假设一颗主星携带3颗完全相同的从星运行于高度400 km的近地圆轨道，用这3颗从星构建同轨道跟飞/领飞构型，从而使燃料最省[4]。

为描述从星与主星(主星运行于圆轨道)间的相对运动，引入HCW坐标系，此命名仅针对后文中的Hill-Clohessy-Wiltshire(HCW)方程：原点O位于主星；Ox轴由地心指向主星；Oy轴在主星轨道面内与Ox轴垂直，沿运动方向为正；Oz轴垂直于轨道平面，与Ox、Oy轴构成右手坐标系，如图1所示。本文的运动状态变量均在HCW坐标系中表示。

图1 HCW坐标系Fig.1 HCW coordinate system

从星相对主星的线性化相对运动方程(HCW方程)可表示为

(1)

式中：x，y，z为从星相对主星的位置；n为主星的圆轨道角速度；Fx，Fy，Fz分别为施加于从星上的推力的坐标分量；m为从星的质量。考虑从星在轨道机动过程消耗的燃料质量相对其本身的质量来说相对较小，故认为从星的质量始终保持不变，式(1)中的m恒取为从星的初始质量50 kg。

(2)

式中：ge为地球海平面的重力加速度；F为推力幅值，且F=[(Fx)2+(Fy)2+(FZ)2]0.5；Isp为推进比冲，且Isp=1 000 s；Δt为连续推力的持续时间。

当Fx=Fy=Fz=0(即不施加任何推力)时，给定从星(相对主星)在初始时刻(t=0)的位置和速度为

HCW方程的解为

(3)

式中：n为主星的圆轨道角速度。将式(3)化为常值项、长期项与周期项之和的形式

(4)

式中：nt+φ为从星的相位差；

由式(4)可知：有界运动(无长期漂移项)的存在条件为xc=0，即

(5)

当b=0，c=0时，不存在周期项运动，此时的构型最简单，为同轨道领飞/跟飞相对轨迹，有

(6)

当yc>0时，称为领飞；当yc<0时，称为跟飞。3颗从星同轨道领飞/跟飞的目标构型如图2所示。图中：yc=-4，4，8 km。

图2 领飞/跟飞构型Fig.2 Fly/flight configuration

2 优化流程

2.1 伪谱法

伪谱法属于直接法中的配点法。直接法是将一个连续系统求解最优控制问题中的控制变量或状态变量离散化，从而进行求解非线性规划问题，最终获得原最优问题的较精确解。直接法可分为配点法和直接打靶法。直接打靶法一般是将控制变量进行离散化，而配点法一般将控制变量和状态变量均离散化，包括求积型配点法和伪谱法。直接法的优势是：不用推导最优性一阶必要条件，易建立最优轨道的非线性优化模型；对初值轨迹精度要求不高，无需猜测协态变量的初值，对优化参数的收敛域宽，易得到收敛解。其缺点是：不提供协态变量信息，不能保证获得的非线性规划的最优解是原最优控制问题的解；易收敛至某一个局部解，而非全局最优解[5-6]。

与其它配点法相比，伪谱法的最大差别是用数值微分方法近似其中的导数项(使用Lagrange插值全局近似，不基于有限差分的局部近似)，从而得到节点上的离散动力学方程(即残值表达式)[7-8]。

在一般的最优控制问题中，令状态变量x(t)∈Rn，控制变量u(t)∈Rn，初始时间t0，终止时间tf，t∈[t0，tf]。确定最优控制使性能指标能最优，即

(7)

满足以下条件：

a)状态约束

(8)

b)路径约束

C(x(t),u(t),t0,tf)≤0∈RC;

(9)

c)终端约束

φ(x(-1),t0,x(1),tf)=0∈Rq.

(10)

求解的步骤是采用庞特里亚金极小值原理求解其中的约束问题。直接法将连续最优控制问题离散并转为非线性规划问题进行求解。将归一化时间区间τ∈[-1，1]用全局多项式插值逼近最优控制问题的各变量，常用的全局多项式以拉格朗日多项式作为基函数，在τ∈[-1，1]选取插值点定义插值多项式M个，最优控制问题中的状态变量、控制变量可近似化为如下形式。

a)状态变量

(11)

式中：x(τ)为M-1阶多项式值；Li(τ)为拉格朗日多项式，且

(12)

b)控制变量

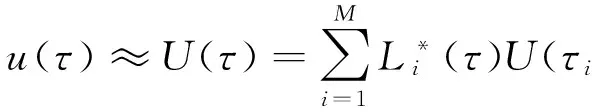
(13)

式中：U(τ)为离散点的控制量；

(14)

首先选取合适的多项式插值点，进而将最优控制系统中的协态变量、控制变量和状态变量等进行多项式逼近。同时，伪谱法选取合适的插值节点以对最优能量指标、约束条件、动力学等进行非线性约束。积分逼近的一般形式为

(15)

式中：τi为时间区间τ∈[-1，1]中M个离散的积分插值点；ωi为积分权重(k=1，…，M)。合理的积分离散点分布，对积分逼近精度的影响至关重要。

常用的伪谱法有Legendre伪谱法、Gauss伪谱法、Radau伪谱法和Chebyshev伪谱法，见表1。总体来说，选取的配点方法不同会导致出现差异。本文使用Radau伪谱法，选择的配点为Legendre Gauss-Radau(LGR)[9]。

表1 伪谱法插值基函数及配点类型

LGR点是通过求取多项式

PM(τ)+PM-1(τ)

(16)

的零点获得。此处：PM(τ)，PM-1(τ)为对应点上的值。积分权重为

(17)

本文采用小推力轨迹优化模型为

(18)

(19)

状态变量x=[rvm]T，系统模型可写成紧凑形式

则小推力优化问题以转换成求解最优轨迹x(t)和最优控制u(t)，满足初、末状态约束条件

(20)

和控制受限约束

‖u‖≤Tmax，

(21)

并使能量最优指标J取最小值，即

(22)

引入归一化时间τ∈[-1，1]，

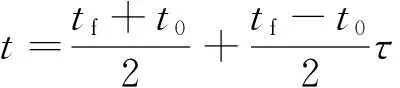
(23)

则轨迹优化方程可表示为

(24)

引入状态变量的Lagrange插值多项式

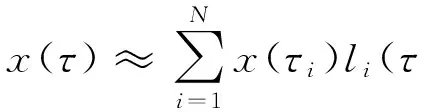
(25)

式中：li(τ)为Lagrange插值函数，包含LGR积分点和边界节点，且

(26)

状态变量x(τ)的导数可通过微分矩阵近似得到，即

(27)

同样，对控制变量引入Lagrange插值多项式

(28)

根据能量最优性能指标，经伪谱离散得

(29)

式中：N为选取点的个数；ωk为LGR积分点对应的权函数，且

(30)

2.2 同伦法

同伦法是间接法的一种。间接法是根据性能指标从而推导得到满足指标的协态变量方程、控制量、横截条件等，构成系统微分方程建立两点边值问题，然后选用合适的迭代算法求解出满足边界条件约束、开关控制约束和横截条件约束的最优轨道。间接法的优势是：无需直接对性能指标寻优，满足最优控制理论一阶必要条件的收敛解即被认为是最优轨迹；优化参数少，如协态变量初值较精准，就能快速得到收敛解。该法的缺点是：对协态变量初值非常敏感，其收敛域非常狭窄，一般很难直接得到收敛解，尤其对转移轨道飞行时间长、发动机要多次开关切换的情况。

对间接法初值敏感问题，伪谱方法与同伦法有强互补特性。首先，伪谱法可有效求解能量最优时的轨迹和估计协态，其次同伦法可有效求解燃料最优问题(由Bang-Bang控制不光滑性引起)[10-11]。

构建同伦的方式通过对指标添加一个二次摄动项

(31)

此处，增加了一个正乘子λ0以便后续进行归一化。参数ε将燃料最优准则与能量最优准则关联，系数Fmax/(Ispg0)是为当时与实际燃料消耗一致。

根据新的指标，哈密尔顿函数为

(32)

控制力大小为

(33)

式中：ε为同伦算法的参数；ρ为选定的参数，其开关函数形式为

(34)

3 仿真

3.1 从原点至(0，4，0) km点

a)初始轨道选取

假设从星从原点出发到达(0，4，0) km点处，在伪谱同伦法优化前，需选取初始轨道。本文选取的初始轨道是在无任何推力时，从星将根据HCW方程离开原点。如图3所示。

图3 无推力时轨道转移Fig.3 Orbit transfer without thrust

b)伪谱法优化

因z平面内无转移，故只需研究x-y平面内状况。由图3可知：轨道离目标点(0，4) km点越来越远。故将这条初始轨道进行伪谱法修正，从而得到转移轨道和控制曲线分别如图4、5所示)。

图4 伪谱法优化的轨道转移Fig.4 Transfer orbit under optimization ofpseudo spectral method

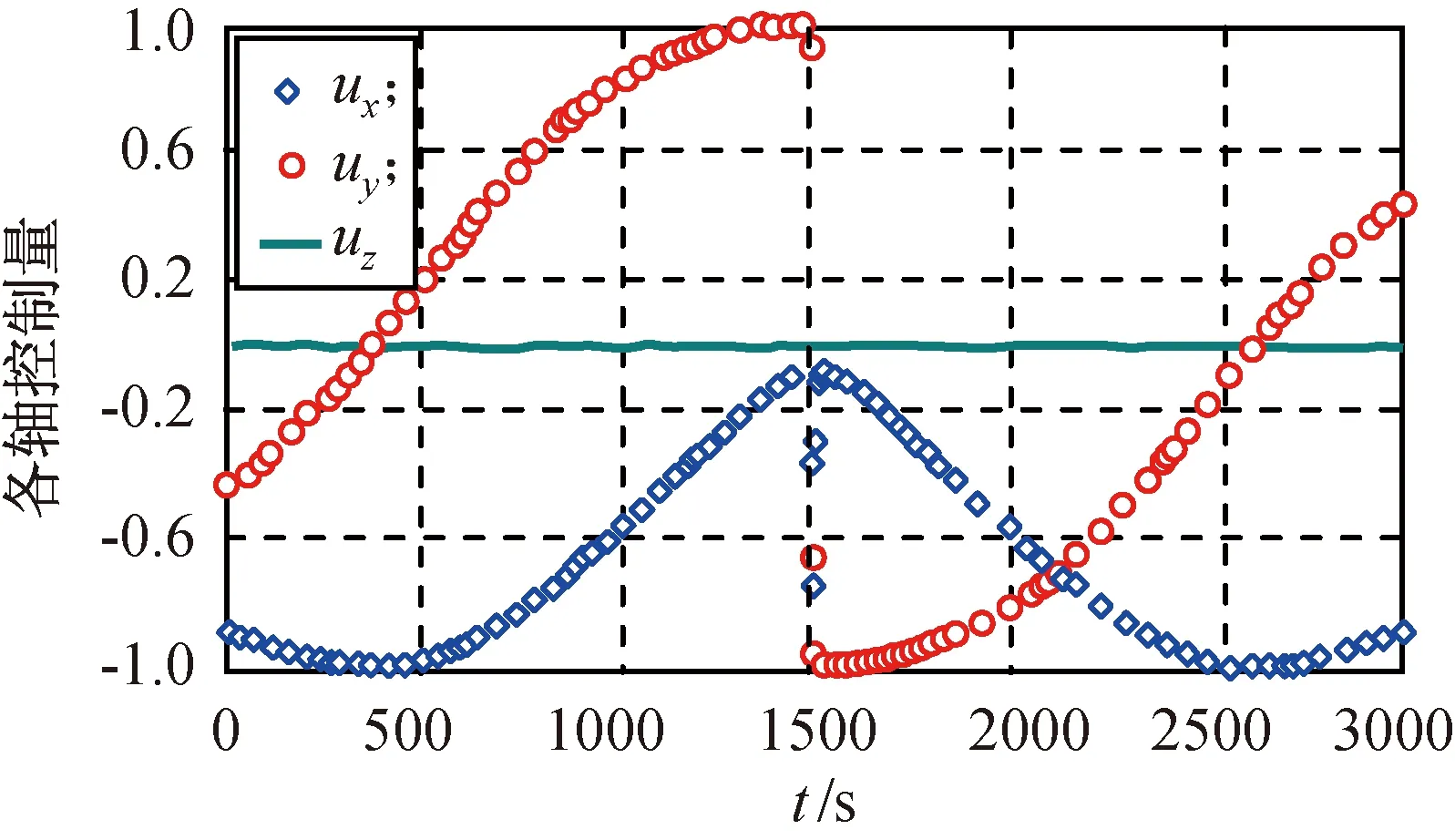
图5 伪谱法优化的各轴控制量Fig.5 Control of each axis under pseudo spectral method

由图4可知：从星从原点飞到目标点(0，4) km，完成了任务。图5对应的是x、y、z三轴上的控制量，可发现因z平面无转移，故一直都是0，而x、y轴也随之变化。

c)同伦法优化

将伪谱法优化得到的轨道再次作为初始轨道进行同伦优化，所得转移轨道、各轴力大小及总力分别如图6～8所示。

图6 同伦法优化的转移轨道Fig.6 Transfer orbit under optimization ofhomotopy method

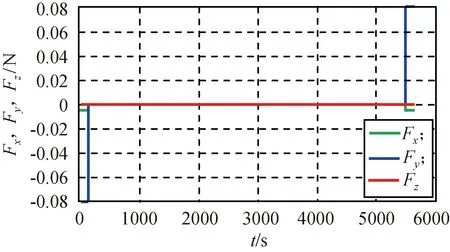
图7 同伦法优化各轴力大小Fig.7 Size of axial force under optimization ofhomotopy method

图8 同伦法优化的总力

图6是由同伦算法得到的轨道。虽然与伪谱法的轨道相近，但仍有较大区别，如图9所示。

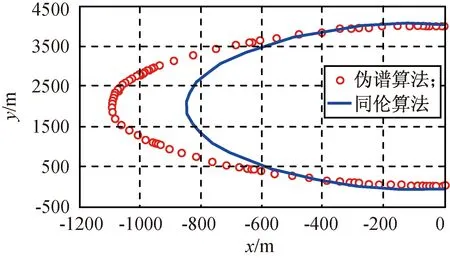
图9 伪谱和同伦优化的轨道Fig.9 Result by pseudo spectrum and homotopy optimization

由伪谱法和同伦法算得的轨道转移时间与燃料消耗见表2。

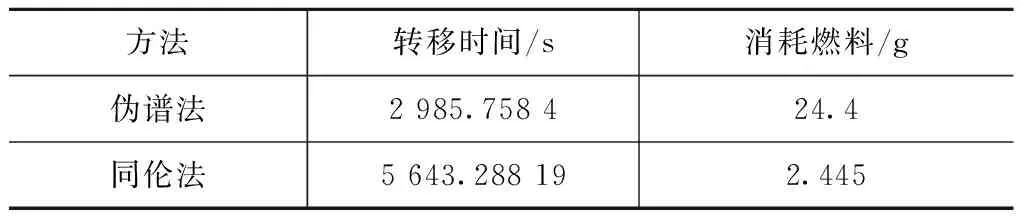
表2 伪谱轨道和同伦轨道比较(0，4) km

由表2可知：虽然转移时间由较大增加，但燃料消耗减小了十分之一。分析原因有两点：首先伪谱法得到的是最优能量的轨道并不是最省燃料的轨道(因其无法求解出最省燃料轨道)；其次同伦法可解决由Bang-Bang控制产生的不光滑性，从而求得最省燃料轨道。本文方法较好地解决了解编队飞行轨道转移的燃料消耗及转移问题。

3.2 从原点至(0，8，0) km点

伪谱法轨道及控制结果如图10、11所示。经同伦优化得到的轨道转移结果如图12所示。伪谱法与同仑优化法所得轨道比较如图13所示。同仑优化法的各轴力大小和总力分别如图14、15所示。

图10 伪谱法优化的轨道转移Fig.10 Transfer orbit under optimization ofpseudo spectral method

图11 伪谱法优化下的各轴控制量Fig.11 Control of each axis under pseudo spectral method

图12 同伦法优化的转移轨道Fig.12 Transfer orbit under optimization ofhomotopy method

图13 伪谱和同伦优化轨道比较Fig.13 Comparison between pseudo spectrum andhomotopy optimization

图14 同伦法优化的各轴力大小Fig.14 Size of axial force under optimization ofhomotopy method

图15 同伦法优化的总力Fig.15 Total force under optimization of homotopy method

伪谱法和同伦法算得的轨道转移时间和燃料消耗见表3。

表3 伪谱轨道和同伦轨道对比(0,8) km

由表3可知：使用同伦法后，消耗的燃料同样明显减少，转移时间也加长。比较表2、3可知：转移距离越长，用伪谱同伦法可节省的燃料越多，且较单独使用伪谱法可节省大量燃料；采用伪谱同伦法到达(0，8) km点消耗的燃料正好是(0，4) km点的2倍。

3.3 从原点至(0，-4，0) km点

求解原点至(0，-4，0) km点的伪谱法轨道及控制结果如图16、17所示。经同伦优化得到的轨道转移结果如图18所示。同仑优化法的各轴力大小和总力分别如图19、20所示。

图16 伪谱法优化的轨道转移Fig.16 Transfer orbit under optimization ofpseudo spectral method

图17 伪谱法优化的各轴控制量Fig.17 Control of each axis under pseudo spectral method

图18 同伦法优化的转移轨道Fig.18 Transfer orbit under optimization ofhomotopy method

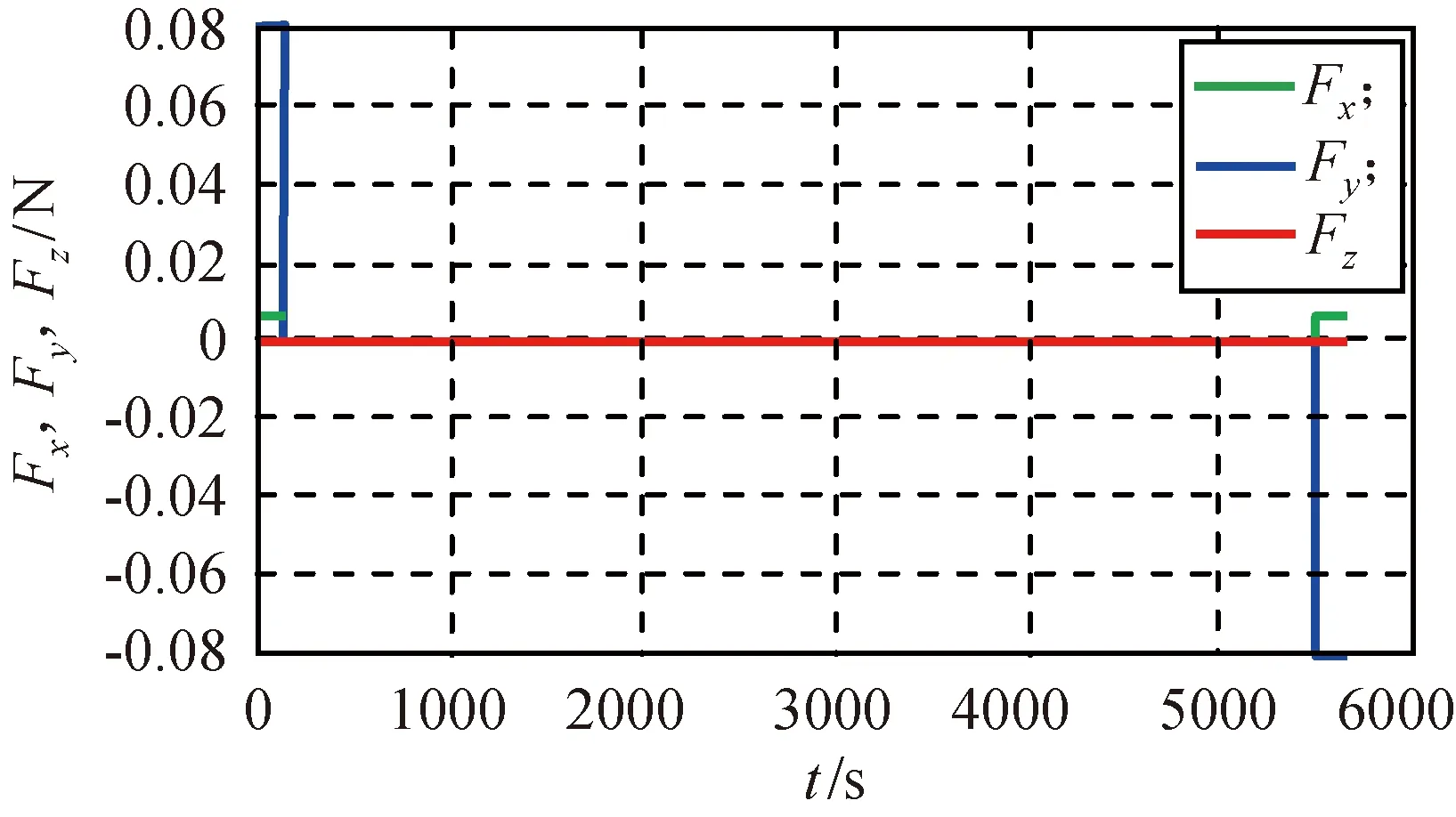
图19 同伦法优化的各轴力大小Fig.19 Size of axial force under optimization ofhomotopy method

图20 同伦法优化的总力Fig.20 Total force under optimization ofhomotopy method

伪谱法和同伦法算得的轨道转移时间和燃料消耗见表4。

表4 伪谱轨道和同伦轨道对比(0，-4) km

由表4可知：使用同伦法后所消耗的燃料也同样大幅减少，转移时间也加长。比较表2、4可知：两者基本无差别，即原点至(0，-4)km是原点至(0，4)km的逆过程。

3颗从星离开原点，构建同轨道跟飞/领飞构型最省燃料的轨道转移如图21所示。全程最耗燃料的仅4.89 g，远小于单独伪谱法的燃料消耗。

图21 3颗从星轨道转移图Fig.21 Transfer orbits of three following-satellites

4 结束语

本文在前人的基础上，将伪谱同伦算法用于求解编队飞行问题中的多个从星飞行任务设计。伪谱同伦算法计算流程为：首先基于大推力的C-W方程，得到了一条大推力转移初始轨道；其次用伪谱法，以性能最优为优化指标进行优化(因其无法解决Bang-Bang控制的不光滑性，故无法得到最省燃料轨道)，得到了一条平滑的控制曲线和小推力转移轨道；再次基于伪谱法得到的小推力转移轨道为初值再进行同伦算法优化，得到了最省燃料的小推力轨道和控制曲线。用本文方法对求解空间轨道的效果较好，证明了该方法最优解的可行性。本文方法解决了伪谱法无法求得Bang-Bang控制引起的不平滑，从而无法得到最省燃料轨道以及同伦算法对初值敏感的问题。但此法尚有其缺点，两种算法结合后计算的难度变大，时间变长。小推力用于深空探测的较多，未来研究将基于限制性三体问题中平动点的编队飞行设计。

[1] 徐劼. 小卫星编队飞行关键技术及发展趋势分析[J]. 航天电子对抗, 2007, 23(6): 24-29.

[2] 高扬. 电火箭星际航行:技术进展、轨道设计与综合优化[J]. 力学学报, 2011, 43(6): 991-1019.

[3] 张友安， 王丽英， 张刚， 等. 轨迹优化的直接数值解法综述[J]. 海军航空工程学院学报， 2012， 27(5)： 481-486+498.

[4] 孙杰, 张东青, 张红英, 等. 库仑力卫星编队动力学建模及基本稳定条件分析[J]. 上海航天, 2015, 32(5): 15-19.

[5] GAO Y, LI W. Systematic direct approach for optimizing continuous-thrust earth-orbit transfers[J]. Chinese Journal of Aeronautics, 2009, 22(1): 56-69.

[6] ROSS I M, GONG Q, SEKHAVAT P. Low-thrust, high-accuracy trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(4): 921-933.

[7] TREFETHEN L N. Spectral methods in MATLAB[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2000.

[8] JAN S H, SIGAL G, DAVID G. Spectral methods for time-dependent problems[M]. New York: Cambridge University Press, 2007.

[9] 王玉浩. 卫星姿态快速机动稳定控制技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.

[10] 郭铁丁. 深空探测小推力轨迹优化的间接法与伪谱法研究[D]. 北京: 清华大学, 2012.

[11] 李俊峰, 宝音贺西, 蒋方华. 深空探测动力学与控制[M]. 北京: 清华大学出版社, 2014.

Design of Formation Flying Mission Based on Pseudo Spectral Homotopy Algorithm

YUE Xiao-kui1, 2, DUAN Xun1, 2

(1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, Shaanxi, China; 2. National Key Laboratory of Space Flight Dynamics, Northwestern Polytechnical University,Xi’an 710072, Shaanxi, China)

In order to optimize the design of following-satellites flight mission, the pseudo spectrum homotopy algorithm was used to get the most provincial fuel transfer orbit with the low-thrust in this paper. The pseudo spectral method was used to optimize the transfer orbit, which was based on the non-thrust case. The transfer orbit would be used as initial value, which solved the problem of the homotopy algorithm for initial value sensitivity. Then the homotopy algorithm was used to solve the problem of the non-smoothness of the Bang-Bang control, which obtained the minimum-fuel trajectory, and the problem of indirect method for solving the optimal control problem was reduced. The numerical example of exactly the same following 3 satellites was designed, which were working on the near earth circular orbit with a height of 400 km, to construct of orbit and fly/flight configuration of the most provincial fuel trajectory. The results show that the pseudo spectrum homotopy algorithm can greatly save fuel and it is feasible and effective for the design of formation flying for the following satellites.

Formation flying; Orbital transfer; Pseudo spectrum homotopy algorithm; Bang-Bang control; Pseudo spectral method; Homotopy algorithm; Minimum-fuel trajectory; Low-thrust

1006-1630(2016)06-0044-09

2016-07-14；

2016-10-18

国家自然科学基金资助(11172235)

岳晓奎(1970—)，男，教授，博士生导师，主要研究方向为航天动力学与控制。

V412.4

A

10.19328/j.cnki.1006-1630.2016.06.006