隔振器安装位置对卫星载荷隔振性能的影响研究
2016-02-15刘兴天郑京良申军烽
刘兴天,郑京良,申军烽
(上海卫星工程研究所 空间机热一体化技术实验室,上海 201109)
隔振器安装位置对卫星载荷隔振性能的影响研究
刘兴天,郑京良,申军烽
(上海卫星工程研究所 空间机热一体化技术实验室,上海 201109)
研究了隔振器安装位置对星载系统隔振性能的影响。针对敏感载荷隔振系统,将隔振器安装位置位移转为敏感载荷在平动与转动方向上的自由度,建立了系统的动力学方程,分析了系统的自由响应和受迫响应,自由响应的结果验证了系统的耦合性以及仿真结果的正确性;受迫响应结果表明耦合系统会出现两个自由度的共振峰,也会出现反共振点。针对平动和转动自由度分别定义了力传递率和力矩传递率,并考虑两种典型隔振器安装位置进行分析,求解了对应于安装位置过质心的耦合系统以及安装位置不过质心的非耦合系统的传递率。发现耦合系统的隔振性能在某些频段和转动方向上优于非耦合系统。结论对微振动的工程设计有一定的参考价值。
微振动; 振动控制; 耦合系统; 敏感载荷; 传递率; 两自由度; 振动响应; 受迫振动
0 引言
遥感卫星的观测分辨率是衡量卫星性能的关键指标之一,但受限于光学系统口径等内部因素,分辨率指标的提升异常困难[1-2]。同时,卫星平台扰振源产生的微振动会对相机的成像造成干扰,致使实际拍摄的相片图像模糊、质量下降,甚至严重影响后期图像解译信息的提取等[3]。因此,必须对卫星在轨微振动进行控制,为敏感载荷提供较安静的工作环境。文献[4]对航天器微振动测试、隔离和抑制技术进行了综述,全面总结了国内外航天器振源建模、地面与在轨测试,以及主被动抑制方法。文献[5]则对近年来的卫星微振动控制技术进行了综述。众所周知,使用被动隔振器能对中高频的微振动进行有效控制,对此国内外进行了大量研究。哈勃望远镜对每个飞轮都采用微振动被动隔离,有效衰减了飞轮轴承引起的高频振动,飞轮最恶劣工况下的干扰力由15 N减小到0.11 N[6-7]。Chandra X-ray观测卫星使用切槽弹簧外加黏性阻尼层对飞轮进行有效隔离,该装置设计了用于发射端缓冲的限位机构[8]。詹姆斯·韦伯太空望远镜使用了约束阻尼层对微振动进行控制[9]。在对敏感载荷进行隔振时需综合考虑其质量和惯量以设计解耦度高的隔振系统,即隔振器的安装位置与质心共面。但敏感载荷的质心常偏离形心,有时也由于载荷结构的约束使隔振器很难通过质心形成解耦。此时,需明确隔振器的安装位置对不同隔振方向隔振效果的影响,以评价隔振设计并进行针对性的改进。文献[10]考虑了精密加工机器的隔振不对中问题,提出了残余振动与多自由度振动耦合间的关系。本文用隔振模型进行理论建模,研究了自由振动和受迫激励下的响应与传递率,讨论了隔振器在敏感载荷上不同安装位置对微振动隔离效果的影响,为隔振器布置提供工程指导。
1 隔振模型及理论建模
敏感载荷由被动隔振器支撑以隔离基础传递来的微振动干扰。设敏感载荷由4个三向刚度隔振器对称支撑,隔振器距离敏感载荷质心的距离分别为l1,l2,隔振器支撑面与质心的垂直距离为l3,且每个方向均有刚度阻尼元件,此六自由度隔振模型如图1所示。在敏感载荷的4个支撑点,每个隔振器均具有3个方向的刚度,提供敏感载荷六个自由度方向的振动隔离。不失一般性,将此系统简化为图2所示的平面系统,并假设隔振器的安装点距离敏感载荷质心有一定的距离。
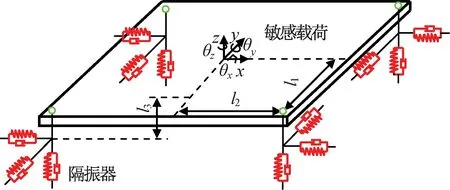
图1 六自由度被动隔振模型Fig.1 Passive vibration isolation system withsix-degree-of-freedom
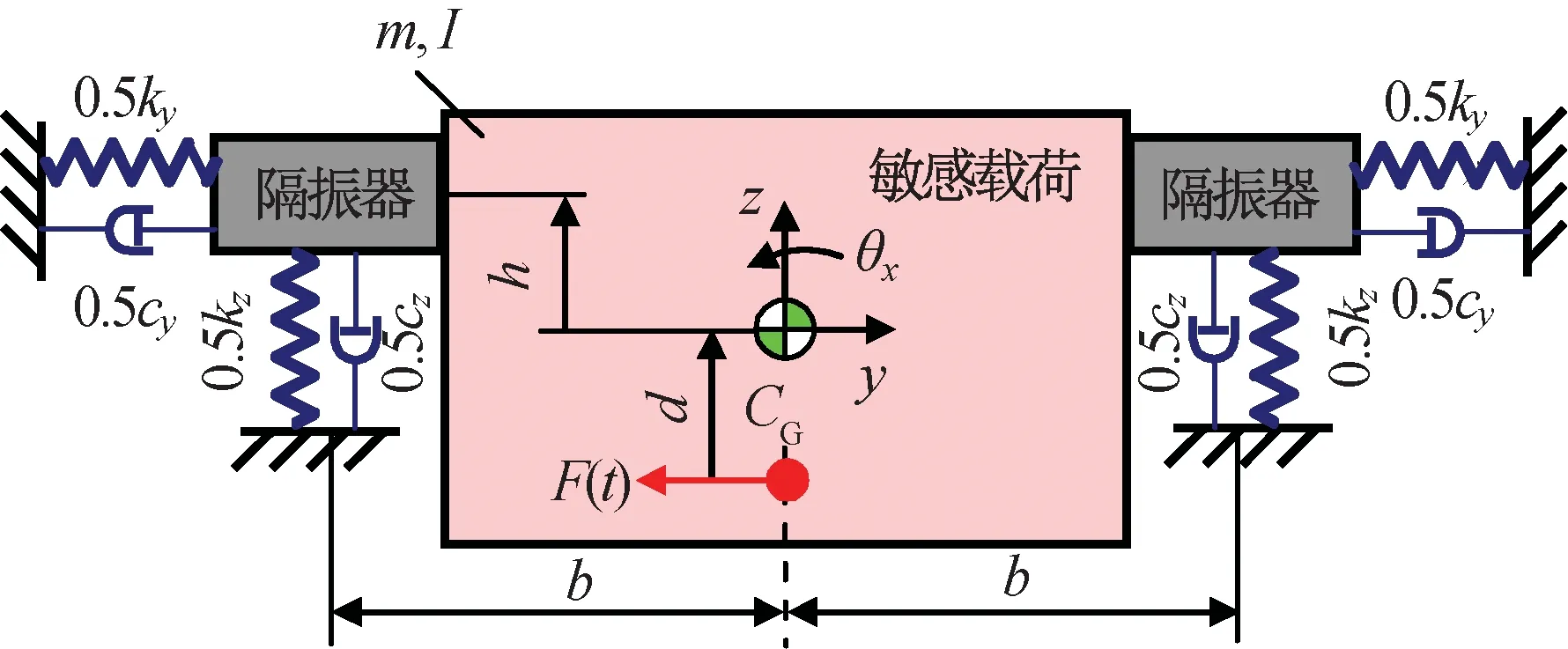
图2 隔振器安装位置不通过质心的平面隔振模型Fig.2 Vibration isolation system in x-y plane
对如图2所示的隔振系统,敏感载荷的质心位于CG处;h为隔振器安装位置与质心的垂直距离;d为敏感载荷激励点与质心的垂直距离;b为隔振器与质心的水平距离;m,I分别为敏感载荷的质量和转动惯量;cy,cz分别为水平阻尼和垂直阻尼。图2中:隔振器由2个具有平面刚度的隔振器支撑,单个隔振器的水平刚度为0.5ky,垂直刚度为0.5kz。系统的动力学方程可表示为

(1)
式中:M,C,K分别为系统的质量阵、阻尼阵和刚度阵,且
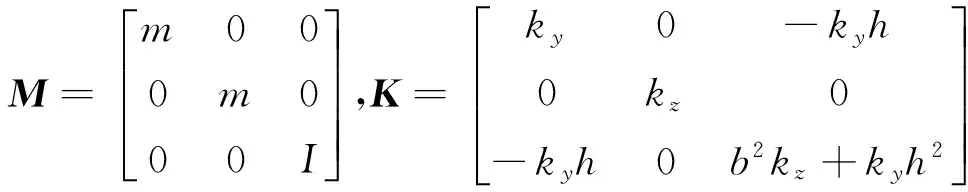

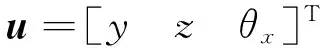
(2)
由式(2)可知:当隔振器安装点不通过质心时,实际上仅y向和θx存在耦合,z向相对较独立。因此,只考虑耦合的自由度,将方程化简为

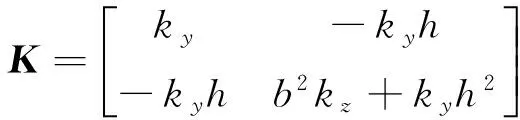
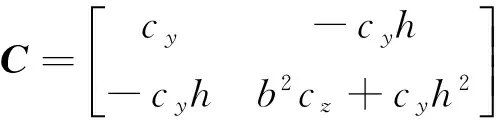
即
(3)
由式(3)可知:两个自由度参数在两个等式中均有出现,说明即使单纯一个方向的运动也会引起另一个方向的运动,两者是耦合的。在式(3)中,令h=0,则此两个自由度解耦,每个方程仅含一个自由度参数,此时隔振器安装位置和敏感载荷质心对其,方程变为
(4)
设被隔振物体受简谐激励F(t)的作用,该简谐激励可能源于卫星上动量轮组件的偏心。则系统受迫振动方程为

(5)
2 自由振动下系统响应
对图2所示的面内隔振动力学模型,隔振器的安装位置分为通过质心和不通过质心两种,这两种安装位置的分析具有代表性。
首先研究隔振系统自由振动下的响应,以分析耦合和非耦合的系统特性。对式(3)、(4)进行响应求解。某敏感载荷的隔振系统参数为:m=130.0 kg;I=20.1 kg·m2;b=0.342 m;h=0.055 m;cy=50 N·s/m;cz=50 N·s/m;ky=5.3×105N/m;kz=6.4×105N/m。因系统存在两个自由度,假设系统的两种初始条件分别为:
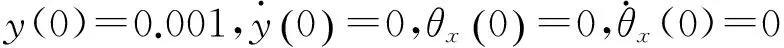
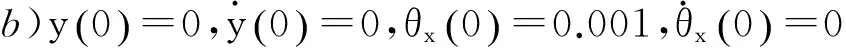
初始条件a)下,仿真所得无耦合和有耦合时系统的振动响应如图3所示。初始条件b)下,仿真所得无耦合和有耦合系统的振动响应如图4所示。由图3、4可知:无耦合状态下,初始条件a)即平动方向的位移仅能引起平动方向的响应,而转动自由度方向的响应为零;耦合状态下,初始条件a)不仅引起了平动方向的自由度,而且即使转动方向无激励,也会引起转动方向的响应,初始条件b)也可得到类似的结论。因为非耦合状态下系统存在理论解,此理论解和此次数值仿真结果经过验证,可推得数值仿真结果的可信性。
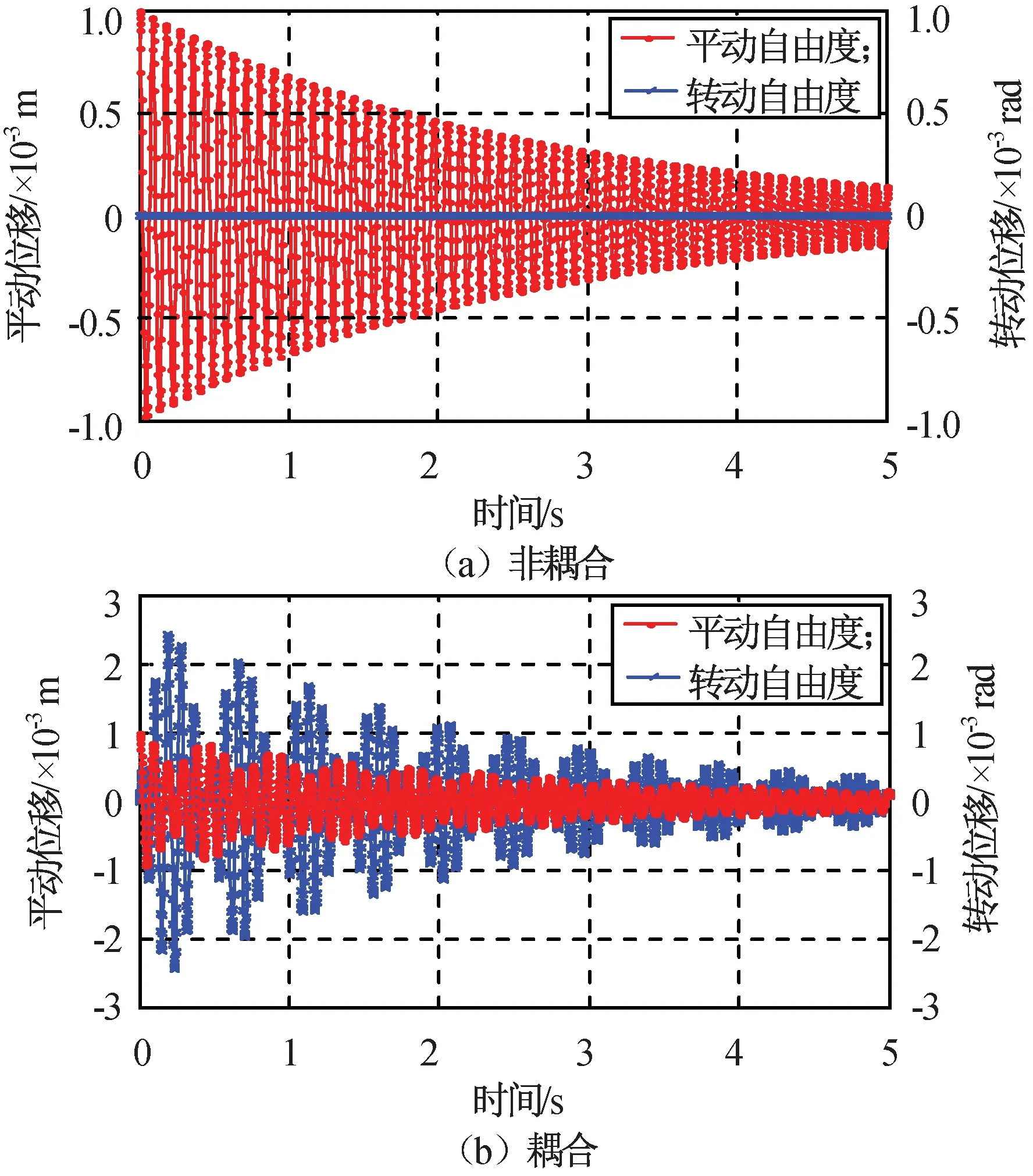
图3 初始条件a)下系统自由振动Fig.3 Free vibration of coupling and non-couplingsystem under initial condition a)
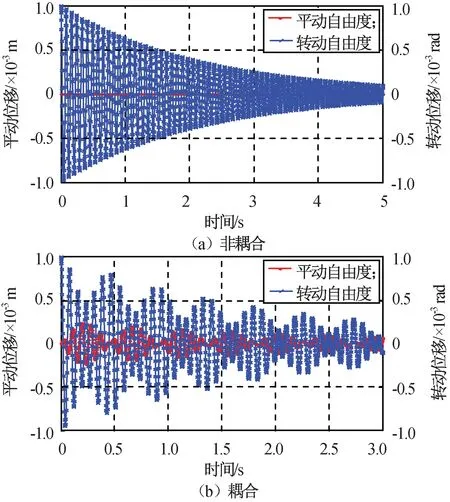
图4 初始条件b)下系统自由振动Fig.4 Free vibration of coupling and non-couplingsystem under initial condition b)
3 受迫激励下系统响应和传递率
设系统的激励力为F0=10N和M0=10N·m。在此组合激励下,耦合系统和非耦合系统均会产生平动与转动向的运动,系统的响应如图5所示。由图5可知:与非耦合系统相比,耦合系统在平动或转动的响应出现峰值2个,这是因为力激励和力矩激励均可在平动和转动方向上产生响应。耦合系统有共振峰2个,同时也有反共振峰1个,这是区别于非耦合系统的重要特征。
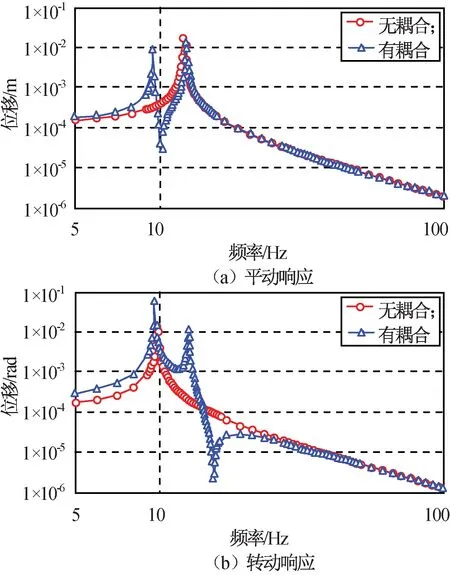
图5 耦合和非耦合时系统响应Fig.5 Translational and rotational response ofcoupling and non-coupling system
隔振系统性能的优劣常用传递率表示。对耦合系统,分别定义力激励下的力传递率和力矩激励下的力矩传递率,传递率的表达式为

(6)
式中:At为传递至基础的力或力矩;A0为激励力或激励力矩的幅值。系统的传递率如图6所示。由图6可知:与非耦合系统相比,耦合系统的力传递率在低频出现峰值1个,这是由转动方向引起的。除引起的峰值外,耦合系统的力传递率在高频时与非耦合系统基本一致;力矩传递率表明耦合系统的高频衰减效果更好。
由图5、6可知:耦合系统传递率的最低点并不一定对应响应的反共振点,这是因为系统传递至基础的力或力矩的方向可能发生改变,在方向发生改变时存在最低点。
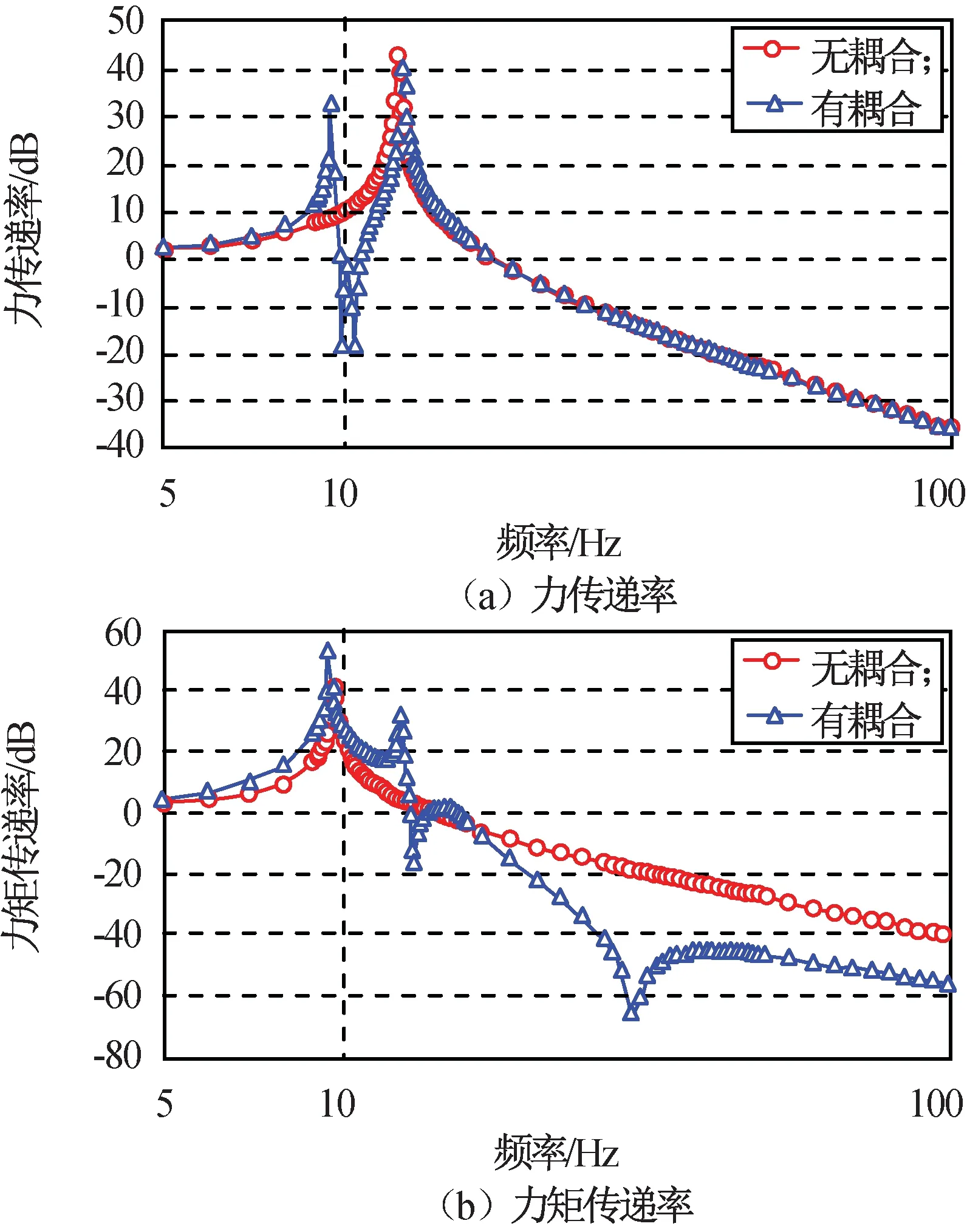
图6 耦合和非耦合时系统的力传递率和力矩传递率Fig.6 Force and moment transmissibility ofcoupling and non-coupling system
考虑在轨运行时,系统对转动方向的微振动抑制需求更强烈,耦合系统的隔振效果并不一定劣于非耦合系统。就高频转动隔振而言,耦合系统的隔振性能甚至优于非耦合系统。
4 结束语
本文研究了对敏感载荷进行被动隔振时隔振器布置位置对隔振性能的影响。对耦合和非耦合隔振系统进行了理论建模,用数值方法求解了系统的自由振动响应,说明了系统存在耦合时系统的响应特性。定义了系统的力传递率和力矩传递率,分析了隔振器不同安装位置下系统的传递率。研究表明:若感兴趣的振动控制集中于某一方向,则非耦合系统的隔振性能会优于耦合系统,不必要必须进行隔振器的解耦安装设计。此结果对实际的工程应用提供更宽的指导思想。相对于目前普遍的工程应用,本文创新性地提出隔振器在某些情况下没必要进行解耦设计,但是本研究结果处于理论和仿真阶段,尚未进行试验验证,后续需进行试验验证,验证后可通过隔振器的耦合设计,提高关心方向的隔振效果。
[1] 孙阳. 卫星平台在轨颤振对高分辨率遥感器成像质量影响的研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2013.
[2] 董瑶海. 航天器微振动——理论与实践[M]. 北京: 中国宇航出版社, 2015.
[3] 赵光旭. 相机平台颤振对高分辨率光学遥感成像的影响分析[D]. 成都: 西南交通大学, 2015.
[4] 谭天乐, 朱春艳, 朱东方, 等. 航天器微振动测试、隔离、抑制技术综述[J]. 上海航天, 2014, 31(6): 36-45+51.
[5] 孟光, 周徐斌. 卫星微振动及控制技术进展[J]. 航空学报, 2015, 36(8): 2609-2619.
[6] DAVIS L P, WILSON J F. Hubble space telescope reaction wheel assembly vibration isolation system: Structural dynamics and control interaction of flexible structures[R]. NASA, N87-22702, 1986.
[7] WILSON G. W, WOLKE P J. Performance prediction of D-strut isolation systems: Passive Damping and Isolation Conference, Proceedings of SPIE[C]// San Diego: The International Society for Optical Engineering, 1997.
[8] PENDERGAST K J, SCHAUWECKER C J. Use of a passive reaction wheel jitter isolation system to meet the advanced X-ray astrophysics facility imaging performance requirements[C]// Space Telescopes and Instruments V, Proceedings of SPIE. Kona: The International Society for Optical Engineering, 1998: Part 2 (A99-10753) 01-19.
[9] BRONOWICKI A J. Vibration Isolator for large space telescopes[J]. Journal of Spacecraft & Rockets, 2006, 43(1): 45-53.
[10] OKWUDIRE C E, LEE J. Minimization of the residual vibrations of ultra-precision manufacturing machines via optimal placement of vibration isolators[J]. Precision Engineering, 2013, 37(2): 425-432.
Effect of Installation Position of Isolators on Micro-Vibration Isolation Performance for Satellite Payload
LIU Xing-tian, ZHENG Jing-liang, SHEN Jun-feng
(Laboratory of Space Mechanical and Thermal Integrative Technology, Shanghai Institute of Satellite Engineering, Shanghai 201109, China)
The effect of installation position on the performance of vibration isolation system on borne was analyzed. Considering the vibration isolation system of sensitive payload, the isolation position of the isolator was transfered into translational and rotational degree of the payload. The dynamic equation of the system was established. The free and forced vibration responses of the system were analyzed. The result of free response has verified the existence of coupling in the system and the accuracy of the simulation result. Meanwhile, the result of forced response shows that the frequency resonance change from one to two accompanied with one anti-resonance point. For translational and rotational degree of freedom, the force transmissibility and moment transmissibility were defined. The two typical installation positions of the isolator were analyzed. The transmissibility was analyzed for both coupling and non-coupling systems respectively. It is found that the performance of the coupling system can be superior to the non-coupling system for different frequency range and isolation direction. The result can provide meaningful instruction to design micro-vibration isolation system in engineering.
Micro-vibration; Vibration control; Coupling system; Sensitive payload; Transmissibility; Two degree of freedom; Vibration response; Forced response
1006-1630(2016)06-0067-05
2016-05-31;
2016-07-30
国家自然科学基金资助(51505294);上海市科委资助(14XD1423000)
刘兴天(1984—),男,博士,主要研究方向为非线性动力学、结构振动控制。
V414.5
A
10.19328/j.cnki.1006-1630.2016.06.009
