固定资产定积分折旧建模思路新探——折旧的中间年限加速计提猜想

郑智勇

（福建师范大学经济学院，福建福州350108）

固定资产定积分折旧建模思路新探
——折旧的中间年限加速计提猜想

郑智勇

（福建师范大学经济学院，福建福州350108）

在现行的资产负债观的视角下，对于原值实现价值的全部补偿是不符合当今对于资产内部损耗的合理估计，从总体上看，固定资产的折旧额随着固定资产的价值损耗呈现出先上升后下降的趋势，为了使得所计提的折旧额能够较合理地反映资产的实际损耗，本文引入了定积分的折旧思路，根据资产的不同特点，选择相应的折旧模型，并进行合理的折旧估计，更好地保证折旧计提的可靠性和客观性。

资产负债观；定积分；二次函数；正态分布；三角函数

当前固定资产的折旧方法主要是年限平均法、工作量法、余额递减法、双倍余额递减法和年数总和法这五种方法。然而现行的这五种折旧方法主要考虑从折旧基数和折旧率的变化情况来探讨各期折旧额的内在规律性，通过原值、净残值和折旧年数来计提各期的折旧额，而忽视了各资产的价值损耗特点。显然在现行的资产负债观的视角下，对于原值实现价值的全部补偿是不符合当今对于资产内部损耗的合理估计，而只有充分从资产自身的特点来考虑折旧计提的合理性，才能更好地实现会计“估价人”的角色，折旧的计提才更具有可靠性和客观性。因此引入了定积分的折旧思路，根据资产的不同特点，选择相应的折旧模型，并进行合理的折旧估计，使得所计提的折旧额能够较合理地反映资产的实际损耗。对于定积分的折旧思路主要从一元积分和二元积分的角度来研究固定资产的折旧，通过反映其折旧规律的二次函数、正态分布函数、三角函数等函数图像以及椭圆等折旧图形，按照其在各资产特点进行相应的变动，从而合理估计出其折旧额的变动。本文认为固定资产的折旧趋势是呈现中间年限的加速化趋势的，在固定资产使用初期，由于不能很好地掌握固定资产的操作技术，有效地管理固定资产的能耗，因此初期的折旧额处于较低的水平，随着时间的延长，操作技术的提高，为了能最大限度地创造出固定资产的使用价值，固定资产的价值损耗就会随着操作效率的提高而逐渐增大，折旧额也会因此呈现出递增的趋势，当固定资产的使用效能达到最大值后，随着固定资产损耗的增加，固定资产的修理费用的增多，固定资产的性能减弱，折旧额在达到最高点后逐渐下降。所以从总体上看，固定资产的折旧额随着固定资产的价值损耗呈现出先上升后下降的趋势，因此通过新模型的构建来实现该趋势的折旧计提，实现折旧计提的最优化。

对于折旧新方法的探索上，考虑到折旧的中间年限加速计提，当前研究主要集中于对正态分布折旧法的探索，却没有从积分的角度来研究固定资产的折旧新方法。孙芳城等探索用二分法来改进原有折旧[1]。刘兴革等根据正态分布的特点，提出正态分布法的折旧计提[2]。代宏霞等出于折旧额的内在价值真正弥补固定资产内在价值的考虑[3],章新蓉从资金运动的增值现象出发将资金时间价值引入以优化固定资产正态折旧模型[4]。林祥友认为虽然固定资产正态折旧模型使得各期的折旧额绝对数的分布具有正态合理性，但是存在着折旧总额误差大和各期折旧额相差大的缺陷，并在此基础上提出动态模型的修正思路：可以通过同时除以总折旧区间单位以确保折旧率之和等于1，或者引入权数直接调整各期折旧率[5]。陶英恒等从不确定性的角度分析了固定资产年利率的不合理性，提出用区间来表示年利率，建立了基于区间数的固定资产动态正态折旧模型，并且结合实例证明了该模型的合理性[6]。

1 定积分折旧的模型构建

1.1 一元定积分折旧模型

原理：设f（x）在区间[a,b]上连续且f（x）≥0，以曲线y=f（x）为曲边，底为[a,b]的曲边梯形的面积A表示为

1.1.1 二次函数折旧法

分析思路：二次函数折旧法是利用a<0,=0,c>0的二次函数在第一、二象限与X轴、Y轴围成的面积作为固定资产的原始价值，在该函数与X轴的两个交点这一区间内按折旧年限平均划分，各年的折旧率即为相应折旧年限区间作垂线与该二次函数曲线所围成的面积元与总面积的比例（如图1）。

设购买某固定资产的原始价值为P，预计使用年限n年，Dn为各期的折旧额；设折旧的曲线方程为y=ax2+c（a<0,c>0）。计提步骤：

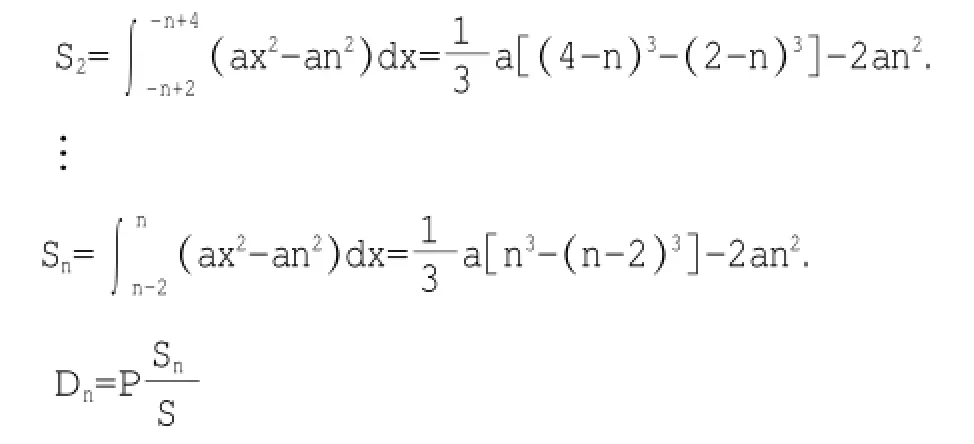
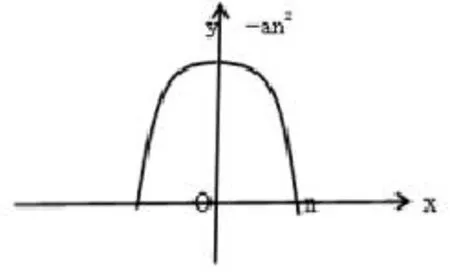
图1 二次函数折旧法函数图像Figure 1 Quadratic function method of depreciation function image

1.1.2 正态分布折旧法

分析思路：正态分布折旧法是通过正态分布的概率密度函数曲线向两端无穷延伸，在（u-3σ，u+3σ）区间与X轴所围成的曲边梯形的面积为1来考虑的，因此选择标准正态分布函数，把（-3,3）与X轴围成的曲边梯形的面积看作1，按照折旧年限对（-3,3）进行合理划分区间，并对每一区间积分来确定折旧率。

设购买某固定资产的原始价值为P，预计使用年限n年，即在（-3,3）区间上平均分成n份，每份长度为，Dn为各期的折旧额。计提步骤：

1.1.3 三角函数折旧法

设购买某固定资产的原始价值为P，预计使用年限n年，Dn为各期的折旧额。计提步骤：

1.2 二元定积分折旧模型

原理：设f（x，y）在小闭区域Δσi上连续且f（x，y）≥0，以函数y=f（x，y）为底面的曲顶柱体的体积V表示

分析思路：二元定积分折旧模型是利用椭圆的结构特点，在椭圆的长轴上平均划分折旧年限，在每个折旧年限区间内计算各区间内截得的椭圆面积，并除以椭圆的总面积以估计出当期的折旧率，所以从椭圆面积的整体变化上看，折旧率呈现出正态变化的特点。

设购买某固定资产的原始价值为P，预计使用年限n年，Dn为各期的折旧额。计提步骤：

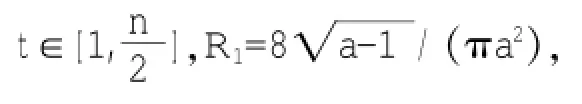
2 数据检验

当折旧年限为6年，净残值为0时，按以上四种方法计提的折旧率如表1和图2：

表1 四种折旧方法的折旧率计提Table 1 Four kinds of method of depreciation allowance for depreciation provisions

图2 四种折旧新方法的折旧率变化趋势图Figure 2 Four new methods of depreciation allowance for depreciation trend image

3 模型分析

从图2上分析可知，这四种折旧方法都呈现出凸型对称的折旧趋势变化，即呈现出初期和末期折旧计提少，中期折旧计提多的中间年限加速计提趋势。其中正态分布折旧法折旧率的变化趋势最为陡峭，变化幅度在30%左右，椭圆折旧法的变化趋势最为平缓，变化幅度在10%以内，二次函数折旧法和三角函数折旧变化趋势适中，变化幅度在20%左右，并且两者的变化趋势能够基本上相互拟合。初期和末期的正态分布折旧法、二次函数折旧法和三角函数折旧法的折旧率都在10%以内，椭圆折旧法的折旧率则超过了10%，二次函数折旧法、三角函数折旧法和椭圆折旧法的折旧率的极值都在20%～30%之间，而正态分布折旧法的极值则超过了30%。这些差别是由于折旧图形的自身形状的差异决定的，正态函数图像到峰值的切线斜率总体上不断增大的，由于其图像是向原点处内凹的，所以其递增的趋势是加速的。椭圆图形则是明显向外凸的，这意味着其切线斜率总体上不断减小的，而且其递减的趋势是减速的。二次函数和三角函数图像的折旧区域形状比较类似，所以其折旧计提得较为拟合，这两个函数的图像也是向外凸的，这意味着其切线斜率总体上不断减小的，而且其递减的趋势是减速的，但是减速趋势相对椭圆来说要减缓得多。综上可知，正态分布折旧法更适用于难操作，且操作中期随着技术操作的熟练产生大量能耗的固定资产，椭圆折旧法更适用于易操作，且操作中期随着技术操作的熟练产生少量能耗的固定资产，二次函数折旧法和正态分布折旧法则更适用于居中的情形。

4 研究结论

在现行的资产负债观的视角下，会计越来越成为一种“估价人”的角色，由于固定资产的折旧额与税收缴纳、现金流的估计都是息息相关的，如何更加合理地估计固定资产在折旧年限内的价值损耗，从真正意义上客观准确地计量出固定资产的非付现成本成为当前值得研究的一个方向。本文认为固定资产的加速折旧法不能合理地反映固定资产的内在损耗情况，而固定资产实际的价值损耗应该是呈现中间年限的加速化趋势的，因此探讨了四种中间年限加速计提折旧的折旧方法，并分析了四种折旧方法各自的特点，然而这四种折旧方法的缺陷也是显而易见的：计提的折旧数呈现对称分布的，意味着这四种折旧方法的使用是假设期初和期末各期计提的折旧数是完全一致的，这显然也是与当前资产的实际损耗不一致的；这四种折旧方法在使用时，没有准确地考虑到资产自身的特点，包括磨损程度、腐蚀程度或更新换代速度等因素，而笼统进行折旧率的估计，导致估计具有很大的片面性。所以进一步保证折旧估计的合理性还需要从这两个方面进行完善，才能够实现折旧计提的最优化。

[1]孙芳城，郭华.固定资产折旧方法新探[J].财会月刊，2005(9): 41-42.

[2]刘兴革，黄彦涛，刘利君.关于运用正态分布法计提固定资产折旧的探讨[J].商业研究，2004(11):42-44.

[3]代宏霞，蓝文永，林祥友.固定资产正态动态折旧模型的构建[J].企业天地，2007(9):152-153.

[4]杨璐，章新蓉，王琴.建立动态的正态分布固定资产折旧模型[J].财会月刊，2008(3):28-29.

[5]林祥友.固定资产正态折旧模型的构建与修正[J].财会月刊，2008(8):73-74.

[6]陶英恒，李勇，兰继斌.固定资产区间动态正态折旧模型研究[J].财会月刊，2008(9):48-49.

[7]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京：高等教育出版社，2010:46-50.

[8]杨德芳.固定资产折旧年限确定的帕累托最优[J].嘉兴学院学报，2006(6):70-73.

[9]乔计兵.关于企业固定资产折旧方法的探讨[J].经济师，2013(5):117-118.

[10]葛柳燕.利用excel测算固定资产折旧的新方法[J].财会月刊，2013(2):109-110.

（责任编辑：华伟平）

Fixed Assets Depreciation New Modeling Approach of Definite Integral——In the Middle of the Fixed Number of Year Accelerated Depreciation Provision

ZHENG Zhiyong
(School of Economics,Fujian Normal University,Fuzhou,Fujian 350108)

Under the view of the current assets and liabilities,the original value realizing the value of all the compensation is not up to reasonably estimate internal loss of assets today,overall,fixed assets depreciation of fixed assets with the loss of value show a downward trend after rising first,in order to make the provision of depreciation reflect the actual loss of assets more reasonably,this article introduced the depreciation method of definite integral,according to the different characteristics of assets,choosing corresponding depreciation model,and carring on the reasonable depreciation estimate guarantee the reliability and objectivity of the depreciation provision better.

assets and liabilities’view;definite integral;quadratic function;normal distribution;trigonometric functions

F-275

A

1674-2109（2016）12-0066-05

2016-07-16

郑智勇（1992-），男，汉族，在读研究生，主要从事财务会计理论研究。