ELMD与排列熵在滚动轴承故障诊断中的应用*

李伟娟，陈 帅，张 超

(1.包头职业技术学院，内蒙古 包头 014030； 2. 内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

ELMD与排列熵在滚动轴承故障诊断中的应用*

李伟娟1，陈 帅2，张 超2

(1.包头职业技术学院，内蒙古 包头 014030； 2. 内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

针对轴承故障信号往往被强背景噪声淹没，采用传统包络解调方法难以提取故障特征的问题，提出总体局部均值分解(ensemble local mean decomposition, ELMD)与排列熵(permutation entropy, PE)相结合的轴承故障诊断方法。首先，对轴承振动信号进行ELMD分解并得到一系列窄带乘积函数(product function, PF)，然后，计算各PF分量排列熵以构造高维特征向量，最后将高维特征向量作为多故障分类器的输入来识别轴承故障类型。实验结果表明ELMD方法可以有效地抑制模态混叠；PF分量的排列熵分布可以反应轴承不同工作状态下的信号特征；基于ELMD与排列熵的智能诊断方法可以准确地识别轴承的工作状态和故障类型。

排列熵；总体局部均值分解；高维特征向量；模态混叠；故障诊断

0 引言

轴承是旋转机械中最易损坏的机械零部件之一，很多机械故障都和轴承工作状态密切相关。因此，能否快速、精准、容易地检测出轴承故障的存在和严重程度对于保持轴承安全可靠地运行和减少设备停机成本意义重大[1]。由于加载，摩擦，刚度的影响，轴承故障振动信号往往呈现非线性和非平稳性，而传统的时域或频域分析方法都是基于线性、稳态系统，不能有效地检测出故障信号的动力学突变，因此难以精确、稳定地识别轴承的故障类型[2]。

局部均值分解(local mean decomposition，LMD)[3-4]是一种自适应时频分析方法，特别适合于非线性非平稳信号的处理，但是LMD和经验模态分解(empirical mode decomposition，EMD)[5-7]一样，都存在严重的模态混叠，模态混叠可能会使分解得到的PF分量失去物理意义。为了抑制模态混叠，杨宇和程军圣提出了总体局部均值分解(ensemble local mean decomposition, ELMD)方法[8]。通过不断的在原始信号中加入高斯白噪声，改变原始信号极值点的分布，从而一定程度上抑制模态混叠。

最近，Yan[9]等将排列熵(permutation entropy, PE)引入旋转机械故障诊断领域，其通过对比相邻数据去度量时间序列的复杂性。与其他熵值相比，排列熵具有计算简单、抗噪能力强、适合在线监测等优点[10]。据此，提出将ELMD与排列熵相集合，对轴承信号进行ELMD分解，计算各PF分量的排列熵，构造高维特征向量作为最小二乘支持向量机(least squares support vector machine, LS-SVM)的输入来识别轴承故障类型。

1 ELMD算法

1.1 ELMD算法

ELMD方法是基于LMD方法的模态混叠问题而提出，由于白噪声信号具有频率均匀分布的统计特性，通过不断的在原始信号中加入高斯白噪声，可以改变原始信号极值点的分布，从而抑制模态混叠。但是添加的白噪声也会掺杂到LMD分解得到的PF分量中，使PF分量失去物理意义。考虑到数量足够多的白噪声其均值为0，通过对目标信号多次添加白噪声可以抵消白噪声的干扰。ELMD分解具体的步骤如下[8]：

(1) 初始化高斯白噪声的加入次数M。

(2) 添加幅值为常数的高斯白噪声到原始信号y(t)中生成新的混合信号：

yi(t)=y(t)+ni(t)

(1)

这里ni(t)表示第i次添加的白噪声序列，i=1, 2, …,M。

(3) 使用LMD方法分解新产生的混合信号yi(t)，生成一系列的PF分量。

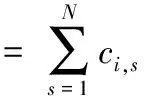
(2)

(4) 重复步骤(2)、(3)M次，每次添加不同的白噪声序列，获得一个PFs的集合：

(3)

式中，s=1，2，…N。

(5) 计算分解得到的相应PFs分量的总体平均作为最终的分解结果：

(4)

式中，cs(t)是通过ELMD分解得到的第s个PF分量，j=1,2,…,M；s=1，2，…，N。

1.2 仿真信号分析

为了验证ELMD方法能有效地抑制模态混叠，构造如下的仿真信号：

(5)

式中：τ=6×10-7s,t0=0.005s,t1=0.015s,0≤t≤0.025，仿真信号及其各成分组成如图1所示。

图1 仿真信号及其各组成成份的时域波形图

对仿真信号进行LMD分解，分解得到3个PF分量和一个残余分量u，其时域波形图如图2所示，从图2可以看出各PF与原始信号差异较大，模态混叠严重。

图2 仿真信号LMD分解结果

固定白噪声等级为0.1，总体平均次数为100，ELMD分解结果如图3所示，从PF1分量中可以看出明显的冲击成分，与实际分量x1(t)非常接近，余下的各PF分量是低频部分，也接近于实际分量x2(t),x3(t)，故ELMD方法可以较好的将冲击成分和低频成分分开，从而有效地抑制了模态混叠。

图3 仿真信号ELMD分解结果

2 排列熵

排列熵是通过对比相邻数据的大小，来检测时间序列的动力学突变，而数据的具体值不参与运算，从而可以有效地避免噪声的干扰和降低计算的复杂性。其基本原理如下[11]：

对于任意给定的时间序列{x(k),k=1, 2, …,N},根据嵌入定理，在时刻i处的D维延迟嵌入向量定义为:

(6)

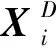
(1) x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤…≤x(i+(jD-1)τ)

(2) 如果x(i+(js-1-1)τ)=x(i+(js-1)τ)，则js-1

每类πj符号序列的概率计算如下：

(7)

(8)

显然0≤HP(D)≤ln(D!)，因为对于一个单调序列HP(D)=0，而对于一个完全随机的序列，由于每种符号序列出现的概率都是1/ln(D!)，故HP(D)=ln(D!)。为了便于统计分析，将公式(8)进行归一化处理即：

(9)

由定义可知，排列熵可以反应时间序列的局部特征：Hp(D)越小，时间序列就越规则，Hp(D)越大，时间序列就越不规则，或随机性越大。因此排列熵可以作为度量时间序列的复杂性和检测动力学突变的指标。

3 基于ELMD与排列熵的轴承故障诊断

当轴承发生故障时，会激起故障源的非线性振动，此时轴承振动信号的复杂性会发生变化[12]。虽然排列熵可以用来度量信号的复杂性，但是仅仅使用排列熵并不能识别轴承不同工作状态下的故障。因为来自于实际的轴承振动信号通常是复杂的，由多个振源共同激发。考虑到ELMD方法可以自适应的将振动信号分解为一系列不同时间尺度的的PF分量，因此可以用各PF分量的排列熵来揭示振动信号不同时间尺度的内在特性，从而为故障诊断提供准确的信息。基于ELMD与排列熵的轴承故障诊断流程如图4。

图4 基于ELMD与排列熵的轴承故障诊断流程

其具体实现步骤如下：

(1) 在滚动轴承正常、内圈、外圈和球体故障下，按一定的采样频率fs分别进行k次采样，共获得4k个信号。从每类信号中分别随机抽取m个信号作为训练样本,n个信号作为测试样本(m+n=k)。

(2) 对其中任一信号执行ELMD分解，选取包含主要故障的前6个PF分量；

(3) 确定排列熵的时延系数τ=1和嵌入维数D=6,分别计算前6个PF分量归一化的排列熵，构造高维特征向量:

T=[PE1,PE2,…PE6]

(10)

(4) 重复(2)、(3)步，直至求取4k个信号的高维特征向量。

(5) 建立由3个LS-SVM组成的多故障分类器。LS-SVM1区分有无故障，LS-SVM2区分内圈故障、LS-SVM3区分外圈故障，若以上三种状态都不是，则断定滚动体有故障。然后将训练样本的特征向量T输入LS-SVM进行训练。

(6) 将测试样本的特征向量T输入已经训练好的LS-SVM分类器中，以LS-SVM分类器的输出确定轴承故障类型。若输出的结果为+1，则认为是正常，测试结束；否则输入LS-SVM2，直至LS-SVM3。

建立的滚动轴承故障分类器结构如图5所示。

图5 滚动轴承故障分类器结构

4 应用实例

为了验证本文提出方法的有效性，选用美国凯斯西储大学轴承数据进行试验。测试轴承来自于电机驱动端的6205-2RS深沟球轴承，分别截取12kHz采样频率下的轴承正常、内圈故障、外圈故障、球体故障的数据40组，共计160组数据，每组数据取2400个采样点。各种状态下随机抽取20组数据作为训练样本，剩下的20组数据作为测试样本。

图6是正常状态和不同故障类型下的PF分量排列熵的值，从图中可以看出内圈故障、外圈故障、滚动体故障的PE值都比正常状态下的高，这是因为当轴承发生故障时，由故障引起的高频冲击成分将会出现在振动信号中，通过ELMD分解得到的PF分量的复杂度将会增加，排列熵值也会增大。从图6还可以看出不同工作状态下PF分量的排列熵虽然都有着逐渐减小的变化趋势，但有着不同的分布，因此排列熵的分布情况可以用来反应轴承的工作状态。

图6 正常状态和不同故障类型下的PF分量排列熵值

固定白噪声等级为0.2，总体平均次数为100时，轴承各种状态下的ELMD排列熵特征向量如表1所示。(由于篇幅所限，表中仅列出每种工作状态下5个信号的特征向量)。

表1 不同工作状态下ELMD分解得到的特征向量

LS-SVM测试结果如表2所示，从表2中可以看出基于ELMD与排列熵的滚动轴承故障诊断方法准确率达到100%。表2中还对比了基于ELMD与排列熵和LMD与排列熵的分类器性能，发现ELMD与排列熵分类器准确度更高，更具有良好的推广能力。

表2 不同方法的LS-SVM故障诊断结果

5 结论

针对轴承故障信号特征信息难以提取的问题，本文提出ELMD与排列熵的滚动轴承故障诊断方法。选用LS-SVM作为多故障分类器，将ELMD分解得到的PF分量的排列熵作为分类器的输入识别轴承故障类型和工作状态。通过仿真信号和实际信号分析，得出的结论如下：

(1) ELMD方法可以有效地抑制LMD分解过程中的模态混叠。

(2) ELMD与排列熵的智能诊断方法比同一过程的LMD与排列熵的智能诊断精度高，进而为工程实际信号的故障诊断打下坚实的基础。

[1] Zhang Xiao-yuan, Liang Yi-tao, Zhou Jian-zhong, et al. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM[J]. Measurement,2015,69:164-179.

[2] 任学平，辛向志，庞震，等. 基于IMF熵的多传感器网络融合滚动轴承故障诊断方法研究[J]. 组合机床与自动化加工技术，2015(6)：78-82.

[3] 张超，陈建军. 基于LMD和Lempel-Ziv指标的滚动轴承故障损伤程度研究[J]. 振动与冲击，2012，31(16)：77-82.

[4] 王建国，李健，万旭东. 基于奇异值分解和局域均值分解的滚动轴承故障特征提取方法[J]. 机械工程学报,2015 51(3):104-110.

[5] 籍永建，王红军. 基于EMD的主轴振动信号去噪方法研究[J]. 组合机床与自动化加工技术，2015(5)：35-37.

[6] 郭正才，王义强，朱艳飞，等. 基于EMD-AR谱分析的数控机床主轴故障诊断方法研究[J]. 组合机床与自动化加工技术，2016(3):93-96.

[7] 马文朋，张俊红，马梁，等. 改进的经验模式分解在机械故障诊断中的应用[J]. 振动、测试与诊断，2015, 35(4)：637-644.

[8] YANG Yu, CHENG Jun-sheng, ZHANG Kang. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems[J]. Measurement, 2012, 45(3): 561-570.

[9] Yan Ru-qiang, Liu Yong-bin, Gao X. Permutation entropy: a nonlinear statistical measure for status characterization of rotary machines[J].Mechanical Systems and Signal Processing, 2012, 29(5): 474-484.

[10] 周涛涛，朱显明，彭伟才,等. 基于CEEMD和排列熵的故障数据小波阈值降噪方法[J]. 振动与冲击，2015，34(23): 207-211.

[11] Bandt C，Pompe B. Permutation Entropy: a Natural Complexity Measure for Time Series[J]. Physical Review Letters, The American Physiological Society, 2002, 88(17): 174102(1-4).

[12] 张超，陈建军，郭迅. 基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J]. 中南大学学报，2012, 43(3)：932-939.

(编辑 李秀敏)

Application of Ensemble Local Mean Decomposition and Permutation Entropy in Rolling Bearing Fault Diagnosis

LI Wei-juan1, CHEN Shuai2, ZHANG Chao2

(1.Baotou Vocational Technology College, Baotou Inner Mongolia 014030, China; 2.School of Mechanical and Engineering ,Inner Mongolia University of Science and Technology, Baotou Inner Mongolia 014010,China)

Aiming at the problem that the bearing fault signal was submerged by strong background noise so that it was difficult for the traditional envelope demodulation method to extract fault features, a method of bearing fault diagnosis ,which is based on ensemble local mean decomposition(ELMD) and permutation entropy(PE) was proposed. First, bearing vibration signal was decomposed into a series of narrow band product functions(PFs) using ELMD method. Then, the PE value of PFs was calculated to construct high-dimensional feature vectors. Finally, the high-dimensional feature vectors were transformed as input of multi-fault classifier to identify bearing fault types. The experimental results indicated that ELMD method can restrain the mode mixing effectively， permutation entropy distribution of PF components can response signal features under different working status and the intelligent diagnosis approach based on ELMD and permutation entropy can identify the operating conditions and fault types of bearing accurately.

permutation entropy; ELMD; high-dimensional feature vectors; mode mixing; fault diagnosis

1001-2265(2016)12-0088-04

10.13462/j.cnki.mmtamt.2016.12.024

2016-04-14；

2016-04-28

国家自然科学基金资助项目(51565046)；内蒙古自然科学基金资助项目(2015MS0512)；内蒙古高等学校科学研究资助项目(NJZY146)

李伟娟(1984—)，女，内蒙古赤峰人，包头职业技术学院讲师，工程师，硕士，研究方向为数控技术和机电系统故障诊断，(E-mail) bzylwjuan @163.com；通讯作者：陈帅(1990—)，男，安徽安庆人，硕士研究生，研究方向为机电系统智能诊断，(E-mail)1054543069@qq.com。

TH165；TG65

A