基于威布尔分布模型及小子样增广的滚动直线导轨副可靠性试验研究*

李 隽，欧 屹，韩 军

(南京理工大学 机械工程学院, 南京 210094)

基于威布尔分布模型及小子样增广的滚动直线导轨副可靠性试验研究*

李 隽，欧 屹，韩 军

(南京理工大学 机械工程学院, 南京 210094)

针对我国滚动直线导轨副可靠性试验存在的问题，结合机械产品本身的试验特性和失效特性，提出了基于威布尔分布模型和小子样数据样本增广及分析方法。选取一家导轨产品开展了加速寿命试验，得到该款导轨产品的威布尔分布函数和概率密度函数，方便分析研究，为以后进行导轨可靠性试验分析样本提供了一种思路。

滚动直线导轨副；加速寿命试验；威布尔分布；小子样

0 引言

机械可靠性是指机械产品在规定的使用条件下、规定的时间内完成规定功能的能力[1]。对于机械产品来说，传统的电子产品可靠性试验与分析方法并不能完全适用。日本工程师额田启三[2]就曾提出机械产品的可靠性研究不适合通过大样本的可靠性试验一次性给出结论的方法，而适合采用少量样本长期进行研究。

针对机械产品本身的试验特性和失效特性，W. J. Bochi[3]通过研究提出机械零件的失效概率密度近似服从指数分布的理论；也有不少学者[4]指出，机械产品的可靠性模型更接近于服从对数正态分布或者威布尔分布。根据滚动直线导轨的应力类型和以疲劳磨损为主要失效形式的失效机理，对于滚动直线导轨其特征寿命就是平均故障间隔时间，所以一般不完全符合指数分布和正态分布。而实践证明，威布尔分布可以用来描述各种因素对机械零件疲劳寿命的影响[5]，但我国在这方面仍然缺乏结合具体实验作为支撑的样本分析及处理。

本文在可靠性试验的基础上，得到了故障数据和失效样本，对故障数据虚拟增广得到多组故障数据，具有很强的工程性，可以借鉴应用到无故障的可靠性试验结果分析中去，以区分不同产品在功能可靠性试验中的质量状况。同时，随着滚动直线导轨副功能可靠性试验的深入开展，试验方案的更加优化，可以获取更多的故障样本，从而验证结果的准确性，拓宽功能可靠性试验的意义。

1 威布尔分布及小子样分析方法

1.1 威布尔分布模型的建立

威布尔分布是一种应用广泛的分布模型。研究表明，很多电子或机械产品都服从威布尔分布[6]。威布尔分布是含有三参数的寿命分布，可以全面的描述不同产品的分布状态，并且在参数不同时威布尔分布可以转化为指数分布和正态分布，应用非常广泛。威布尔分布可以从最弱环节模型中导出，该模型指出，故障发生在产品构成中的最弱部位，则该部位的寿命就决定了整个系统的寿命[7]。实践证明，一般由于某个局部失效而导致系统失效的元件设备等都可近似看作服从威布尔分布。一般来说金属材料产品(如轴承)的疲劳寿命就是服从威布尔分布。同样的，滚动直线导轨副也可认为服从威布尔分布。故假设滚动直线导轨的寿命分布服从威布尔分布，选取威布尔分布作为寿命特征的研究模型。

威布尔的分布函数为：

F(t)=1-e-(t-γη)m, t≥0

(1)

密度函数为：

f(t)=mη·-(t-γη)m-1·e-(t-γη)m,t≥0

(2)

式中，η为尺寸参数，m 为形状参数，γ 为位置参数。

令γ =0，可将式(2)简化为两参数的威布尔分布，记为W(m,η)

f(t)=mη·(tη)m-1·e(tη)m),t≥0

(3)

分析可得，当形状参数m不同时，其分布类型也不同。当m<1时，早期失效较多；当m=1时，分布即为指数分布；当m>1时，密度函数呈单峰状；当m≥3时，分布呈渐对称状，近似于服从正态分布。而尺寸参数就是试验产品的特征寿命。

根据定义，可以计算得到两参数威布尔分布的以下函数：

失效率函数:

λ(t)=mηmtm-1

(4)

平均寿命:

E(T)=ηΓ(1m+1)

(5)

式中，Γ(1m+1)是伽马函数，对应数值可以查表得到。

可靠寿命:

t(R)=η(-lnR)1/m

(6)

特征寿命:

t(e-1)=η

(7)

可靠度函数：

R(t)=1-F(t)=e-(tη)m

(8)

对可靠度函数式(8)两边同时取对数后得：

-lnR(t)=(tη)m

(9)

对式(9)再次两边取对数得：

ln[-lnR(t)]=m[lnt-lnη]

(10)

根据逆幂律模型公式，令：x=lnt

y=ln[-lnR(t)]

(11)

则式(11)可转化为y=mx-B

其中，

B=mlnη

(12)

上述过程是威布尔模型的线性化过程，称为威布尔变换。

根据式(12)可见威布尔分布函数在x=lnt,y=ln[-lnR(t)]时，呈一条直线的分布，直线的斜率就是形状参数m。

1.2 基于恒加试验威布尔分布的数据分析

在恒定应力加速寿命试验的基础上，对服从威布尔分布的产品试验数据进行分析，首先要满足三个假设。

假设1：分布相同

产品在试验设定的加速应力水平S1，S2，S3…Sn下以及在正常应力水平S0时均服从布尔分布；

假设2：失效机理相同

产品在试验设定的加速应力水平S1，S2，S3…Sn下以及在正常应力水平S0时产品失效机理相同。威布尔分布式中形状参数m反映了产品失效机理，该假设也意味着分布形状参数m相同；

假设3：加速模型

产品特征寿命η和应力水平Si之间服从加速模型

lnη=a+bφ(Si)

(13)

式中，a，b为待估参数，φ(Si)是已知函数。

在这三条假设的基础上，已知产品服从威布尔分布，在恒加试验获得的产品的寿命数据t1≤t2≤…≤ti可以写成与可靠度的数组：

(tn，n) n=1,2,…i

(14)

这里Rn的可靠度可通过失效频率取估计值，但此估计往往是偏高估计，故在实际使用中一般使用失效概率的无偏估计得到可靠度的估计值：

n=1-Fn=1-(n/i+1) n=1,2,…i

(15)

然后利用威布尔变换，将数组转化为：

(x1,y1),(x2,y2),…,(xn,yn)

(16)

将所得的数据绘制在坐标系下，得到威布尔概率纸图。若该产品寿命服从威布尔分布，则其在威布尔概率图纸上的分布应成一条直线。

1.3 小子样条件下的可靠性试验分析

对于滚动直线导轨副产品，由于价格较昂贵，试验周期较长，一般不可能选取较大样本量进行试验。因此，需要找到一种适合导轨产品的小子样可靠性评价方法[8]。对于小子样数据的分析和处理，前人的基本方法都是根据经验的累积分布产生随机样本，从而对样本量进行增广。但是这种方法通常也需要10个或以上的样本量。

针对样本量往往小于等于5的极少样本数的导轨副加速寿命试验进行研究，首先也是要对样本量进行虚拟增广[9-10]。样本虚拟增广的实质是产生一组随机数组，使得该数组与原试验数据服从同样的分布形式，同时增广后的样本应满足增广子样的均值和标准差与原试验样本或类似产品的经验值相等。

假设原始样本数为n=1，需要把样本量增广至m。

可通过以下经验公式进行虚拟增广：

T=T0±[0.106×(i-1)2+c]σ i=1,2,3…m/2

(17)

式中，T为虚拟后的样本值；T0为样本均值；σ为样本标准差或类似件产品试验标准差；c为待定常数系数。

假设在原有样本数据T0的基础上增广样本量至10个，那么增广后的样本T1,T2,T3,…,T10分别为式(18)：

T1=T0-[0.106×42+c]σ
T2=T0-[0.106×32+c]σ
T3=T0-[0.106×22+c]σ
T4=T0-[0.106×12+c]σ
T5=T0-cσ
T6=T0+cσ
T7=T0+[0.106×12+c]σ
T8=T0+[0.106×22+c]σ
T9=T0+[0.106×32+c]σ
T10=T0+[0.106×42+c]σ

(18)

又根据虚拟增广方法成立的条件，增广后的样本均值和方差应与之前相同，所以可立方程组：

(19)

求解可得c=0.135，将c代入公式求T1,T2,T3,…,T10得，可以得到增广后的样本。

2 滚动直线导轨副加速寿命试验

2.1 滚动直线导轨副可靠性试验系统

加速寿命试验在滚动直线导轨副可靠性试验台上进行，试验台结构如图1所示。

图1 导轨可靠性试验台示意图

本设计目的是对导轨副的功能可靠性特征进行试验和测量，可以对导轨副产品进行可靠性摸底试验、可靠性增长试验以及可靠性鉴定试验等[11]。滚动直线导轨可靠性试验台是通过对导轨副进行模拟实际工况的加载和跑合，试验过程中记录振动、噪声、负载等的信号变化情况以及跑合过程中被测导轨副出现的实验现象以及故障信息，从而通过对试验样本和试验数据的分析处理结果对被测导轨的可靠性做出相应验证、测定或评估。

2.2 加速寿命试验过程及记录

试验样本选取某厂家型号为2-35-3000的导轨，在负载为30%额定动载荷、速度为80m/min条件下，在452km时出现反相器破裂、滚珠掉落的不可维修故障。跑合过程中噪声值逐渐增大，最后在里程450km左右出现减小，分析其原因是试验后期滑块内部滚珠和滚道出现疲劳剥落，磨损发热严重，导致反相器灼烧破坏，滚珠脱落，最终滑块脱离加载装置；拆卸滑块后发现滑块内滚道和滚珠均出现不同程度疲劳点蚀，此时试验终止；试验阶段共出现四次故障，并通过维修后继续试验，试验记录汇总如表1。

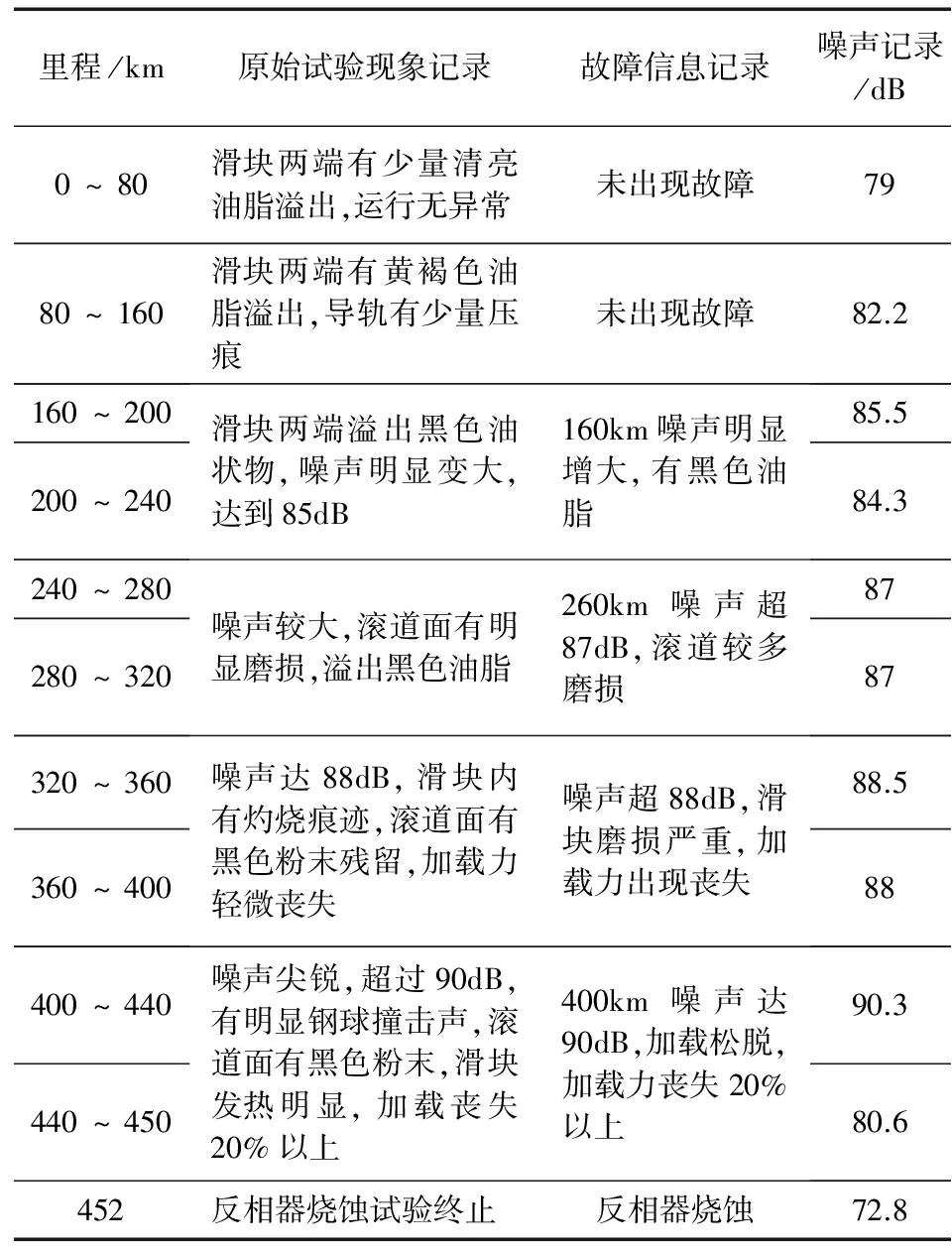
表1 试验记录汇总

在160km处噪声明显增大，滑块内有大量黑油，此时进行清洁滑块，添加润滑脂的工作；进行260km时，噪声超过87dB，滚道出现较多磨损及压痕，340km开始，噪声超过88dB，滑块磨损严重，加载力出现丧失，此时进行了重新加载并添加了润滑脂，400km时加载力丧失20%以上，452km反相器烧蚀破坏、滚珠脱落。

滚动直线导轨副额定寿命L计算的基本公式为[11]：

L=fhftfcCfwPc350km

(20)

将上述故障发生时的里程换算为常规载荷下的跑合里程，负载为30%额定动载荷，可以得到折合常规载荷跑合里程为4320km、7020km、9180km、10800km、12204km，进而算出故障间隔时间，方便进行数据处理。

在整个试验过程中，滑块两端不断有油脂流出，噪声值出现了由低到高再降低的过程，在试验后期，滑块反相器烧蚀，其主要原因有预紧力和负载过大导致的摩擦力过大加剧导轨发热；其次润滑条件不佳或滑块中进入外界杂质也会导致摩擦磨损加剧导致温升异常；运行速度过快、导轨频繁反向也会使滑块发热过快以及散热不及时导致反相器烧蚀。噪声值在里程440km左右出现减小，原因是滑块内部滚珠和滚道出现疲劳剥落，导致加载松脱，最终滑块脱离加载装置，不足以支撑试验继续进行。为进一步分析确认该导轨样件的状态，在实验结束后对滑块进行拆解，发现此时滚珠及滑块内部滚道都出现不同程度疲劳点蚀现象，通过整个试验过程可以直观反映出导轨的该可靠性能。

接下来可以通过对不同厂家在相同试验条件下的试验结果进行比较，得到主流导轨的可靠性试验里程数，观察滚动体及溢出物等方面的不同，从而进行结果的验证，也为验证数据处理结果提供帮助。

3 加速寿命试验结果分析

通过试验记录结果可得，试验中的故障间隔时间分别为{4320，2700，2160，1620，1404}。可以计算得故障间隔时间的平均值为2440.8，标准差为1041.7。

按照小子样分析方法对样本进行虚拟增广，获得10个随机数，使这组数列满足T0=2440.8，标准差为S=1041.7，并且服从威布尔分布。于是可得增广样本数据{Ti}，i=1,2,…10为：{533.5，1306.4，1858.5，2189.8，2300，2440.8，2581.4，2691.2，3247.1，3575.2，4348.2}。

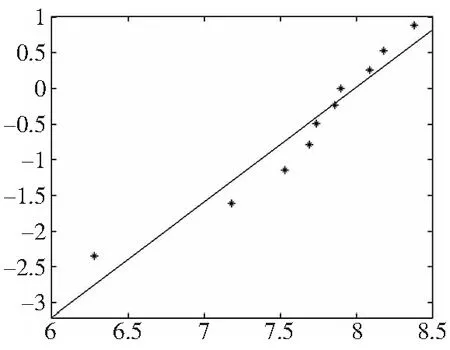
图2 MTBF数据的威布尔概率纸图

可写出威布尔变换函数式为y=1.6087x-12.8543，可计算得尺寸参数η=2952.77，形状参数m=1.6087；此时可写出威布尔分布的分布函数为:

F(t)=1-e-(t2952.77)1.6087

威布尔分布图如图3。

图3 威布尔分布图

概率密度函数为：

f(t)=4.21×10-6·t0.6087·e-t2952.771.6087

概率密度图如图4。

图4 威布尔分布概率密度图

可靠度函数为：

R(t)=1-F(t)=e-t2952.771.6087

失效率函数为：

λ(t)=m/ηmt(m-1)=4.21×10-6t0.6087

同时可得到该型号导轨的其他寿命指标：

威布尔分布特征寿命：

t(e-1)=η=2952.77km

平均寿命E(T)为：

E(T)=ηΓ(1m+1)=2645.98km

式中,Γ函数值可通过查表得到。

中位寿命t(0.5)为：

t(0.5)=η(ln2)1/m=2351.17km

可靠寿命t(R)为

t(R)=η(-lnR)1/m

由此可得，该型号导轨MTBF与可靠度的对应关系如表2所示。

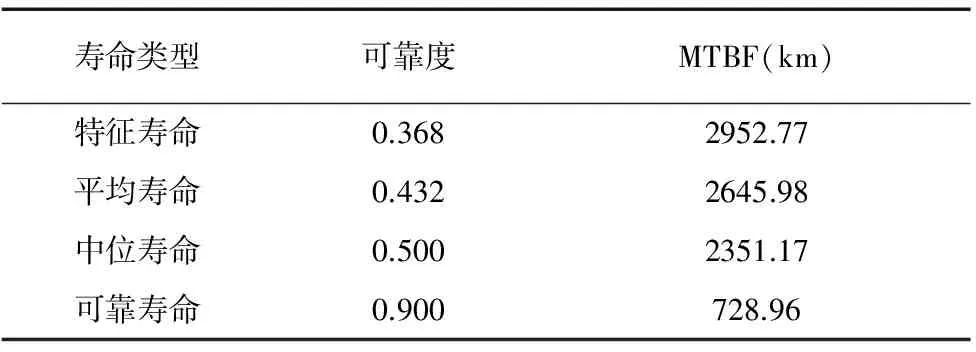
表2 某厂家2-35-3000型导轨MTBF与可靠度关系

在恒加寿命试验的基础上，通过小子样的虚拟增广得到一组样本，通过载荷的等效计算可得，在正常工况下，该型号导轨产品可靠性特征如表2。在可靠度为90%的情况下，平均故障间隔时间MTBF可达到728.96km。

进一步分析，根据公式(20)可反推得到额定动载荷C的计算公式为：

C=fwPcfhftfc·3L50km

(21)

故在该加速寿命试验的基础上得到导轨额定寿命试验值，进而可通过寿命公式反推得到导轨额定动载荷的计算值。

以该加速寿命试验为例，导轨在30%C、80m/min的加速工作状态下，里程为452km时滑块内部出现严重破坏试验终止；经分析，在试验进行至340km时，噪声明显超出正常范畴，磨损严重，滑块内滚道和滚珠已开始出现疲劳剥落，故此处导轨寿命以340km描述。根据试验条件可知：

fh=1，ft=1，fc=1fw=1.6，
Pc=30%C0，L=340km

C0为产品手册给定额定动载荷值。根据公式(21)可知：

C=1.6×30%C03340/50=0.91C0

由此可知，导轨额定动载荷试验值要小于理论计算值。若进行多组试验，经过威布尔分布函数的分析计算并得出概率函数，计算出导轨寿命值，通过小子样增广，可在此基础上的到多组对应导轨额定动载荷值，最后可对比理论计算值，可以对额定动载荷C进行一定的优化和修正。

4 结束语

针对国内滚动直线导轨副产品在可靠性方面相对落后，结合试验分析案例较少的现状，对导轨可靠性的分析和评价方法进行了研究。在威布尔分布模型增广的基础上，提出了符合导轨寿命分布的模型，并基于加速寿命试验提出了一种基于小子样的导轨副产品可靠性分析方法。选择一个厂家的导轨副产品进行了加速的全寿命试验，按照产品失效服从威布尔分布的特点，对试验结果进行了分析处理。在此基础上，考虑到当前寿命和额定动载荷的理论计算方法的局限性，尝试提出了基于试验的公式修正方法，为滚动直线导轨副可靠性的分析提供了基础，后续需要继续进行大量试验进行相关结论的验证。

[1] 张义民.机械可靠性漫谈[M]. 北京: 科学出版社, 2012.

[2] 葛甜. 刀库及机械手可靠性综合实验及评估方法研究[D]. 南京：南京理工大学，2012.

[3] 凌丹, 何俐萍, 许焕卫, 等. 基于威布尔分布的疲劳剩余寿命可靠性预测方法[J]. 机械设计, 2011(7):50-54.

[4] 陈炳琨.数控机床可靠性试验设计及评估方法研究[D].长春:吉林大学,2011.

[5] 邹辉, 黄筱调, 洪荣晶,等. 基于两重威布尔分布的大型数控铣齿机可靠性评价[J]. 机械设计与制造, 2010(2):198-200.

[6] 徐弘博.滚动直线导轨副寿命试验台设计与试验方法研究[D].南京：南京理工大学，2013.

[7] 康献民, 赵美玲. 直线滚柱导轨副寿命试验研究[J].机电工程技术, 2013, 42(8):149-152.

[8] 汪晓洋.小样本下可靠性试验方法与数据处理的研究[D].成都:电子科技大学,2012.

[9] 黄玮, 冯蕴雯, 吕震宙. 极小子样试验的虚拟增广样本评估方法[J]. 西北工业大学学报, 2005, 23(3): 384-387.

[10] 杨志伟, 任工昌, 孟勃敏. 基于加工中心的极小子样试验评估法[J]. 制造技术与机床, 2012(2):71-73.

[11] 石田俊雄. 滚动直线导轨副可靠性试验及评估方法[D]. 南京：南京理工大学，2015.

(编辑 李秀敏)

Test Bench Optimization and a Testing Methods for Rated Dynamic Load of Roller Linear Guide

LI Jun, OU Yi, HAN Jun

(School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing 210094, China)

Aiming at the problems existing in the linear guide rail pair reliability test of China，combined with the test characteristics of mechanical product and failure characteristics，the article introduced the data analysis methods for small sample data reliability test based on the Weibull distribution model. Select one of companies and carry out the accelerated life test. Calculate the size and shape parameters of the distribution function in order to do other researches and provide a way to analyze the samples for reliability tests.

roller linear guide; accelerated life test; weibull distribution; small sample data optimization

1001-2265(2016)12-0148-04

10.13462/j.cnki.mmtamt.2016.12.040

2016-01-27;

2016-03-21

国家科技重大专项(2014ZX04011031)

李隽(1991—),男，江苏徐州人，南京理工大学硕士研究生，研究方向为滚动直线轨道副可靠性与寿命研究，(E-mail)409962647@qq.com;通讯作者：韩军(1963—)，女，南京人，南京理工大学副研究员，研究方向为精密机械测控系统，(E-mail)hanjun7045@163.com。

TH161;TG506

A