基于贝叶斯群判断理论的数控机床装配可靠性保障方法研究*

李国发，董精华，许彬彬，李 瑾，解维德，侯 超，王 剑

(1.吉林大学 a.机械科学与工程学院；b.机械工业数控装配可靠性技术重点实验室，长春 130022；2.大连机床集团有限责任公司，辽宁 大连 116000)

基于贝叶斯群判断理论的数控机床装配可靠性保障方法研究*

李国发1a,1b，董精华1a,1b，许彬彬1a,1b，李 瑾2，解维德1a,1b，侯 超1a,1b，王 剑1a,1b

(1.吉林大学 a.机械科学与工程学院；b.机械工业数控装配可靠性技术重点实验室，长春 130022；2.大连机床集团有限责任公司，辽宁 大连 116000)

为了对数控机床装配过程实施可靠性控制，提出了一种基于贝叶斯群判断理论的装配可靠性保障方法。该方法通过组织多个专家对机床装配工艺薄弱工序故障原因进行评判，得到用于确定装配工艺薄弱工序的贝叶斯群判断结果。以加工中心主轴箱装配工艺为例，通过计算出每个专家的准确度及有效度，并利用加权多数原则对薄弱工序故障原因进行判断，最终确定主轴箱装配工艺的薄弱工序。将专家群判断的有效度与单个专家判断的有效度进行比较，验证了群判断的有效性高于单个专家判断的有效性。

数控机床;可靠性保障;装配工艺;贝叶斯群判断;加权多数原则

0 引言

装配是指根据产品设计的技术规定和精度要求，将构成产品的零件组合成组件、部件，直至组合成整个完整产品的过程。数控机床的功能多样，结构复杂，装配过程复杂，容易导致装配完成的机床故障频发。为此，国内机床制造企业首先从提高零部件供应商产品质量和可靠性入手，但即便使用了国外高质量高可靠性的零部件，经过工厂装配后，数控机床产品的可靠性与国外同类机床水平却有较大差距。因此，装配对于数控机床可靠性的保障具有重要意义。装配可靠性是指在规定的装配条件(包括装配技术要求)下和规定的装配时间内，装配过程达到规定可靠性指标的能力[1]。对装配可靠性进行分析与控制对于保障产品整机可靠性具有非常重要的作用,对提高机床企业市场竞争力具有重要推动作用。

目前，国内外专家在装配可靠性及装配故障方面做了许多研究，Hinckley[2]使用装配时间来定义装配复杂度，发现装配故障率与总装配时间存在正相关关系，而与装配流水线上的工位数存在负相关关系，并在此基础上提出了基于装配时间的装配复杂度函数。SU[3]等研究了用于机电产品(包括数控机床)工艺复杂度的分析方法。Suzuki T[4-5]研究了装配车间的运行可靠性，提出装配可靠性评价方法。这些研究多是从装配故障率、装配生产线等方面对装配可靠性进行研究，无法针对具体装配工艺进行判断及改进。而数控机床装配工艺FMECA是针对机床装配过程中的每个工艺步骤可能发生的故障模式、影响及其危害性，按某一标准对故障模式风险进行评测，对薄弱工艺环节采取改进措施，并跟踪改进措施的有效性，直到所有工艺故障模式风险达到预期目标，以此来保障数控机床装配过程中的可靠性水平[6]。但是，介于数控机床产品种类繁多，通常属于小批量生产，因而产生的故障数量更少。而样本数量少就会导致概率计算的准确性不高，因此对装配工艺的故障原因进行概率等级评价及量化打分比较困难。为改进以上研究存在的问题，本文提出了一种基于贝叶斯群判断理论的装配可靠性保障方法。考虑到现在机床装配可靠性领域的专家不多且单个专家的研究水平有限, 而且群判断的有效度比所有的单个判断的有效度要高[7],因此采取群判断的方法。现有的专家判断方法主要用于群决策[8]以及数据融合[9-10]等，其复杂性程度较高,而贝叶斯群判断理论的应用具有简单易行的特点。在将贝叶斯群判断理论应用在装配工艺FMECA中时，既可针对每一装配工序进行分析，又可利用专家群判断得出薄弱工序，提高了判断的准确性。最终采取改进措施，达到保障装配可靠性的目的。因此，贝叶斯群判断优势很明显。

1 贝叶斯群判断理论

1.1 贝叶斯群判断的前提条件

贝叶斯群判断在数控机床装配过程中可以用于确定装配过程中的薄弱工序。为便于专家判断，本文将故障原因分为两类，即导致薄弱工序发生的“薄弱工序故障原因”及“非薄弱工序故障原因”。

应用贝叶斯群判断理论的前提是给出需要判断的装配工序及其各个故障原因，并提供相关信息。然后所有专家根据其经验和所提供的信息，对各故障原因是否为薄弱工序故障原因进行判断。当某个工序的故障原因中出现薄弱工序故障原因时，则该工序为薄弱工序；否则，该工序不是薄弱工序。

1.2 贝叶斯群判断专家指标

为将每位专家的单个判断融为一个群判断，首先要评判单个专家的判断能力，本文引入两个指标：准确度和有效度。

(1)准确度

准确度描述了单个专家判断的准确程度，可以看作是依据该专家在以往判断中的表现给出的专家判断能力的评价，准确度具体分为：正灵敏度和负灵敏度，分别定义为：

单个专家的正灵敏度：

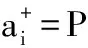
(1)

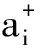
单个专家的负灵敏度：

(2)

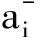
“+i”代表第i(i=1,2,3…n)个专家判断某故障原因为薄弱工序故障原因这一事件，B代表该故障原因实际上是薄弱工序故障原因这一事件；“-i”代表第i(i=1,2,3…n)个专家判断某故障原因为非薄弱工序故障原因这一事件，FB代表该故障原因实际上是非薄弱工序故障原因这一事件。

准确度指标在计算专家的判断能力方面极其重要。在实际情况中，正灵敏度指标可以通过计算该专家在以往的判断中对薄弱工序故障原因的正确判断率(正确判断的薄弱工序故障原因数与需要判断的总的薄弱工序故障原因数之比)来获得，而负灵敏度则通过对非薄弱工序故障原因的正确判断率来获得。

(2)有效度

有效度描述了专家关于某个装配工序故障原因是否为薄弱工序故障原因的判断与实际情况的符合程度，通常用条件概率来表示。

单个专家的有效度：

(3)

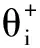
(4)

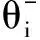
单个专家的有效度可通过贝叶斯定理计算：

(5)

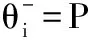
(6)

式中：P(B)代表该故障原因为薄弱工序故障原因的概率，P(FB)代表该故障原因为非薄弱工序故障原因的概率。如果没有可用的装配工序的相关信息，一般可以设P(B)=P(FB)=0.5。

1.3 贝叶斯群判断基本步骤

基于贝叶斯方法的群判断需要融合所有专家的判断，形成一组专家的群判断。考虑到单个专家判断的随机性，本文采用加权多数原则[10](WMR-Weighted Majority Rule)将这些判断的组合与专家权重相结合，然后计算出群判断的准确度和有效度。其步骤如下：

(1)利用公式(1)和(2)计算出单个专家的准确度；

(2)利用公式(5)和(6)计算出单个专家的有效度；

(3)计算专家初始权重。

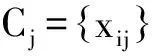
因此，在给定某故障原因为薄弱工序故障原因的概率为0.5(如果没有可用的装配工序的相关信息，一般可以设P(B)=P(FB)=0.5)的条件下,n个专家给出的第j(j=1,2…,m)个故障原因的组合的总条件概率为：

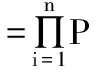
(7)

同样，在给定某故障原因为非薄弱工序故障原因的概率为0.5(如果没有可用的装配工序的相关信息，一般可以设P(B)=P(FB)=0.5)的条件下，n个专家给出的第j(j=1,2…,m)个故障原因的组合的总条件概率为：

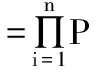
(8)

根据上述加权多数原则在进行薄弱工序故障原因判断前，有必要考虑不同专家的判断能力的影响，即赋予专家权重：

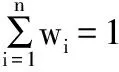
式中：wi代表第i个专家的权重。

第i个专家的初始权重可以由所有专家的准确度指标通过下式计算：

(9)

式中：

(10)

(11)

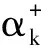
(4)综合每位专家进行群判断

如前文所述,本文利用了加权多数原则,首先定义第j个故障原因的组合Cj的加权多数原则函数WF(Cj)如下：

(12)

群判断的结果由该加权多数原则函数的取值决定：如果WF(Cj)≥0.5，则判断该故障原因为薄弱工序故障原因；反之，如果WF(Cj)<0.5，则判断该故障原因为非薄弱工序故障原因。

(5)计算群判断的准确度

群判断正灵敏度：

(13)

群判断负灵敏度：

(14)

式中：

“+”表示这组专家的群判断评定某故障原因为薄弱工序故障原因这一事件；

“-”表示这组专家的群判断评定某故障原因为非薄弱工序故障原因这一事件；

函数：

(15)

(6)计算群判断有效度：

θ+=P(B|+)=

(16)

θ-=P(FB|-)=

(17)

由前文知,有效度θ+与θ-代表了群判断的结果与实际结果的吻合概率，因此它们可以作为评价判断质量的指标。比较单个专家判断的有效度与群判断的有效度两者之间的大小关系，就可评判出哪种判断方法更有效。

2 实例分析

本文以国内某机床厂生产的某型号加工中心关键部件-主轴箱的装配工艺为例，对其应用上述的贝叶斯群判断理论进行装配工艺FMECA研究，寻找薄弱工序故障原因以确定薄弱工序。由于篇幅限制，本文组织5位专家进行判断，举例中仅列出其中5道工序的13种故障原因。具体步骤如下：

(1)给出装配工艺FMECA表

给出需判断的工序及工艺故障模式、故障原因及影响，并对故障模式以故障原因编号(见表1)。

表1 主轴箱工艺故障模式、故障原因及影响(部分)

(2)运用贝叶斯群判断理论进行判断

由前文可知，本例中并没有关于工序故障原因的相关信息，因此假设P(B)=P(FB)=0.5。在判断之前对专家进行试验训练(在已知薄弱工序故障原因的情况下测试专家的判断正确与否)，根据每位专家的表现得到各专家的准确度。根据公式(9)计算出每位专家的权重,则这5位专家的有效度可通过公式(5)和(6)可以求得，专家计算结果如表2。

表2 专家计算结果

表3列出了单个专家判断的所有组合和每一个组合的加权多数原则函数值以及对应的P(Cj|B)和P(Cj|FB)。对每一种组合Cj，由公式(12)求得WF(Cj)，根据该函数值WF(Cj)进行群判断。由公式(7)、(8)、(10)、(11)计算出P(Cj|B)和P(Cj|FB)。表中符号“+”和“-”分别表示对该故障原因是否为薄弱工序故障原因的群判断结果。

表3 群判断计算结果

由表3可知，故障原因5、6、7、11、13为薄弱工序故障原因，1、2、3、4、8、9、10、12为非薄弱工序故障原因。由于工序5、工序8的故障原因中都有薄弱工序故障原因，因此得出工序5和工序8都是薄弱工序，而工序1、工序2和工序6则不是薄弱工序。

(3)比较单个专家判断与贝叶斯群判断的有效性

由公式(13)和(14)计算群判断的正负灵敏度。

群判断正灵敏度：

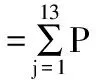
群判断负灵敏度：

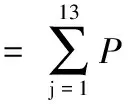
由公式(16)和(17)可得群判断的有效度为：

θ+=0.9488θ-=0.9224

将群判断的有效度与表2中各个专家的有效度进行比较可知，判断结果的有效性通过群判断获得了提高。

(4)对薄弱工序的改进措施进行跟踪评价

针对不同原因引起的各个装配工艺故障模式制定改进措施，直到该工序符合要求为止。例如：对工序8中的故障模式“导轨面的平行度不达要求”的原因“修刮不合格”，改进前评判为薄弱工序故障原因，对该工序采取了“修刮之后进行检查”的改进措施，经跟踪：该故障的发生概率降低了，专家最终评价该故障原因达到非薄弱工序故障原因的水平，这表明改进措施是很有效的。最后制定出采用贝叶斯群判断的主轴箱装配工艺FMECA表(见表4)。表中符号“+”和“-”分别表示对该故障原因是否为薄弱工序故障原因的群判断结果。

表4 主轴箱装配工艺FMECA表(贝叶斯群判断)(部分)

3 结论

(1)提出了一种基于贝叶斯群判断理论的数控机床装配可靠性保障方法。运用该方法对加工中心主轴箱装配工艺进行研究，利用贝叶斯群判断结果分析出薄弱工序故障原因，判断得到了该装配工序中的薄弱工序.本实例中，判断得出工序5和工序8为薄弱工序，而工序1,2,6则不是薄弱工序。

(2)将群判断有效度与单个专家的有效度进行比较，验证了群判断的有效性高于单个专家判断的有效性，证明了该群判断方法具有判断有效性高的特点。

(3)通过对薄弱工序的改进措施进行后续评价，可以判断改进措施是否有效。在改进装配工艺方面具有较强的工程应用价值。

[1] 邓正龙.过程系统的可靠性[M].北京:中国石化出版社,1996.

[2] Hinckley M. A global conformance quality model:A new strategic tool for minimizing defect caused by variation, error, and complexity [D]. A dissertation submitted to the Department of Mechanical Engineering of Stanford University, 1993.

[3] Su Q, Liu L, Whitney D E. A Systematic Study of the Prediction Model for Operator-Induced Assembly Defects Based on Assembly Complexity Factors [J]. IEEE Transactions on Systems, Man and Cybernetics, Part A: System & Humans, 2010, 40(1): 107-120.

[4] Suzuki T，Ohashi T，Asano M，et al. Assembly Reliability Evaluation Method (AREM)[J]. CIRP Annals-Manufacturing Technology.2003,52(1):9-11

[5] Suzuki T，Ohashi T，Asano M，et al. AREM Shop Evaluation Method[J].CIRP Annals-Manufacturing Tehnology.2004,53(1) :43-46.

[6] GJB/Z 1391-2006．故障模式、影响及危害性分析[S]．2006.

[7] 蒋平.机械制造的工艺可靠性研究[D].长沙：国防科学技术大学研究生院, 2010.

[8] Chin-Chun Lo, Ping Wang, Kuo-Ming Chao. A fuzzy group-preferences analysis method for new-product development[J]. Expert Systems with Applications, 2006, 31(4): 826-834.

[9] Xian-feng Fan, M J Zuo. Fault diagnosis of machines based on D-S evidence theory, Part 1:D-S evidence theory and its improvement[J]. Pattern Recognition Letters, 2006, 27(5): 366-376.

[10] Xian-feng Fan, M J Zuo. Fault diagnosis of machines based on D-S evidence theory, Part 2：Application of the improved D-S evidence theory in gearbox fault diagnosis[J].Pattern Recognition Letters, 2006, 27(5): 377-385.

(编辑 李秀敏)

Research of Assembly Reliability Assurance Method of CNC Machine Tools Based on Bayesian Group Decision Theory

LI Guo-fa1a,1b,DONG Jing-hua1a,1b,XU Bin-bin1a,1b,LI Jin2,XIE Wei-de1a,1b,HOU Chao1a,1b,WANG Jian1a,1b

(1 a.College of Mechanical Science and Engineering;b.Key Laboratory of CNC Equipment Reliability Technique of Machinery Industry, Jilin University, Changchun 130022, China;2.Dalian Machine Tools Group Co., LTD, Dalian Liaoning 116000,China)

In order to implement the control of the reliability of the CNC machine tools assembly process, an assembly reliability assurance method based on Bayesian group decision theory was put forward. The method was used to judge the failure causes of the weak process in the CNC machine tools assembly process, and it could get the results of Bayesian group decision theory .The results were used to determine the weak process of the assembly process. The assembly process of machining center spindle box was taken for example. By calculating the accurate degree and the effective degree of each expert and using Weighted Majority Rule, it could judge the failure causes of the weak process. Finally, it determined the weak process. The effective degree of expert group decision was compared with a single expert decision, and it is verified that the effectiveness of the group decision is higher than the effectiveness of a single expert decision.

CNC machine tools; reliability assurance; assembly process; bayesian group decision theory; weighted majority rule

1001-2265(2016)12-0152-05

10.13462/j.cnki.mmtamt.2016.12.041

2016-01-21；

2016-03-02

国家科技重大专项项目：精密卧式加工中心主轴箱加工自动线示范应用(2015ZX04005002)

李国发(1970—),男,吉林农安人，吉林大学教授, 博士，博士生导师，研究方向为数控装备可靠性技术及理论, (E-mail)ligf@jlu.edu.cn；通讯作者：许彬彬(1982—)，女，吉林大学讲师，博士，研究方向为数控装备可靠性、维修性理论，(E-mail)xubinbin@jlu.edu.cn。

TH162；TG659

A