基于SLLE算法和流形聚类分析的滚珠丝杠故障诊断*

李 善，谭继文，俞 昆

(青岛理工大学 机械工程学院，山东 青岛 266520)

基于SLLE算法和流形聚类分析的滚珠丝杠故障诊断*

李 善，谭继文，俞 昆

(青岛理工大学 机械工程学院，山东 青岛 266520)

针对滚珠丝杠故障信号非线性的特点及故障特征集中冗余信息的干扰，提出了将SLLE降维方法与流行聚类分析相结合的故障诊断方法。采集滚珠丝杠不同故障状态的振动信号和噪声信号，构造原始信号特征向量；利用SLLE算法对特征向量进行降维处理，得到筛选后的特征向量，绘制出其三维分布图；计算每种故障的聚类中心和流形距离，根据“最短距离”原则进行故障识别诊断。并通过试验及与KPCA、LLE两种诊断方法的比较，验证了SLLE降维方法与流行聚类分析相结合的故障诊断方法的有效性和识别结果的准确性。

SLLE算法；流形距离；故障诊断

0 引言

滚珠丝杠以其精度好、传动效率高等特点，广泛应用于数控机床，是机械行业使用最广的传动组件之一。但常常因为使用和维护不当，无法满足加工精度要求，甚至使数控机床出现故障和损坏。因此，及时进行滚珠丝杠故障诊断是保证数控机床正常运行和提高加工质量的重要环节。

滚珠丝杠发生故障时，其信号表现为非线性的特点，且信号特征向量维数巨大，不易进行后续诊断工作。由于传统KPCA降维方法无法保留数据原始特征的缺点，S.T.Roweis等人提出了LLE方法，该方法很好地保留了数据的原始结构，并广泛应用于人脸识别，图像处理等领域。但LLE属于非监督式降维方法，没有考虑到不同故障的分类。SLLE算法增加了样本类别信息，相比于KPCA、LLE两种方法，该方法既保留了数据原始特征、又包含故障类别的样本信息，非常适合于滚珠丝杠不同类别故障的识别与诊断。

聚类分析是模式识别领域中的常用方法之一，常用的聚类分析方法有K-均值法，模糊聚类法等。距离是描述数据间差异性的度量，传统欧氏距离无法反映聚类全局的一致性，只能反映局部数据的相似性，因此本文引入基于流形距离的聚类算法，可以放大不同流形上点的距离，同时缩小相同流形上点的距离。与传统聚类方法相比，该方法能够直观、简明的反映不同故障的分类信息。

综上，本文研究基于SLLE算法与流形距离聚类算法相结合的滚珠丝杠故障诊断方法，并通过试验予以验证。

1 SLLE算法

1.1 LLE算法介绍

LLE(Locally Linear Embedding)算法，即局部线性嵌入算法，是S.T.Roweis 等人提出的一种针对非线性信号特征的无监督降维方法。该算法较传统的核主成分分析法(KPCA)来讲，既有处理非线性数据的优点，又有线性降维方法计算性能的优越性。它不仅是数量上的简单降维，更是在高维空间信号映射到低维空间的过程中保持了原始数据性质不变，相当于数据特征的二次提取[1]。

LLE算法步骤[2]如下：

(1)寻找高维空间中每个样本点xi的k个近邻点。利用欧氏距离公式计算xi与其它样本点的距离，选取距离最近的k个样本点。

(2)计算样本点的局部重构权值wij。将每个xi用它的k个近邻点的线性组合近似表示，定义重构误差函数为：

(1)

通过将其重构误差最小化，来求得重构权值：

(2)

其中Qi为局部协方差矩阵，表示为：

QZ(WTBZijm=(xi-xij)T(xi-xim)

(3)

(3)求解xi在低维空间中的投影yi。保持权值wij不变，求得样本点投影在低维空间的值，使得低维重构误差最小，即：

(4)

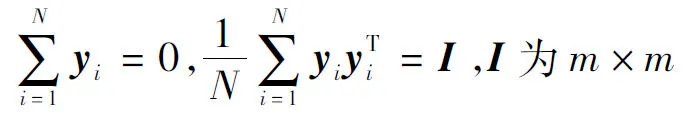
1.2 SLLE算法介绍

LLE算法的不足之处在于没有考虑数据的类别信息，因此Ridder等人提出了有监督的局部线性嵌入算法，即SLLE(SupervisedLocallyLinearEmbedding)。该算法在第一步计算欧氏距离来寻找k个近邻点时，增加了样本类别信息[3]，不同类别样本点间的欧氏距离的计算方法不同，可用于多类故障的特征提取。其余步骤与LLE算法相同。

SLLE在计算样本点间的距离时用如下公式[4]：

D′=D+αmax(D)Δ

(5)

其中D′是考虑类别信息之后计算出的距离，D是原始欧氏距离，max(D) 是不同类别之间的最大距离，α是控制样本点之间的距离参数，α∈[0,1]是个经验参数，当α=0时，SLLE算法与LLE算法相同。Δ取0或1，当样本点属于同类时，Δ=0；反之取1。

1.3 SLLE参数设置

SLLE计算过程中的近邻点个数k以及输出维数d对最后结果的影响较大。若k取值较大，则不能正确体现局部特性；若k取值较小，则不能保持原有数据的拓扑结构。k的取值要比d大一些，一般情况下取k=5～12，d可以根据实际情况来定[5]。α为经验参数，α越大，类别信息影响程度越大；反之越小。查阅相关文献，一般选取0.2～0.6[6]。

2 流形聚类分析

2.1 聚类分析原理

聚类分析(ClusteringAnalysis)是将大量样本对象按其内在相似程度划分为多个类别的过程。同一类的对象之间具有高度的相似性[7]，进行聚类分析时，主要有两种途径[8]：一是将样本对象看作是空间中的点，通过点与点之间的距离，来描述样本对象之间的近似程度，距离越小，表示对象间越相似；二是计算样本对象间的相似系数，相似系数越大，对象间越相似。

2.2 基于流形距离的聚类算法

流形距离度量方法是流形聚类分析中常用的一种方法，该度量方法可以放大不同流形上点的距离，同时缩小相同流形上点的距离。其计算距离的方法有很多种，本文采用聚类中心距离度量方法，根据“最短距离”原则，计算各样本点与各类别聚类中心的距离，相距最短的样本点就归为相应的那一类[9]。如图1所示，xi和xj分别为两类数据样本，其白色圆圈为各自类别的聚类中心，椭圆区域内的点为随机给出的待测样本点在低维空间的投影，通过计算椭圆区域内的点与各聚类中心的距离，来完成相应类别的划分。

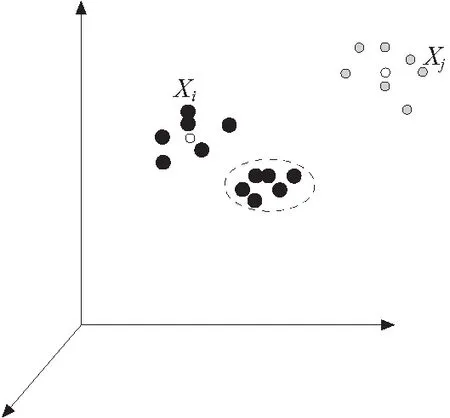
图1 距离度量方法示意图

xi与xj之间的流形距离为：

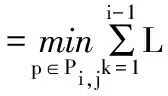
(6)

其中，p={p1,p2,…,pr}表示连接p1与pr的一条路径，Pi,j表示连接xi与xj的所有路径的集合，L(a,b)表示同一流形上两点间的的线段长度。

3 滚珠丝杠故障试验研究

3.1 故障信号的采集及特征提取

本文选用6202z型滚珠丝杠进行故障诊断试验，在丝杠前端轴承座处布置一个型号为TZ-2KA的噪声传感器，在轴承座的X、Y、Z三个方向分别布置一个型号为LC0101的加速度传感器，采集滚珠丝杠的四种不同故障状态(正常状态、丝杠弯曲、滚道磨损、滚珠破损)的振动信号和噪声信号。采样频率为512Hz，采样点数为1536。传感器分布图如图2所示。

图2 传感器分布图

用小波包分解对采集到的信号进行分解，提取每个故障信号分解后的22个时-频域特征值(8个能量特征值和峰度、偏斜度、频率方差、均方频率、重心频率、裕度因子、脉冲因子、波形因子、峰值因子、峭度因子、绝对平均幅值、方根幅值、均方根值、最大值14个时频域特征值)作为原始信号特征集，四个传感器共88维特征值。提取每种故障信号各20组，其中15组作为训练集，5组作为测试集。

3.2 特征集降维处理及性能比较

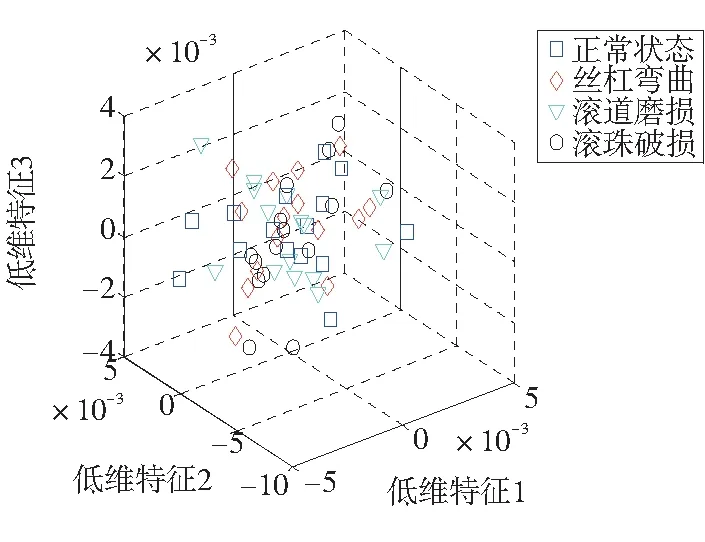
分别采用KPCA、LLE、SLLE三种方法对训练集和测试集的88维特征值进行降维处理，为方便比较，本文选取近邻点k=10，输出维数d=3。图3为三种方法降维之后的结果分布图[10]，从图中可以看出，KPCA和LLE两种降维方法的特征量有重叠现象，均不能将故障分类；而SLLE方法可以有效地分离出每一种故障，分类效果比较明显。以此验证了SLLE降维方法的可行性与有效性。

(a)KPCA降维结果

(b)LLE降维结果

(c)SLLE降维结果图3 三种方法降维结果分布图

3.3 聚类分析诊断及结果比较

对三种方法降维之后的特征训练集进行聚类中心计算，得到每一种故障类型的聚类中心，不同故障状态(记正常状态为故障A、丝杠弯曲为故障B、滚道磨损为故障C、滚珠破损为故障D)的聚类中心分别为A(-2.35，-1.58，0.59)、B(2.90，-0.31，0.94)、C(-1.23，1.67，1.53)、D(2.45，-0.58，0.86)。利用公式(6)计算出降维后的测试样本数据与聚类中心的距离，如表1～表3所示。其中，KPCA方法的诊断结果中有5组数据出现错判，诊断识别率为75%；LLE方法的诊断结果中有2组数据错判，诊断识别率为90%；SLLE方法的诊断结果中只有1组出现错误，诊断识别率高达95%，识别效果较好。

表1 KPCA方法的故障诊断结果

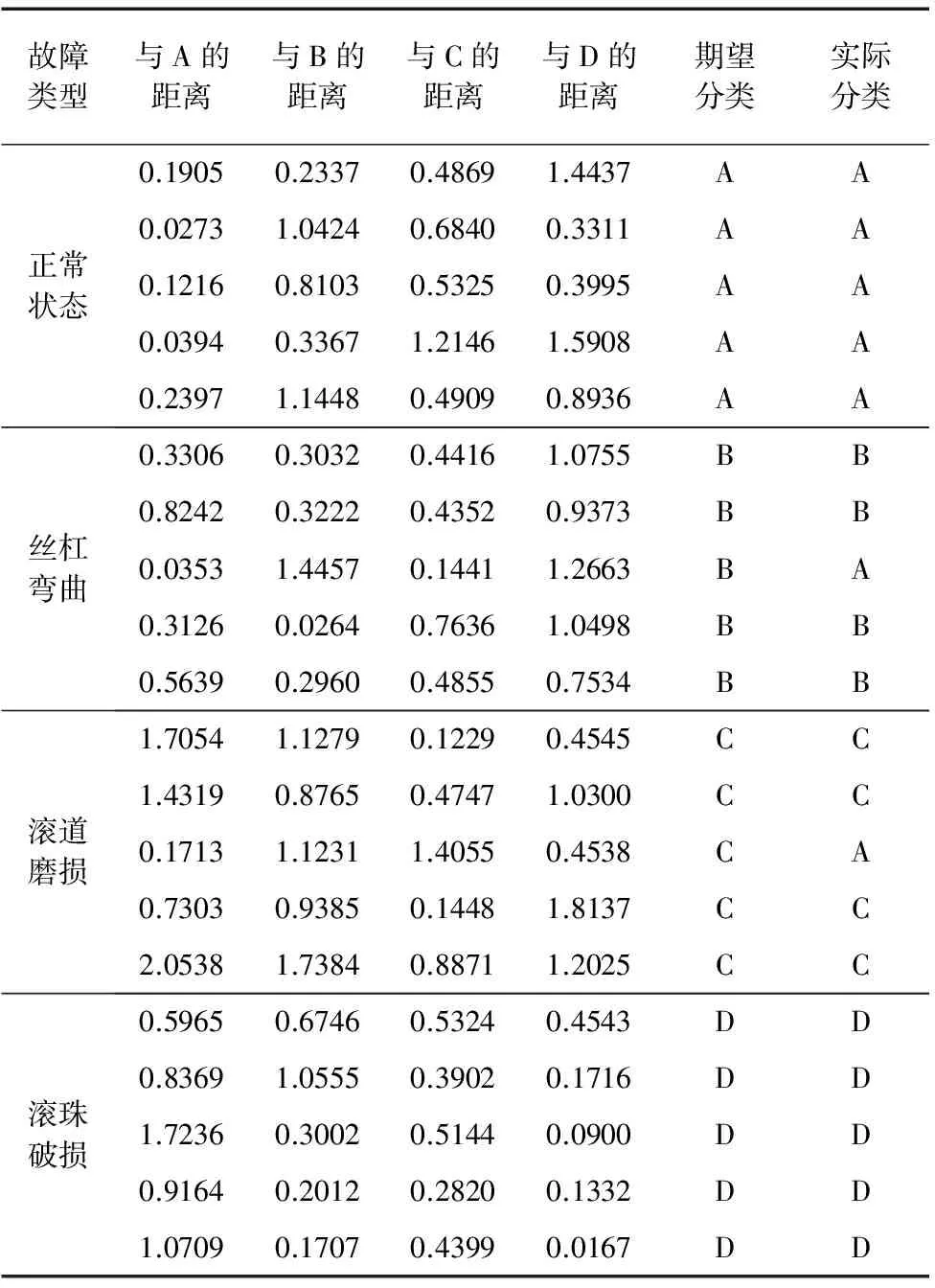
表2 LLE方法的故障诊断结果

表3 SLLE方法的故障诊断结果

4 结论

本文提出了一种将SLLE降维方法与流形距离的聚类分析相结合的故障诊断方法，应用于滚珠丝杠的不同故障状态识别。通过绘制降维后数据的三维分布图，得出SLLE降维方法的分类效果明显优越于LLE和KPCA方法。通过四种不同的丝杠故障试验，验证了聚类分析在故障诊断方面的可行性。同时，比较三种降维方法与聚类分析相结合的诊断结果，得出SLLE算法与流形聚类相结合的诊断结果最好，识别率高达95%。

[1] 张伟,周维佳,刘晓源.基于扩展LLE方法的非线性系统故障诊断研究[J].电子学报,2015,43(9):1810-1815.

[2] 张育林,庄健,王娜,等.一种自适应局部线性嵌入与谱聚类融合的故障诊断方法[J]. 西安交通大学学报,2010,44(1):77-82.

[3] 胡丹.基于改进的SLLE在地震属性优化中的研究与应用[D].成都:成都理工大学,2007.

[4] 李锋,田大庆,王家序,等.基于有监督增量式局部线性嵌入的故障辨识[J]. 振动与冲击,2013,32(23):82-88.

[5] 董安,潘宏侠,龚明.基于局部线性嵌入算法的柴油机故障诊断研究[J]. 计算机工程与应用,2013,49(22):236-240.

[6] 张石清,李乐民,赵知劲.基于一种改进的监督流形学习算法的语音情感识别[J].电子与信息学报,2010,32(11):2724-2729.

[7] 金晓慧.基于流形距离和核函数的进化聚类算法研究及其应用[D].西安:西安电子科技大学,2009.

[8] 郭启勇.流形聚类的算法研究及其应用[D]. 上海:复旦大学,2009.

[9] 贺旖琳.基于局部线性嵌入的旋转机械故障诊断研究[D].长沙:湖南科技大学,2014.

[10] 李强,皮智谋.基于FastICA_SLLE的转子系统故障诊断研究[J]. 组合机床与自动化加工技术,2014(8):105-108.

(编辑 李秀敏)

Fault Diagnosis of Ball Screw Based on SLLE Algorithm and Manifold Clustering Analysis

LI Shan，TAN Ji-wen，YU Kun

(School of Mechanical Engineering, Qingdao Technological University ,Qingdao Shandong 266520，China )

According to the nonlinear characteristics of ball screw fault signal and the interference of the fault characteristic, the fault diagnosis method based on SLLE dimension reduction method and the popular cluster analysis is put forward. Collect vibration signal and noise signal in different fault state of ball screw and structure original signal feature vector. Using SLLE algorithm to reduce the dimension of feature vectors and feature vectors are obtained. Draw its three-dimensional distribution map. Calculate the cluster centers and manifold distances for each fault and fault diagnosis based on the principle of "shortest distance". And through the experiment and comparison with KPCA and LLE two diagnostic methods, the validity and accuracy of the fault diagnosis method combined with the SLLE dimension reduction method and the popular cluster analysis method was verified.

SLLE algorithm; manifold distance; fault diagnosis

1001-2265(2016)12-0096-04

10.13462/j.cnki.mmtamt.2016.12.026

2016-01-28；

2016-02-29

国家自然科学基金项目(51075220)；山东省高等学校科技计划项目(J13LB11)；高等学校博士学科点专项科研基金(20123721110001)；青岛市科技计划基础研究项目(12-1-4-4-(3)-JCH)

李善(1990—)，女，山东莱芜人，青岛理工大学硕士研究生，研究方向为机械无损检测与故障诊断，(E-mail)1026622139@qq.com。

TH17；TG506

A