倍四元数在6R串联机器人逆解中的应用*

葛小川, 郑飂默,吴纯赟,郑国利

(1.中国科学院大学，北京 100049；2.中国科学院沈阳计算技术研究所 高档数控国家工程研究中心，沈阳 110168；3.沈阳高精数控智能技术股份有限公司，沈阳 110168)

倍四元数在6R串联机器人逆解中的应用*

葛小川1,2, 郑飂默2,3,吴纯赟1,2,郑国利3

(1.中国科学院大学，北京 100049；2.中国科学院沈阳计算技术研究所 高档数控国家工程研究中心，沈阳 110168；3.沈阳高精数控智能技术股份有限公司，沈阳 110168)

在研究了四元数性质的基础上，采用倍四元数求解6R串联机器人的逆运动学问题。将三维空间的位移表示成四维空间的双旋转，建立了倍四元数形式的机器人运动学方程，再通过消元，构造Dixon结式。最终通过求解Dixon结式求解出机器人16组解析解。最后，使用MatlabRobotics进行仿真，新方法能够求出机器人逆运动学全部解析解，而且速度比D-H方法提升了10%左右。

6关节机器人;逆运动学;倍四元数;Dixon结式

0 引言

逆运动学求解是机器人路径规划和控制的基础。逆运动学就是已知末端执行器的位姿，求解相应的关节变量的过程[1]。它实质是求解非线性方程的过程，求解过程复杂。Primrose首次论证了6R机器人的逆运动学最多有16个实根[2]，但是没有给出一般的求解过程。Lee和Liang利用14个逆运动学方程和解析方法,首次得到一般6R机器人的16组逆运动学解[3]。Manocha和Canny进一步将一元16次方程求根问题转化为24阶矩阵的特征分解问题[4],降低了对计算精度的要求。但是，这些方法都涉及到大量的矩阵运算，计算复杂而且存在奇异性的问题，不能满足实时在线控制的需求。

本文使用倍四元数建立机器人的运动学模型，将三维空间的旋转和平移运动转化成四维空间的双旋转，通过消元构建出Dixon结式，最终求解出机器人所有的关节角。新的逆运动学求解的方法消除了传统方法求解奇异性的问题，能够满足实时在线控制的需求。

1 四元数及倍四元数

四元数由一个实数和向量组成，可以空间旋转运动。四元数可以表示成：Q=q0+q1i+q2j+q3k=q0+q，表示绕着q的方向旋转q0弧度。

G=cos(θ/2)+sin(θ/2)(s1i+s2j+s3k)
H=cos(φ/2)+sin(φ/2)(s1i+s2j+s3k)

(1)

2 6R机器人运动学方程倍四元数表示

2.1 连杆变换的倍四元数表示

6R机器人的运动由6个连杆的平移和旋转运动构成，四维空间球体半径足够大，我们就可以将三维空间的位移表示成四维空间的双旋转，因此将连杆变换用倍四元数表示。

如图1表示使用D-H法建立的相邻关节i-1和i之间的关系。其中，关节i-1绕自身z轴旋转θi，平移si得到新的坐标系(i-1)′,新的坐标(i-1)′绕x轴旋转αi平移ai得到i坐标系。

图1 相邻坐标变换

得到坐标系(i-1)′的过程用倍四元数可以表示成：

z(θ,γ)=ζG(θ,γ)+ηH(θ,γ)

(2)

G(θ,γ)和H(θ,γ)分别为：

(3)

其中，γ=d/R

同理由坐标系(i-1)′向坐标i的转换过程可以标称为：

X(α,ρ)=ζG(α,ρ)+ηH(α,ρ)

(4)

(5)

(6)

(7)

ρ=a/R

R为四维空间球体的半径，根据经验公式[7]，R=L/δ1/2,L表示机器人手臂所能达到了最远距离，δ表示所要求的精度。

2.2 运动学方程的倍四元数表示

根据具有n个连杆机器人的运动学方程[8]的倍四元数表示可以得到6R机器人的一般的情况：

(8)

由于倍四元数中G和H可以分开计算，公式(9)也可以写成：

G=G(θ1,γ1)G(α1,ρ1)G(θ2,γ2)G(α2,ρ2)…
G(θ5,γ5)G(α5,ρ5)G(θ6,γ6)G(α6,ρ6)

(10)

H=H(θ1,γ1)H(α1,ρ1)H(θ2,γ2)H(α2,ρ2)…
H(θ5,γ5)H(α5,ρ5)H(θ6,γ6)H(α6,ρ6)

(11)

3 PUMA机器人倍四元数逆运动学分析

PUMA机器人的机械手臂构成一个开式运动链。它由一系列连杆通过转动关节串联而成，关节的相对转动带动连杆运动[9]。PUMA机器人由6个连杆组成，是一个典型的6自由度的串联关节机器人，它的关节结构如图2所示。D-H参数能够很好的描述PUMA机器人的各关节之间的几何关系，机器人逆运动学实质上就是通过运动学方程反解出相邻关节关节角θi的过程。PUMA机器人的D-H参数如表1所示。

图2 PUMA机器人关节结构简图

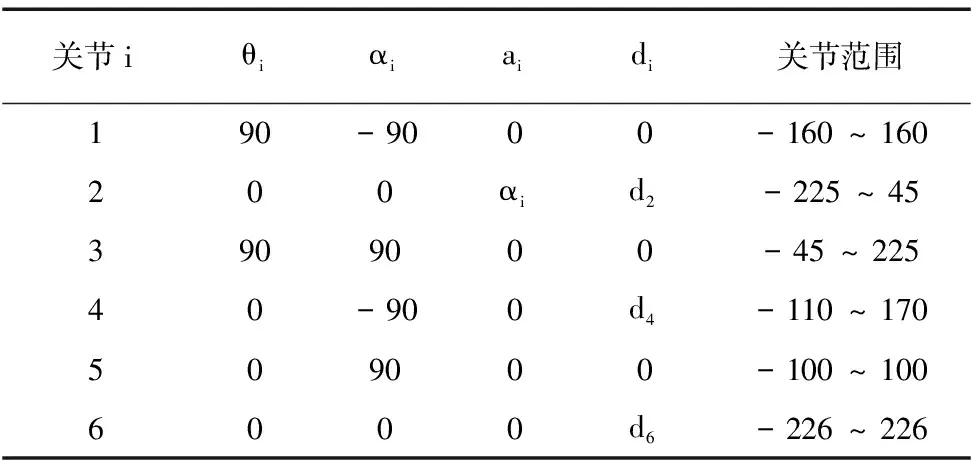
关节iθiαiaidi关节范围190-9000-160～160200αid2-225～453909000-45～22540-900d4-110～170509000-100～1006000d6-226～226

3.1 运动学建模

由公式(15)和(16)得到6自由度串联机器人的运动学方程，令：

(12)

(13)

(14)

(15)

3.2 求解

6R机器人的运动学可以表示成公式(10)和公式(11)分离变量得：

(16)

(17)

对以上的式子进行计算，对应的项相等得到8个式子：

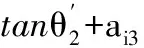
bi1y1+bi2y2+bi3y3+bi4y4

(18)

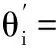
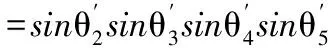
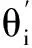
(19)

式中,ci为机械人结构所决定的已知参数。

消去θ3,θ4,θ5，将式(19)除以k

ci1+ci2u+ci3v+ci4uv+ci5w+ci6uw+

ci7vw+ci8uvw+ci9x+ci10ux+ci11vx+ci12uvx+

ci13wx+ci14uwx+ci15vwx+ci16uvwx=0

(20)

为了消去v,w,x设u为常数，定义方程：

(21)

根据文献[11]使用Dixon结式进行消元，首先构造如下方程：

(22)

展开然后以矩阵的形式重写为：

(α2β,αβ,β,α2,α,1)D6×6(x2w,xw,v,x2,x,1)=0

(23)

3.3 求解过程

(1)求解θ2

矩阵D6×6的第2列和第5列的每一个元素都能写成如下形式：

a+bu+cu2+du3+eu4

(24)

其中a,b,c,d为系数，且发现有b=d,a+e=c成立。因此(24)可以化简为：

(u2+1)(ew2+bw+a)

(25)

这样第2和第5列可以提取出(u2+1)并把它删除掉。

然后把矩阵D6×6的第3列减去第1列、第6列减去第4列，重新得到的第3列和第6列同样具有式(24)的形式且系数满足相同的关系。因此，同样把两列分别提取(u2+1)并把它删除掉。经过以上处理新的矩阵D6×6的每一列关于u的最高次数分别为4,2,2,4,2,2。

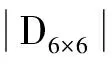
θ2=2arctanu

(26)

得到θ2的值。

(2)求解θ3,θ4,θ5

将u带入式子：

D6×6(x2w,xw,w,x2,x,1)=0

(27)

得到6个关于x2w,xw,w,x2,x的方程。从中任取5个方程，把x2w,xw,w,x2,x当做该线性方程组的5个未知数，求解出w和x。

然后把w和x带入到(20)中的任意一个可以得到v。

再用θ3=2arctanv,θ4=2arctanw,θ5=2arctanx求解出θ3,θ4,θ5。

(3)求解θ1,θ6

把θ2,θ3,θ4,θ5带入到(18)中可以计算得到y1,y2,y4。

4 实例

这里采用文献[12]的数据对上述的求解过程进行对比验证。6R机器人的结构参数和位置参数为：

通过正向运动学可以计算出机械手臂的末端位姿的矩阵表示为：

使用倍四元数表示运动学方程：

通过以上计算过程使用Matlab，最终得到16组关节角。反解结果中2组为实数解。第1组解和初值是一样的。把表中其余结果正向运动学方程进行正解验算，结果是正确的。

为了验证倍四元数方法对于速度上的提升，我们构造10组关节角(di,ai,αi同上)，分别使用D-H方法和本文提出的方法，计算出末端位姿，然后再反向求出关节角，两种方法的计算时间如图3所示。倍四元数的方法较D-H法速度上提高了10%左右。

图3 倍四元数方法和D-H方法求解速度比较

5 结论

本文针对传统D-H方法求解机器人逆运动学求解复杂，存在奇异解的问题，提出采用倍四元数表示6R机器人，并应用于PUMA机器人运动逆解中，通过消元和构造Dixon结式最终获得PUMA机器人全部的解析解。实验表明新方法计算过程简单，速度较D-H方法有很大程度的提高。该方法有存在一定的问题，比如，该方法是够适合用于机器人参数辨识有待验证，速度提升不是特别的明显等。

[1] 龚星如.六自由度工业机器人运动学标定的研究[D].南京:南京航空航天大学,2012.

[2] 张忠海, 李端玲.串联机构运动学反解的D-H四元数方法[J]. 农业机械学报, 2014, 45(3):299-304.

[3] 倪振松, 廖启征, 吴莘馨.基于四元数矩阵与Groebner基的6R机器人运动学逆解算法[J]. 清华大学学报(自然科学版), 2013,53(5): 683-687.

[4] 宋婧, 方康玲.基于倍四元数的机器人逆运动学分析[J]. 机械与电子, 2010(12): 67-69.

[5]NielsenJ,BRoth.OntheKinematicAnalysisofRoboticMechanisms[J].InternationalJournalofRoboticsResearch, 1999,18(18): 1147-1160.

[6] 方俊珊, 刘华山,孙培德.基于分块矩阵的6R机器人实时逆解算法[J]. 燕山大学学报, 2012,36(2): 119-125.

[7]PereiraVF,etal,AQualitative-ProbabilisticApproachtoAutonomousMobileRobotSelfLocalisationandSelfVisionCalibration[C].2013BrazilianConferenceonIntelligentSystems(Bracis), 2013: 157-162.

[8] 陈爱,冯桑,何春,等.基于四元数的6R串联机器人运动学逆解应用[J]. 机电工程技术, 2013,42(9): 5-10.

[9] 董明晓, 周以齐, 张明勤.PUMA机器人逆运动学求解新方法[J]. 组合机床与自动化加工技术, 2000(10):21-23.[10] 乔曙光.6自由度串联机械手位置逆解新方法[D].北京:北京邮电大学,2008.

[11] 乔曙光, 廖启征, 黄昔光.倍四元数及其在串联机构运动分析中的应用[J]. 机械设计与制造, 2008(2):36-38.

[12]HustyML,MPfurner,HPSchrocker.Anewandefficientalgorithmfortheinversekinematicsofageneralserial6Rmanipulator[J].MechanismandMachineTheory, 2007,42(1): 66-81.

(编辑 李秀敏)

Application of Double Quaternion in the Inverse Kinematics of 6 R Serial Robots

GEXiao-chuan1,2,ZHENGLiao-mo2,3,WUChun-yun1,2,ZHENGGuo-li3

(1.UniversityofChineseAcademyofSciences,Beijing100049，China；2.NationalEngineeringResearchCenterForHigh-EndCNC,ShenyangInstituteofComputingTechnology,ChineseAcademyofSciences,Shenyang110168,China)

Theinversekinematicsofageneral6Rserialrobotshasmuchdifficultytobesolvedandamountofcomputations.Also,itexistssingularsolution.Weusesdoublequaterniontodealwiththeproblem.Thedisplacementinthreedimensionscanbeconvertedtodoublerotation,wecanbuildkinematicsequationofrobotsintheformofdoublequaternion,theneliminateandbuildDixonresultantmatrixandfinallywegettheallthe16closed-formsolutions.Atlast,weverifyournewmeansusingmathroboticstoolbox.Wegetallthesolutionscorrectlyandimproveabouttenpercentcomparingtod-hmeansinspeed.

6Rrobot;inversekinematics;doublequaternion;Dixonresultant

1001-2265(2016)12-0016-04DOI:10.13462/j.cnki.mmtamt.2016.12.005

2016-02-26；

2016-03-31

国家科技重大专项：国产高档数控机床、系统及其技术在航空领域的综合应用验证及工艺研究(2014ZX04001051)

葛小川(1990—)，男，河南商丘人，中国科学院大学硕士研究生，研究方向为机器人机构学，(E-mail)gexiaochuan122@126.com。

TH165;TG

A