结式循环矩阵的运算及性质

刘兴祥，张 宇，王 姣

(1.延安大学 数学与计算机科学学院，陕西 延安 716000；2.西北农林科技大学 理学院，陕西 咸阳 712000；3.西安建筑科技大学 信息与控制工程学院，陕西 西安 710000)

循环矩阵是一类特别重要的特殊矩阵，它的应用[1-5]也极其广泛，因为循环矩阵的特殊性质以及特殊结构，所以对循环矩阵的性质和应用的研究及推广[6-8]非常有必要。结式循环矩阵作为循环矩阵的一种，在此之前，不少学者已经研究了结式循环矩阵的逆与广义逆。本文将结式循环矩阵与多项式理论结合起来，进一步研究结式循环矩阵的更多性质，给出了结式循环矩阵的运算及性质。

1 预备知识

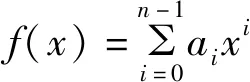
f(x)u(x)+g(x)v(x)=d(x)。

2 结式循环矩阵的性质

定义2.1 矩阵A，B具有相同的循环因子，称矩阵A，B为同型结式循环矩阵。

定义2.2 设矩阵A，B均为结式循环矩阵，其中

矩阵A+B=

定义2.3 设矩阵A，B均为结式循环矩阵，其中

矩阵A-B=

定义2.4 设矩阵A，B均为结式循环矩阵，其中

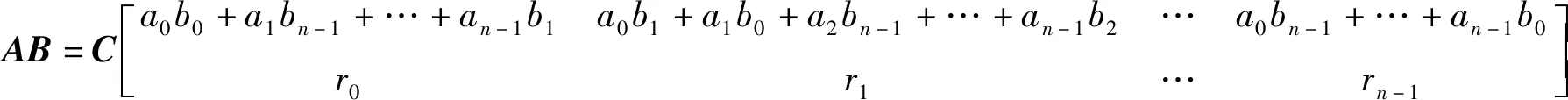
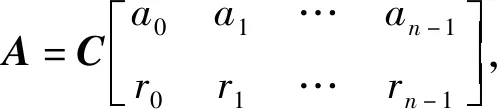
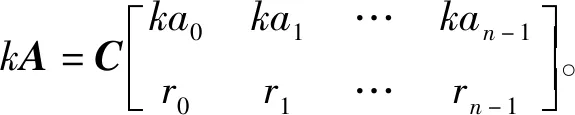
性质2.1 设矩阵A，B为n阶同型结式循环矩阵，则矩阵A+B仍为结式循环矩阵。

由定义2.2得矩阵

则矩阵A+B的特征多项式为

由定义2.2得

a0E+a1P+a2P2+…+an-1Pn-1+

b0E+b1P+b2P2+…+bn-1Pn-1=

(a0+b0)E+(a1+b1)P+(a2+b2)P2+…

+(an-1+bn-1)Pn-1，

所以矩阵A+B为结式循环矩阵。

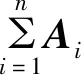
性质2.2 设矩阵A，B为n阶同型结式循环矩阵，则矩阵A-B仍为结式循环矩阵。

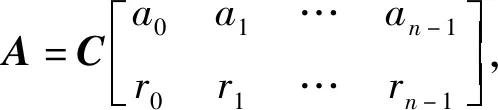
由定义2.3得矩阵

则矩阵A-B的特征多项式为

由定义2.3得

a0E+a1P+a2P2+…+an-1Pn-1-

b0E+b1P+b2P2+…+bn-1Pn-1=

(a0-b0)E+(a1-b1)P+(a2-b2)P2+…

+(an-1-bn-1)Pn-1，

所以矩阵A-B为结式循环矩阵。

推论2.2 设矩阵A1，A2，…，An为同型结式循环矩阵，则矩阵A1-A2-…An仍为结式循环矩阵。

性质2.3 设矩阵A为结式循环矩阵，则矩阵kA仍为结式循环矩阵。

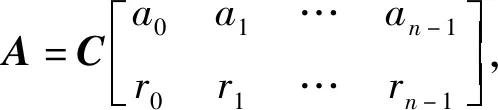
由定义2.5得矩阵

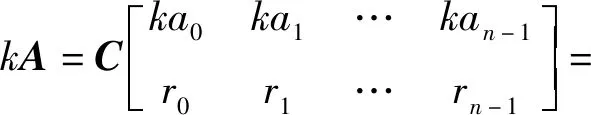
ka0E+ka1P+ka2P2+…+kan-1Pn-1=

(ka0)E+(ka1)P+(ka2)P2+…+

(kan-1)Pn-1，

所以矩阵kA仍为结式循环矩阵。

推论2.3 设矩阵A1，A2，…，An为n阶同型结式循环矩阵，k1，k2，…，kn为实数，则矩阵k1A1±k2A2±…±knAn仍为结式循环矩阵。

证明由推论2.1、推论2.2及性质2.3可得。

性质2.4 设矩阵A，B为n阶同型结式循环矩阵，则矩阵AB也是结式循环矩阵，且AB=BA。

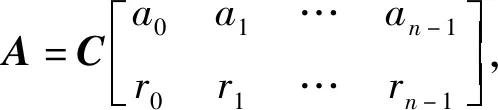
且Pn=E，Pn+1=P，…，P2n-2=Pn-2。

由引理1.2得

A=a0E+a1P+a2P2+…+an-1Pn-1，

B=b0E+b1P+b2P2+…+bn-1Pn-1，

则AB=(a0E+a1P+a2P2+…+an-1Pn-1)·

(b0E+b1P+b2P+b2P2+…+bn-1Pn-1=

(a0b0)E+(a0b1+a1b0)P+…+

(an-1bn-1)P2n-2=

=(b0E+b1P+b2P2+…+bn-1Pn-1)(a0E+

a1P+a2P2+…+an-1Pn-1)=BA，

所以矩阵AB也是结式循环矩阵，且AB=BA。

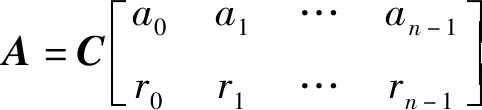
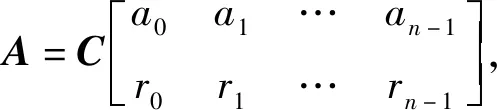
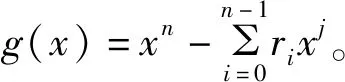
设ω0,ω1，…，ωn-1为g(x)=0的n个根，即矩阵P的n个特征值，记向量ni(i=0,1,…,n-1)是属于特征值ωi(i=0,1,…,n-1)的特征向量，

令Q=(n0，n1，…,nn-1)，

所以Q-1PQ=diag(ω0,ω1,…,ωn-1)。

由引理1.2得

A=f(P)=a0E+a1P+a2P2+…+an-1Pn-1，

则Q-1AQ=Q-1f(P)Q=a0Q-1Q+a1Q-1PQ

+a2Q-1P2Q+…+an-1Q-1Pn-1Q=

diag(f(ω0),f(ω1),…,f(ωn-1))，

即在复数域上存在可逆矩阵Q使得

B=Q-1AQ=

diag(f(ω0),f(ω1)，…，f(ωn-1))。

证明由性质2.5得矩阵

B=Q-1AQ=

diag(f(ω0),f(ω1)，…，f(ωn-1))，

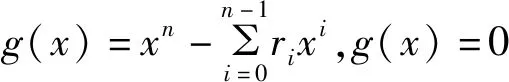
记矩阵Q=(n0,n1，…，nn-1)，其中向量ni(i=0，1，…，n-1)是属于特征值ωi的特征向量，

所以(Q-1AQ)-1=Q-1A-1Q=

diag(f-1(ω0)，f-1(ω1)，…，f-1(ωn-1))，

即A-1=h(P)=

l0E+l1P+l2P2+…+ln-1Pn-1。

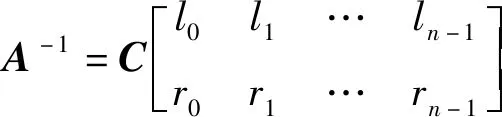
证明由性质2.5得矩阵

B=Q-1AQ=

diag(f(ω0)，f(ω1)，…，f(ωn-1))，

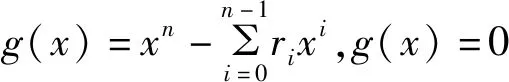
记矩阵Q=(n0,n1,…,nn-1)，其中向量ni(i=0，1，…，n-1)是属于特征值ωi的特征向量，

则(Q-1AQ)T=QTA-1(QT)-1=

(diag(f(ω0),f(ω1)，…，f(ωn-1)))T=

diag(f(ω0),f(ω1)，…，f(ωn-1))，

所以AT=

(Q-1)Tdiag(f(ω0),f(ω1)，…，f(ωn-1))QT，

由性质2.5得，存在可逆矩阵Q，使得

B=Q-1AQ=diag(f(ω0)，f(ω1)，…，f(ωn-1))，

即矩阵A与矩阵B相似，则有