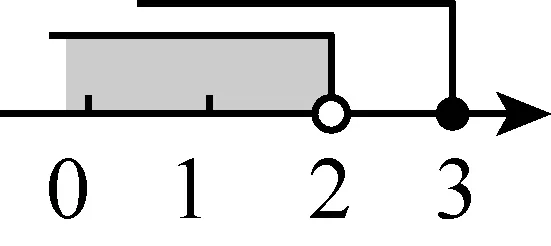
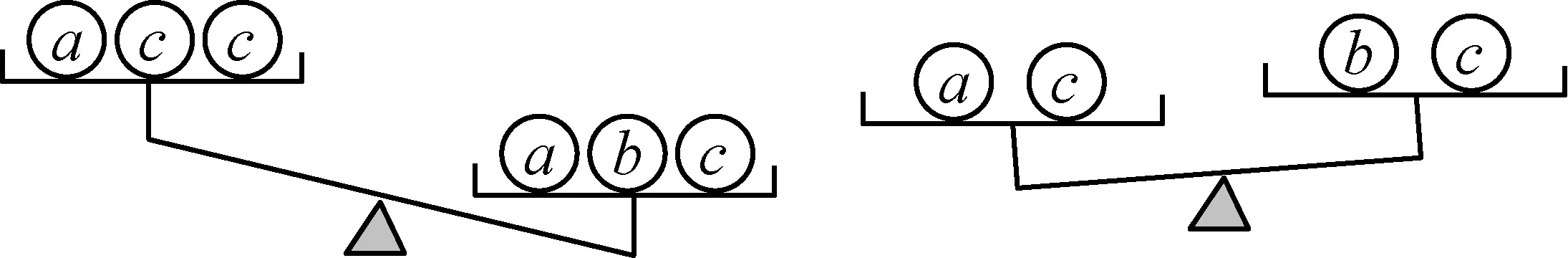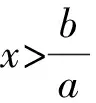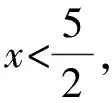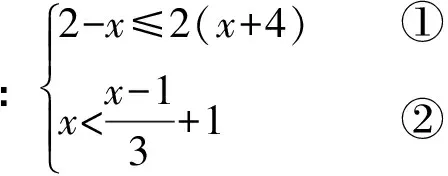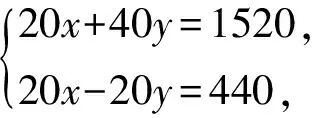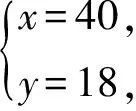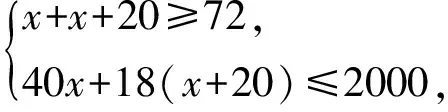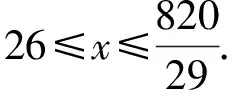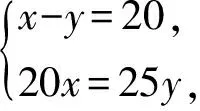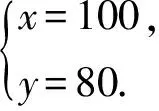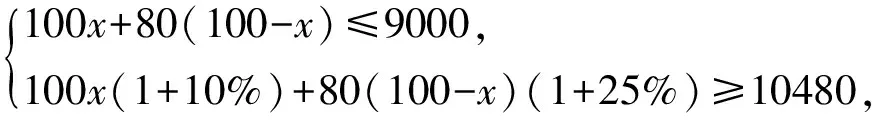关于不等式(组)在中考中的考点透视

2016-02-05李庆社

新课程教学(电子版) 2016年9期

关键词：文学名著数轴评析

李庆社

考点一：不等关系及不等式的性质

考点二：一元一次不等式(组)的解集

考点三：一元一次不等式(组)的解法

考点四：一元一次不等式(组)的应用

关于不等式(组)在中考中的考点透视

李庆社

(安徽省安庆市岳西县思源实验学校，岳西 246600)

本文就初中不等式(组)的知识在中考中常见的热点、考点以及考查力度、考查方式等进行了剖析，并以近年来各地中考题为例，分考点进行了详细说明，深度挖掘了解题中的数学思想方法，同时对今后不等式在中考中所考查的知识点和题型做出了预测，希望能对教师和学生关于这部分内容的复习有所帮助．

不等式中考考点知识链接考点预测

一元一次不等式与一元一次不等式组是初中数学的重要基础知识，在近几年的中考中，填空题、选择题、解答题均有涉及，分值占试卷总分值的8%左右．(1)不等式的基本性质、不等式解集的概念一般以选择题、填空题的形式进行考查，命题也比较基础；(2)解不等式(组)或不等式(组)的整数解的知识以选择题、填空题和解答题的方式考查，常常结合数轴，利用数形结合的思想来命题；(3)不等式(组)的应用题是近几年中考的热点，多以解答题出现，这类问题往往与一次函数、方程组等知识综合考查，命题难度也相对大一些．下面笔者就这部分的内容在近几年中考的考查情况进行逐一剖析．

考点一：不等关系及不等式的性质

基础知识链接：(1)列不等式，先设未知数再用代数式表示相关的量，通过寻找不等关系列不等式．审题时要注意抓住关键词，如“大于”“不超过”“不小于”等．(2)不等式的性质是解一元一次不等式(组)的主要依据．不等式的两边都乘(或除以)同一个负数，不等号的方向要改变．当不能明确不等式两边同乘(或除以)的是什么数时，就要进行分类讨论．

例1 (2015·湖南怀化)下列不等式变形正确的是

( )

A.由a>b得ac>bc

B.由a>b得-2a>-2b

C.由a>b得-a<-b

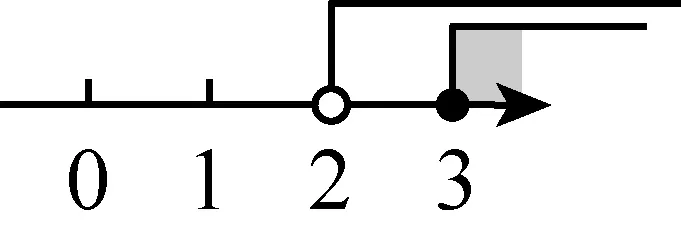
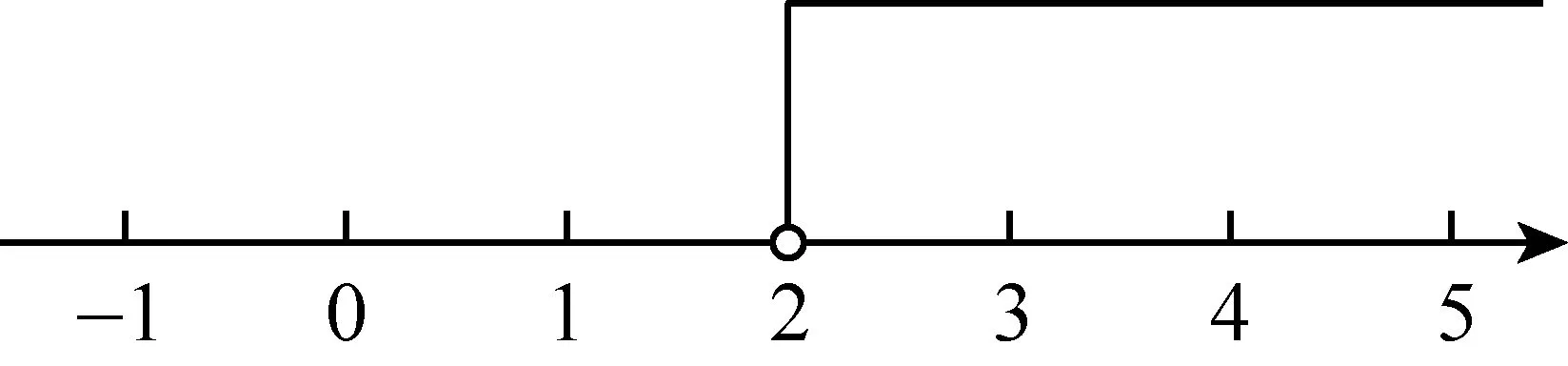
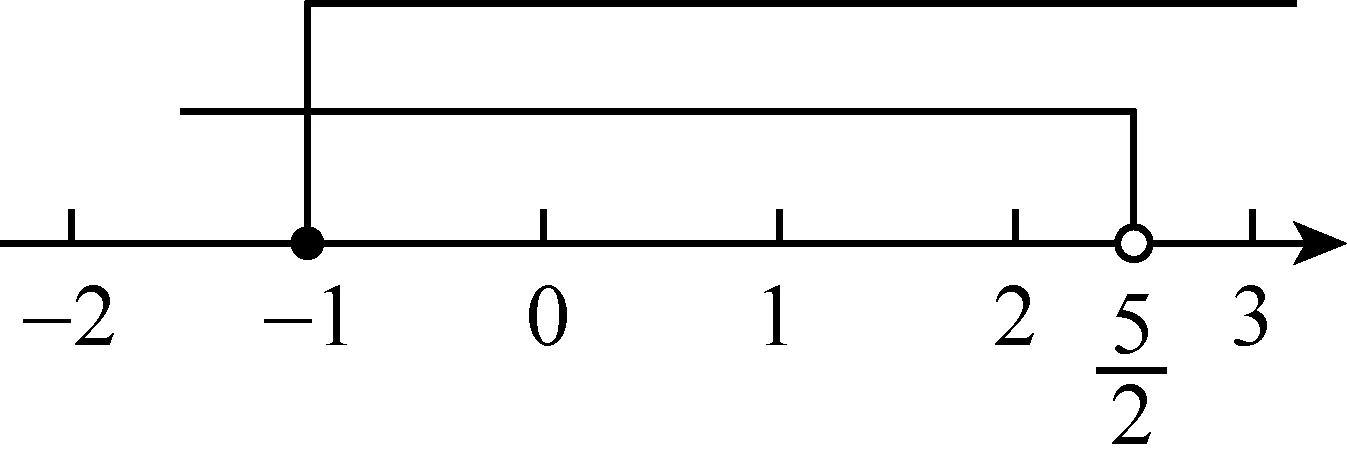
D.由a>b得a-2

解析：A.因为c的正负不确定，所以由a>b得ac>bc不正确，因为a>b，所以①c>0时，ac>bc；②c=0时，ac=bc；③c<0时，ac

B.不等式的两边同时乘(或除以)同一个负数，不等号的方向改变．因为a>b，所以-2a<-2b，则选项B不正确.

C.因为a>b，所以-a<-b，则选项C正确.

D.不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子，不等号的方向不变．因为a>b，所以a-2>b-2，则选项D不正确．故选C．

评析：此题主要考查了不等式的基本性质.(1)不等式的两边同时乘(或除以)同一个正数，不等号的方向不变；(2)不等式的两边同时乘(或除以)同一个负数，不等号的方向改变；(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子，不等号的方向不变．

( )

(1) (2)图1

解析：注意到a+c>b+c,所以a>b．又根据图1(1)知b>c，故a>b>c．选A正确．

评析：灵活运用不等式的基本性质，先将三种物体转化为数量关系，再进行大小比较，是本题解题的关键．

考点预测：中考题主要考查用不等式表示常见的不等关系，题型主要以填空题、选择题为主，更多的是将不等式渗透到其他数学知识中进行考查．另外，从实际生活中归纳不等式模型[1]是今后中考的热点．

考点二：一元一次不等式(组)的解集

基础知识链接：(1)使不等式(组)成立的未知数的取值范围是不等式的解集．(2)明确不等式的解与解集的区别．用数轴表示不等式解集时，要抓住两点：一是定边界点，注意点是实心还是空心；二是定方向．

例3 (2016 ·甘肃平凉)在数轴上表示不等式x-1<0的解集，正确的是

( )

解析：解不等式x-1<0得x<1，故选C．

(1) 用不等式表示：一般地，一个含未知数的不等式有无数个解，其解集是一个范围，这个范围可用最简单的不等式表达出来，例如x-1≤2的解集是x≤3．

(2) 用数轴表示：不等式的解集可以在数轴上直观地表示出来，形象地说明不等式有无限多个解，用数轴表示不等式的解集要注意一是定边界点，二是定方向[2]．

(3)能使不等式成立的未知数的值，叫作不等式的解．

( )

解析：分别求出每一个不等式的解集，根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则即可得答案．解不等式2x-1≥5，得x≥3,解不等式8-4x<0，得x>2，故不等式组的解集为x≥3．故选C．

评析：不等式组解集在数轴上的表示方法：把每个不等式的解集在数轴上表示出来(>，≥向右画；<，≤向左画)，数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”“≤”要用实心圆点表示；“<”“>”要用空心圆点表示．

( )

A.m≥1 B.m≤1 C.m≥0 D.m≤0

评析：此题考查了不等式的解集，熟练掌握不等式组取解集的方法是解本题的关键．

考点预测：不等式或不等式组的解集常常与数轴紧密联系在一起，考查的要点主要是给出不等式(组)的解集，用数轴表示出来，运用数形结合思想进行分析．

考点三：一元一次不等式(组)的解法

基础知识链接：在学习一元一次不等式的解法时，对比一元一次方程的解法，会降低难度，只是在系数化为1时，如果系数是负数，应注意不等号的方向要改变．解一元一次不等式组，首先求出每个不等式的解集，标在同一个数轴上，其公共部分即为不等式的解集，没有公共部分的可视为无解．

解析：先去分母、再去括号、移项、合并同类项、系数化为1即可求出此不等式的解集，再在数轴上表示出其解集即可．

解：去分母，得 1+x<3x-3，

移项，得x-3x<-3-1，

合并同类项，得 -2x<-4，

系数化为1，得x>2，

将解集表示在数轴上如图3所示．

图3

评析：本题考查了解一元一次不等式，在数轴上表示不等式的解集的应用，解答本题的关键是熟练掌握解不等式的方法步骤．

解一元一次不等式与解一元一次方程的方法步骤类似，只是在利用不等式基本性质3对不等式进行变形时，要改变不等式的符号．

有两种解题思路：

(1)可以利用不等式的基本性质，设法将未知数保留在不等式的一边，其他项在另一边；

(2)采用解一元一次方程的解题步骤，即去分母、去括号、移项、合并同类项、系数化为1等．

解析：分别求出每一个不等式的解集，根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则在数轴上将解集表示出来．

解不等式3(x+2)≥x+4，得x≥-1，

将不等式解集表示在数轴上如图4所示．

图4

评析：本题考查的是解一元一次不等式组，正确求出不等式解集是解题的基础，熟知“同大取大，同小取小，大小小大中间找，大大小小找不到”的原则是解答此类问题的关键．

解不等式①，得x≥-2，

解不等式②，得x<1，

则不等式组的解集为-2≤x<1．

所以不等式组的最大整数解为x=0．

评析：此题考查了解一元一次不等式组，以及一元一次不等式组的整数解，熟练掌握运算法则是解答本题的关键．

考点预测：把握解不等式的主线，有意识地领会、感悟隐含在知识中的数学思想方法，并灵活运用数学思想方法巧妙解题．

考点四：一元一次不等式(组)的应用

基础知识链接：运用一元一次不等式(组)解决实际问题，要认真阅读题目，正确理解题意，高度抽象概括，寻找等量关系，建立数学模型，解决实际问题．注意统筹安排、合理决策．解决实际问题时还要考虑到解的取值应符合实际情况．

例9 (2015·广西桂林)“全民阅读”深入人心，好读书，读好书，让人终身受益．为满足同学们的读书需求，学校图书馆准备到新华书店采购文学名著和动漫书两类图书．经了解，20本文学名著和40本动漫书共需1520元，20本文学名著比20本动漫书多440元(注：所采购的文学名著价格都一样，所采购的动漫书价格都一样)．

(1)求每本文学名著和动漫书各多少元．

(2)若学校要求购买动漫书比文学名著多20本，动漫书和文学名著总数不低于72本，总费用不超过2000元，求出所有符合条件的购书方案．

解析：(1)设每本文学名著x元，动漫书y元，根据题意列出方程组解答即可；(2)根据学校要求购买动漫书比文学名著多20本，动漫书和文学名著总数不低于72本，总费用不超过2000元，列出不等式组，解答即可．

解：(1)设每本文学名著x元，动漫书y元，

答：每本文学名著为40元，每本动漫书为18元．

(2)设学校要求购买文学名著x本，动漫书为(x+20)本，根据题意可得

根据题意x的值需要取整数，

所以x取26，27，28．

方案一：文学名著26本，动漫书46本；

方案二：文学名著27本，动漫书47本；

方案三：文学名著28本，动漫书48本．

评析：本题将二元一次方程组、一元一次不等式组的运用综合起来考查．读懂题意，根据题意列式，再根据题意的实际情况正确求解，方可解决问题．

例10 (2016·湖南湘西)某商店购进甲、乙两种商品，甲的进货单价比乙的进货单价高20元，已知20个甲商品的进货总价与25个乙商品的进货总价相同．

(1)求甲、乙每个商品的进货单价；

(2)若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于9000元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于10480元，问有哪几种进货方案．

(3)在条件(2)下，并且不再考虑其他因素，若甲、乙两种商品全部售完，哪种方案利润最大？最大利润是多少？

解析：(1)设甲商品的进货单价是x元，乙商品的进货单价是y元，根据甲的进货单价比乙的进货单价高20元，已知20个甲商品的进货总价与25个乙商品的进货总价相同即可列方程组求解；(2)设甲进货x件，乙进货(100-x)件，根据两种商品的进货总价不高于9000元，两种商品全部售完后的销售总额不低于10480元即可列不等式组求解；(3)将销售利润用甲进货的数量的函数来表示，利用函数的性质即可求解．

解：(1)设甲商品的进货单价是x元，乙商品的进货单价是y元．