如何求向量的夹角
2018-06-04李怡洁
中学生数理化·高一版 2018年5期
■李怡洁
两个向量的夹角是指当两个向量的起点相同时,表示这两个向量的有向线段所形成的角。若起点不同,应先通过平移,使其起点相同,再观察夹角。两个向量夹角的范围为[0,π],特别地,当两个向量共线且同向时,其夹角为0,共线且反向时,其夹角为π。
向量的夹角与向量所在直线所成的角不同,前者的范围是[0,π],而后者的范围是
题型1:通过向量的运算获取模长与向量的数量积,求向量的夹角
例 1已知|a|=2,|b|=1,a与b的夹角为60°,求向量m=2a+b与向量n=a-4b的夹角θ的余弦值。
解:由题意知a·b=2×1×cos 60°=1。
|m|2=2a+b2=4|a|2+4a·b+|b|2=4×22+4×1+1=21。
|n|2=a-4b2=|a|2-8a·b+16|b|2=22-8×1+16×1=12。
由上可得|m|=21,|n|=23。
又因为m·n=(2a+b)·(a-4b)=2|a|2-7a·b-4|b|2=2×22-7×1-4×1=-3,
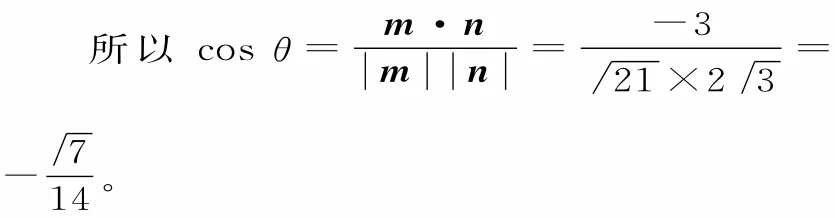
解答本题先通过题设条件,利用向量的运算确定|m|2,|n|2,m·n的值,然后求其夹角。
题型2:通过向量的运算获取模长与向量数量积的关系,求向量的夹角
例2若非零向量a,b满足|a|=3|b|=|a+2b|,求a与b夹角的余弦值。
解:由|a|=|a+2b|,两边平方得|a|2=|a|2+4a·b+4|b|2,得a·b=-b2,所以
先通过题设条件,利用向量的运算得到a·b=-b2=-b2,然后求其夹角。
题型3:通过向量的运算获取向量的模长与模长的关系,求向量的夹角
例 3已知a与b是两个非零向量,且|a|=|b|=|a+b|,求向量b与向量a-b的夹角。
解:设向量b与向量a-b的夹角为θ。
因为|b|=|a+b|,|b|=|a|,所以b2=(a+b)2,即|b|2=|a|2+2a·b+|b|2,可得a·b=-

利用题设条件得到|ab|=|b|是解答本题的关键。本题也可利用数形结合的方法,借助图形直接求解。
