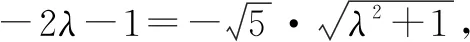把脉向量中两类夹角背景下参数的取值范围问题

蔡勇全

(四川省资阳市外国语实验学校 641300)

在平面内,非零向量a，b的夹角为锐(钝)角的背景下探求参数的取值范围是一类典型的易错易混问题，常见错误是将a，b的夹角为锐(钝)角与a·b>0(<0)混为一谈.事实上，二者并不等效.一方面，若a，b的夹角为锐(钝)角，则一定有a·b>0(<0)；另一方面，若a·b>0(<0)，则其原因还可能是a，b的夹角为0°(180°).因此，a·b>0(<0)是a，b的夹角为锐(钝)角的必要不充分条件，a·b>0(<0)与a，b的夹角所在的范围是[0°，90°)((90°，180°])才是等价关系.从而当a，b的夹角为锐(钝)角时,参数的取值范围应该是从a·b>0(<0)时参数的取值范围中排除a，b的夹角为0°(180°)时参数的具体值后余下的部分.本文结合实例，谈谈在两向量的夹角为锐(钝)角的背景下参数的取值范围的求解策略，供大家参考.

一、夹角为锐角

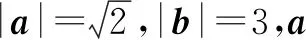
解析若(a+λb)·(λa+b)>0，即得λa2+(λ2+1)(a·b)+λb2>0.所以λ|a|2+(λ2+1)|a||b|cos45°+λ|b|2>0.即3λ2+11λ+3>0.

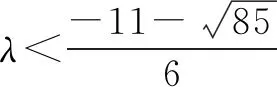
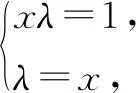
解得λ=1或λ=-1(舍去).

综上，当向量a+λb与λa+b的夹角为锐角时，实数λ的取值范围是(-，(1，+).

变式1已知向量m=(-2，3)，n=(1，t)，若向量m+n与m-n的夹角为锐角，求实数t的取值范围.

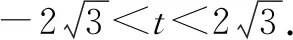
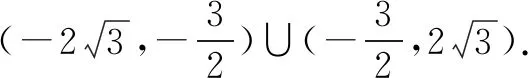
变式2已知△ABC的顶点坐标分别为A(3，4)，B(0，0)，C(c，0).

(1)若c=5，求sinA的值；

(2)若∠A是锐角，求c的取值范围.

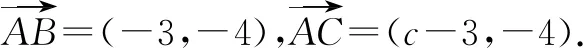
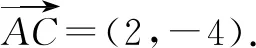
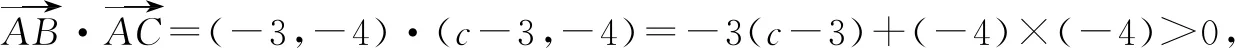
评注例1及其变式1，2的解答结果清楚地说明，如果不将两向量夹角为0°时，参数的具体值从两向量的数量积大于0时参数的取值范围中剔除，那么极有可能会出现增解.另外，解决上述例1，如果直接从向量a+λb与λa+b的夹角为锐角出发列式，那么应该解答如下:

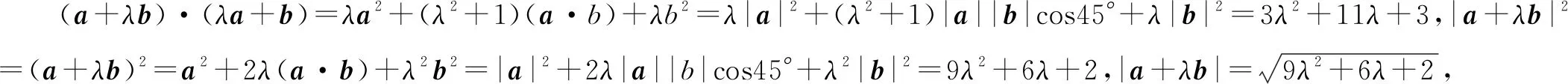
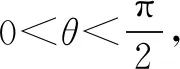
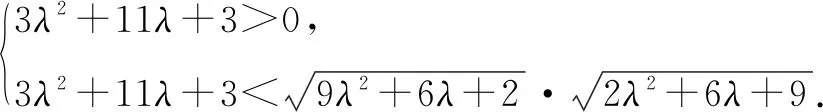
解得实数λ的取值范围是(-，(1，+).相比之下，这种思路比前一种做法更加清晰简单，但比前一种做法的运算量就大得多.因此，数学解题既是探索各种解答方法的过程，也是选择运算量多少的过程.

二、夹角为钝角

例2 已知向量a=(-2，-1)，b=(λ，1)，且a与b的夹角为钝角，求实数λ的取值范围.

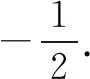
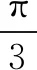
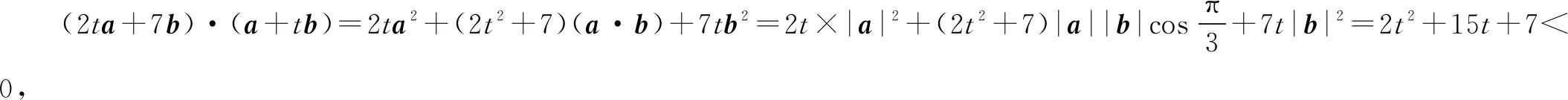
变式2设向量a=(m-2，m+3)，b=(2m+1，m-2)，若a与b的夹角大于90°，求实数m的取值范围.